ANGLES Learning objectives 1 Sum of angles at

ANGLES Learning objectives 1. Sum of angles at a point 2. Angles on a straight line 3. Angles in a triangle; 4. Angles in a quadrilateral 5. Vertically opposite angles

STARTER Which shape(s) has. . . BRAVE A. 4 sides B. 3 sides C. 6 square faces D. 4 right angles and 2 longer sides E. 5 sides F. 6 sides

Thursday, December 23, 2021 Lesson 1: ANGLES Learning Objective: To identify 3 types of angles and estimate size of angles. Learning outcomes: LO: To calculate the unknown angles

Class discussion What do we know about angles? • Where can we see angles in everyday life? They are not ANGELS
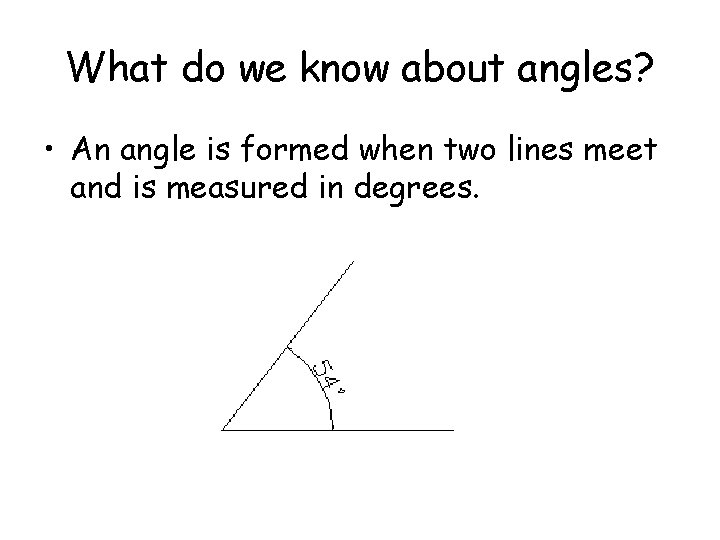
What do we know about angles? • An angle is formed when two lines meet and is measured in degrees.

What do we know about angles? • An angle is formed when two lines meet and is measured in degrees. • We use a little circle ° following the number to mean degrees. • For example 54° means 54 degrees
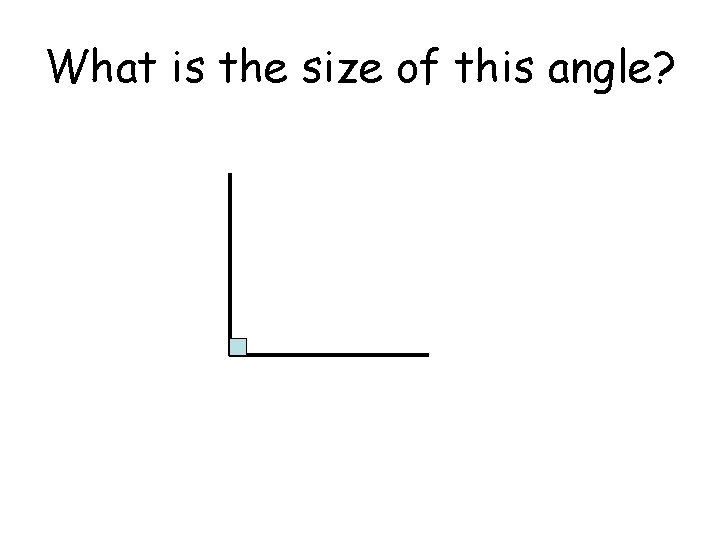
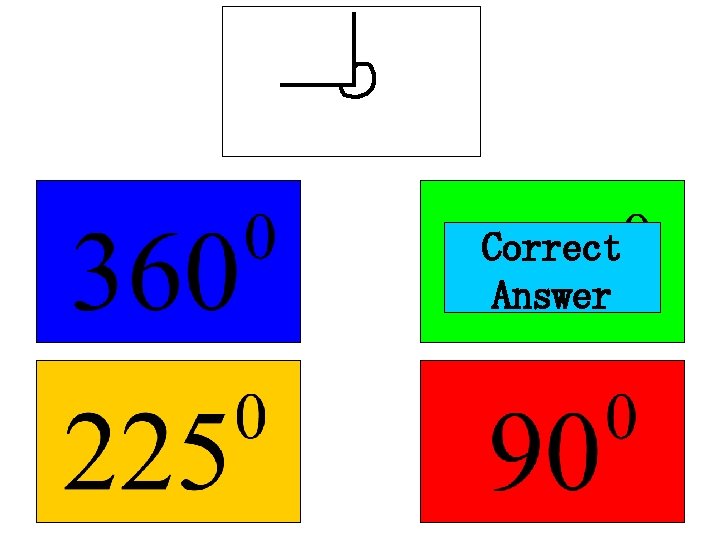
What is the size of this angle?
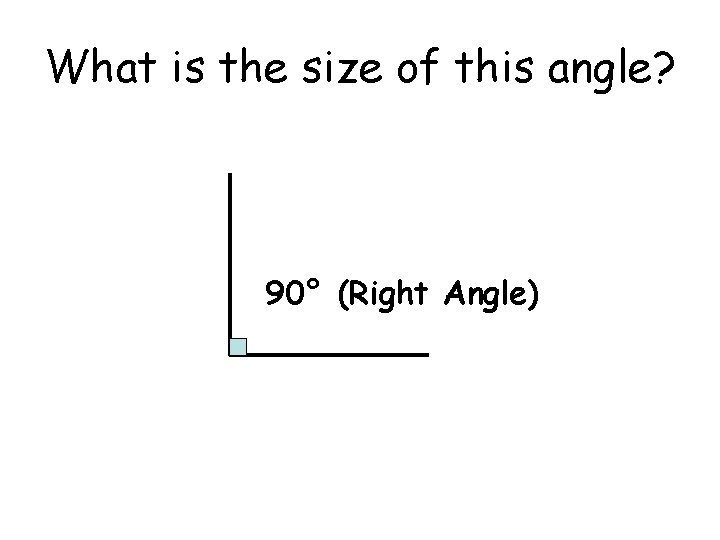
What is the size of this angle? 90° (Right Angle)
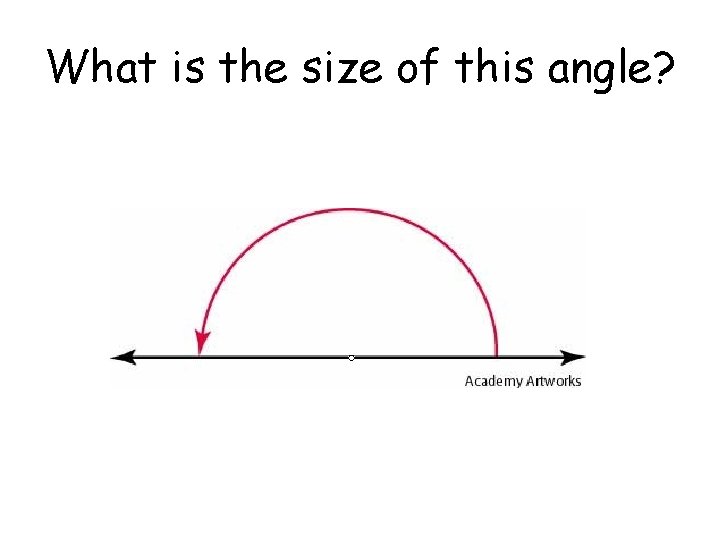
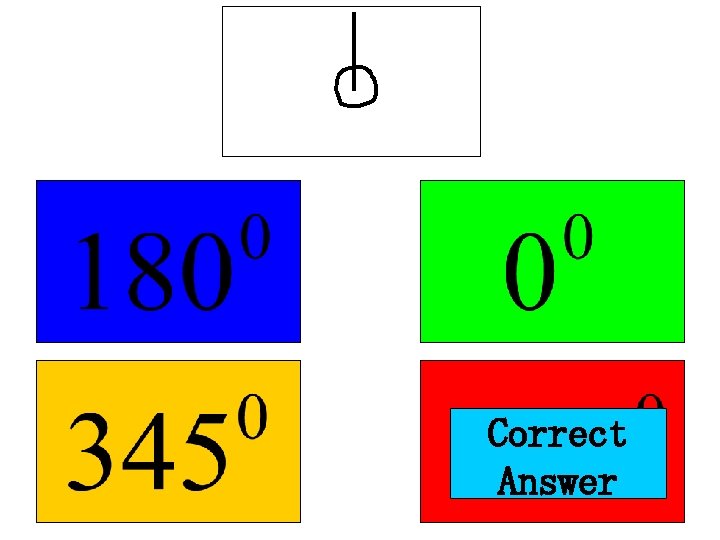
What is the size of this angle?
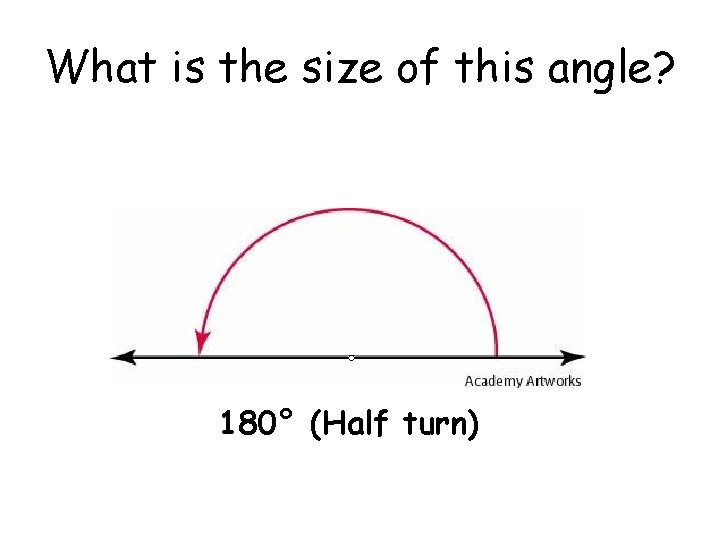
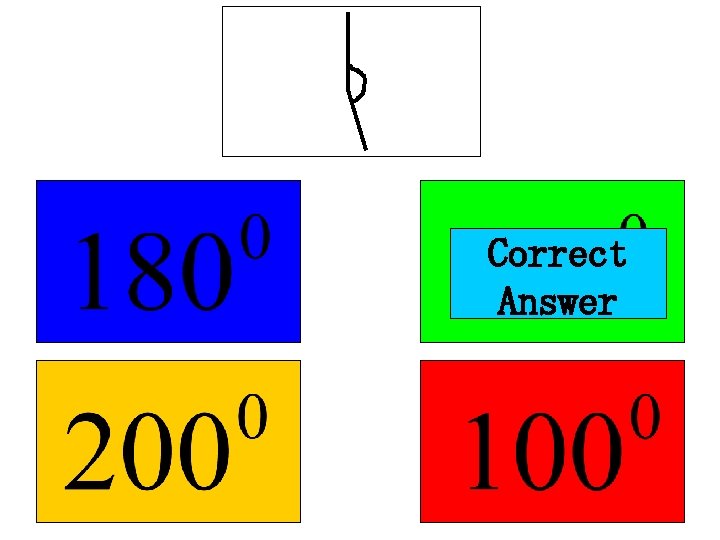
What is the size of this angle? 180° (Half turn)
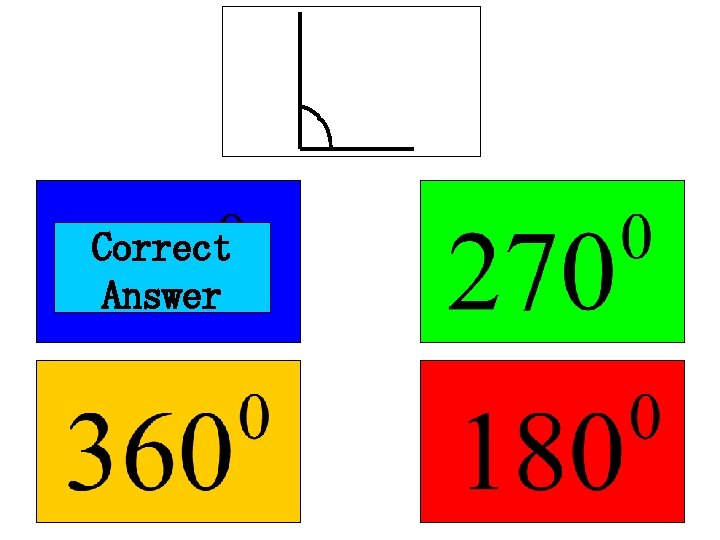
What is the size of this angle?
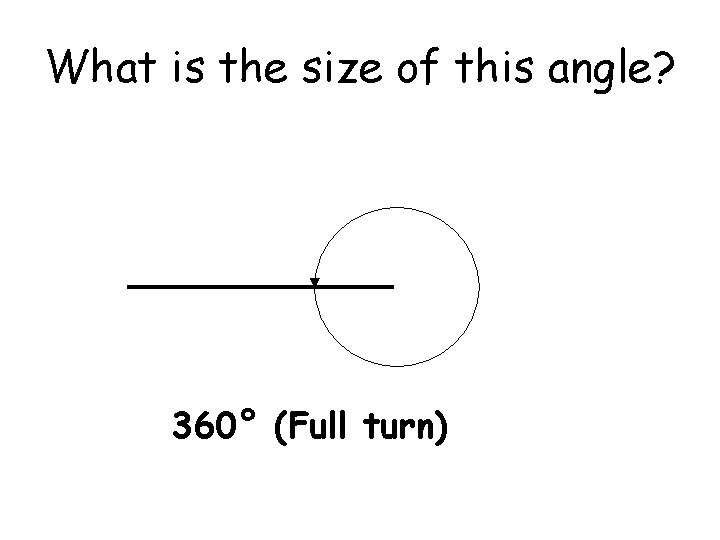
What is the size of this angle? 360° (Full turn)
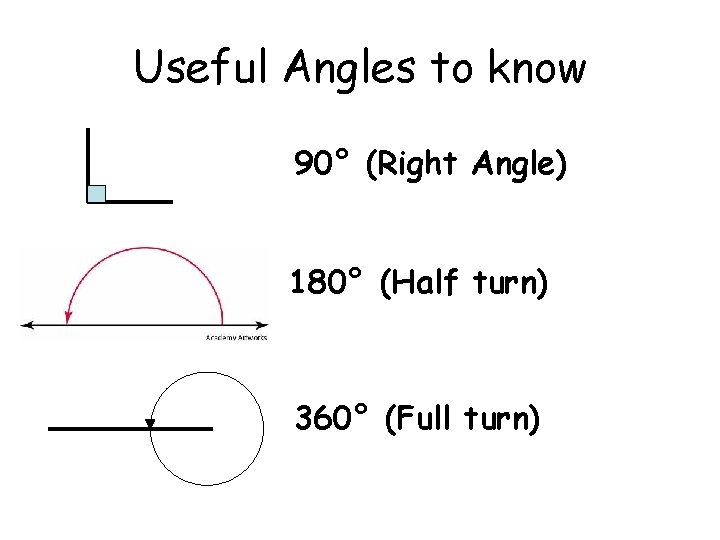
Useful Angles to know 90° (Right Angle) 180° (Half turn) 360° (Full turn)
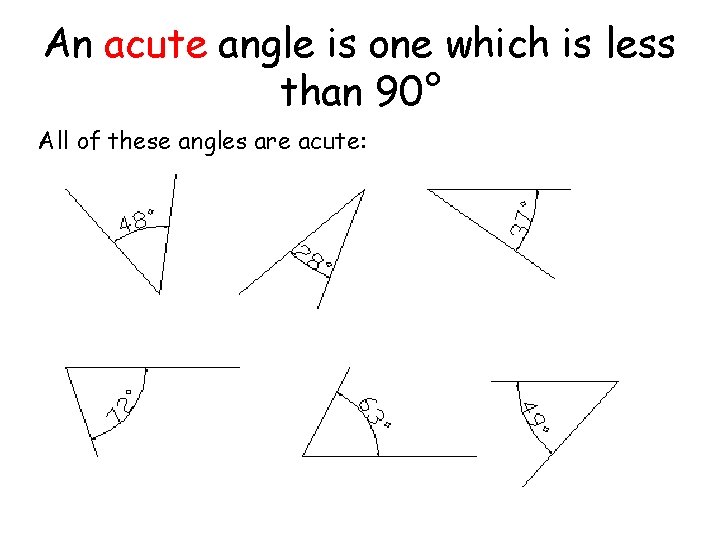
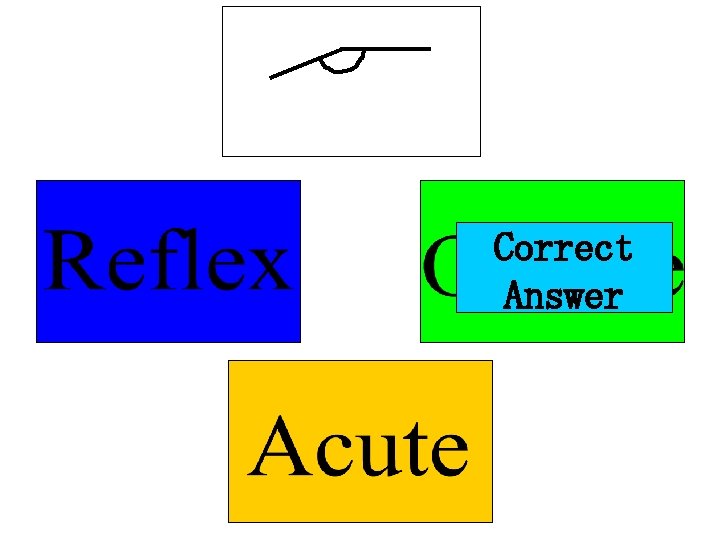
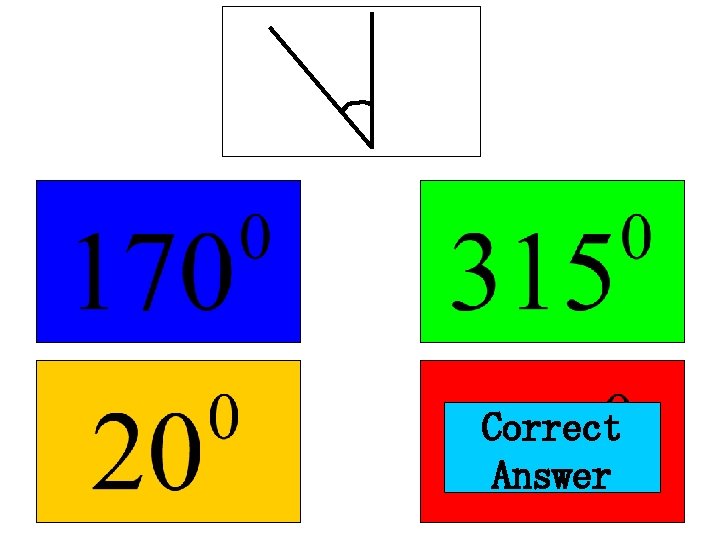
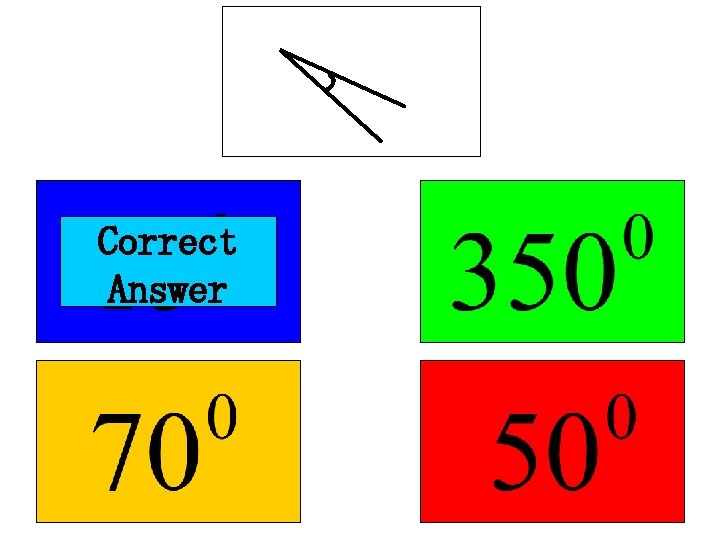
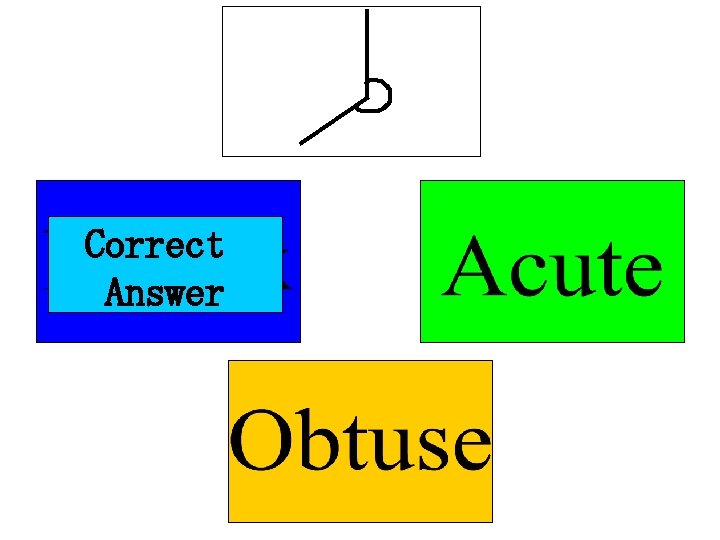
An acute angle is one which is less than 90° All of these angles are acute:
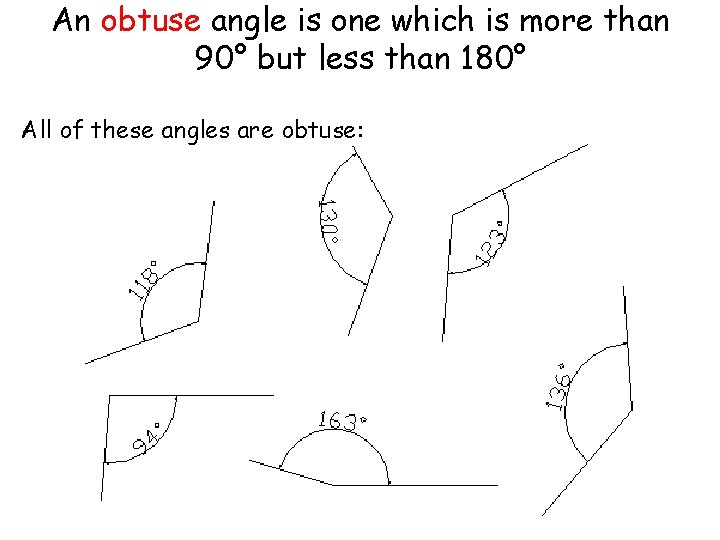
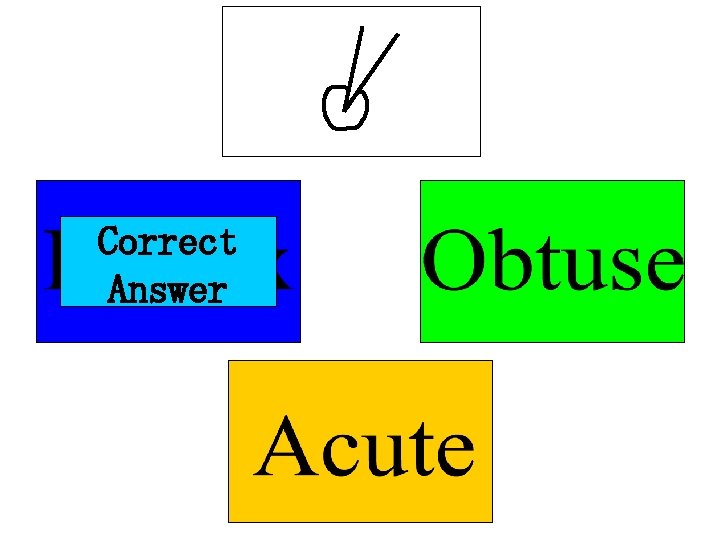
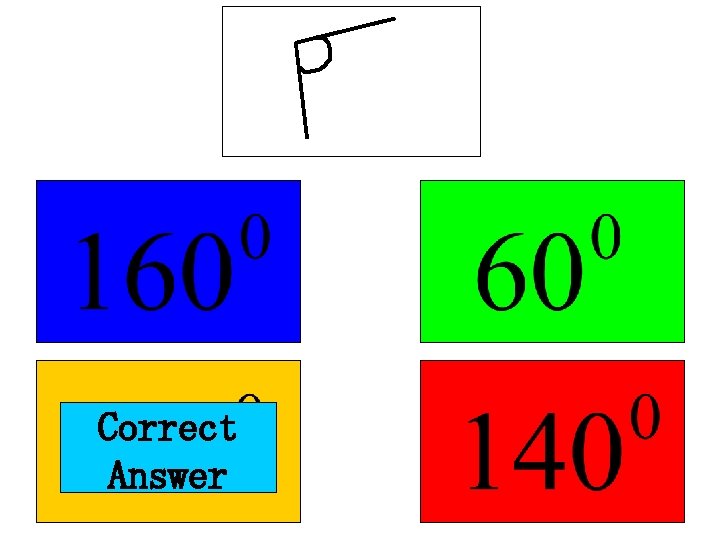
An obtuse angle is one which is more than 90° but less than 180° All of these angles are obtuse:
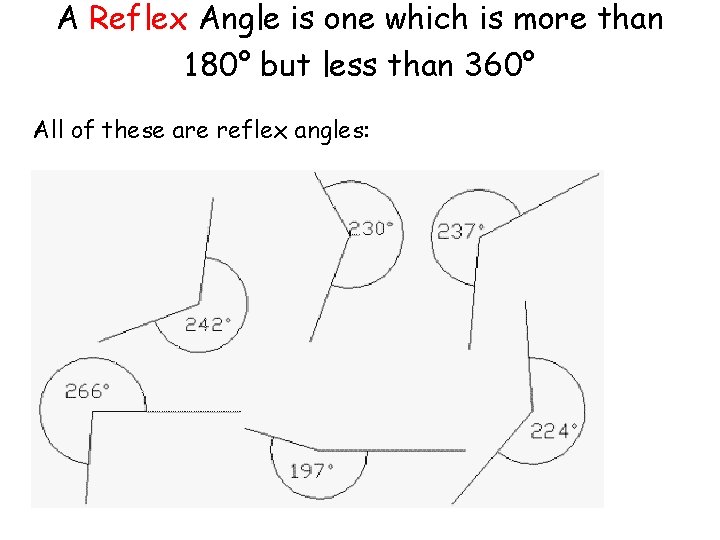
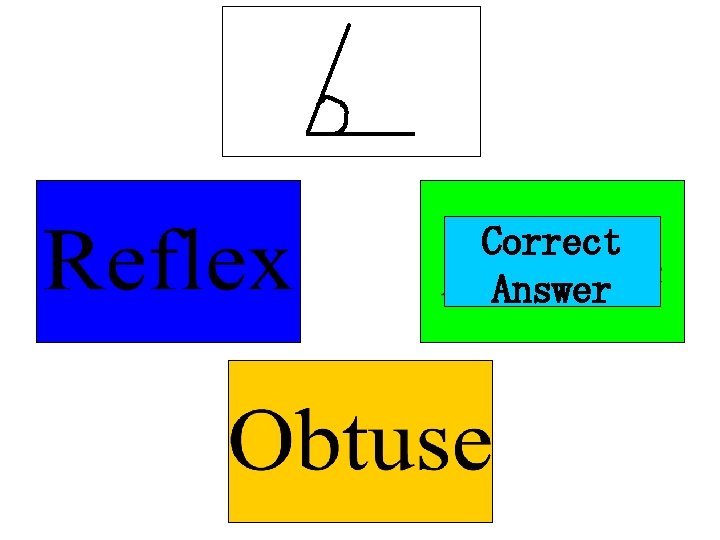
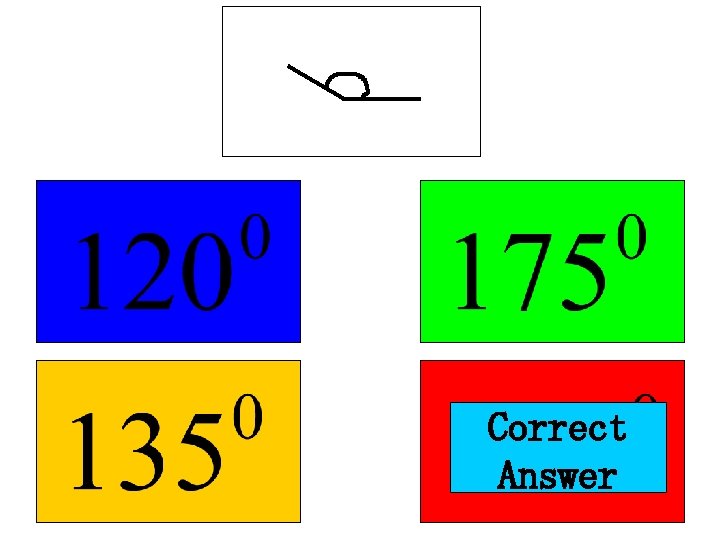
A Reflex Angle is one which is more than 180° but less than 360° All of these are reflex angles:

Summary • Acute Angle: less than 90° • Obtuse Angle: more than 90° but less than 180° • Reflex Angle: more than 180° but less than 360°
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
Correct Answer
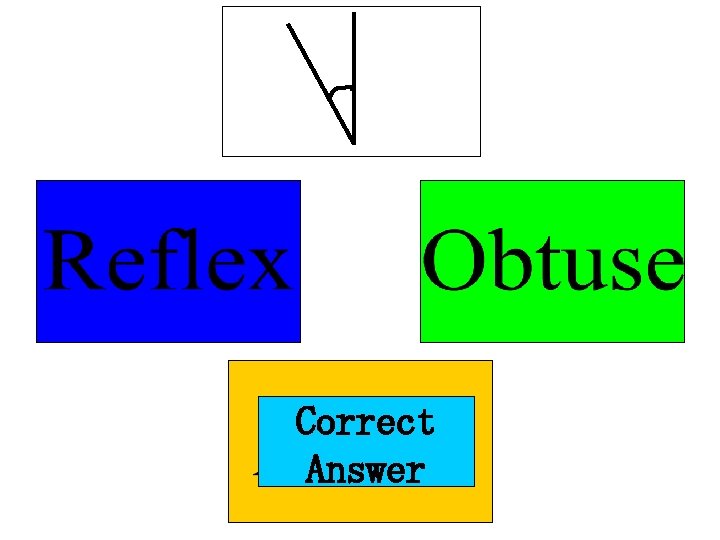
Correct Answer

WISH:
Angles in a triangle

Angles on a straight line
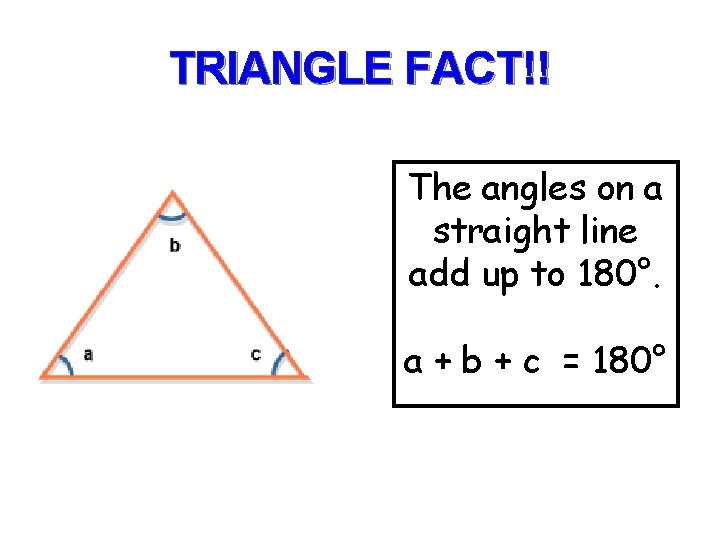
TRIANGLE FACT!! The angles on a straight line add up to 180°. a + b + c = 180°
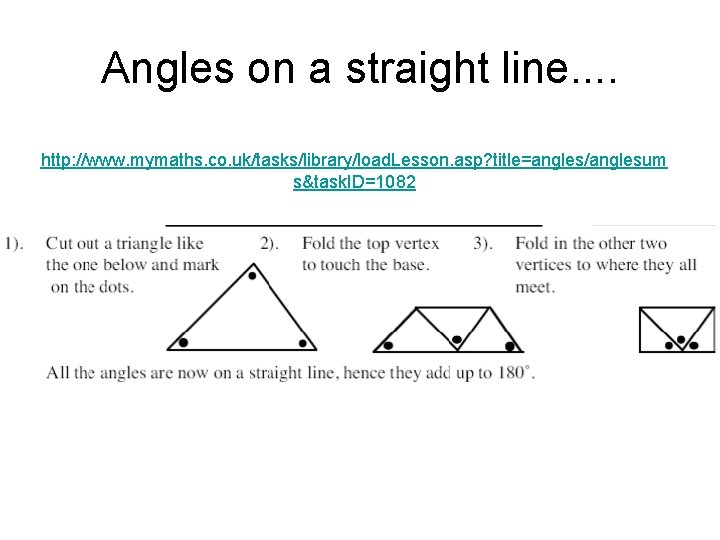
Angles on a straight line. . http: //www. mymaths. co. uk/tasks/library/load. Lesson. asp? title=angles/anglesum s&task. ID=1082
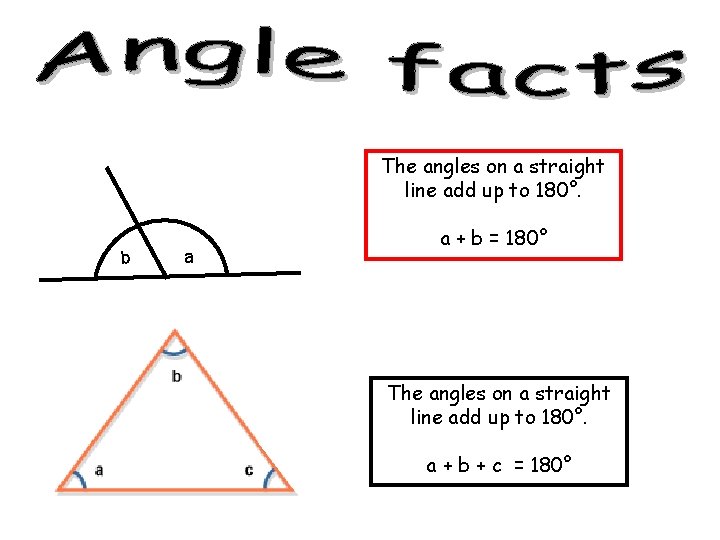
The angles on a straight line add up to 180°. b a a + b = 180° The angles on a straight line add up to 180°. a + b + c = 180°
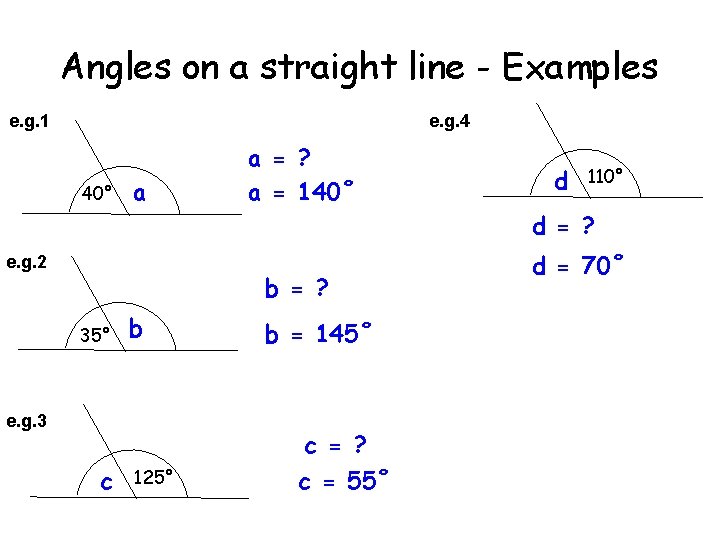
Angles on a straight line - Examples e. g. 1 e. g. 4 40° a a = ? a = 140˚ d 110° d = ? e. g. 2 b = ? 35° b e. g. 3 b = 145˚ c = ? c 125° c = 55˚ d = 70˚
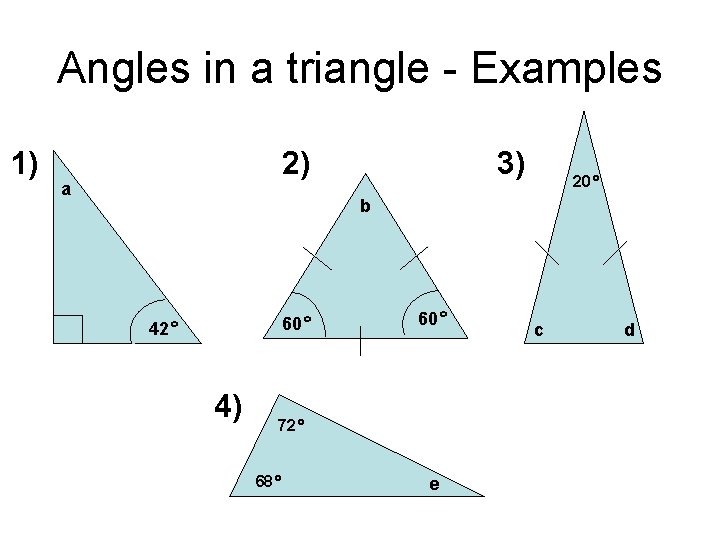
Angles in a triangle - Examples 1) 3) 2) a 20° b 60° 42° 4) 60° 72° 68° e c d

Thursday th 9 July 2020 Can you unjumble the words to find out the maths word? 1. rtngleai 4. qeuasr 2. trotorapcr 5. adrirallatque 3. Nglae 6. esreedg

Starter: MATHANAGRAMS Can you unjumble the words to find out the maths word? 1. triangle 4. square 2. protractor 5. quadrilateral 3. angle 6. degrees
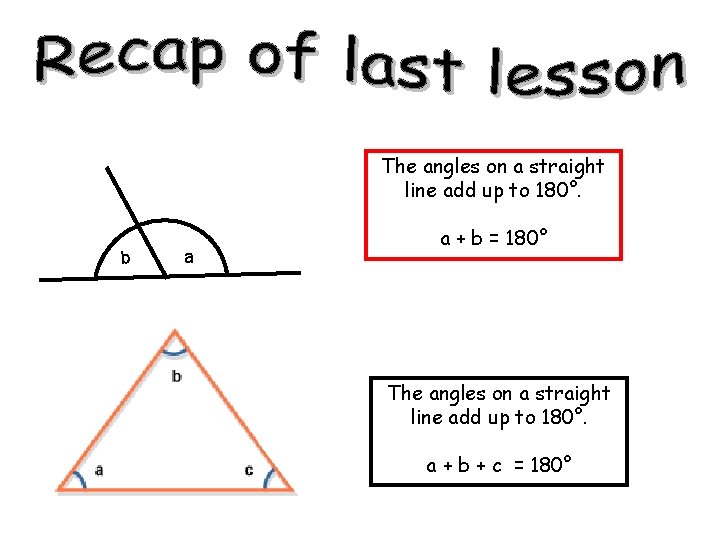
The angles on a straight line add up to 180°. b a a + b = 180° The angles on a straight line add up to 180°. a + b + c = 180°
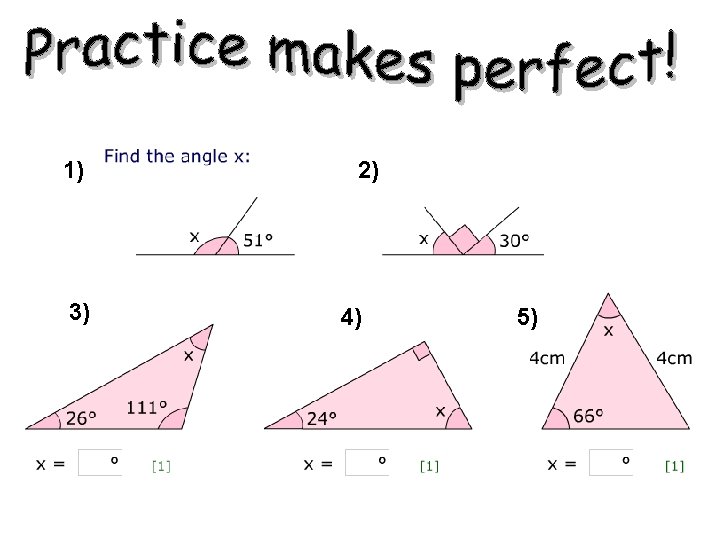
1) 4) 3) 2) 5) 4) 5) 6)

Thursday, December 23, 2021 ANGLES Learning Objective: To calculate unknown angles around a point and in a quadrilateral and vertically opposite angles.

Angles around a point
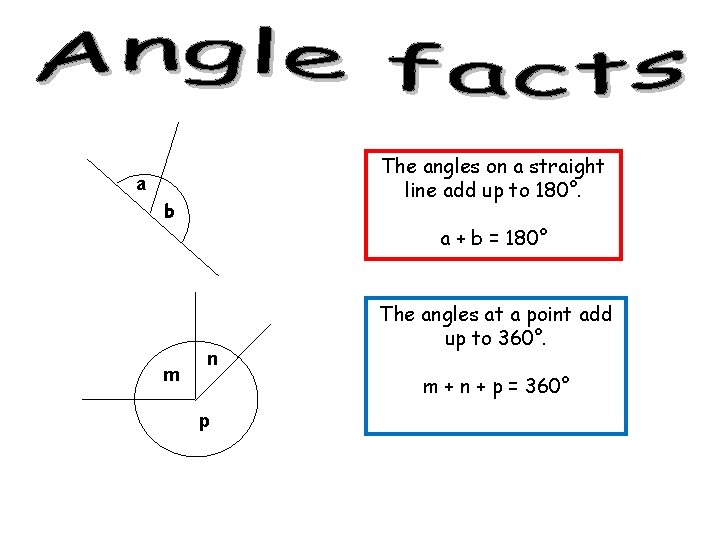
The angles on a straight line add up to 180°. a b a + b = 180° m n The angles at a point add up to 360°. m + n + p = 360° p
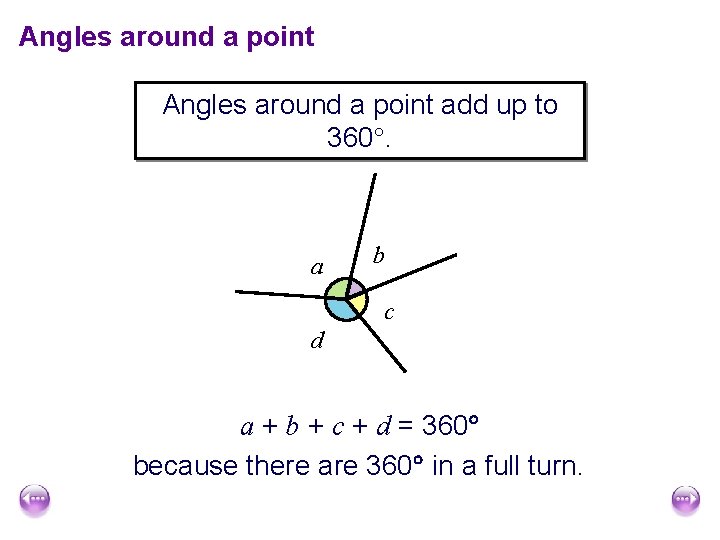
Angles around a point add up to 360. a b c d a + b + c + d = 360 because there are 360 in a full turn.
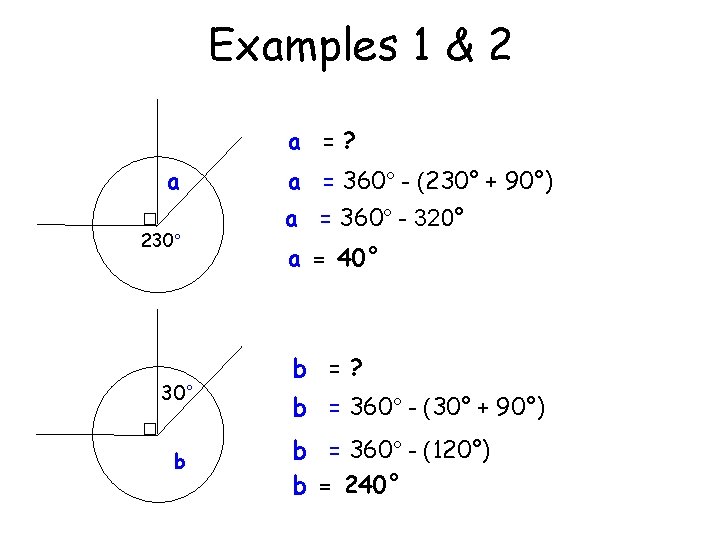
Examples 1 & 2 a =? a 230° b a = 360° - (230° + 90°) a = 360° - 320° a = 40° b =? b = 360° - (30° + 90°) b = 360° - (120°) b = 240°
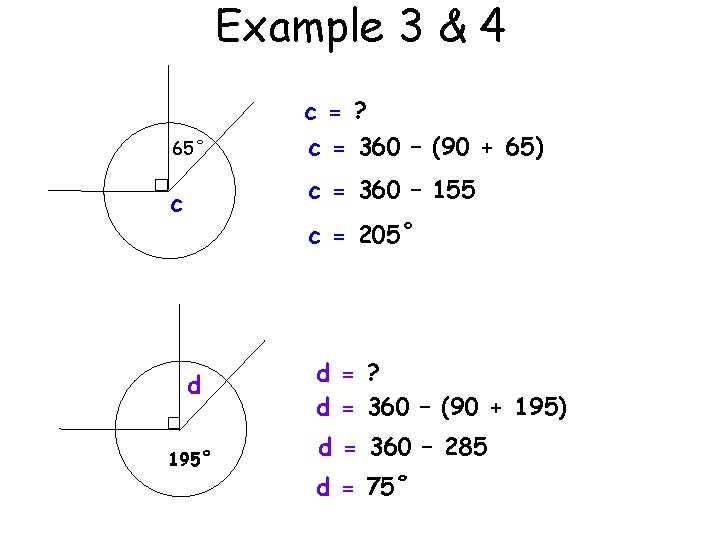
Example 3 & 4 c = ? 65˚ c = 360 – (90 + 65) c = 360 – 155 c c = 205˚ d 195˚ d = ? d = 360 – (90 + 195) d = 360 – 285 d = 75˚
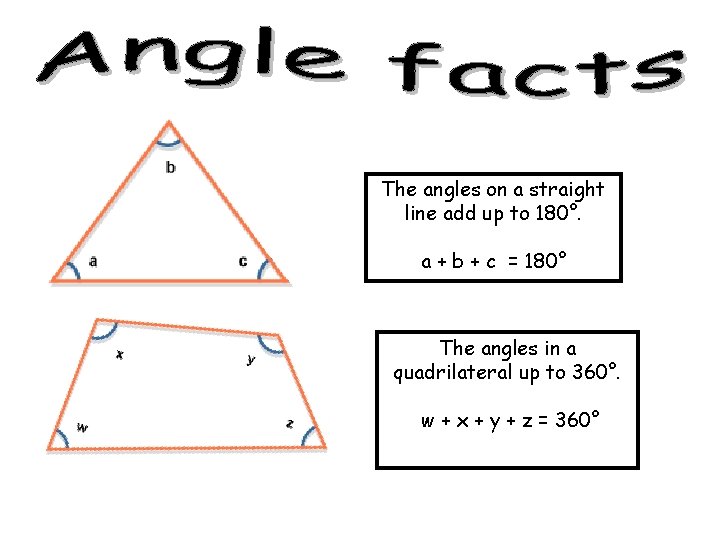
The angles on a straight line add up to 180°. a + b + c = 180° The angles in a quadrilateral up to 360°. w + x + y + z = 360°
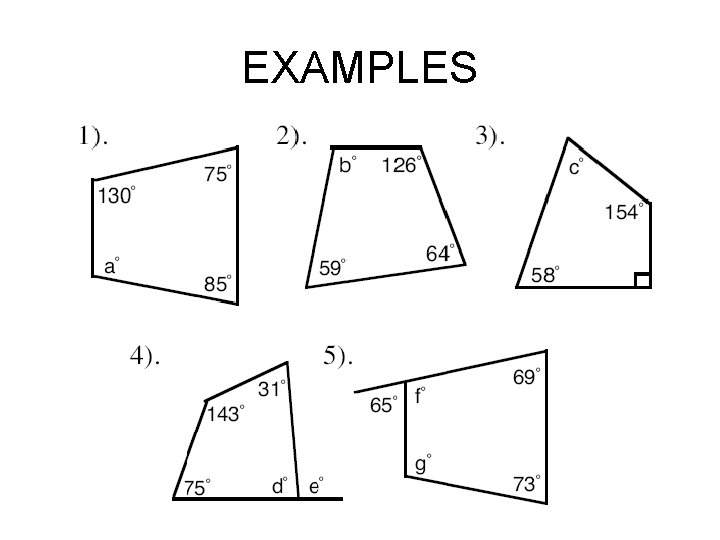
EXAMPLES
Intersecting lines
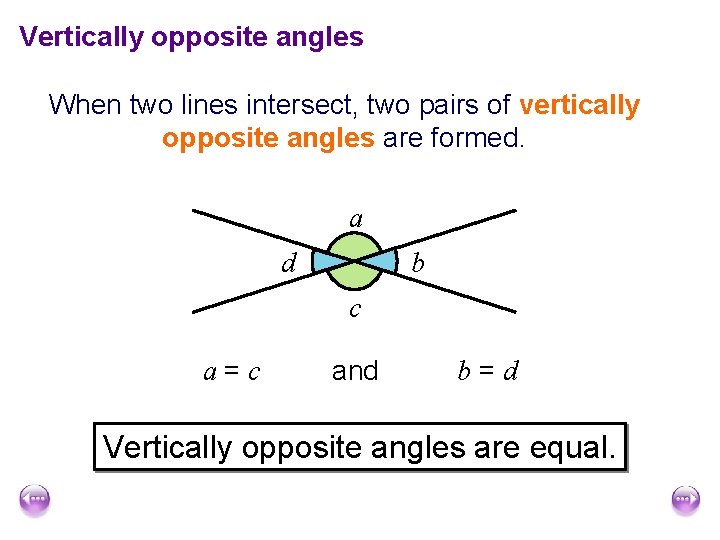
Vertically opposite angles When two lines intersect, two pairs of vertically opposite angles are formed. a d b c a=c and b=d Vertically opposite angles are equal.
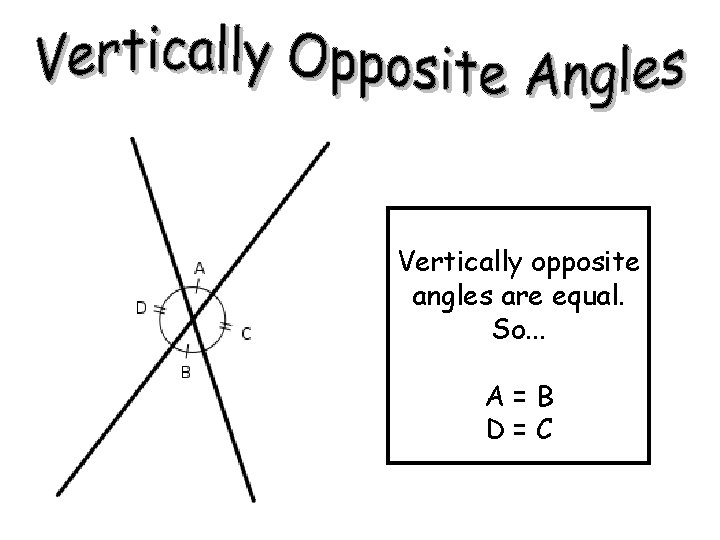
Vertically opposite angles are equal. So. . . A=B D=C
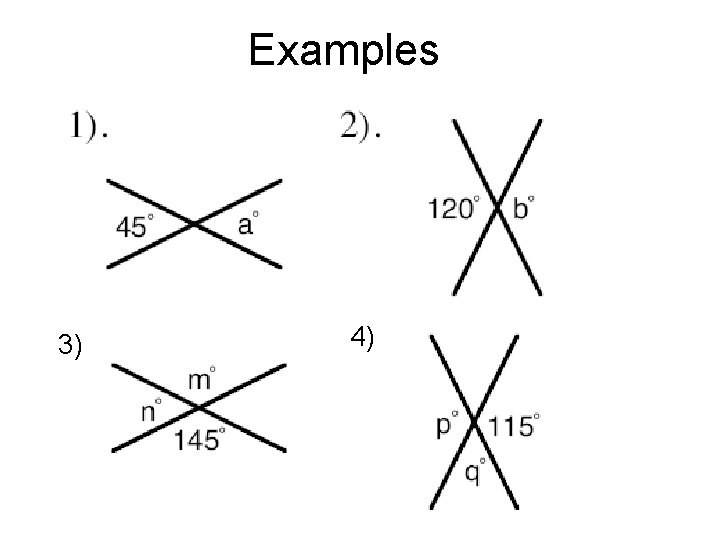
Examples 3) 4)

True or False? The sum of all the angles around a point is. . . 360˚ The sum of all the angles on a straight line is. . . 130˚ The sum of angles in a triangle is. . . 120˚

True or False? The sum of all the angles around a point is. . . 360˚ TRUE : D The sum of all the angles on a straight line is. . . 130˚ FALSE correct answer is 180˚ The sum of angles in a triangle is. . . 120˚ FALSE correct answer is 180˚

WISH:
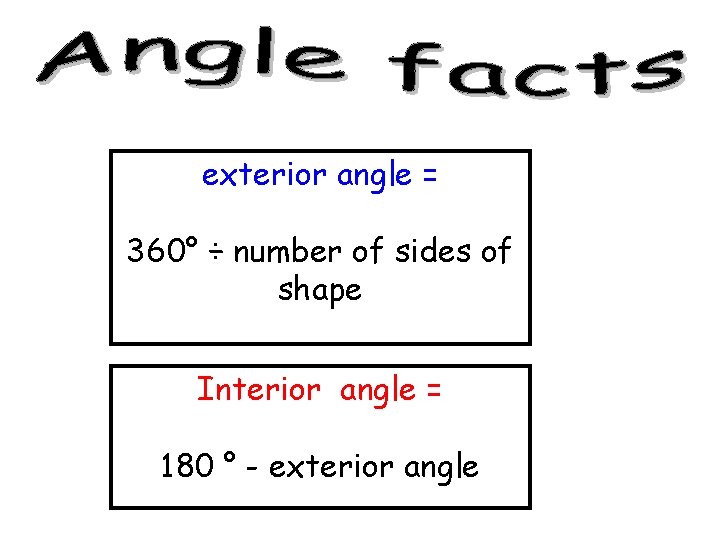
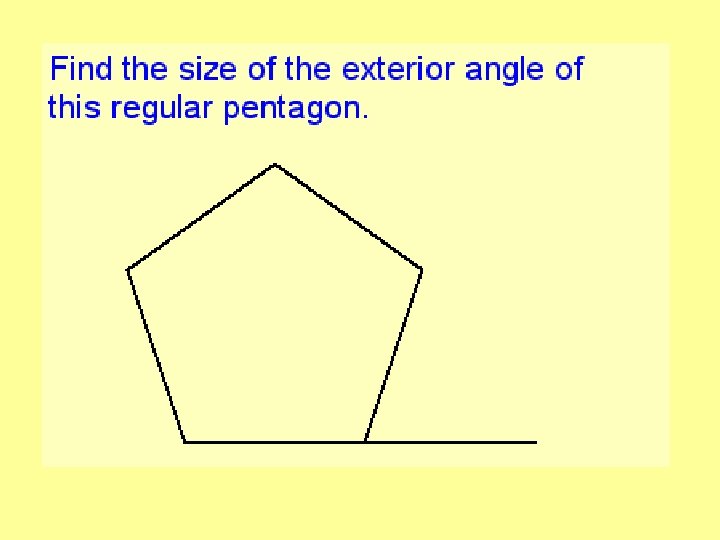
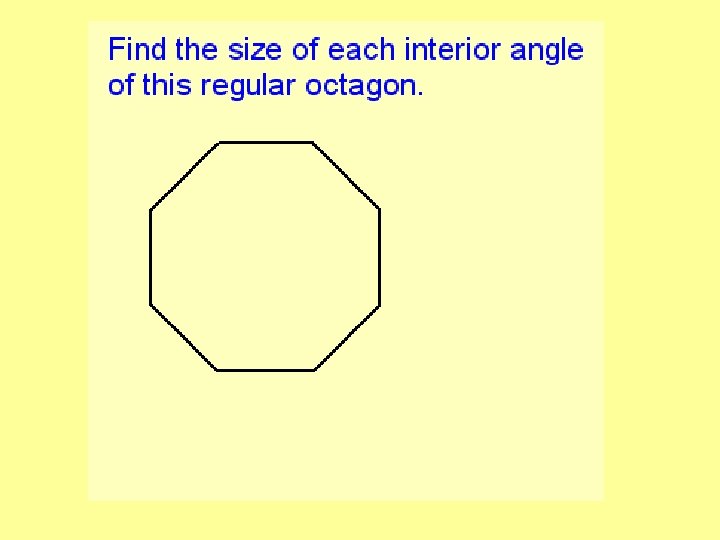
exterior angle = 360° ÷ number of sides of shape Interior angle = 180 ° - exterior angle
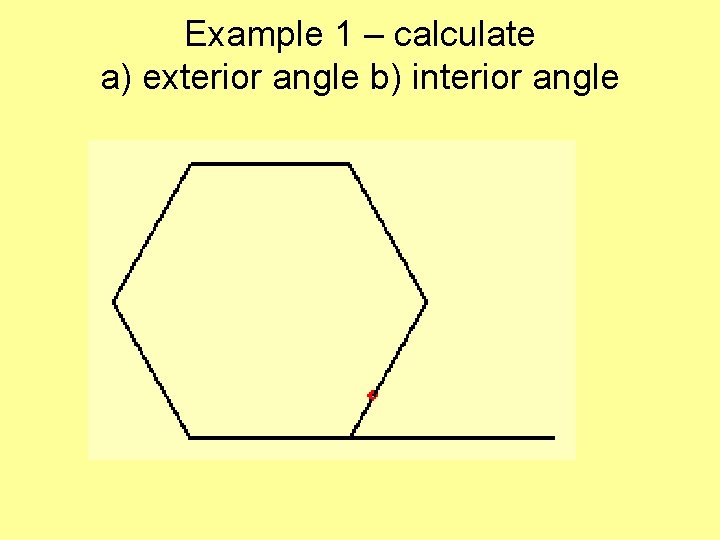
Example 1 – calculate a) exterior angle b) interior angle
- Slides: 62