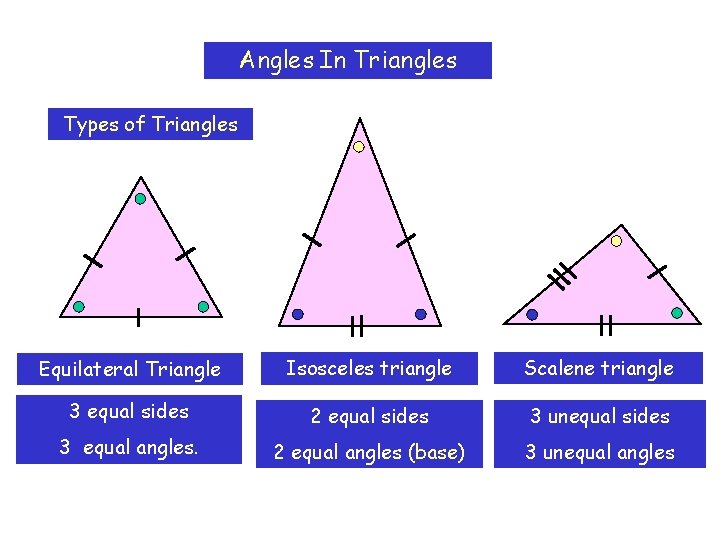
Angles In Triangles Types of Triangles Equilateral Triangle

  • Slides: 16
Download presentation
Angles In Triangles Types of Triangles Equilateral Triangle Isosceles triangle Scalene triangle 3 equal

Angles In Triangles Types of Triangles Equilateral Triangle Isosceles triangle Scalene triangle 3 equal sides 2 equal sides 3 unequal sides 3 equal angles. 2 equal angles (base) 3 unequal angles

Any triangle containing a 90 o angle is a right-angled triangle An isosceles or

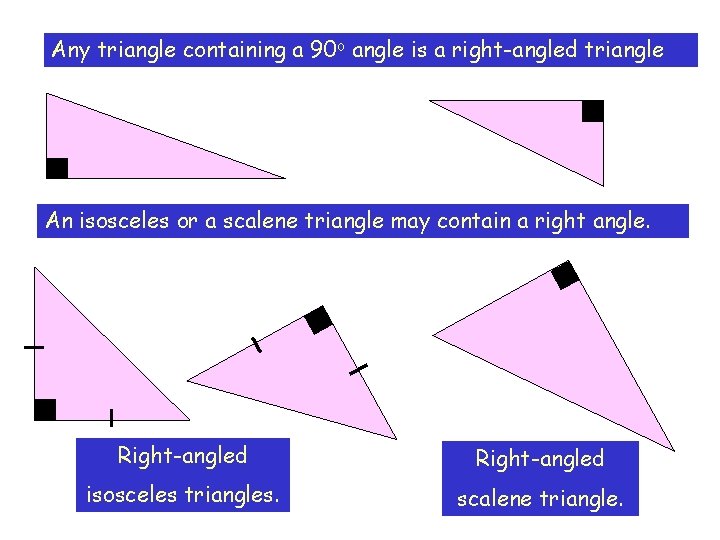
Any triangle containing a 90 o angle is a right-angled triangle An isosceles or a scalene triangle may contain a right angle. Right-angled isosceles triangles. scalene triangle.

To determine the angle sum of any Triangle Take 3 indentical copies of this

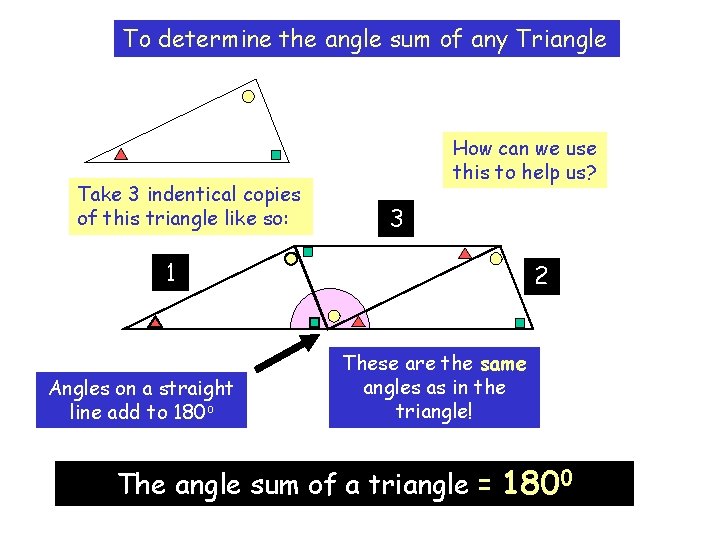
To determine the angle sum of any Triangle Take 3 indentical copies of this triangle like so: How can we use this to help us? 3 1 Angles on a straight line add to 180 o 2 These are the same angles as in the triangle! The angle sum of a triangle = 1800

Calculating unknown Angles Example 1 Calculate angle a. 65 o a Angle a =

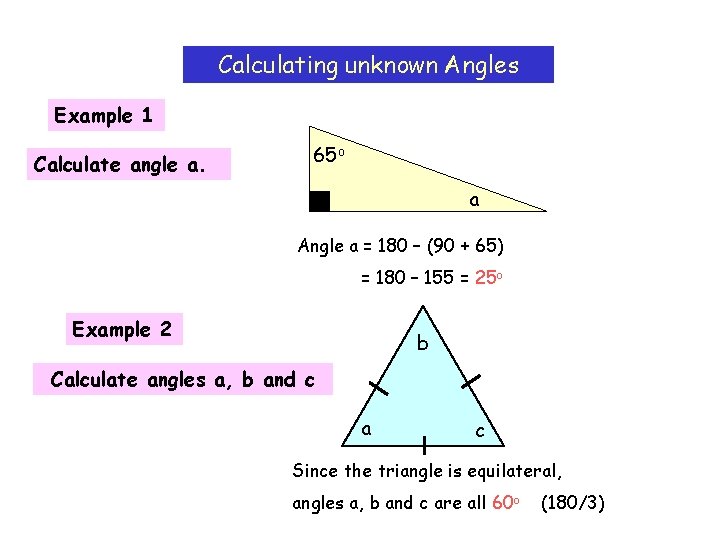
Calculating unknown Angles Example 1 Calculate angle a. 65 o a Angle a = 180 – (90 + 65) = 180 – 155 = 25 o Example 2 b Calculate angles a, b and c a c Since the triangle is equilateral, angles a, b and c are all 60 o (180/3)

Calculating unknown Angles Example 3 b Angle a = 65 o (base angles of

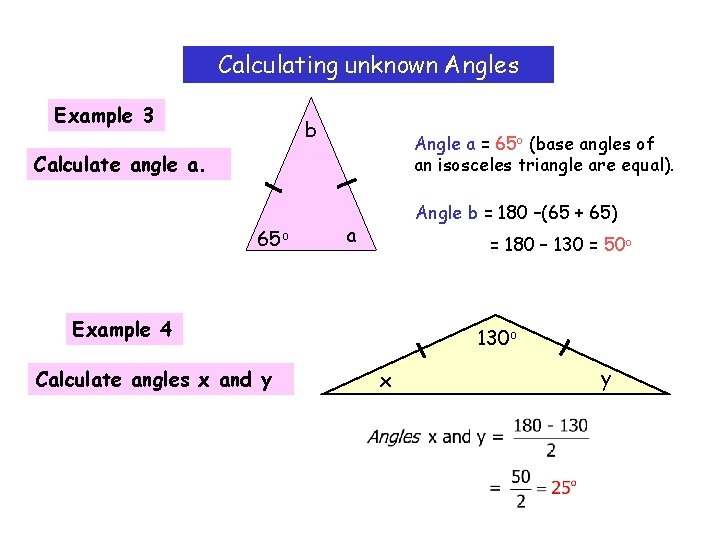
Calculating unknown Angles Example 3 b Angle a = 65 o (base angles of an isosceles triangle are equal). Calculate angle a. 65 o Angle b = 180 –(65 + 65) a = 180 – 130 = 50 o Example 4 Calculate angles x and y 130 o x y

Calculating unknown Angles Example 5 Calculate angles a and b. a b Example 6

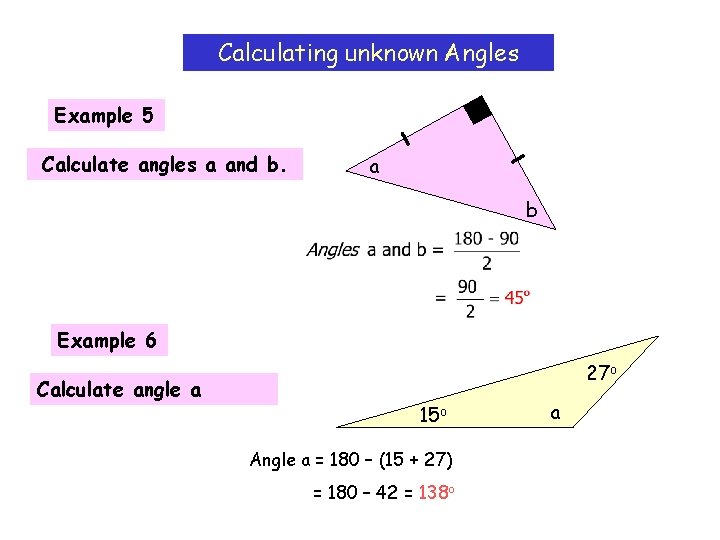
Calculating unknown Angles Example 5 Calculate angles a and b. a b Example 6 Calculate angle a 27 o 15 o Angle a = 180 – (15 + 27) = 180 – 42 = 138 o a

Vertical Angles at a Point Oblique line b = 115 o Horizontal 90 90

Vertical Angles at a Point Oblique line b = 115 o Horizontal 90 90 b a a +–b 115 = 180 Angles a = 180 = 65 o o

Vertical Horizontal Angles at a Point 90 90 360 o 2 1 360 o

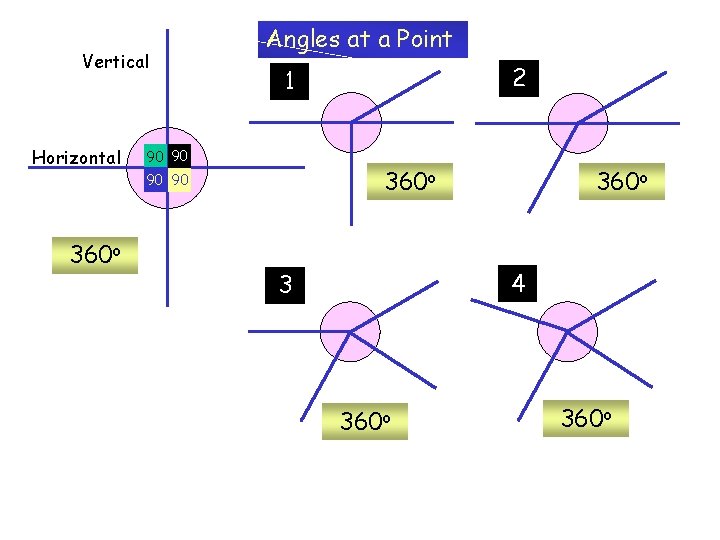
Vertical Horizontal Angles at a Point 90 90 360 o 2 1 360 o 4 3 360 o

Angles at a Point d c b a Angles at a point add to

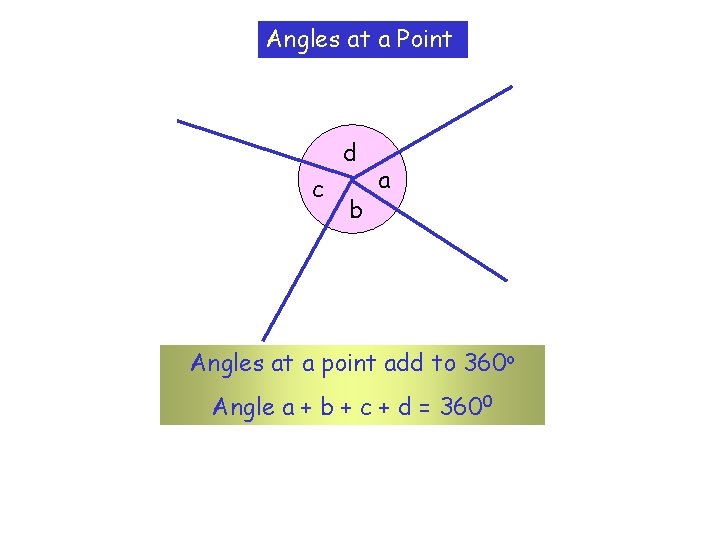
Angles at a Point d c b a Angles at a point add to 360 o Angle a + b + c + d = 3600

Angles at a Point 90 90 Example 1: Find angle a. a 360 o

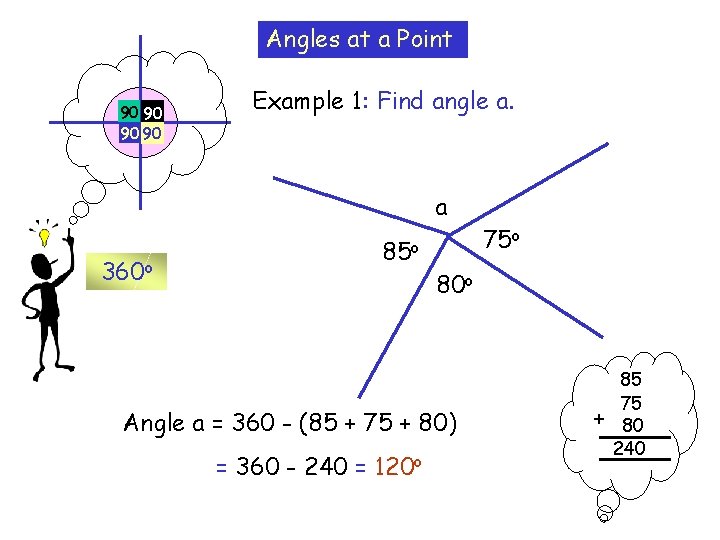
Angles at a Point 90 90 Example 1: Find angle a. a 360 o 85 o 80 o Angle a = 360 - (85 + 75 + 80) = 360 - 240 = 120 o 75 o + 85 75 80 240

Angles at a Point 90 90 Example 2: Find angle x. 105 o x

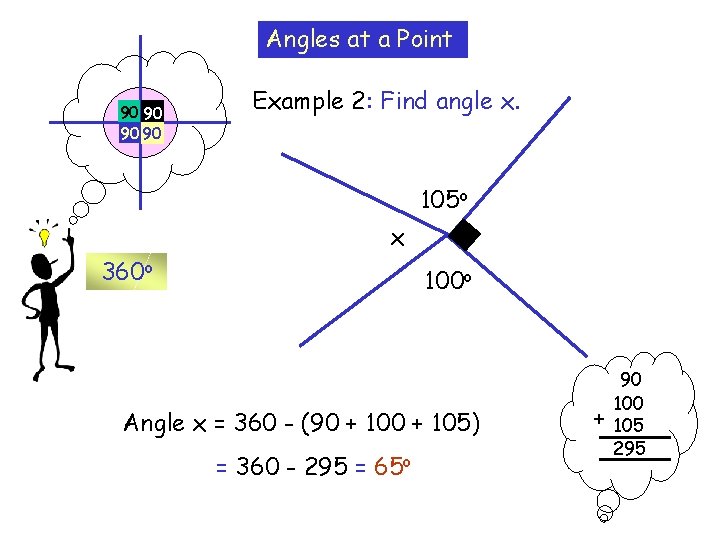
Angles at a Point 90 90 Example 2: Find angle x. 105 o x 360 o 100 o Angle x = 360 - (90 + 105) = 360 - 295 = 65 o + 90 105 295

1 90 o 360 o 2 4 270 o 180 o 3 360 o

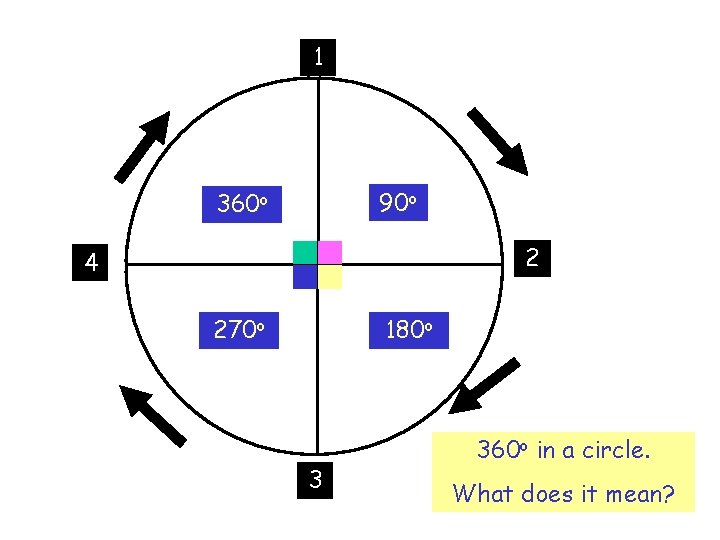
1 90 o 360 o 2 4 270 o 180 o 3 360 o in a circle. What does it mean?

When a vertical line and a horizontal line meet the angle between them is

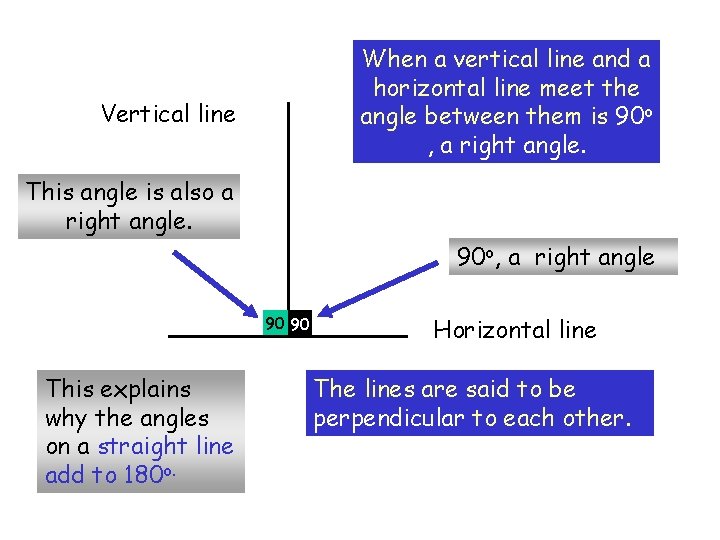
When a vertical line and a horizontal line meet the angle between them is 90 o , a right angle. Vertical line This angle is also a right angle. 90 o, a right angle 90 90 This explains why the angles on a straight line add to 180 o. Horizontal line The lines are said to be perpendicular to each other.

Angles on a straight line add to 180 o Oblique line 90 90 180

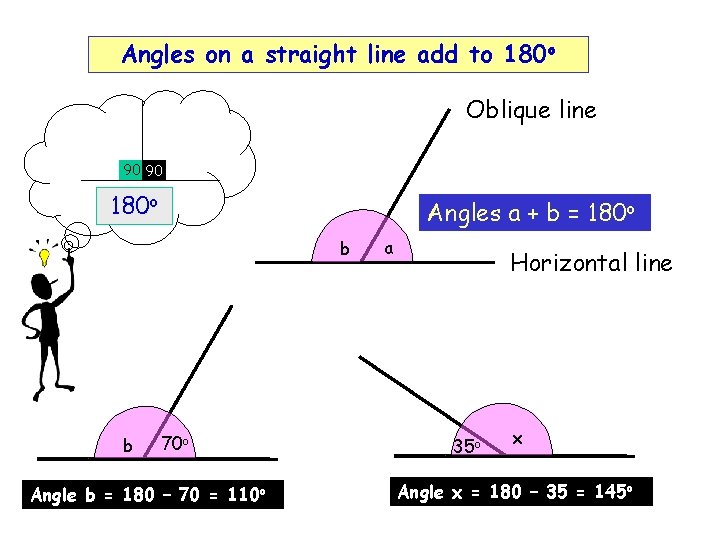
Angles on a straight line add to 180 o Oblique line 90 90 180 o Angles a + b = 180 o b b 70 o Angle b = 180 – 70 = 110 o a Horizontal line 35 o x Angle x = 180 – 35 = 145 o

Find the unknown angles 1 2 y 47 o 114 o x Angle x

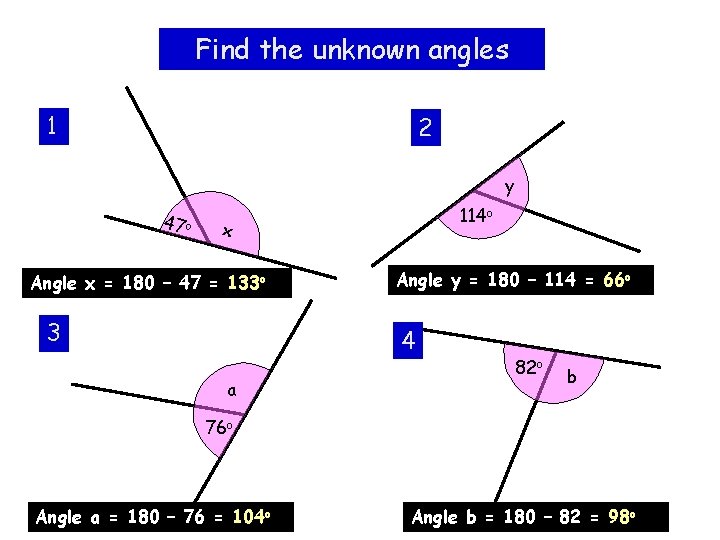
Find the unknown angles 1 2 y 47 o 114 o x Angle x = 180 – 47 = 133 o 3 Angle y = 180 – 114 = 66 o 4 a 82 o b 76 o Angle a = 180 – 76 = 104 o Angle b = 180 – 82 = 98 o