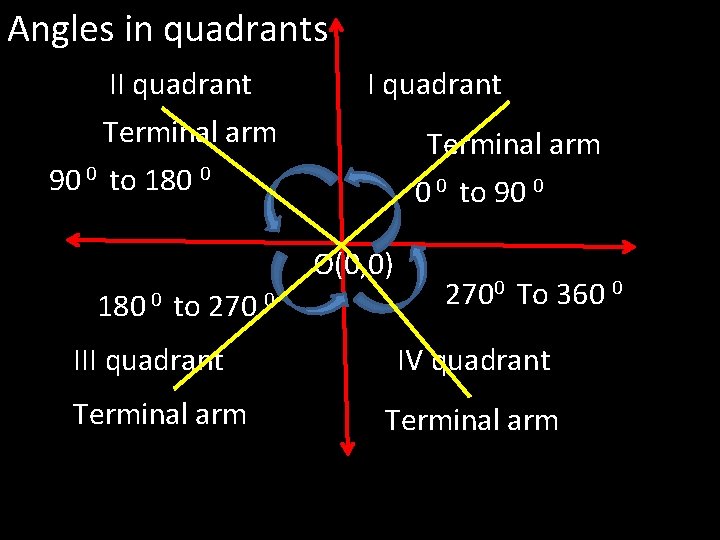
Angles in quadrants II quadrant Terminal arm 90


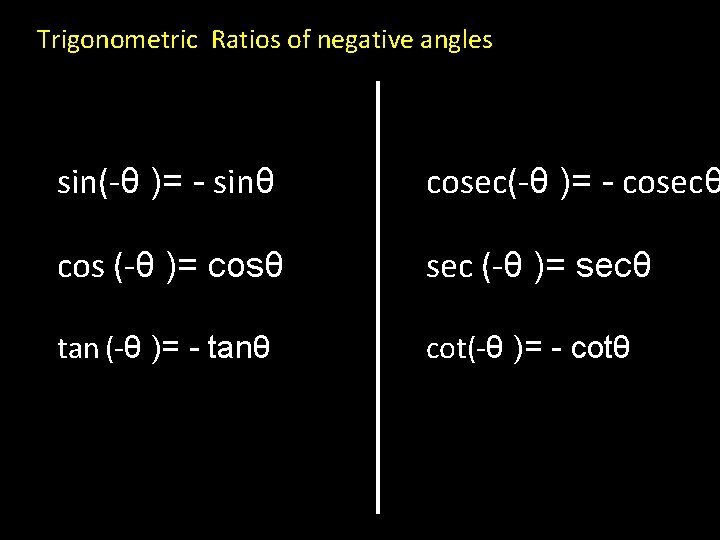
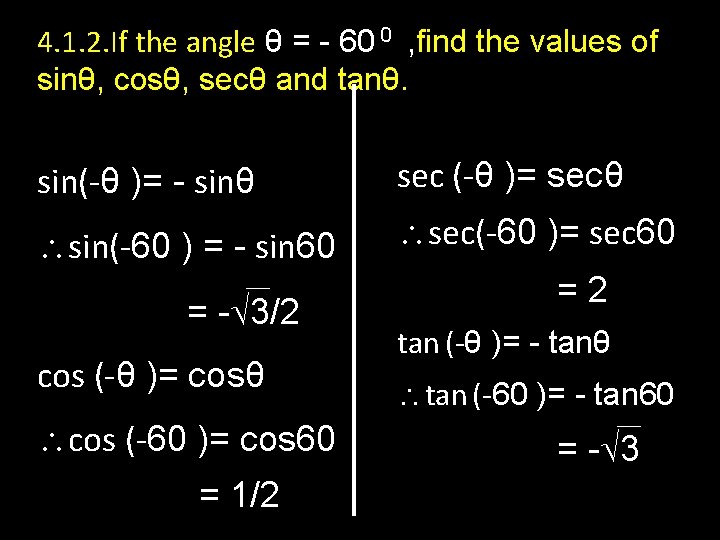

- Slides: 12

Angles in quadrants II quadrant Terminal arm 90 0 to 180 0 Terminal arm 0 0 to 90 0 O(0, 0) 180 0 to 270 III quadrant Terminal arm 0 2700 To 360 0 IV quadrant Terminal arm

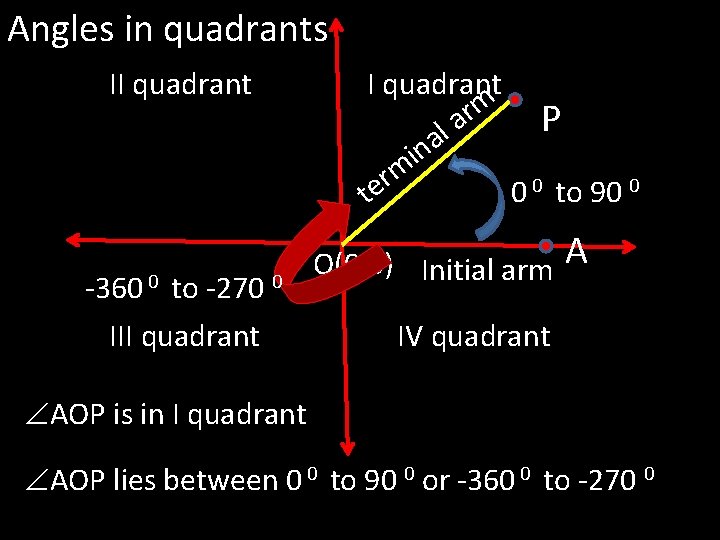
Angles in quadrants II quadrant -360 0 to -270 0 III quadrant m r P a l a n i m r 0 to 90 0 e 0 t O(0, 0) Initial arm A IV quadrant AOP is in I quadrant AOP lies between 0 0 to 90 0 or -360 0 to -270 0

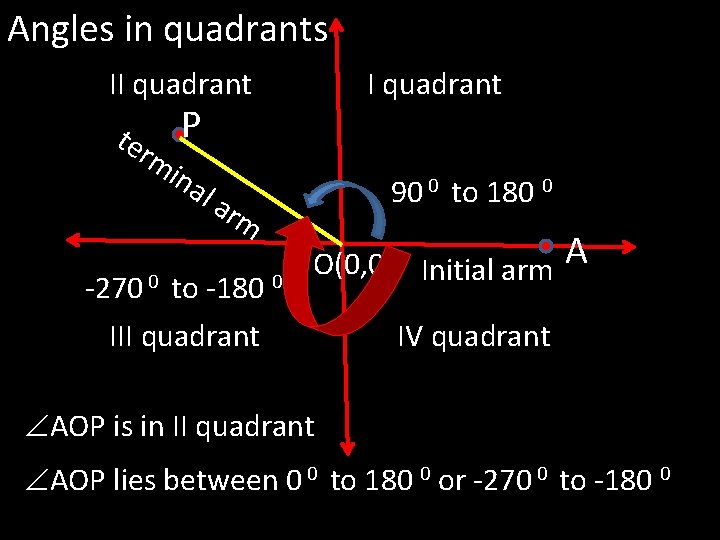
Angles in quadrants II quadrant P ter m ina la 90 0 to 180 0 rm -270 0 to -180 0 III quadrant O(0, 0) Initial arm A IV quadrant AOP is in II quadrant AOP lies between 0 0 to 180 0 or -270 0 to -180 0

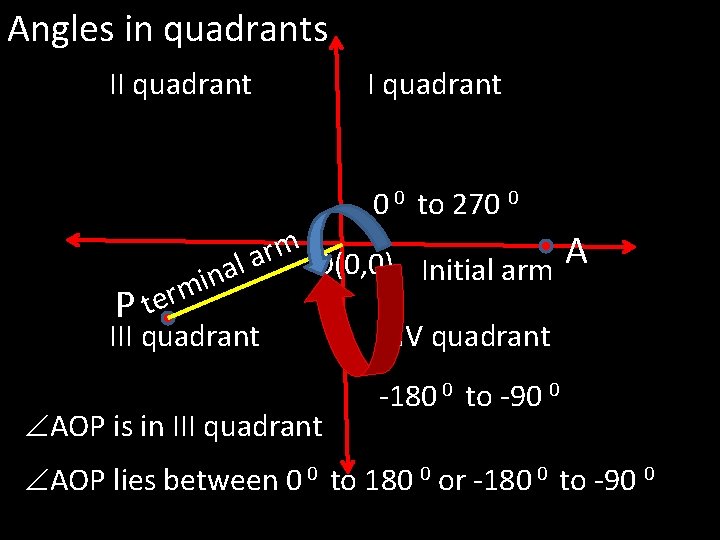
Angles in quadrants II quadrant 0 0 to 270 0 m r a O(0, 0) Initial arm l a n i m r e t P III quadrant AOP is in III quadrant A IV quadrant -180 0 to -90 0 AOP lies between 0 0 to 180 0 or -180 0 to -90 0

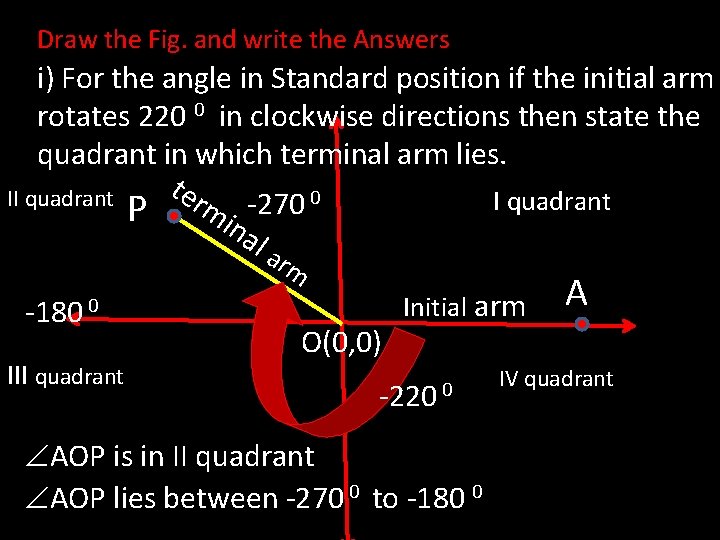
Draw the Fig. and write the Answers i) For the angle in Standard position if the initial arm rotates 220 0 in clockwise directions then state the quadrant in which terminal arm lies. ter 0 II quadrant -270 m P ina la rm -180 0 III quadrant O(0, 0) Initial arm -220 0 AOP is in II quadrant AOP lies between -270 0 to -180 0 A IV quadrant

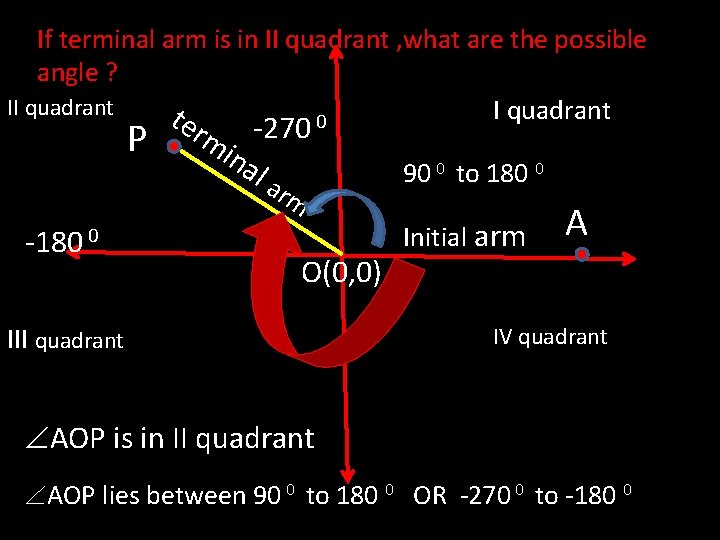
If terminal arm is in II quadrant , what are the possible angle ? II quadrant te 0 P -270 ina la rm rm -180 0 O(0, 0) III quadrant 90 0 to 180 0 Initial arm A IV quadrant AOP is in II quadrant AOP lies between 90 0 to 180 0 OR -270 0 to -180 0

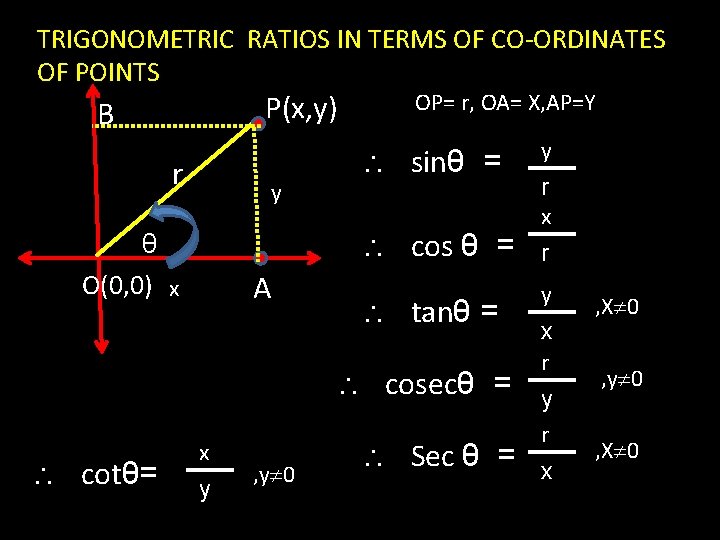
TRIGONOMETRIC RATIOS IN TERMS OF CO-ORDINATES OF POINTS P(x, y) B r y θ O(0, 0) x A OP= r, OA= X, AP=Y sinθ = y cos θ = r tanθ = cosecθ = cotθ= x y , y 0 Sec θ = r x y x r y r x , X 0 , y 0 , X 0

Sings of Trigonometric ratios in different quadtants I quadrant II quadrant (- , + ) (+ , +) Sine positive All are positive O(0, 0) III quadrant IV quadrant (- , - ) (+ , - ) tangent positive cosine positive

4. 2. 1 Find the trigonometric ratios in standard position whoes terminal arm passes through the points X=4, y=3 r = x 2+ y 2 r = 4 2+ 3 2 r = 16 + 9 r = 25 (i) ( 4, 3) (ii) ( 5 , - 12 ) y sinθ = cos θ = tanθ = cosecθ = r = 5 cotθ= x y =3/4 Sec θ = r x r y r x =3/5 =4/5 =3/4 =5/3
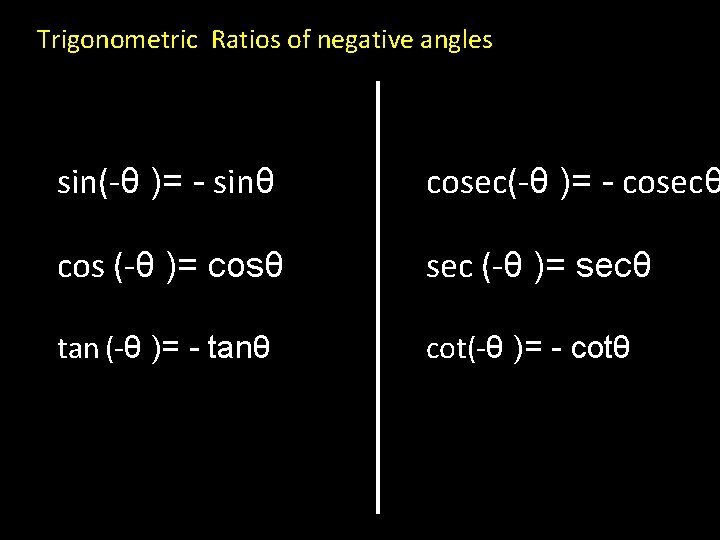
Trigonometric Ratios of negative angles sin(-θ )= - sinθ cosec(-θ )= - cosecθ cos (-θ )= cosθ sec (-θ )= secθ tan (-θ )= - tanθ cot(-θ )= - cotθ
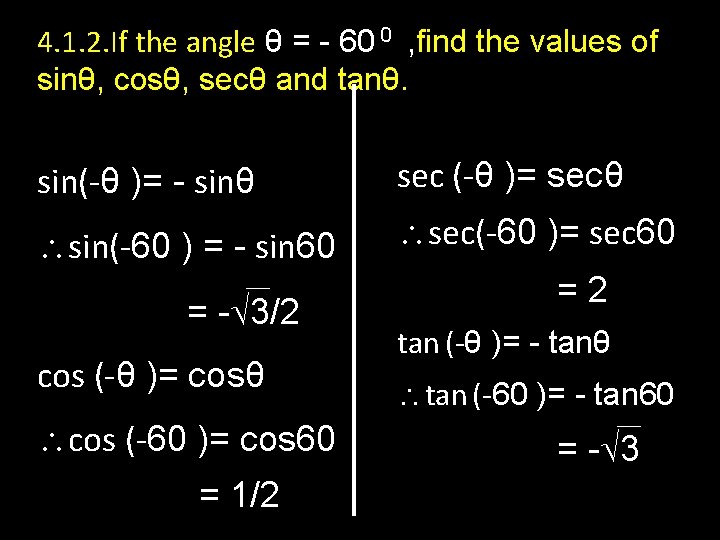
4. 1. 2. If the angle θ = - 60 0 , find the values of sinθ, cosθ, secθ and tanθ. sin(-θ )= - sinθ sec (-θ )= secθ sin(-60 ) = - sin 60 sec(-60 )= sec 60 = - 3/2 cos (-θ )= cosθ cos (-60 )= cos 60 = 1/2 =2 tan (-θ )= - tanθ tan (-60 )= - tan 60 = - 3

4. 2. 3 Find whether the angle lies if the terminal arm passes In Which quadrant pt. (-8, 1) lies? through the following points i)(5, -7) ii)(-8, 1) iii)(-3, -3) iv)(0, 2) In Which quadrant (-8 , 1 ) II quadrant pt. (5, -7) lies? (0 , 2 ) O(0, 0) (-3 , -3 ) IV quadrant (5 , -7 )