Angles In Depth Resources problems and approaches Teaching

Angles In Depth Resources, problems and approaches

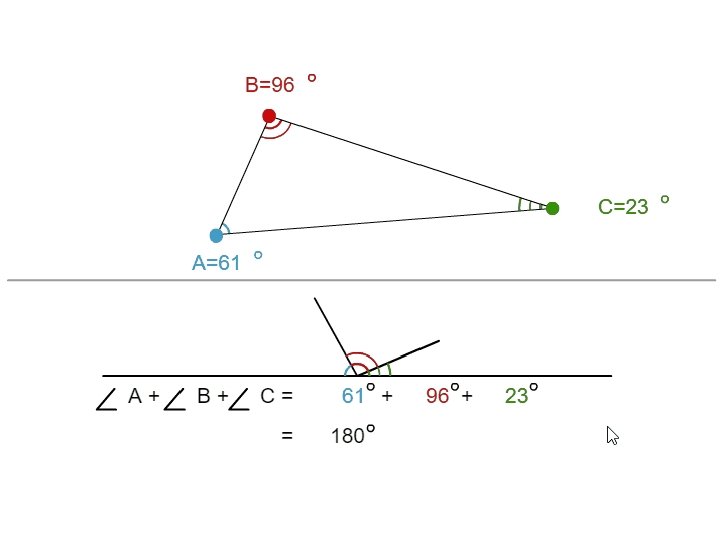
Teaching Year 7 angles for the first time? What to think about. . . • • • Topic progression Primary curriculum Assessment Misconceptions Resources Stretch and challenge

What do they do in primary school? Year 2 Rotation in terms of right angles for quarter, half and three-quarter turns Year 3 Angles as a description of turn. Use accurate language (acute and obtuse). Year 4 Order angles by size. Classify shapes (including types of triangle and types of quadrilateral).

Year 5 Draw, measure, estimate and compare angles in degrees. Identify right angles, angles at a point and angles on a straight line. Year 6 Find missing angles in triangles and quadrilaterals (eg parallelograms). Find missing angles at a point or on a straight line (including vertically opposite angles). Relationships may be expressed algebraically.

Year 5 – Doodle Maths

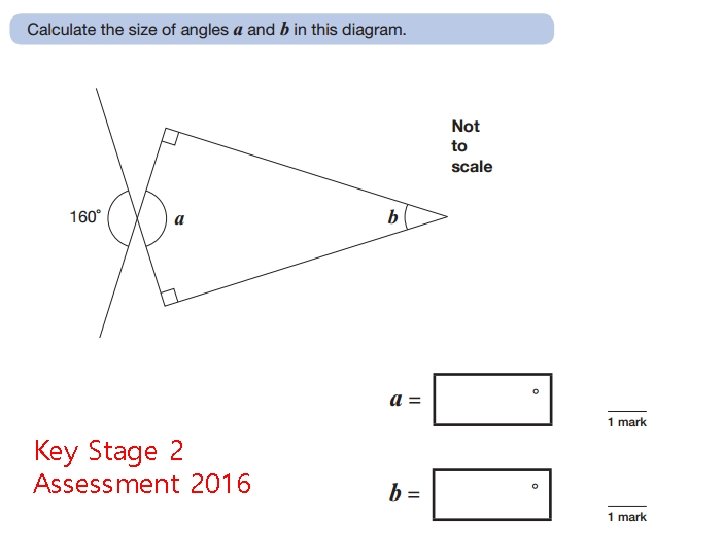
Key Stage 2 Assessment 2016

Key Stage 2 Sample Assessment

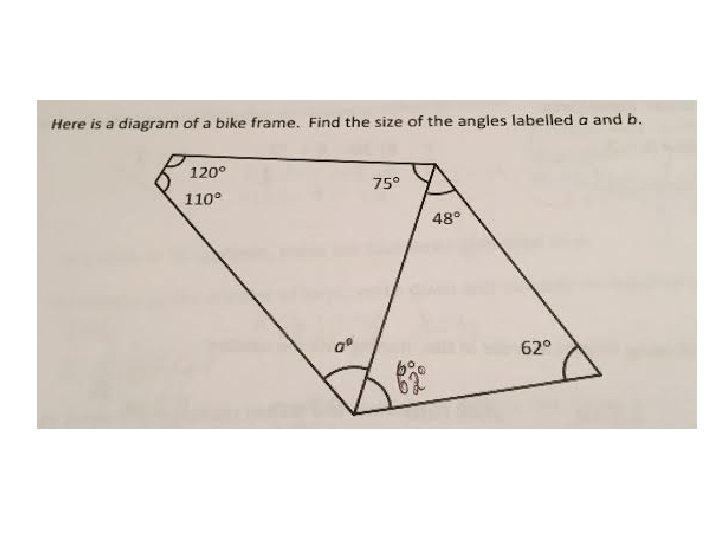
My Year 7 s. . .

Starting over. . . ? Assessment ⇢ Narrative ⇢ Vocabulary and Notation ⇢ Instruction and Practice ⇢ Assessment ⇢ Distributed Practice

Notation, drawing, measuring, estimating Straight lines, around a point, vertically opposite Angles in triangles and quadrilaterals Quadrilateral properties Angles in parallel lines Angles in polygons and tessellation Bearings Leading to – circle theorems, trigonometry Linked to – similarity, congruence, constructions

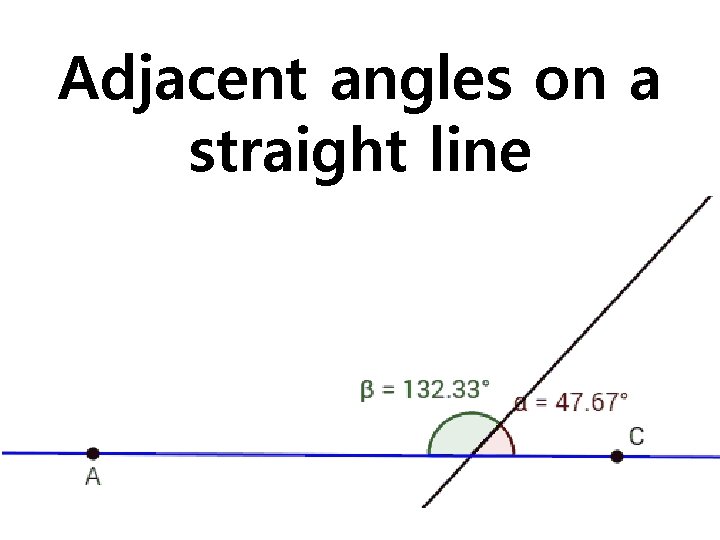
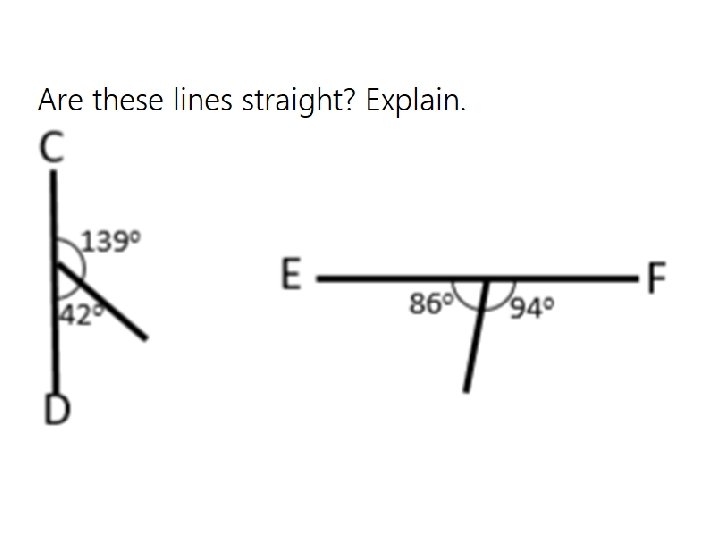
Adjacent angles on a straight line

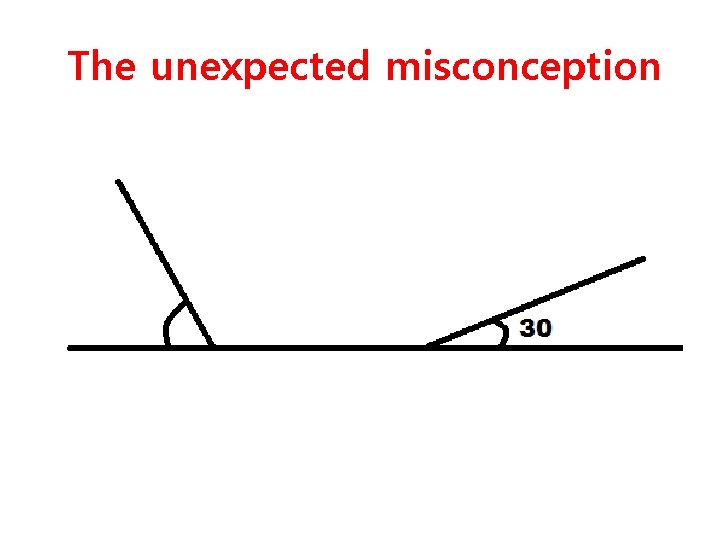
The unexpected misconception

Say “angles that form a straight line” or “adjacent angles on a straight line” or “angles at a point on one side of a straight line” but avoid the ambiguous “angles on a straight line”

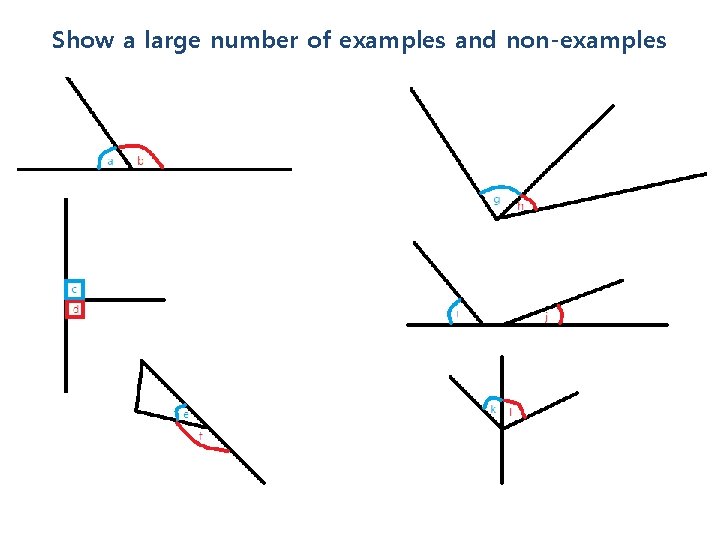
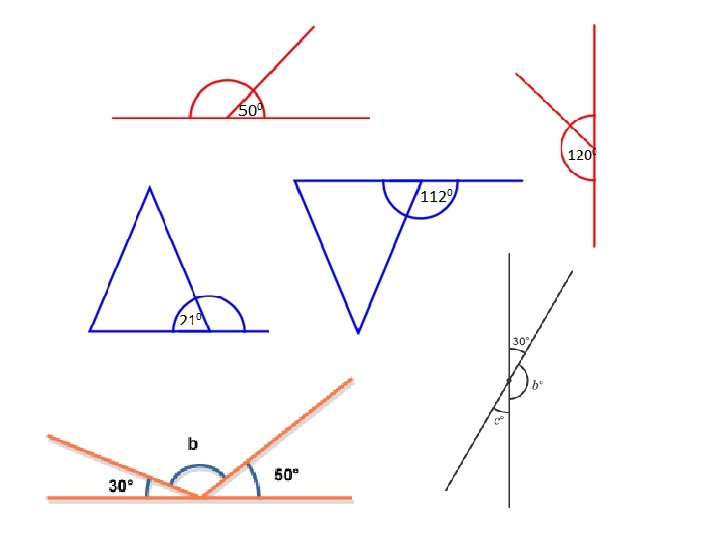
Show a large number of examples and non-examples

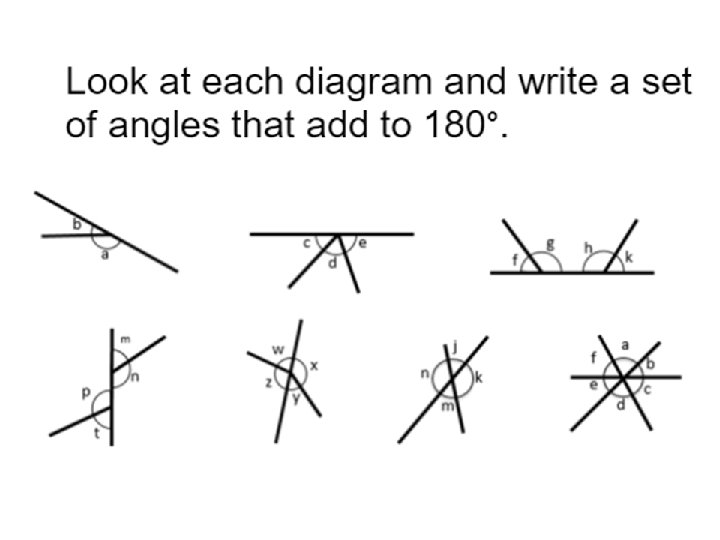
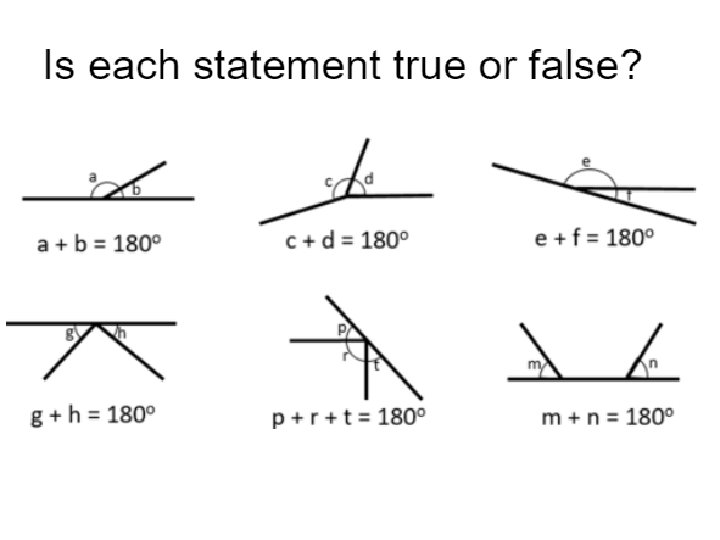
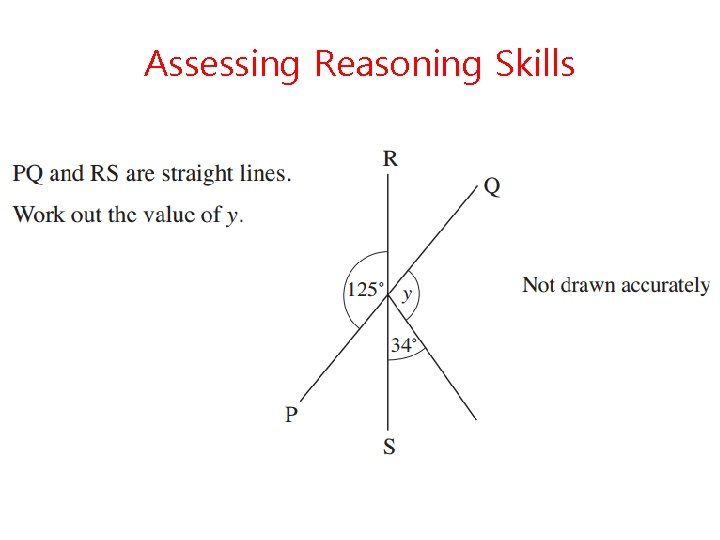
Assessing Reasoning Skills

Interior Angles in a Triangle

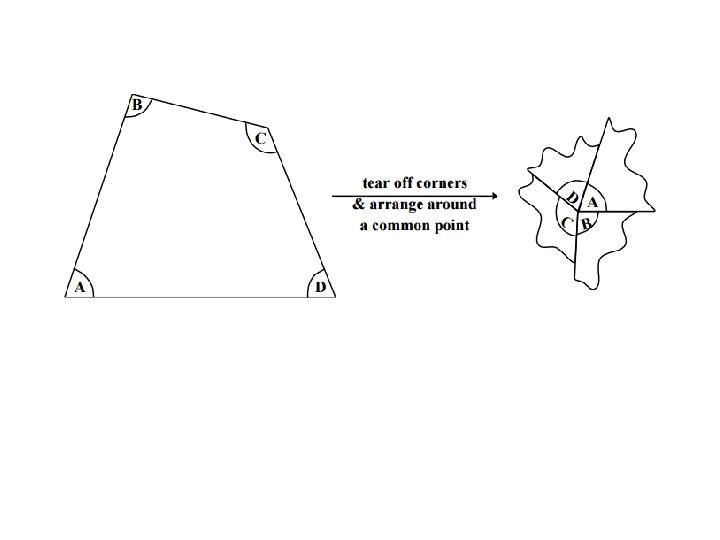
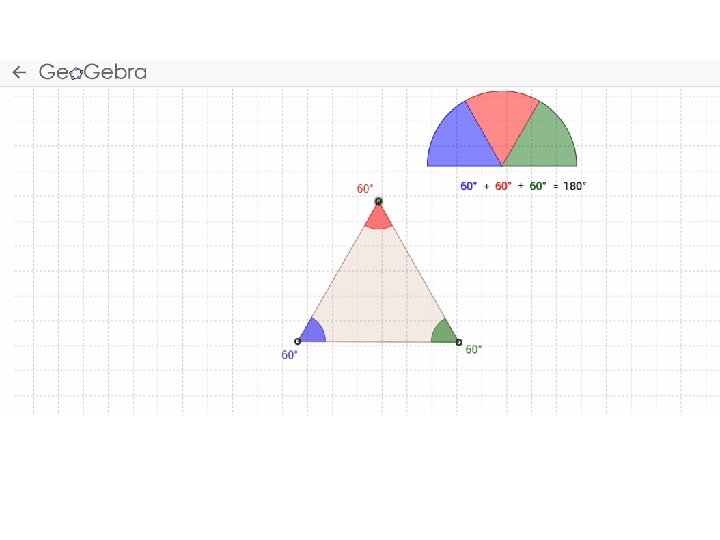
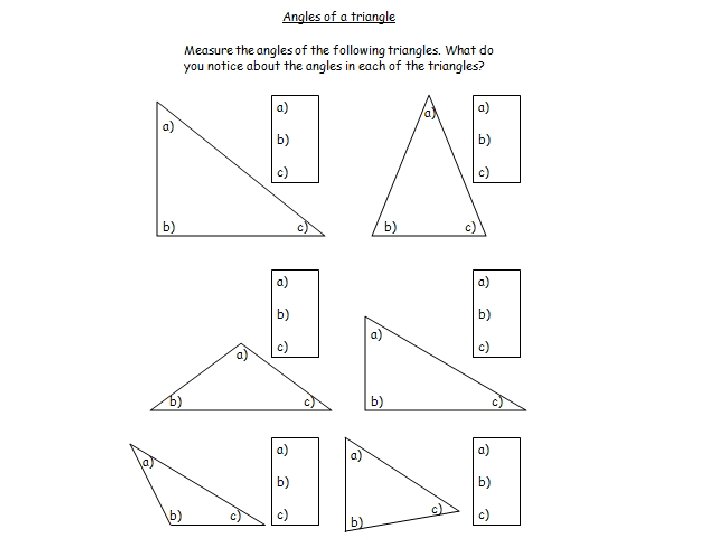
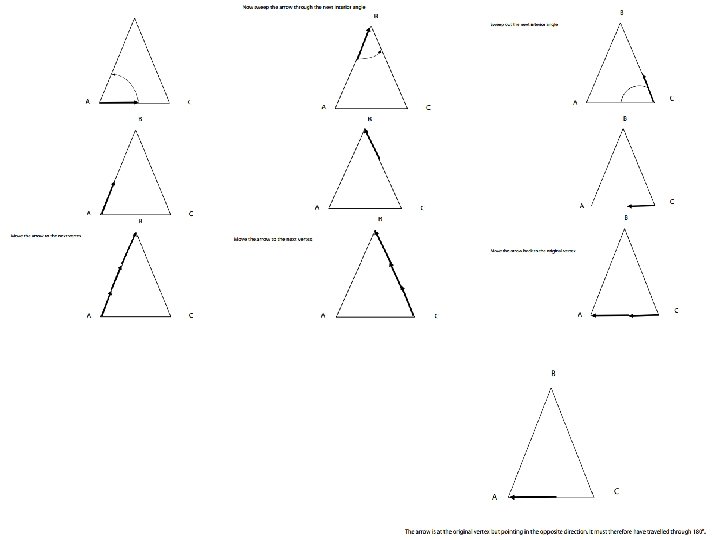
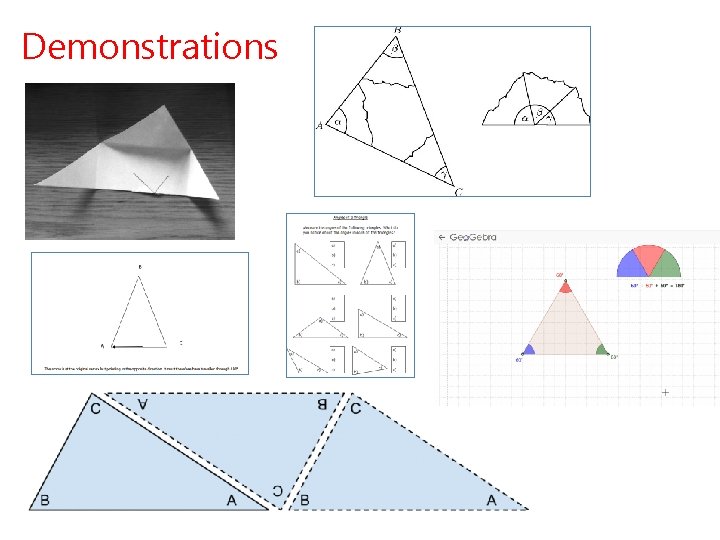
Demonstrations

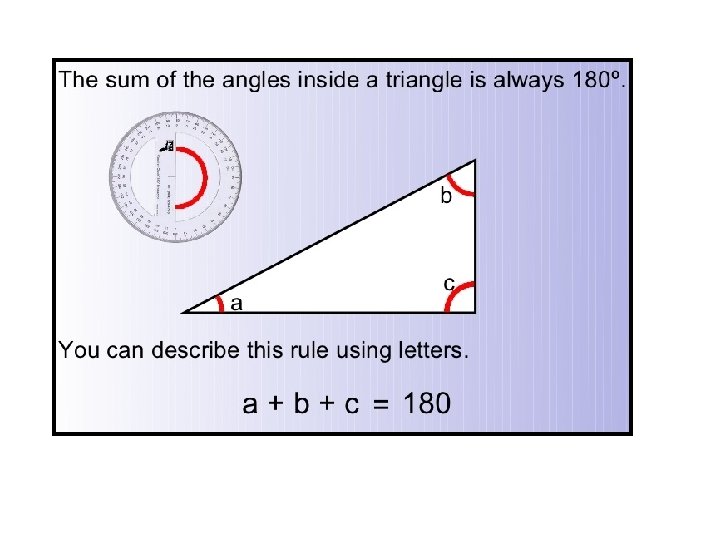
Proof comes later. . .

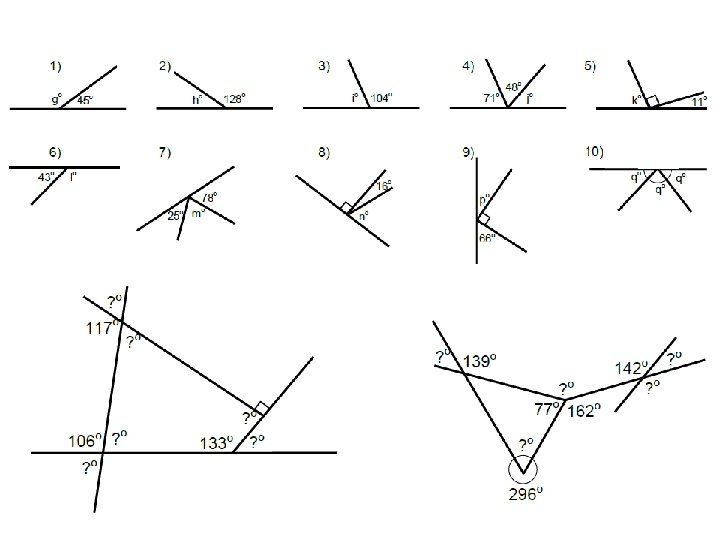
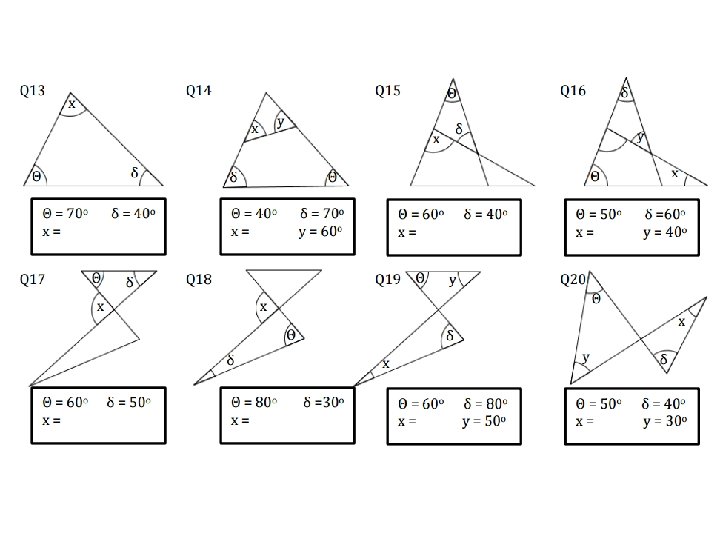
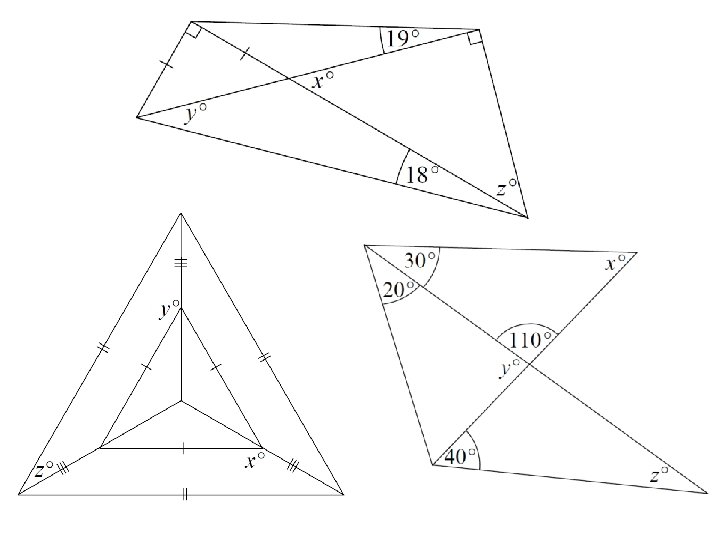
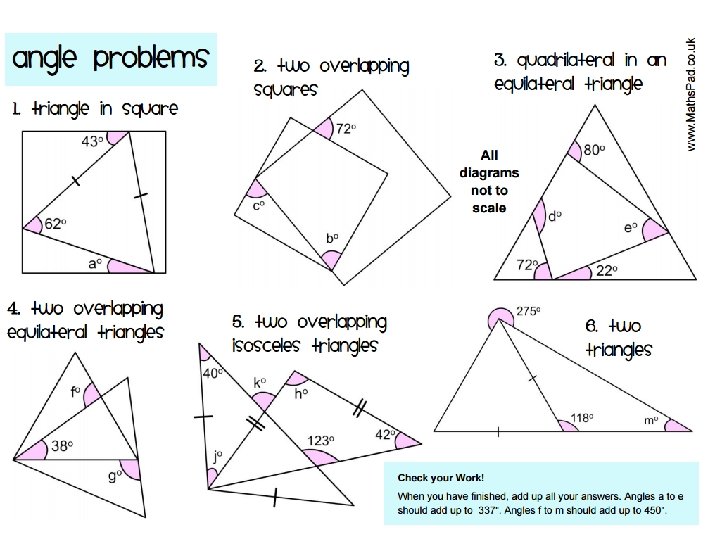
Practice – finding missing angles

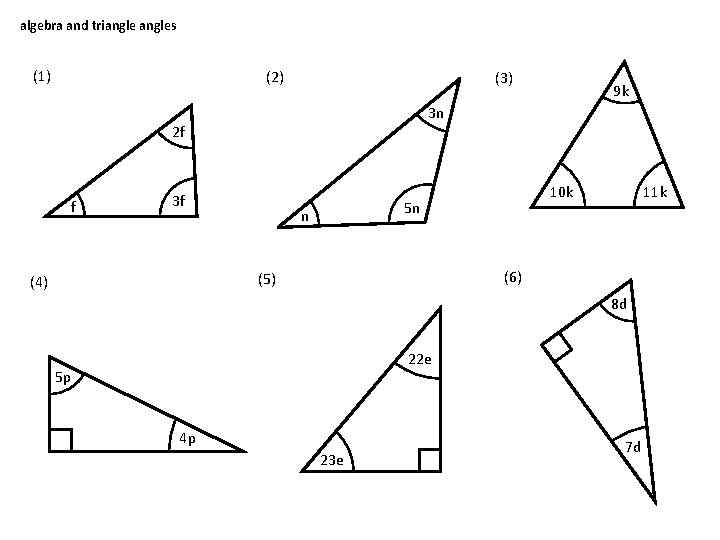
algebra and triangles (1) (2) (3) 3 n 2 f f 3 f 11 k 10 k 5 n n (6) (5) (4) 9 k 8 d 22 e 5 p 4 p 23 e 7 d

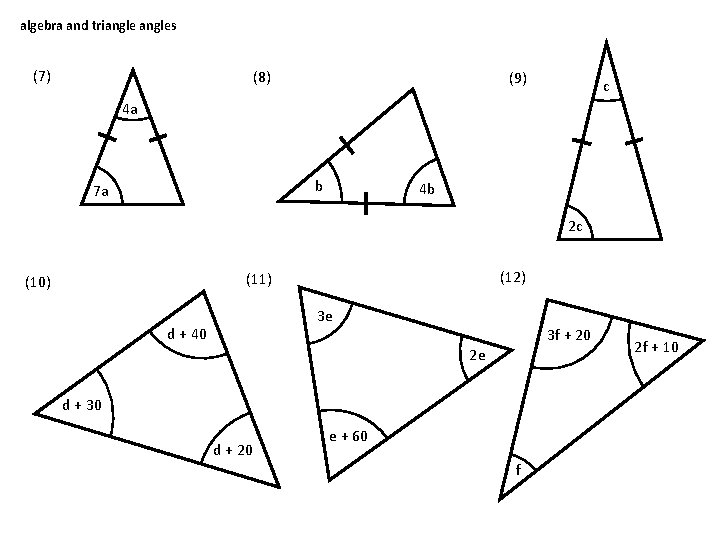
algebra and triangles (7) (8) (9) c 4 a b 7 a 4 b 2 c (12) (11) (10) 3 e d + 40 3 f + 20 2 e d + 30 d + 20 e + 60 f 2 f + 10

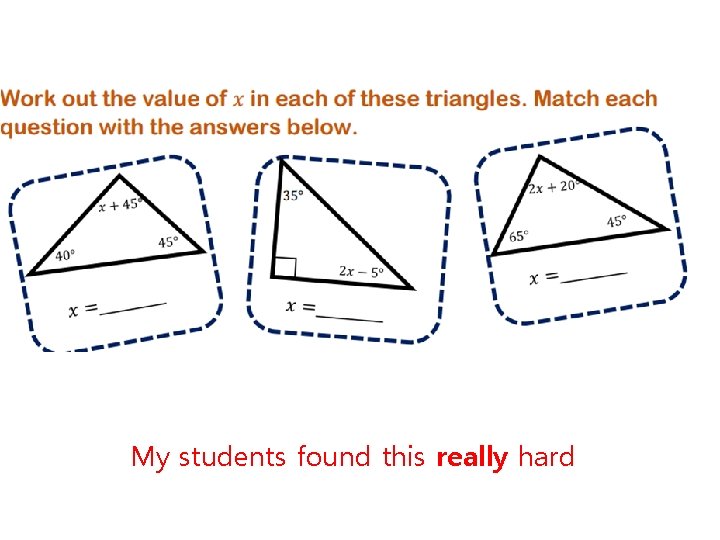
My students found this really hard

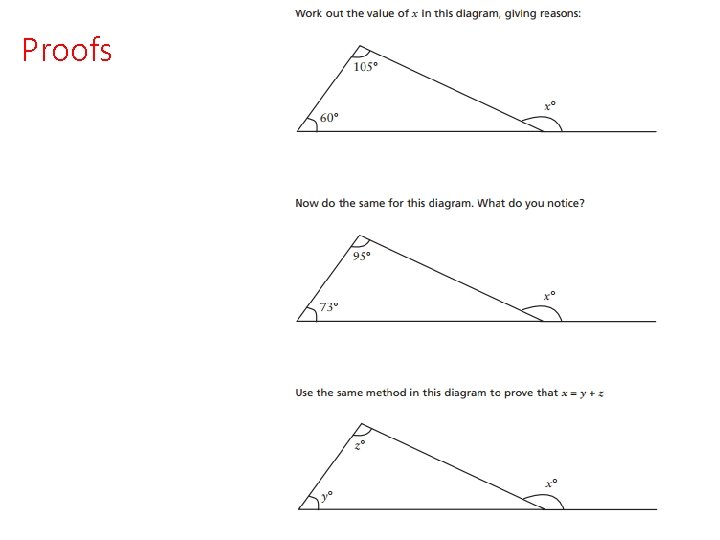
Proofs

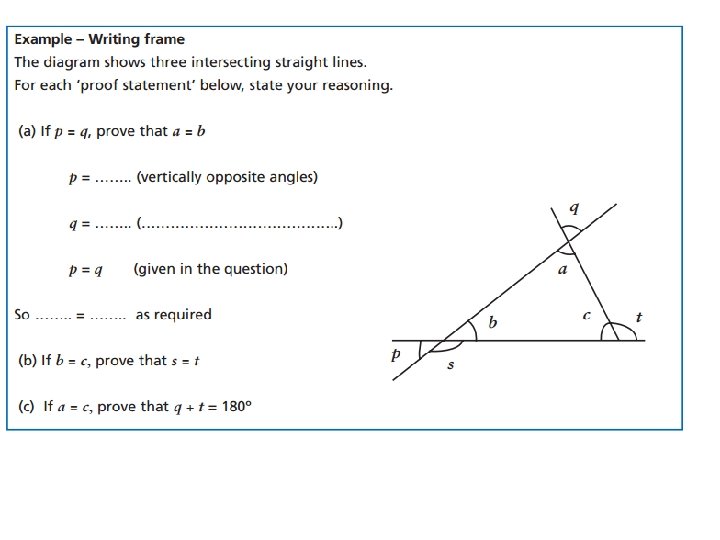
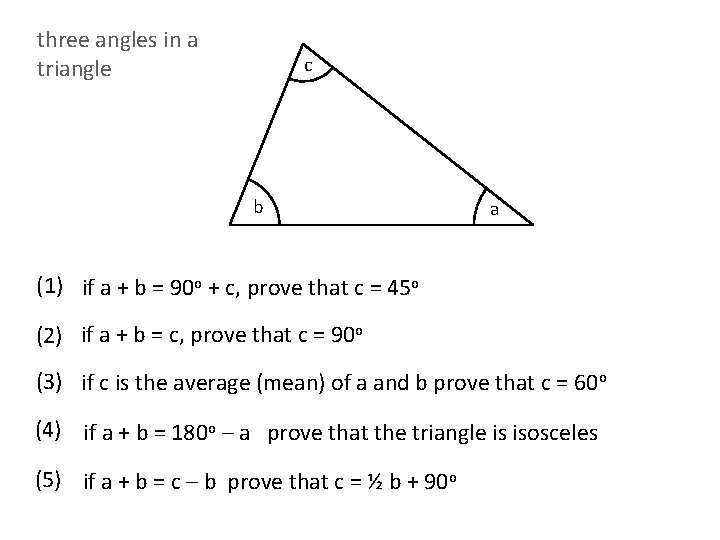
three angles in a triangle c b a (1) if a + b = 90 o + c, prove that c = 45 o (2) if a + b = c, prove that c = 90 o (3) if c is the average (mean) of a and b prove that c = 60 o (4) if a + b = 180 o – a prove that the triangle is isosceles (5) if a + b = c – b prove that c = ½ b + 90 o

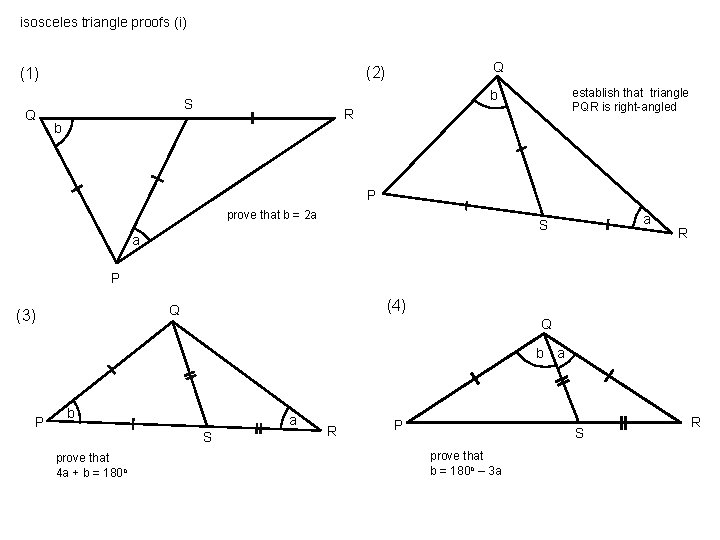
isosceles triangle proofs (i) Q Q (2) (1) establish that triangle PQR is right-angled b S R b P prove that b = 2 a a S a R P (4) Q (3) Q b a P b a S prove that 4 a + b = 180 o R P S prove that b = 180 o – 3 a R

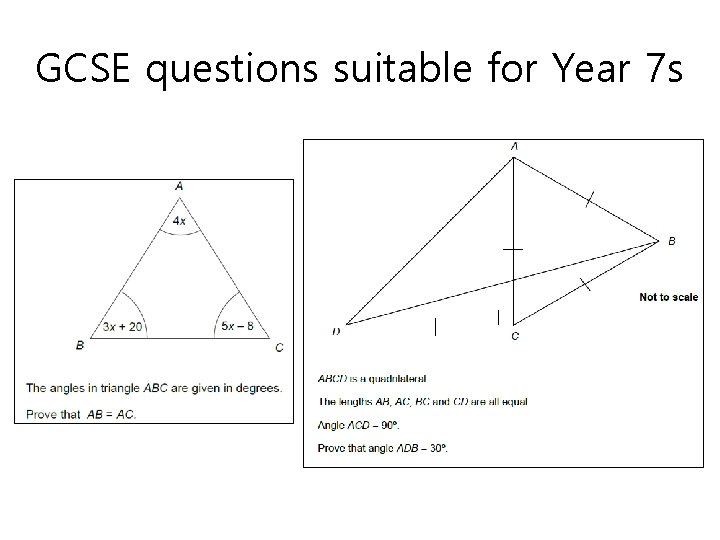
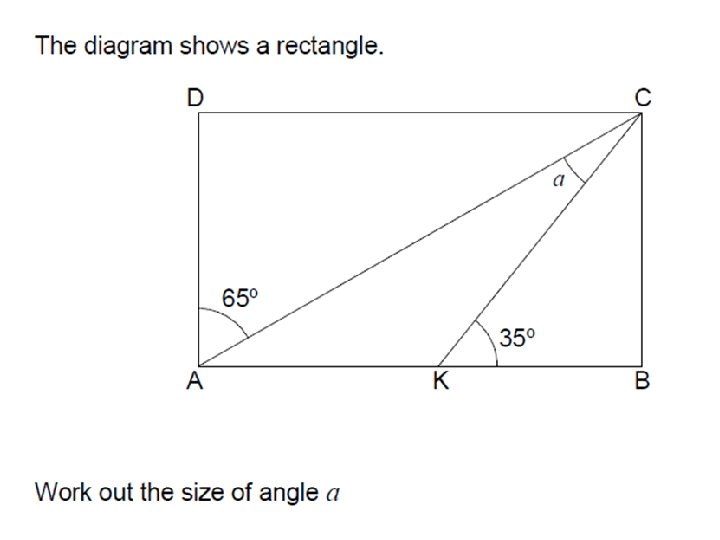
GCSE questions suitable for Year 7 s

Problem Solving

How many lessons can we spend looking at angles in triangles?

Resources. . . ü Maths. Pad ü Don Steward ü Malakiss ü Solve My Maths ü CIMT ü Dr Frost (including proofs) ü Corbett Maths ü White Rose Maths Hub ü Resourceaholic. com