ANGLES AND THE UNIT CIRCLE CREATING THE UNIT

THE UNIT CIRCLE DEFINITION: A CIRCLE CENTERED AT THE ORIGIN WITH A RADIUS OF

THE UNIT CIRCLE The Unit Circle - Radius is always one unit - Center

WHAT ARE THE ANGLE MEASUREMENTS OF EACH OF THE FOUR ANGLES 90° 0° 180°

THE UNIT CIRCLE LET’S LOOK AT AN EXAMPLE THE X-COORDINATE OF THIS HAS A

THE UNIT CIRCLE Create a right triangle, using 1 45 -1 1 the following

45° REFERENCE ANGLES - COORDINATES REMEMBER THAT THE UNIT CIRCLE IS OVERLAYED ON A

THE UNIT CIRCLE 1 30 -1 1 Create a right triangle, using the following

60° REFERENCE ANGLES - COORDINATES USE THE SIDE LENGTHS WE LABELED ON THE QI

30° REFERENCE ANGLES WE KNOW THAT THE QUADRANT ONE ANGLE FORMED BY THE TRIANGLE

30° REFERENCE ANGLES - COORDINATES USE THE SIDE LENGTHS WE LABELED ON THE QI

Slides: 13

Download presentation

ANGLES AND THE UNIT CIRCLE CREATING THE UNIT CIRCLE

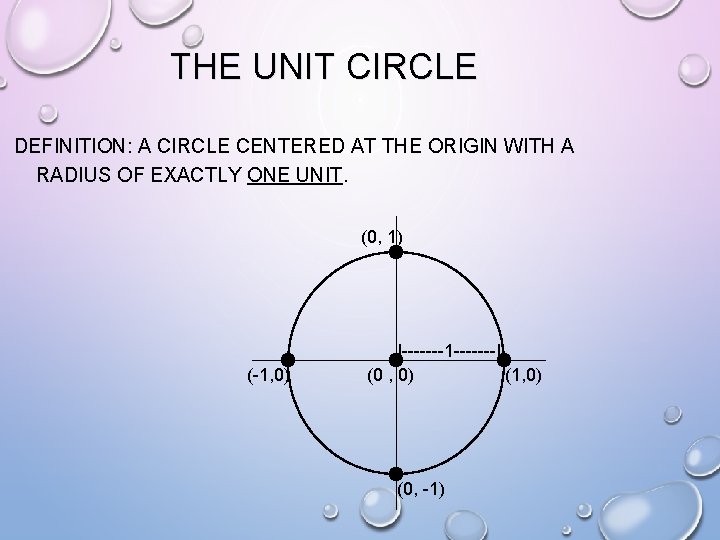
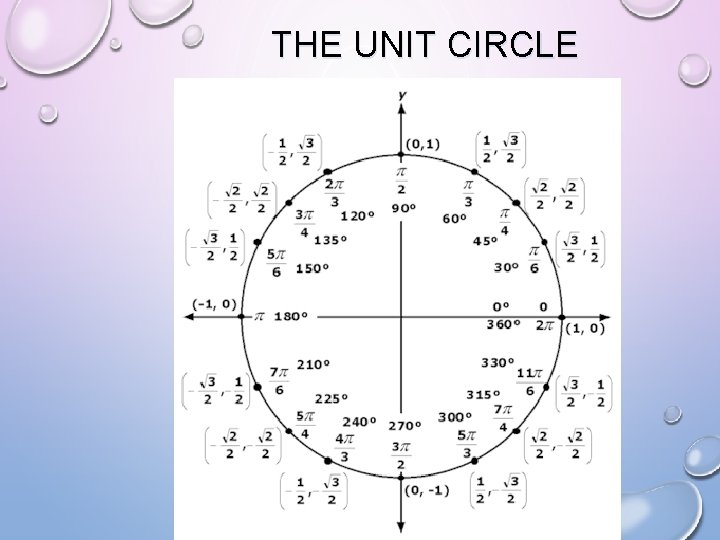
THE UNIT CIRCLE DEFINITION: A CIRCLE CENTERED AT THE ORIGIN WITH A RADIUS OF EXACTLY ONE UNIT. (0, 1) (-1, 0) |-------1 -------| (0 , 0) (1, 0) (0, -1)

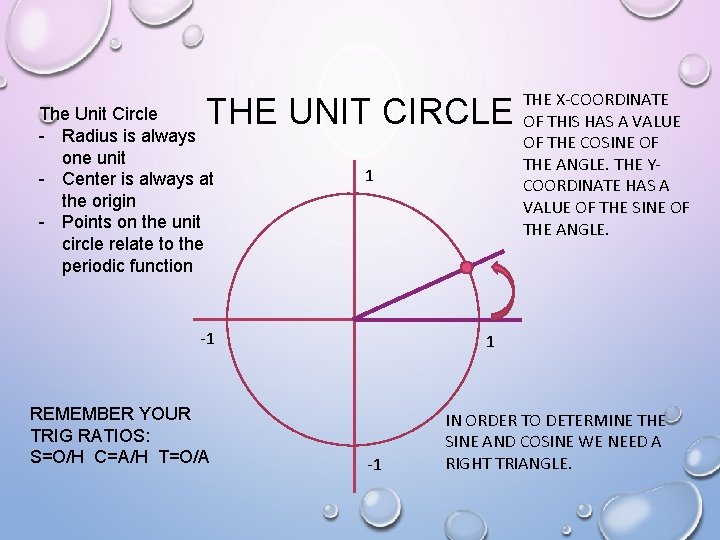
THE UNIT CIRCLE The Unit Circle - Radius is always one unit - Center is always at the origin - Points on the unit circle relate to the periodic function 1 -1 REMEMBER YOUR TRIG RATIOS: S=O/H C=A/H T=O/A THE X-COORDINATE OF THIS HAS A VALUE OF THE COSINE OF THE ANGLE. THE YCOORDINATE HAS A VALUE OF THE SINE OF THE ANGLE. 1 -1 IN ORDER TO DETERMINE THE SINE AND COSINE WE NEED A RIGHT TRIANGLE.

WHAT ARE THE ANGLE MEASUREMENTS OF EACH OF THE FOUR ANGLES 90° 0° 180° 360° 270°

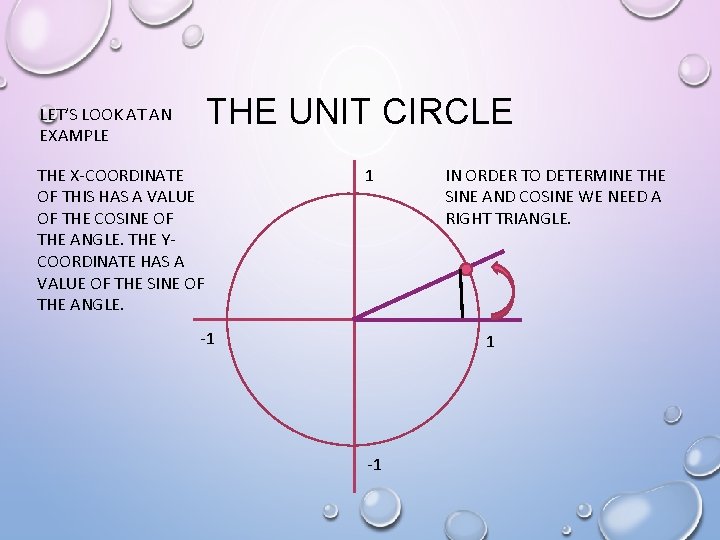
THE UNIT CIRCLE LET’S LOOK AT AN EXAMPLE THE X-COORDINATE OF THIS HAS A VALUE OF THE COSINE OF THE ANGLE. THE YCOORDINATE HAS A VALUE OF THE SINE OF THE ANGLE. 1 -1 IN ORDER TO DETERMINE THE SINE AND COSINE WE NEED A RIGHT TRIANGLE. 1 -1

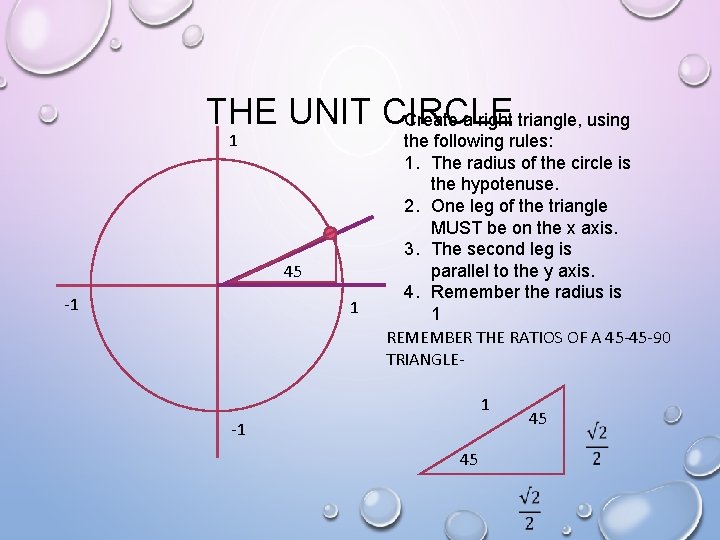
THE UNIT CIRCLE Create a right triangle, using 1 45 -1 1 the following rules: 1. The radius of the circle is the hypotenuse. 2. One leg of the triangle MUST be on the x axis. 3. The second leg is parallel to the y axis. 4. Remember the radius is 1 REMEMBER THE RATIOS OF A 45 -45 -90 TRIANGLE 1 45 -1 45

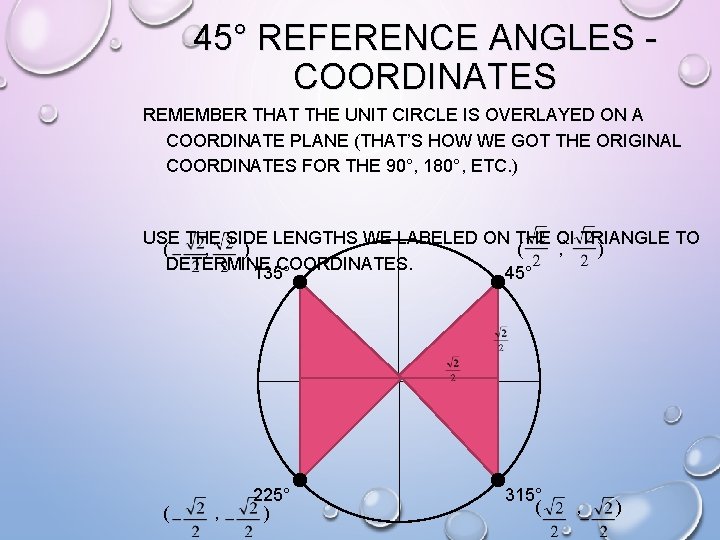
45° REFERENCE ANGLES - COORDINATES REMEMBER THAT THE UNIT CIRCLE IS OVERLAYED ON A COORDINATE PLANE (THAT’S HOW WE GOT THE ORIGINAL COORDINATES FOR THE 90°, 180°, ETC. ) USE THE SIDE LENGTHS WE LABELED ON THE QI TRIANGLE TO ( , ) DETERMINE COORDINATES. 135° 45° 225° ( , ) 315° ( , )

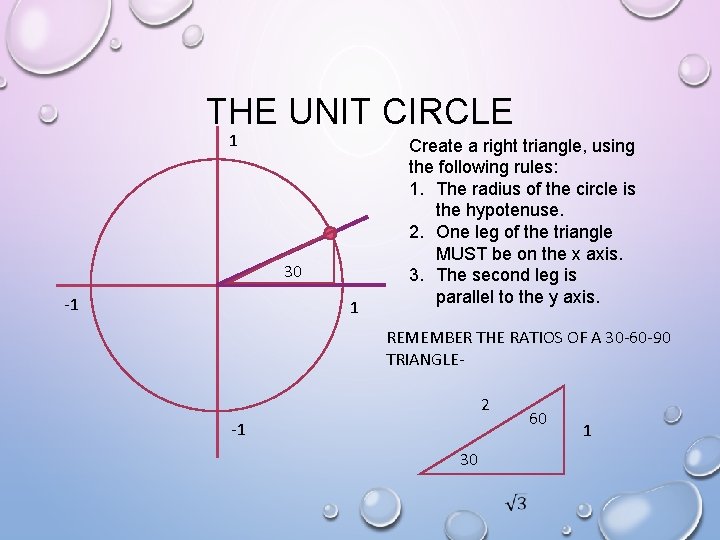
THE UNIT CIRCLE 1 30 -1 1 Create a right triangle, using the following rules: 1. The radius of the circle is the hypotenuse. 2. One leg of the triangle MUST be on the x axis. 3. The second leg is parallel to the y axis. REMEMBER THE RATIOS OF A 30 -60 -90 TRIANGLE 2 60 -1 30 1

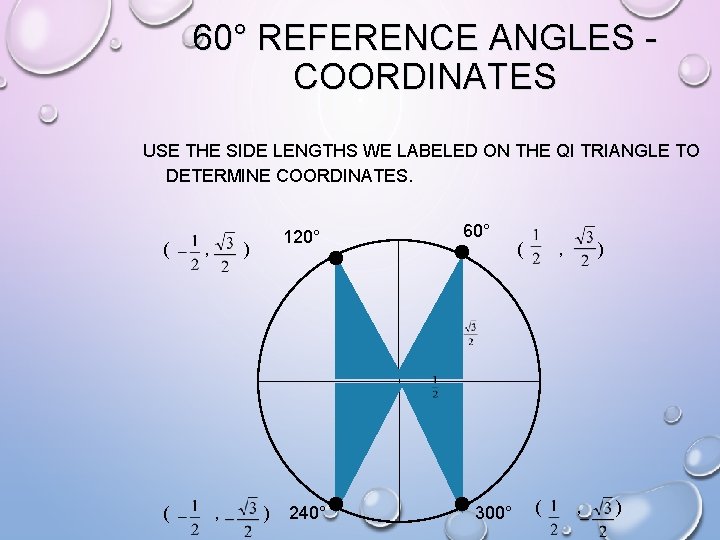
60° REFERENCE ANGLES - COORDINATES USE THE SIDE LENGTHS WE LABELED ON THE QI TRIANGLE TO DETERMINE COORDINATES. ( , ) ( , ) 120° 240° 60° 300° ( , )

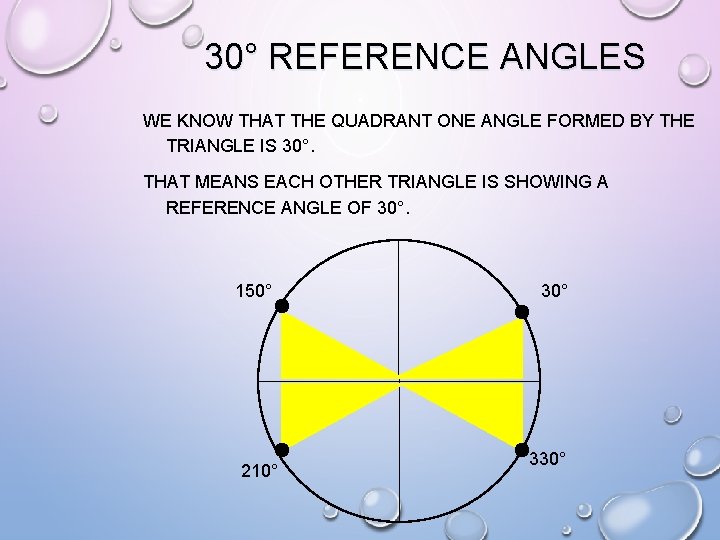
30° REFERENCE ANGLES WE KNOW THAT THE QUADRANT ONE ANGLE FORMED BY THE TRIANGLE IS 30°. THAT MEANS EACH OTHER TRIANGLE IS SHOWING A REFERENCE ANGLE OF 30°. 150° 210° 330°

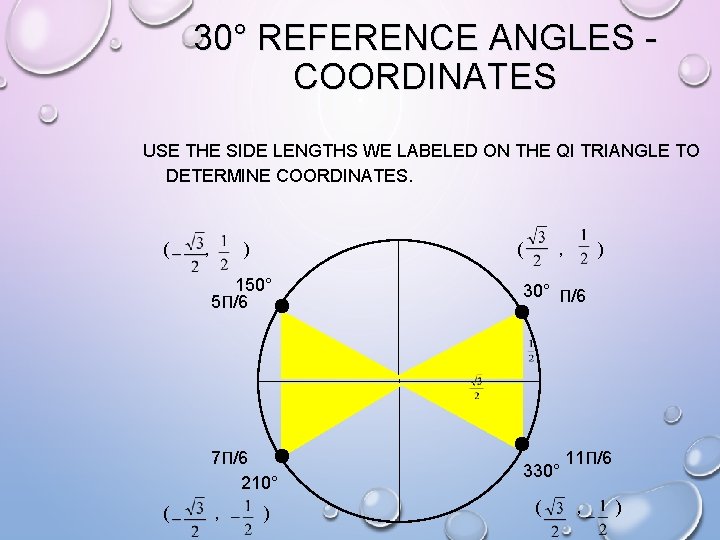
30° REFERENCE ANGLES - COORDINATES USE THE SIDE LENGTHS WE LABELED ON THE QI TRIANGLE TO DETERMINE COORDINATES. ( , ) 150° 5Π/6 30° Π/6 7Π/6 210° 330° ( , ) 11Π/6 ( , )

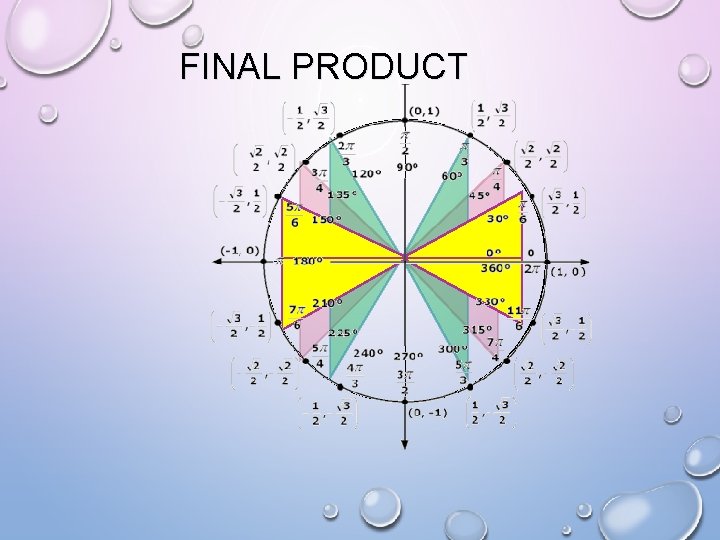
FINAL PRODUCT

THE UNIT CIRCLE