Angles and Determination of Direction Angle difference in

Angles and Determination of Direction ► Angle – difference in direction of 2 lines § Another way of explaining is the amount of rotation about a central point § 3 kinds of Horizontal angles: Exterior ( to right); Interior; Deflection § To turn an angle you need ► A reference line ► Direction of turning ► Angular distance § Angular Units ► Degrees, § § § minutes, seconds (sexagesimal system) Circle divided into 360 degrees Each degree divided by 60 minutes Each minute divided into 60 seconds ► Radians § 1 radian = 1/2 of a circle = 0. 1592*360 = 57 17’ 44. 8” ► Grads (Centesimal System) – now called Gon § 1/400 of a circle or 0 54’ 00” (100 gon = 90 )

Angles and Determination of Direction Angles turned in field must be accurate: 3 X least count is max. error ► Check #1 – Close horizon when turning ► If traverse closes: sum of the interior angles should equal the sum of ► § (N-2)X 180, N = Number of sides angles = (3 -2) 180 = 180 ► 4 angles = (4 -2) 180 = 360 ► 8 angles = (8 -2) 180 = 1080 ► 25 angles = (25 -2) 180 = 4140 ► 3 § If an exterior angle exists, subtract it from 360 to obtain the interior § Angular closure should be checked before leaving the field

Angles and Determination of Direction If angular adjustment does not divide out equally: ► 1. 2. 3. Do not go to decimal unless instrument reads to decimal Observe field notes for angles with poor closure or where problems turning angles existed. Apply excess to these angles evenly. If unable to view field notes or no apparent source, generally apply excess to angles with shortest sides Bearings/Azimuths ► § § Bearing of a line is the acute horizontal angle between a reference meridian (North and South) and a line Azimuth of a line is the horizontal angle measured from the North meridian clockwise to the line

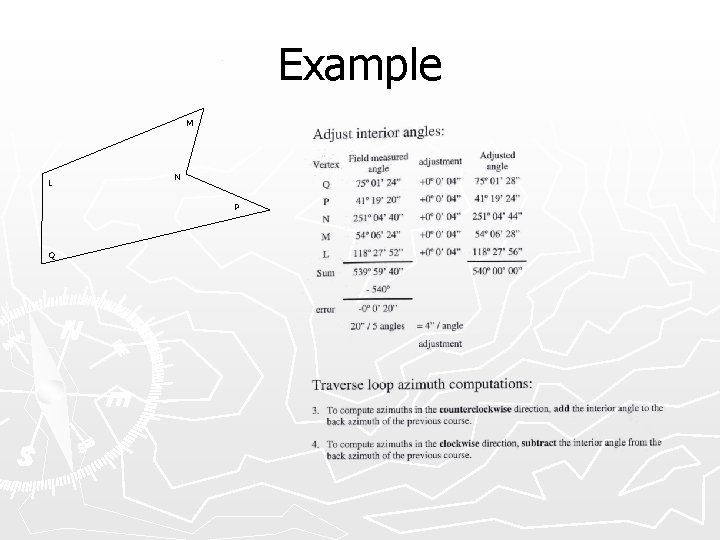
Example M L N P Q

Angles and Determination of Direction 4 Point Comparison Bearing Azimuth 1. Numeric Value 0 -90 0 -360 2. Method of Expressing 2 letters & number Number only 3. Direction Clockwise & counterclockwise Clockwise 4. Position of 0 point North and South North It is always very important to have your field sketch properly oriented

Angles and Determination of Direction Rectangular Coordinates Totally based on computation of right triangle North – South Movement = Latitude = D X cos A East – West Movement = Departure = D X sin A ► Latitude running North are +, South are – ► Departure running East are +, West are – ►

Angles and Determination of Direction ► Basic Procedure 1. 2. 3. 4. 5. Determine Latitude and Departure Sum Lat. and Departure to calc. closure Obtain balanced Lat. and Dept. (Compass Rule) Determine coordinates Once rectangular coordinates are known on point, their exact location is known with respect to all other points in the network

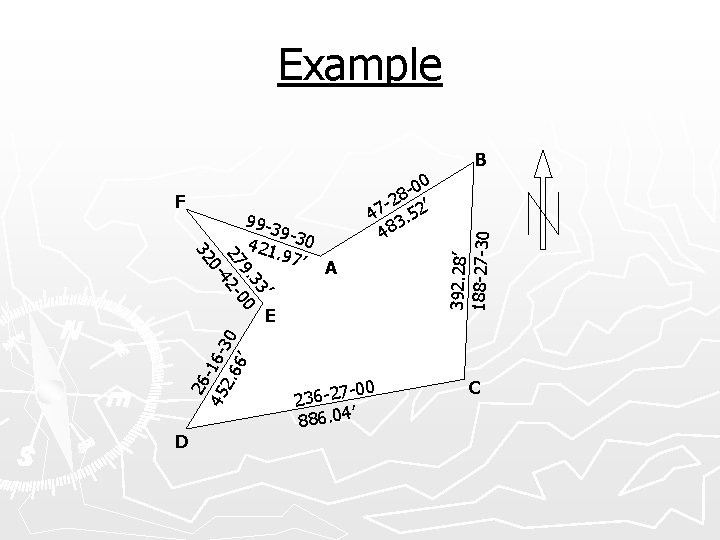
Example F ’ 33 9. 0 27 42 -0 0 - 32 99 -3 9 421 -30. 97’ A -00 8 -2 2’ 7 4 3. 5 48 26 45 -16 -3 2. 6 0 6’ E D -00 236 -27 ’ 886. 04 392. 28’ 188 -27 -30 B C

Angles and Determination of Direction ► Balancing Methods 1. Compass Rule: (Bowditch) Used when accuracy of and length measurement is equal ► ► 2. Transit Rule: Used if angles are more accurate than distances (more accurate direction) ► ► 3. 4. (Error Lat. /Perimeter length) X Distance = Latitude Correction (Error Dept. /Perimeter length) X Distance = Departure Correction Latitude (Side) = (Lat. Side/Sum all Lat. ) X Lat. error Correction Departure (Side) = (Dept. Side/Sum all Dept. ) X Dept. error Crandall Method: Used when larger random error exists in linear measurements that angular. Directional adjustments from balancing are held fixed and distances are balanced by a weighted least squares procedure Least Squares: Based on theory of probability. Angular and linear adjustments are made simultaneously. Hand methods are long and complex not often done. Computer adjustment through existing software make it feasible, which is why it is often used today

Area, Inverse, Intersection ► Once rectangular coordinates are established on all points, the relationship to all other points is known. You can: 1. Determine area of all or any portion 2. Determine length and direction between any 2 points 3. Locate new points by intersection

Area, Inverse, Intersection ► Area: Method is area by cross multiplication Using example from traverse lecture: NA X EB + NB X EC + NC X ED + ND X EE + NE X EF + NF X EA = Sum N EA X NB + EB X NC + EC X ND + ED X NE + EE X NF + EF X NA = Sum E A 10000 5000. 0000 B 10326. 7981 5356. 3614 C 9938. 7277 5298. 7122 D 9448. 9156 4560. 3990 E 9854. 7405 4760. 8417 F 10070. 8565 4583. 9559 A 10000 5000. 0000 Difference in Sums/2 = Square feet/43560 = Acres Sum N = 294, 119, 678. 8 Sum E = 293, 663, 353. 6 456, 325. 2 / 2 = 228, 162. 6 ft 2 = 5. 24 Ac

Area, Inverse, Intersection Example: Determine Area of A, D, E, F, A A 10000 5000. 0000 D 9448. 9156 4560. 3990 E 9854. 7405 4760. 8417 F 10070. 8565 4583. 9559 A 10000 5000. 0000 N = 186, 116, 759. 8 E = 185, 971, 439. 3 145, 320. 5 / 2 = 72, 660. 25 ft 2 = 1. 67 Ac

Area, Inverse, Intersection ► Inverse: With known coordinates of any two points on a system, you find the distance and direction between the two C D ► 9938. 7277 9448. 9156 489. 8121 5298. 7122 4560. 3990 738. 3132 To find the Inverse between 2 Points 1. Find difference in N & E of coordinates 2. Plot 3. 4. 5. 6. ► ► Use point you are going from 1 st Plot longest side 1 st Determine length using Pythagorean (a 2 + b 2 = c 2) Determine reference direction Determine local using tan A = a/b Determine line direction

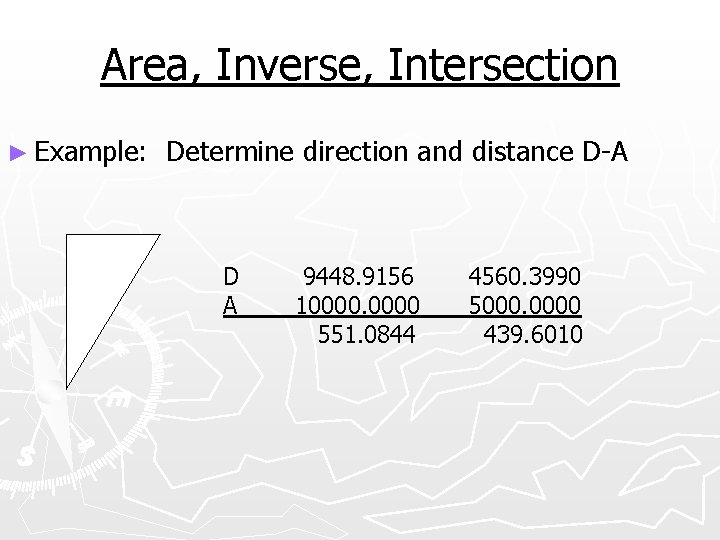
Area, Inverse, Intersection ► Example: Determine direction and distance D-A D A 9448. 9156 10000 551. 0844 4560. 3990 5000. 0000 439. 6010

Area, Inverse, Intersection ► Intersection: Determination of unknown point location with directions from two points known 1. Determine difference in coordinates Plot points and line projections Set up dual formulas (as Latitude and Departure) Solve for length Compute coordinate as sideshot 2. 3. 4. 5. C D 9938. 7277 9448. 9156 489. 8121 5298. 7122 4560. 3990 738. 3132

Area, Inverse, Intersection ► Example: What are the coordinates of the point of intersection of line C-F and D-A. Azimuth D-A = 38 34’ 46”. Coordinates of D: N = 9448. 9156, E = 4560. 3990 C F 9938. 7277 10070. 8565 132. 1288 5298. 7122 4583. 9559 714. 7563