Angledomain parameters computed via weighted slantstack Angle stacks

Angle-domain parameters computed via weighted slant-stack Angle stacks Claudio Guerra SEP-131, p. 59

Motivation • Post migration processes in the reflection-angle domain – – migration-velocity analysis residual multiple attenuation AVA regularization of the least-squares inverse imaging • Compensate for illumination problems in ADCIGs

Outline • • Introduction Weighted OFF 2 ANG Results Conclusions

Introduction • SEP 125 - Valenciano and Biondi – Compute the Hessian in the angle domain by chaining operators T*, H and T. S(m) = ½||Lmh – dobs||2 = ½||LTmg – dobs||2 2 S(m)/ m 2 = T*L*LT H(x, g; x’, g’) = T*(g, h) H(x, h; x’, h’) T(g, h) H(x, g; x’, g’) – angle-domain Hessian mg – ADCIG T(g, h) – angle-to-offset transformation L – modeling operator H(x, h; x’, h’) – offset-domain Hessian mh – SODCIG T*(g, h) – offset-to-angle transformation L* - migration

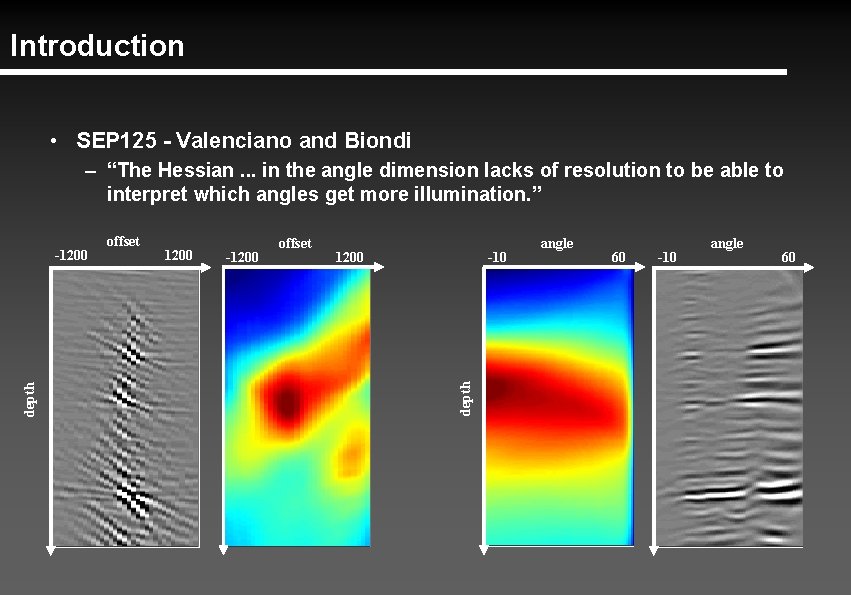
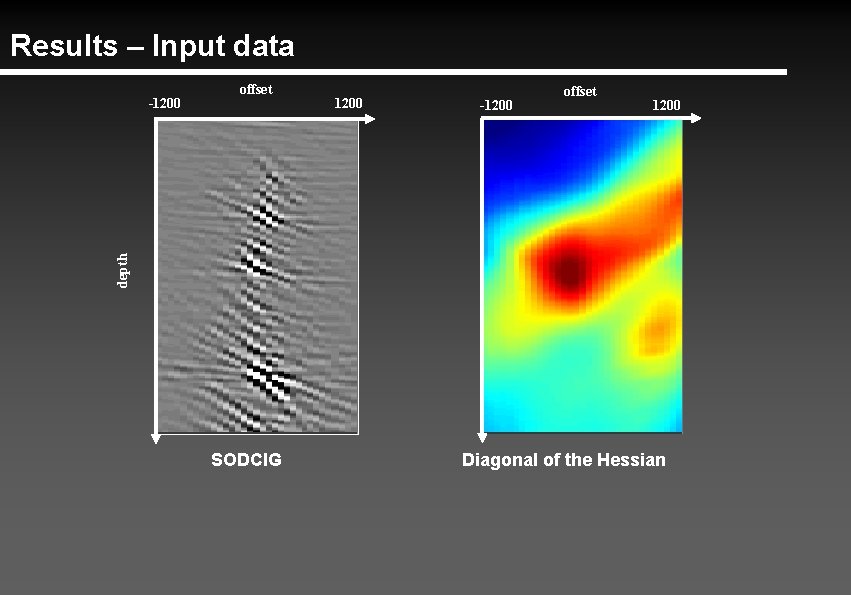
Introduction • SEP 125 - Valenciano and Biondi – “The Hessian. . . in the angle dimension lacks of resolution to be able to interpret which angles get more illumination. ” 1200 -1200 offset 1200 -10 depth -1200 offset angle 60 -10 angle 60

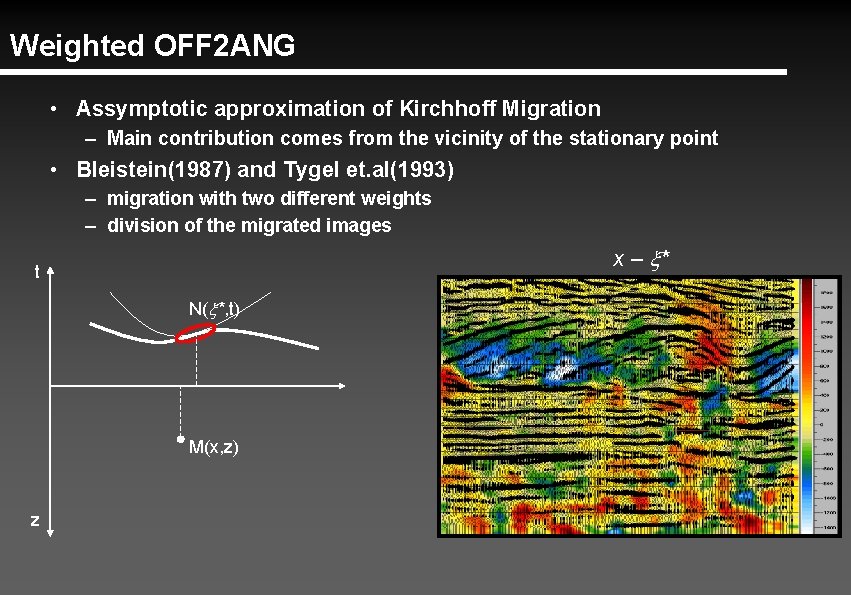
Weighted OFF 2 ANG • Assymptotic approximation of Kirchhoff Migration – Main contribution comes from the vicinity of the stationary point • Bleistein(1987) and Tygel et. al(1993) – migration with two different weights – division of the migrated images x – x* t N(x*, t) M(x, z) z

Weighted OFF 2 ANG – phase behavior Slant – stack Q – ADCIG f (z) – wavelet h – subsurface offset P – SODCIG zr – reflector g – reflection angle z – stacking line A – amplitude – rho filter

Weighted OFF 2 ANG – phase behavior Slant – stack Q – ADCIG f (z) – wavelet h* – stationary offset F – phase function A – amplitude g – reflection angle

Weighted OFF 2 ANG Weighted Slant – stack – ADCIG f (z) – wavelet h* – stationary offset F – phase function A – amplitude g – reflection angle

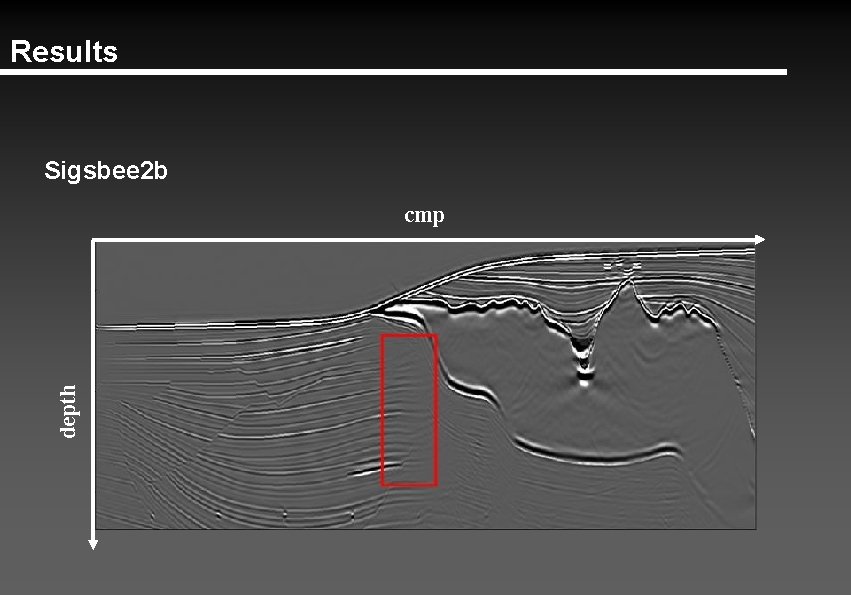
Results Sigsbee 2 b depth cmp

Results – Input data 1200 -1200 offset 1200 depth -1200 offset SODCIG Diagonal of the Hessian

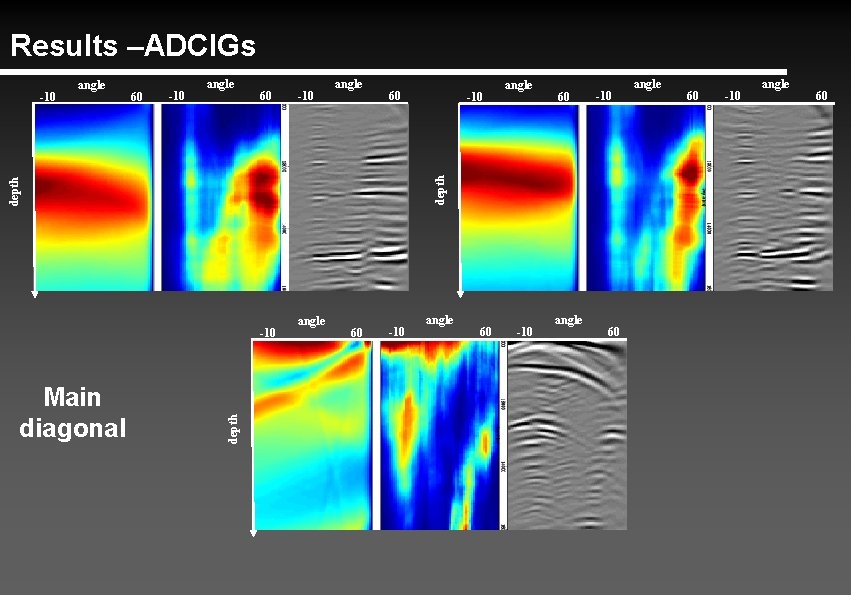
Results –ADCIGs 60 -10 angle 60 depth -10 Main diagonal -10 angle 60 -10 depth angle depth -10 angle 60 -10 angle 60

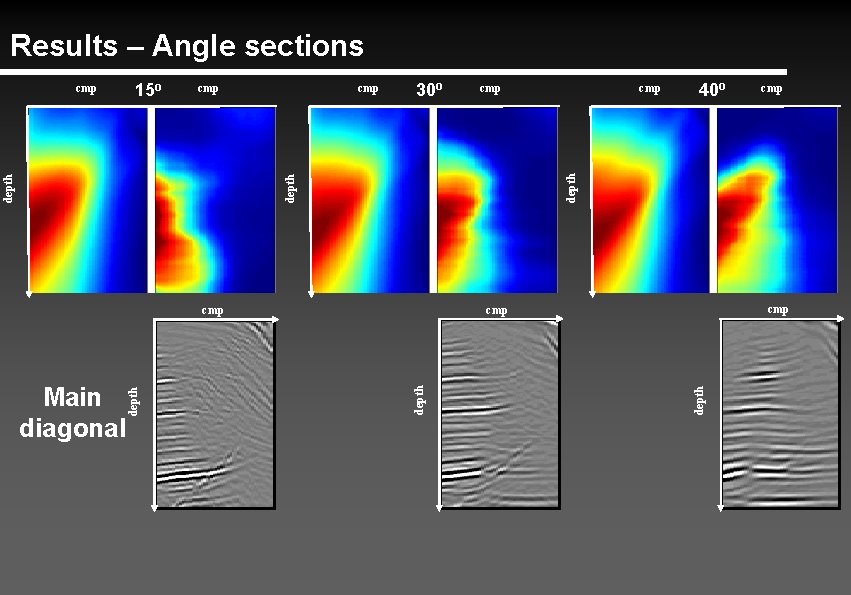
Results – Angle sections 30 o depth 40 o cmp cmp depth cmp Main diagonal cmp cmp depth 15 o depth cmp

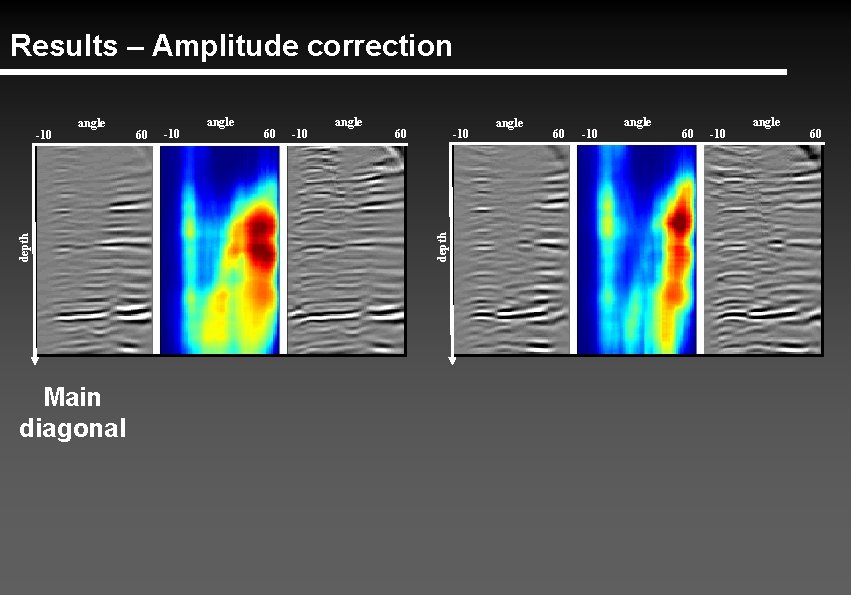
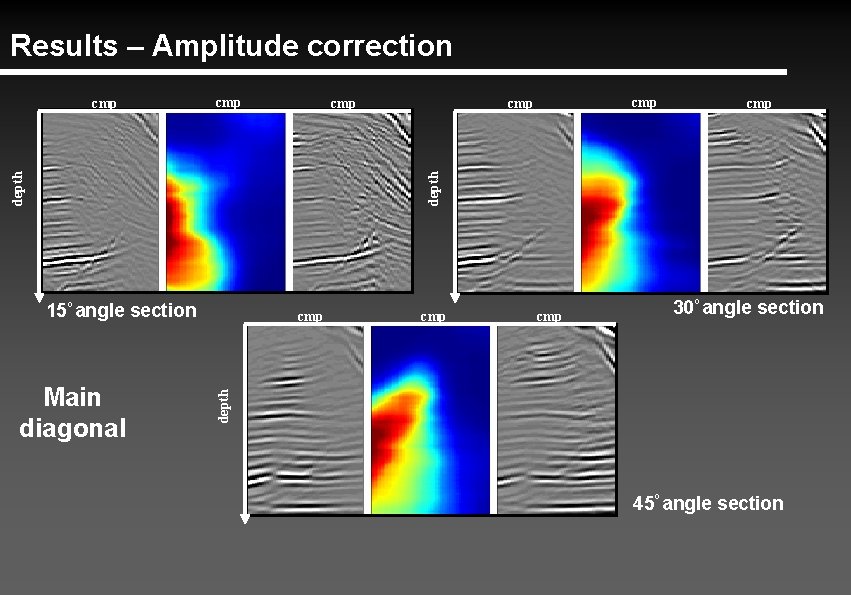
Results – Amplitude correction Main diagonal 60 -10 angle 60 -10 depth angle depth -10 angle 60

Results – Amplitude correction cmp cmp cmp depth cmp 15º angle section cmp 30º angle section depth Main diagonal cmp 45º angle section

Results – Amplitude correction Angle stack depth cmp

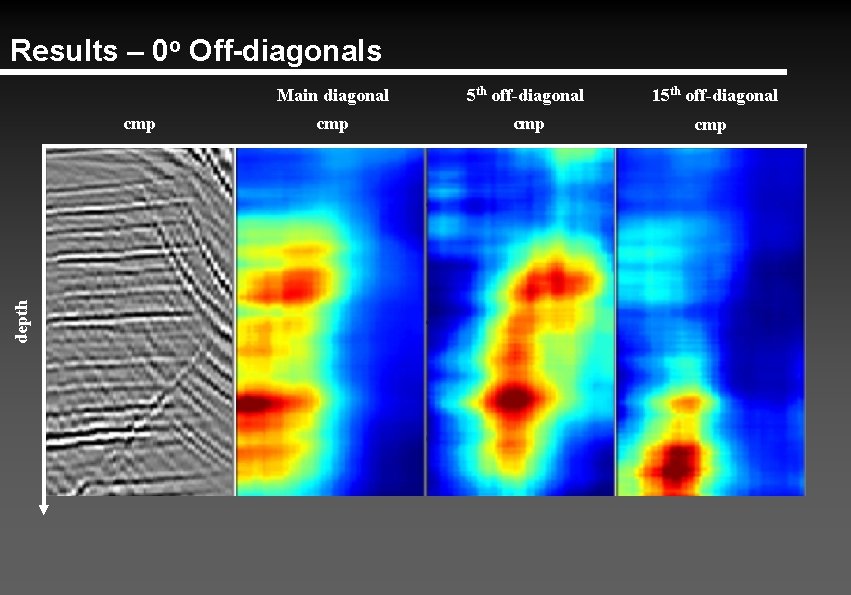
Results – 0 o Off-diagonals depth cmp Main diagonal 5 th off-diagonal 15 th off-diagonal cmp cmp

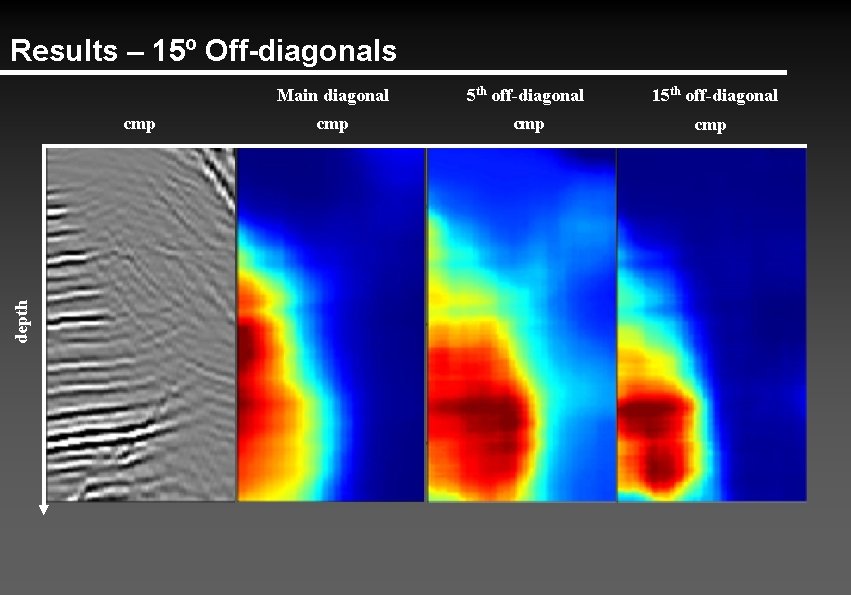
Results – 15º Off-diagonals depth cmp Main diagonal 5 th off-diagonal 15 th off-diagonal cmp cmp

Conclusions • Alternative approach to transform the Hessian to the angle domain • Well balanced ADCIGs – Better angle-stack • Off-diagonal terms – Still no direct application