Angledomain Common Image Gathers for Anisotropic Migration Biondo

Angle-domain Common Image Gathers for Anisotropic Migration Biondo Biondi SEP 123 - pp. 1 -49 SEP meeting March 8, 2006 biondo@stanford. edu

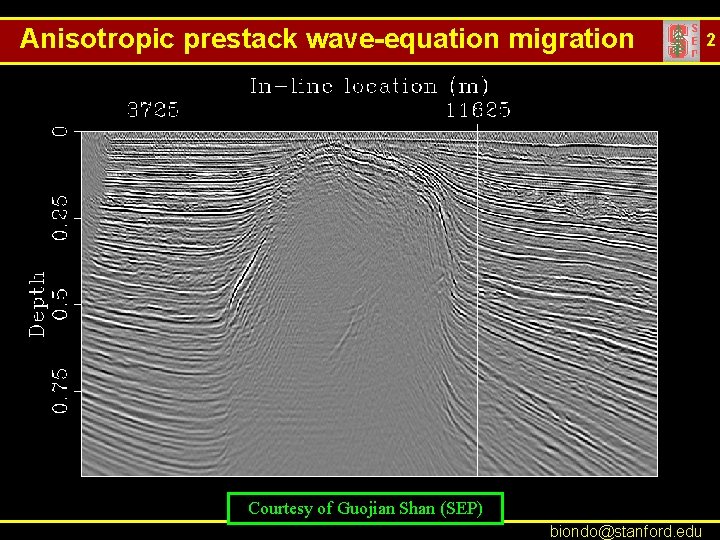
Anisotropic prestack wave-equation migration Courtesy of Guojian Shan (SEP) biondo@stanford. edu 2

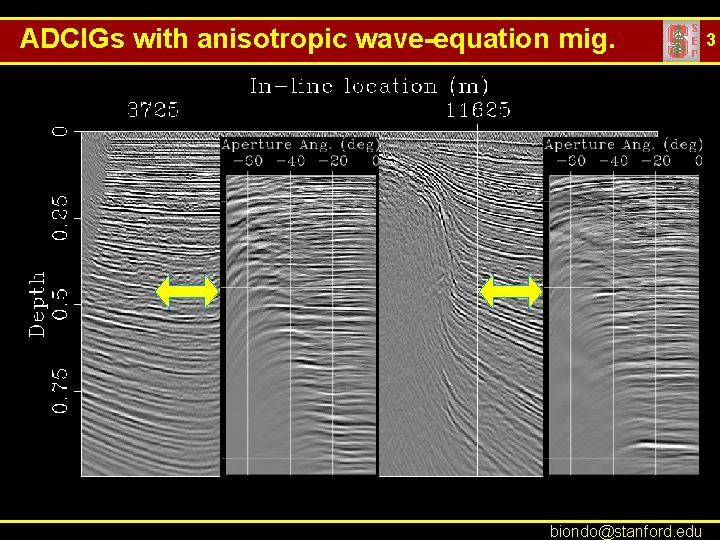
ADCIGs with anisotropic wave-equation mig. biondo@stanford. edu 3

Outline 4 v Computation of Angle-Domain CIGs (ADCIGs) with anisotropic migration l Phase l Dip or group angles? independent? v Analysis of Residual Moveout (RMO) caused by perturbations in anisotropic-velocity parameters l Phase or group angles? l Phase or group velocity? biondo@stanford. edu

Outline 5 v Computation of Angle-Domain CIGs (ADCIGs) with anisotropic migration l Phase l Dip or group angles? independent? v Analysis of Residual Moveout (RMO) caused by perturbations in anisotropic-velocity parameters l Phase or group angles? l Phase or group velocity? biondo@stanford. edu

ADCIGs from isotropic wavefield migration • Offset-domain CIGs (Rickett and Sava, 2001) • Angle-domain CIGs (Sava and Fomel, 2003) biondo@stanford. edu 6

ADCIGs from anisotropic wavefield migration • Offset-domain CIGs (Rickett and Sava, 2001) • Angle-domain CIGs (Sava and Fomel, 2003) ? biondo@stanford. edu 7

Dipping reflectors 8 • The transformation to angle domain becomes dip-dependent and local-velocity dependent biondo@stanford. edu

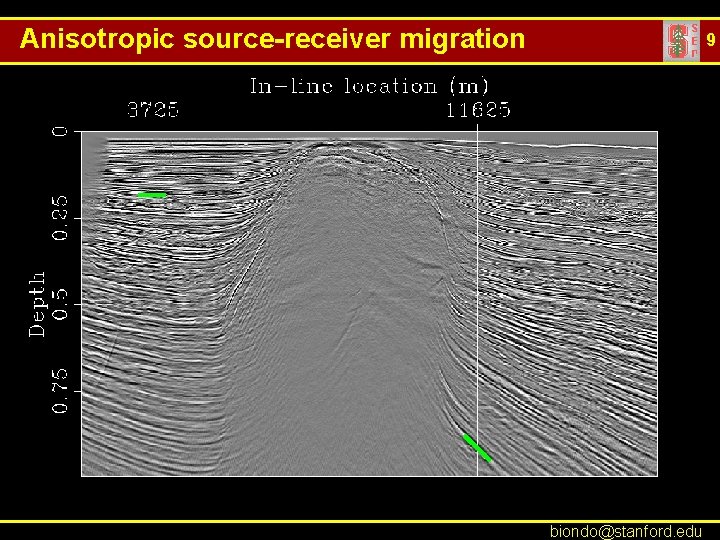
Anisotropic source-receiver migration 9 biondo@stanford. edu

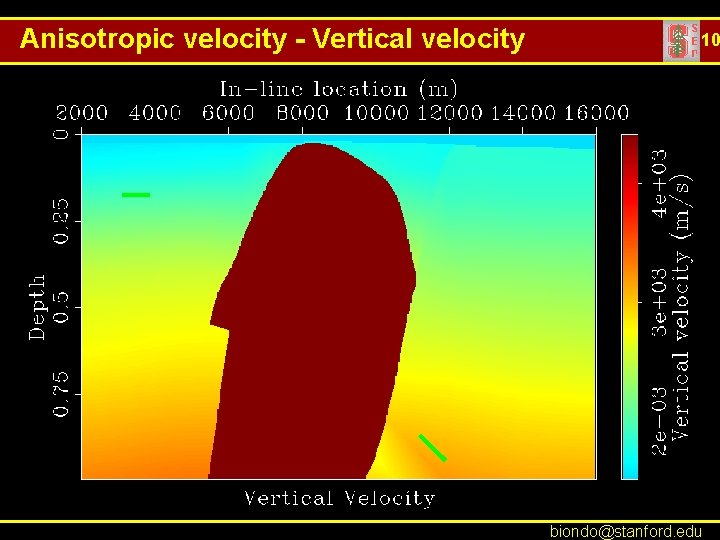
Anisotropic velocity - Vertical velocity 10 biondo@stanford. edu

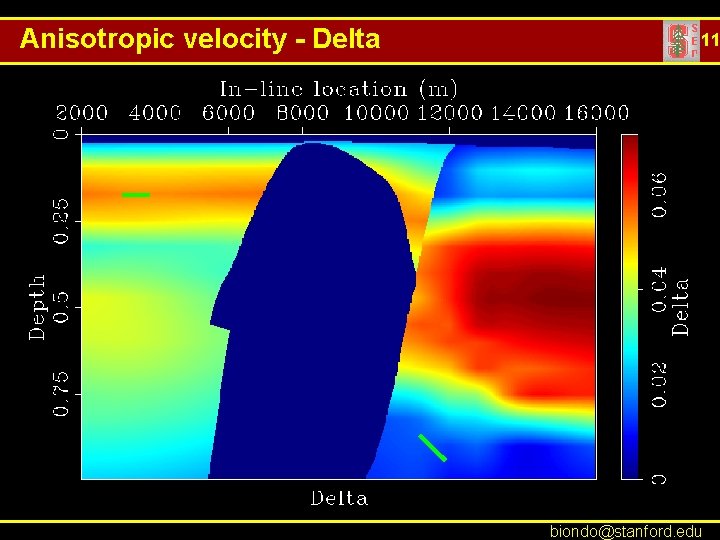
Anisotropic velocity - Delta 11 biondo@stanford. edu

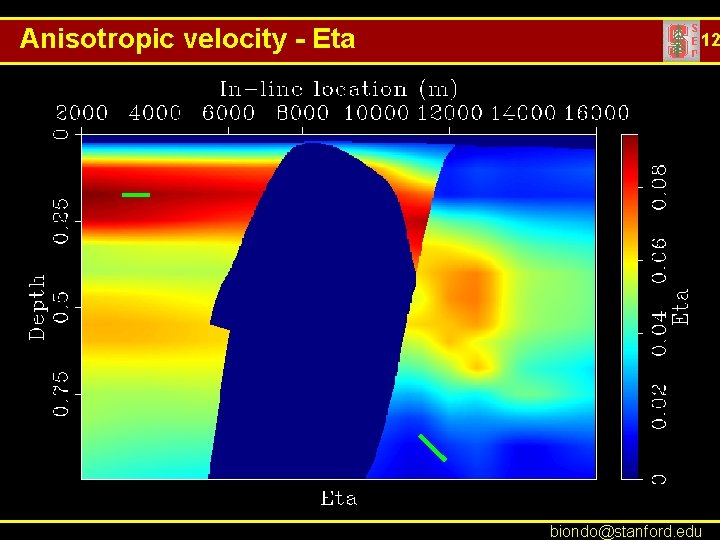
Anisotropic velocity - Eta 12 biondo@stanford. edu

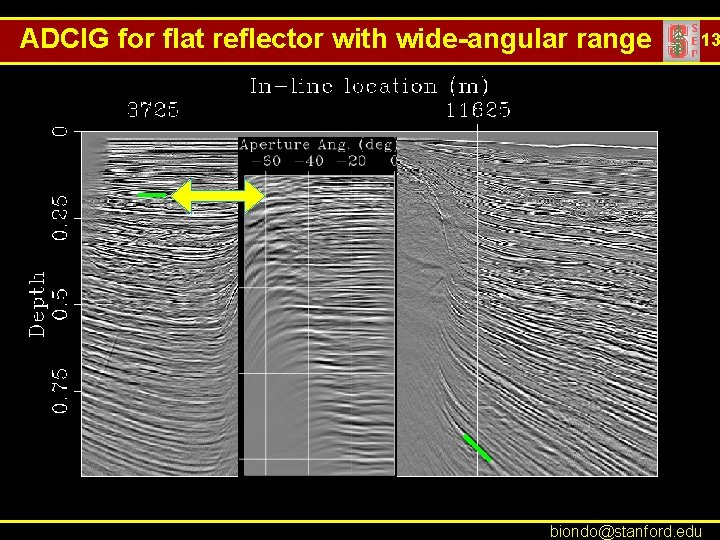
ADCIG for flat reflector with wide-angular range 13 biondo@stanford. edu

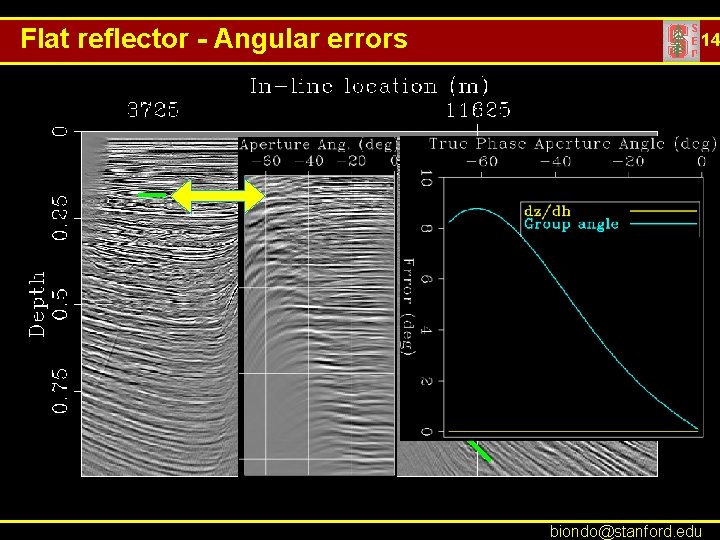
Flat reflector - Angular errors 14 biondo@stanford. edu

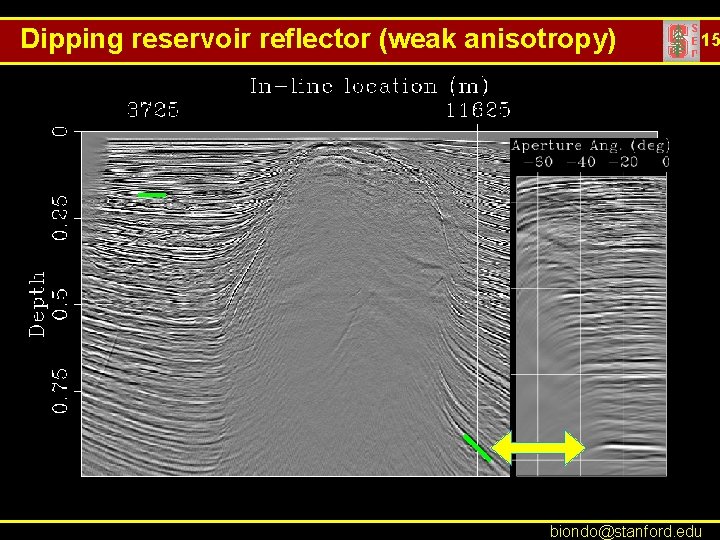
Dipping reservoir reflector (weak anisotropy) 15 biondo@stanford. edu

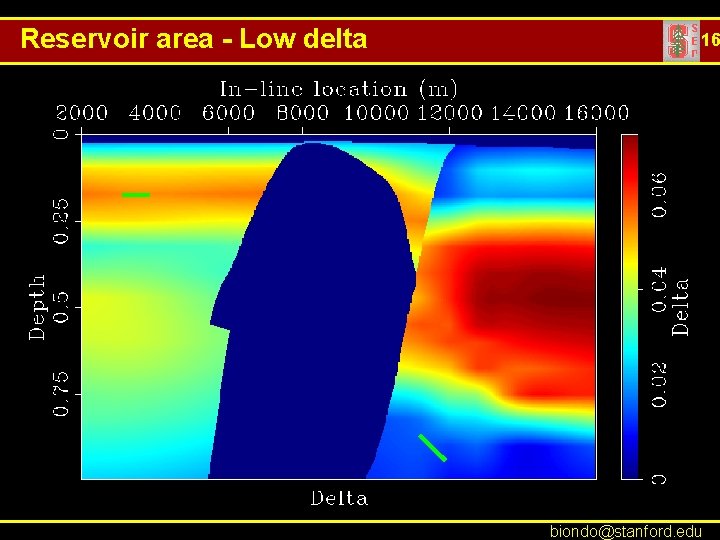
Reservoir area - Low delta 16 biondo@stanford. edu

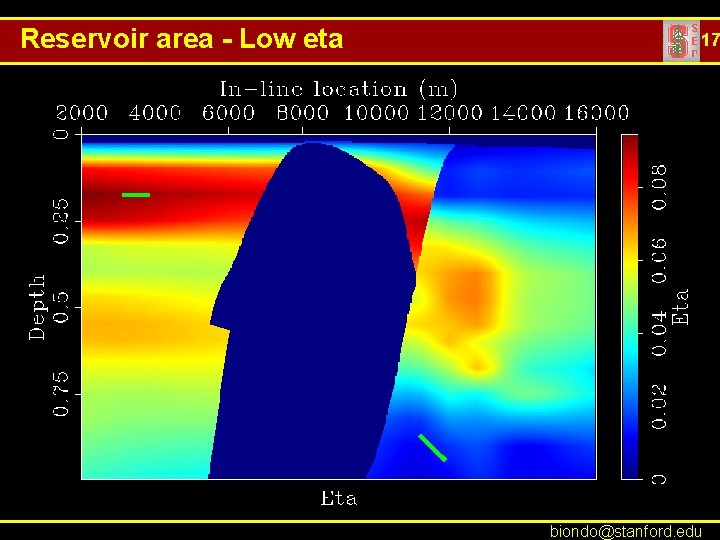
Reservoir area - Low eta 17 biondo@stanford. edu

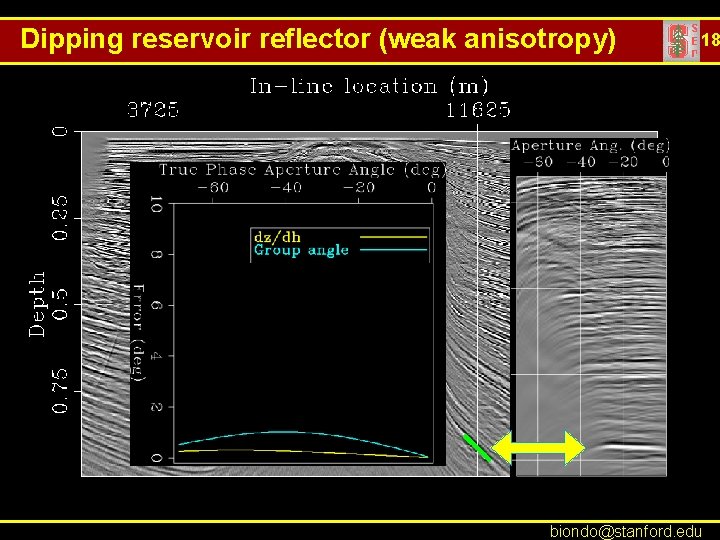
Dipping reservoir reflector (weak anisotropy) 18 biondo@stanford. edu

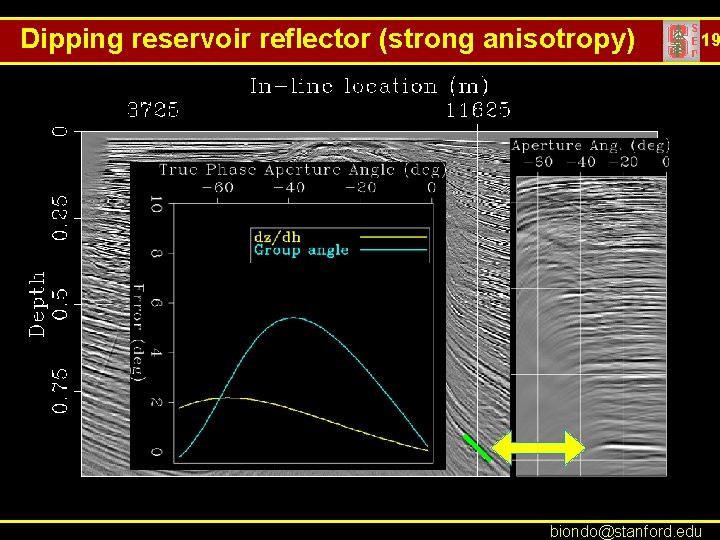
Dipping reservoir reflector (strong anisotropy) 19 biondo@stanford. edu

Outline 20 v Computation of Angle-Domain CIGs (ADCIGs) with anisotropic migration l Phase l Dip or group angles? independent? v Analysis of Residual Moveout (RMO) caused by perturbations in anisotropic-velocity parameters l Phase or group angles? l Phase or group velocity? biondo@stanford. edu

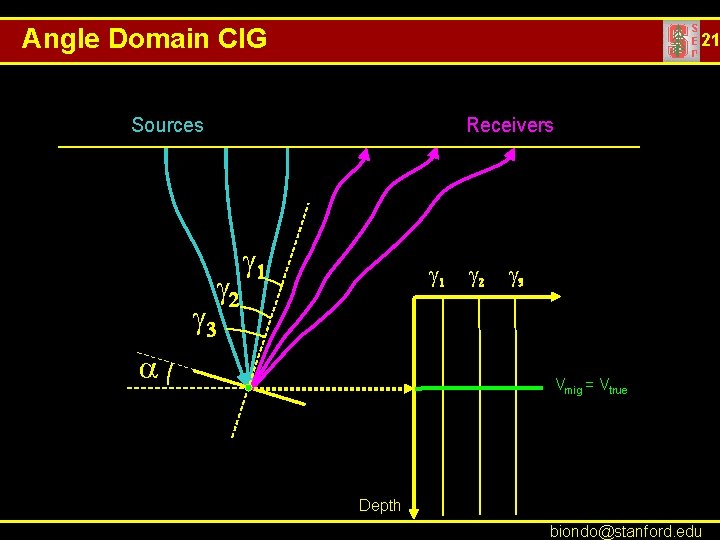
Angle Domain CIG 21 Sources Receivers g 2 g 1 g 2 g 3 a Vmig = Vtrue Depth biondo@stanford. edu

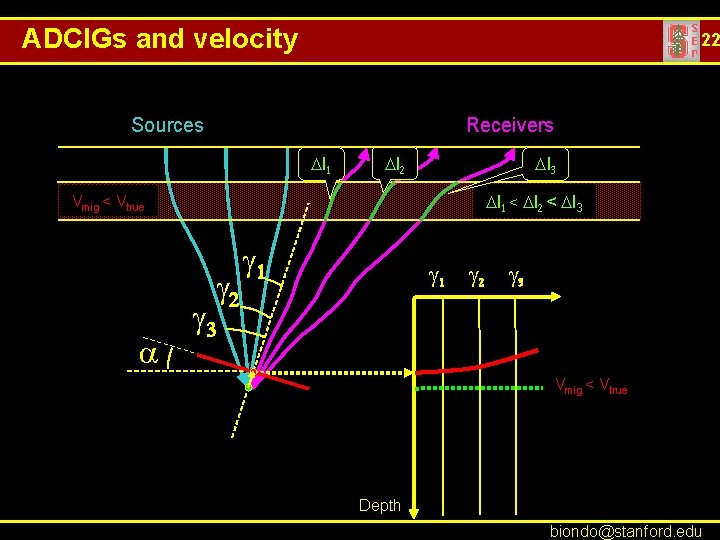
ADCIGs and velocity 22 Sources Receivers Dl 1 Dl 2 Dl 3 Dl 1 < Dl 2 < Dl 3 Vmig < Vtrue g 2 a g 1 g 2 g 3 Vmig < Vtrue Depth biondo@stanford. edu

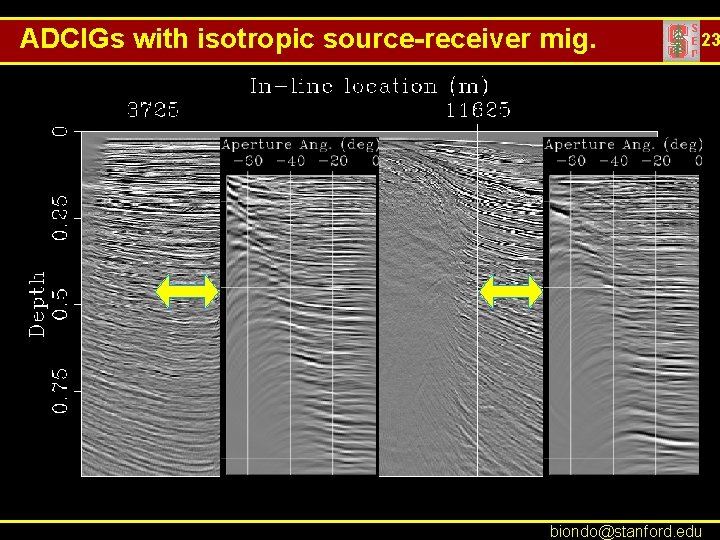
ADCIGs with isotropic source-receiver mig. 23 biondo@stanford. edu

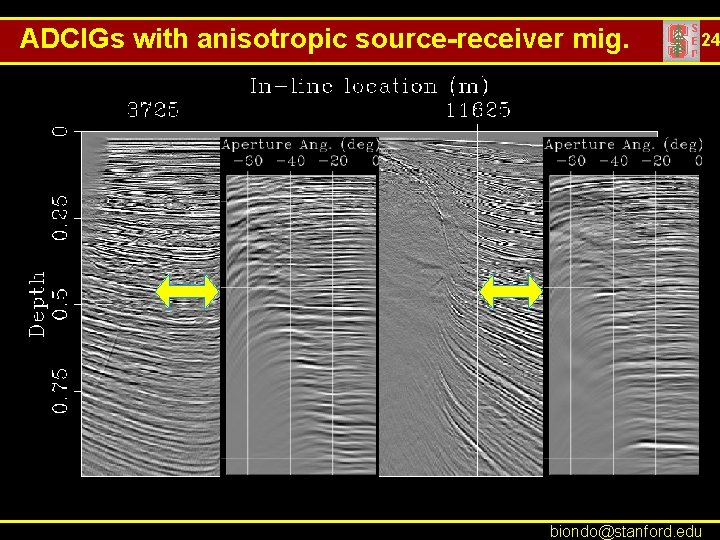
ADCIGs with anisotropic source-receiver mig. 24 biondo@stanford. edu

Residual Moveout with velocity scaling 25 • Uniform scaling of velocity • Arbitrary scaling of velocity biondo@stanford. edu

Residual Moveout functions for flat reflectors 26 • Isotropic Residual Moveout (RMO) (Biondi and Symes, 2004) • Anisotropic Residual Moveout (RMO) biondo@stanford. edu

RMO functions for arbitrary perturbations 27 • RMO for perturbations in VV, VH, VN biondo@stanford. edu

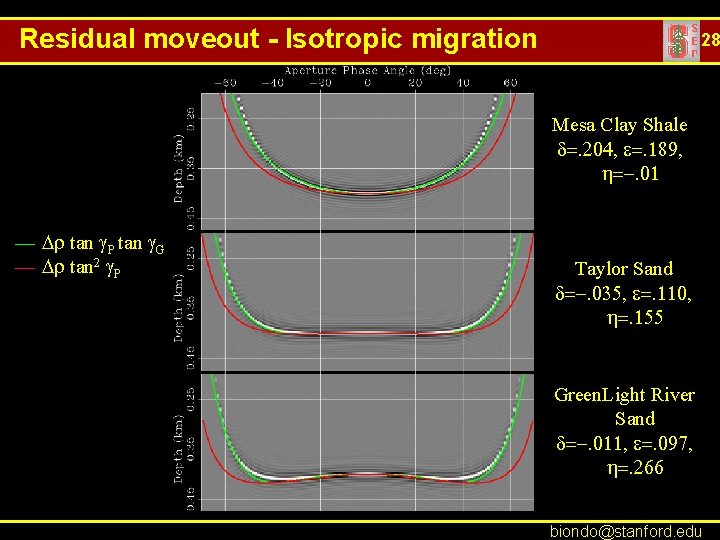
Residual moveout - Isotropic migration 28 Mesa Clay Shale d=. 204, e=. 189, h=-. 01 — Dr tan g. P tan g. G — Dr tan 2 g. P Taylor Sand d=-. 035, e=. 110, h=. 155 Green. Light River Sand d=-. 011, e=. 097, h=. 266 biondo@stanford. edu

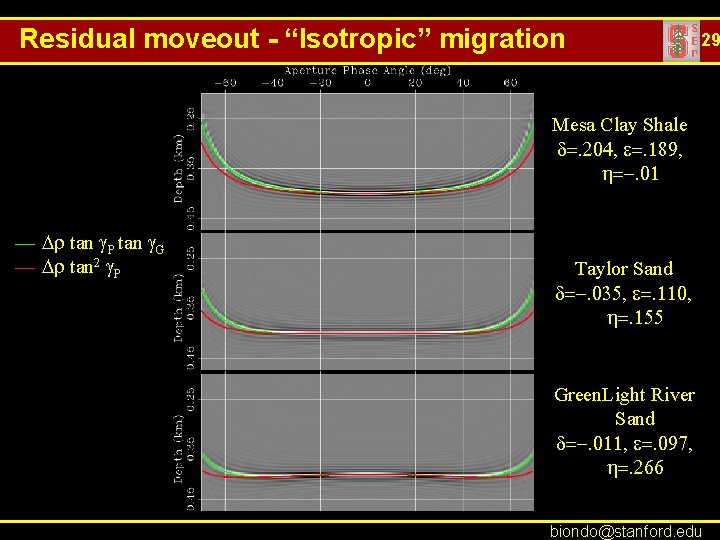
Residual moveout - “Isotropic” migration 29 Mesa Clay Shale d=. 204, e=. 189, h=-. 01 — Dr tan g. P tan g. G — Dr tan 2 g. P Taylor Sand d=-. 035, e=. 110, h=. 155 Green. Light River Sand d=-. 011, e=. 097, h=. 266 biondo@stanford. edu

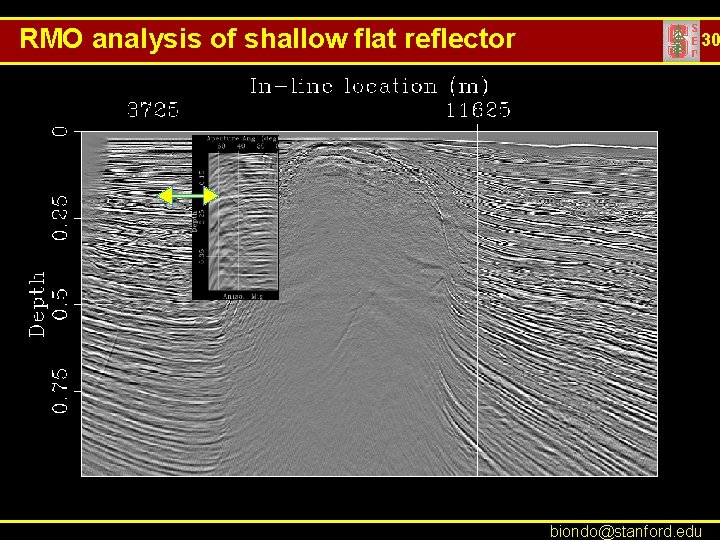
RMO analysis of shallow flat reflector 30 biondo@stanford. edu

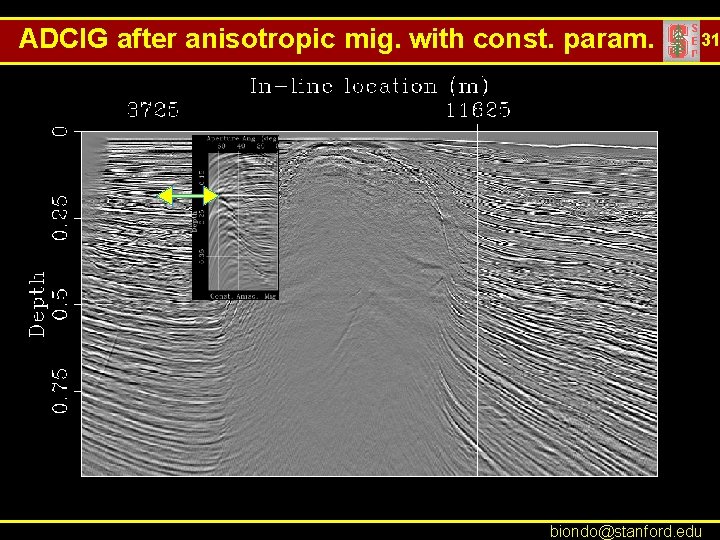
ADCIG after anisotropic mig. with const. param. 31 biondo@stanford. edu

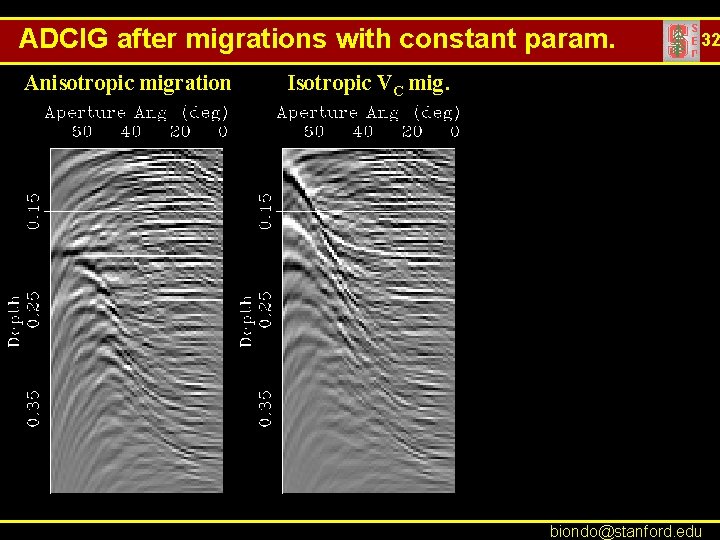
ADCIG after migrations with constant param. Anisotropic migration 32 Isotropic VC mig. biondo@stanford. edu

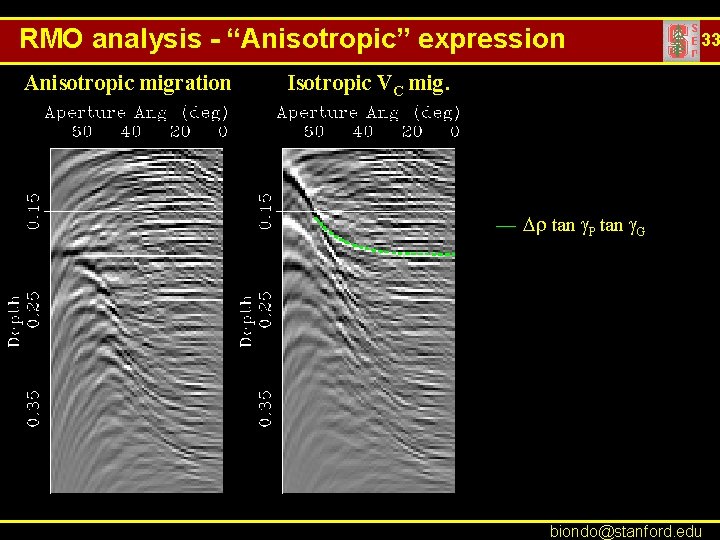
RMO analysis - “Anisotropic” expression Anisotropic migration 33 Isotropic VC mig. — Dr tan g. P tan g. G — Dr tan 2 g. P biondo@stanford. edu

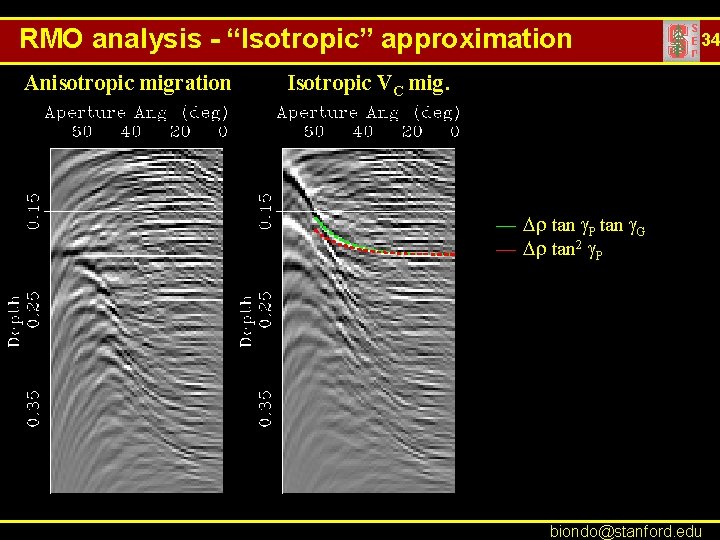
RMO analysis - “Isotropic” approximation Anisotropic migration 34 Isotropic VC mig. — Dr tan g. P tan g. G — Dr tan 2 g. P biondo@stanford. edu

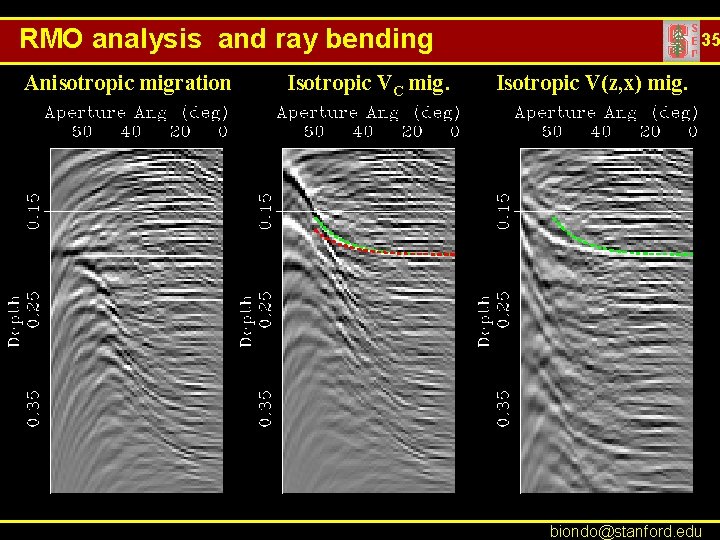
RMO analysis and ray bending Anisotropic migration Isotropic VC mig. 35 Isotropic V(z, x) mig. biondo@stanford. edu

Conclusions 36 • ADCIGs computed after anisotropic migration are functions of the phase angles. biondo@stanford. edu

Conclusions 37 • ADCIGs computed after anisotropic migration are functions of the phase angles. • For dipping reflectors, the relationship between subsurface-offset slopes (dz/dh) and phase angles is function of the dip and local slowness function, but this dependency is mild and could be ignored in practice. biondo@stanford. edu

Conclusions 38 • ADCIGs computed after anisotropic migration are functions of the phase angles. • For dipping reflectors, the relationship between subsurface-offset slopes (dz/dh) and phase angles is function of the dip and local slowness function, but this dependency is mild and could be ignored in practice. • First-order analysis of the RMO as a function of velocity perturbations yield relationships that accurately predict the actual RMO measured after migration on both synthetic and real data. biondo@stanford. edu

Acknowledgments 39 v. Exxon. Mobil, Joe Reilly and Jerry Krebs for GOM anisotropic data set and velocity model. biondo@stanford. edu

40 biondo@stanford. edu

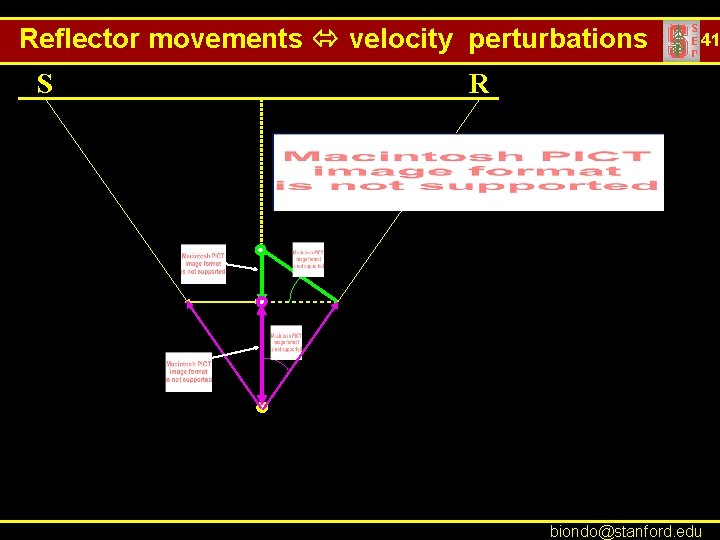
Reflector movements velocity perturbations S 41 R biondo@stanford. edu