Angle Properties www mathsrevision com Nat 5 Revision

Angle Properties www. mathsrevision. com Nat 5 Revision of Basic Angle Properties Isosceles Triangles in Circles Angles in a semi-circle Tangent line on a circle Interior / Exterior Angles in Polygon Exam Questions Friday, September 17, 2021 Created by Mr Lafferty 1

Revision Angle Properties www. mathsrevision. com Nat 5 Learning Intention Success Criteria 1. We are revising all the basic properties in Level 3 and 4. 1. To know the basic properties for angles. 2. Solve problems using properties. 17 -Sep-21 Created by Mr. Lafferty

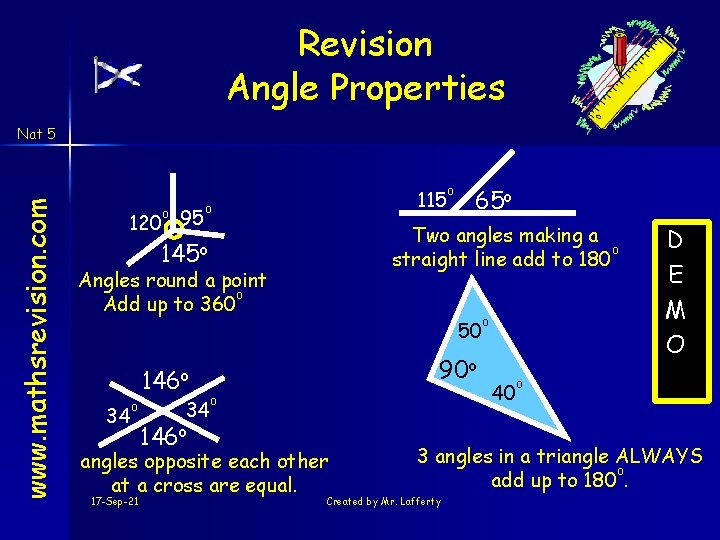
Revision Angle Properties www. mathsrevision. com Nat 5 o 120 95 115 o Angles round a point o Add up to 360 34 o 34 146 o 50 90 o o angles opposite each other at a cross are equal. 17 -Sep-21 65 o Two angles making a o straight line add to 180 145 o 146 o o o 40 D E M O o 3 angles in a triangle ALWAYS o add up to 180. Created by Mr. Lafferty

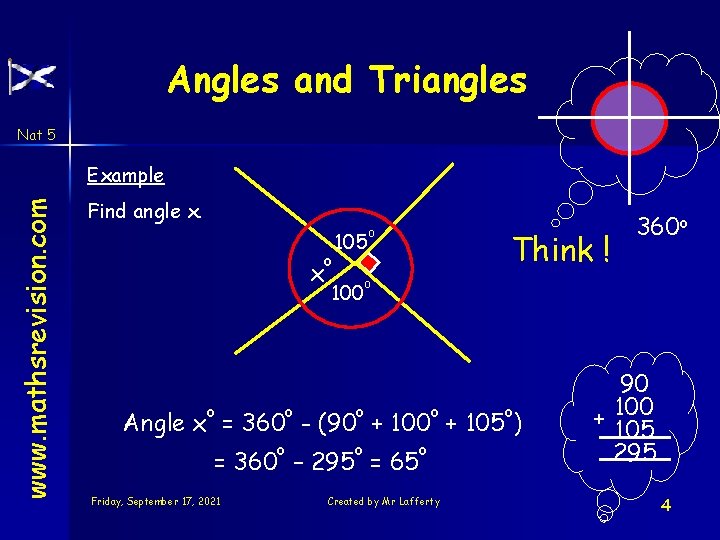
Angles and Triangles Nat 5 www. mathsrevision. com Example Find angle x. x o o o 105 100 o Think ! o o Angle x = 360 - (90 + 105 ) o o = 360 – 295 = 65 Friday, September 17, 2021 360 o o Created by Mr Lafferty 90 + 100 105 295 4

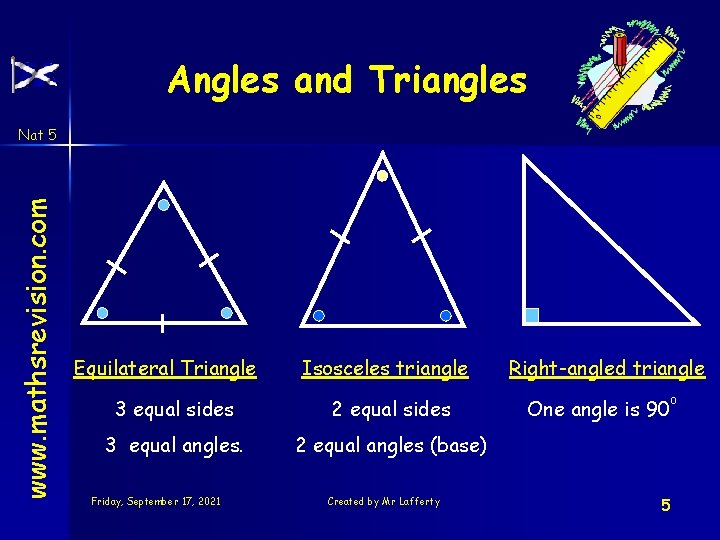
Angles and Triangles www. mathsrevision. com Nat 5 Equilateral Triangle Isosceles triangle 3 equal sides 2 equal sides 3 equal angles. 2 equal angles (base) Friday, September 17, 2021 Created by Mr Lafferty Right-angled triangle One angle is 90 o 5

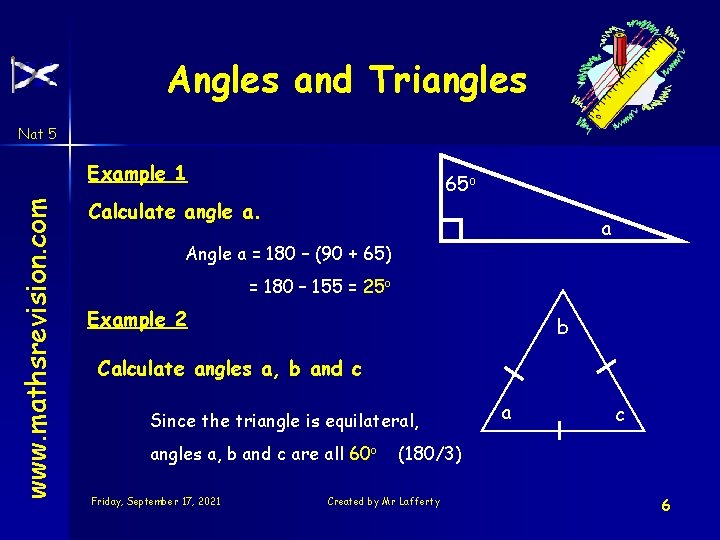
Angles and Triangles Nat 5 www. mathsrevision. com Example 1 65 o Calculate angle a. a Angle a = 180 – (90 + 65) = 180 – 155 = 25 o Example 2 b Calculate angles a, b and c Since the triangle is equilateral, angles a, b and c are all 60 o Friday, September 17, 2021 a c (180/3) Created by Mr Lafferty 6

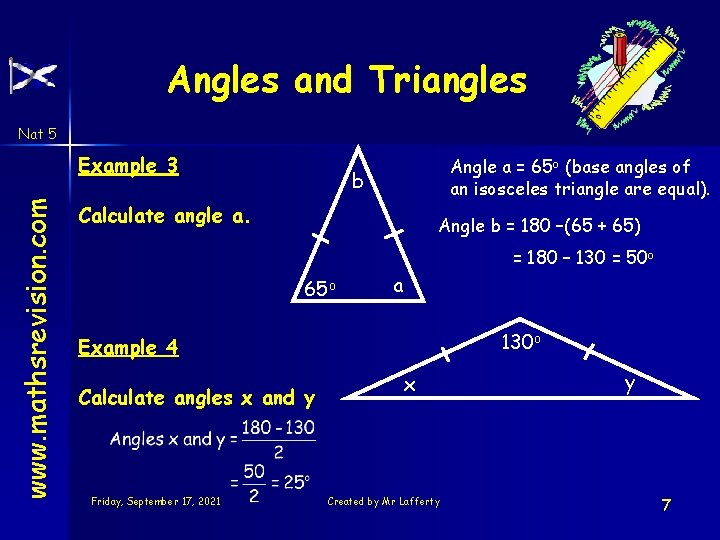
Angles and Triangles Nat 5 www. mathsrevision. com Example 3 Angle a = 65 o (base angles of an isosceles triangle are equal). b Calculate angle a. Angle b = 180 –(65 + 65) = 180 – 130 = 50 o 65 o a 130 o Example 4 Calculate angles x and y Friday, September 17, 2021 x Created by Mr Lafferty y 7

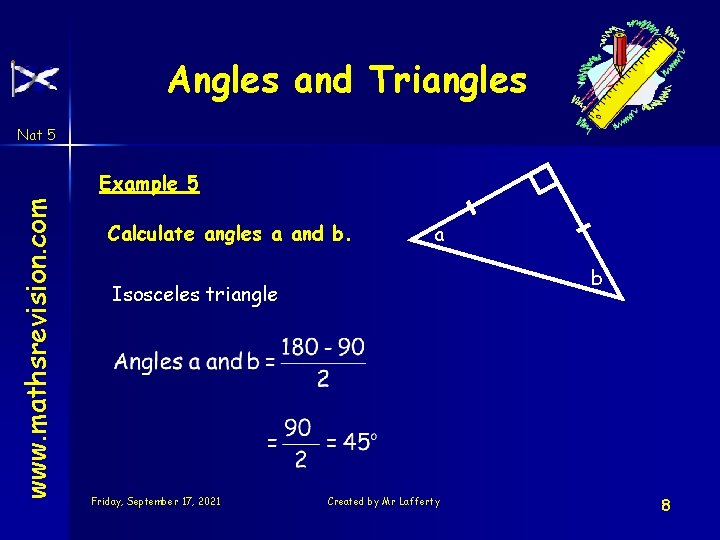
Angles and Triangles Nat 5 www. mathsrevision. com Example 5 Calculate angles a and b. a b Isosceles triangle Friday, September 17, 2021 Created by Mr Lafferty 8

Sum of Angles in a Triangle www. mathsrevision. com Nat 5 Copy out the following triangles and find the missing angles. x 87 o 50 o 32 o x o 38 o x o Remember all the angles add up to 180 17 -Sep-21 Created by Mr. Lafferty Math Dept o o

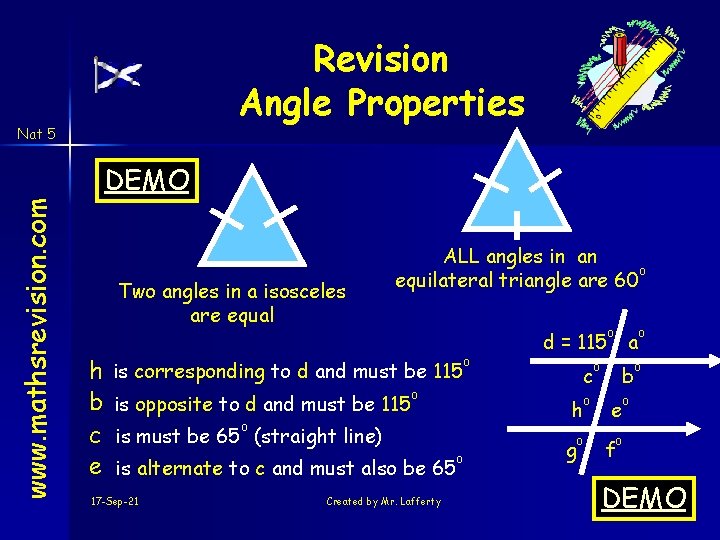
Revision Angle Properties www. mathsrevision. com Nat 5 DEMO Two angles in a isosceles are equal h b c e ALL angles in an o equilateral triangle are 60 is corresponding to d and must be 115 is opposite to d and must be 115 o o is alternate to c and must also be 65 17 -Sep-21 Created by Mr. Lafferty c h o is must be 65 (straight line) d = 115 o g o o o a o b e f o o DEMO

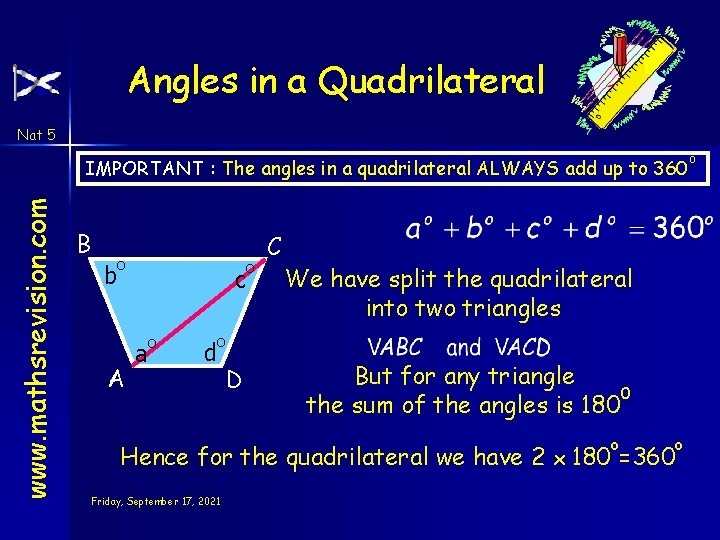
Angles in a Quadrilateral Nat 5 www. mathsrevision. com IMPORTANT : The angles in a quadrilateral ALWAYS add up to 360 B b o A c a o d o C We have split the quadrilateral into two triangles o D But for any triangle 0 the sum of the angles is 180 o Hence for the quadrilateral we have 2 x 180 =360 Friday, September 17, 2021 o o

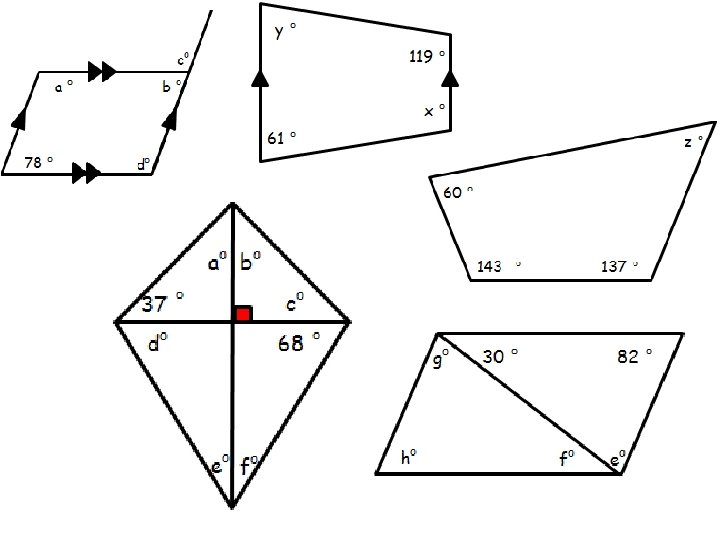
Angles in a Quadrilateral www. mathsrevision. com Nat 5 Question : Find the missing angle below. The four angles of a quadrilateral add to = 360 w z 34 x o o 100 y Friday, September 17, 2021 o o y Created by Mr. Lafferty 13

Circle Angle Properties www. mathsrevision. com Nat 5 Learning Intention Success Criteria 1. We are learning about isosceles triangles within circles. 1. Understand why isosceles triangles can be formed within circles. 2. Solve problems using properties. 17 -Sep-21 Created by Mr. Lafferty

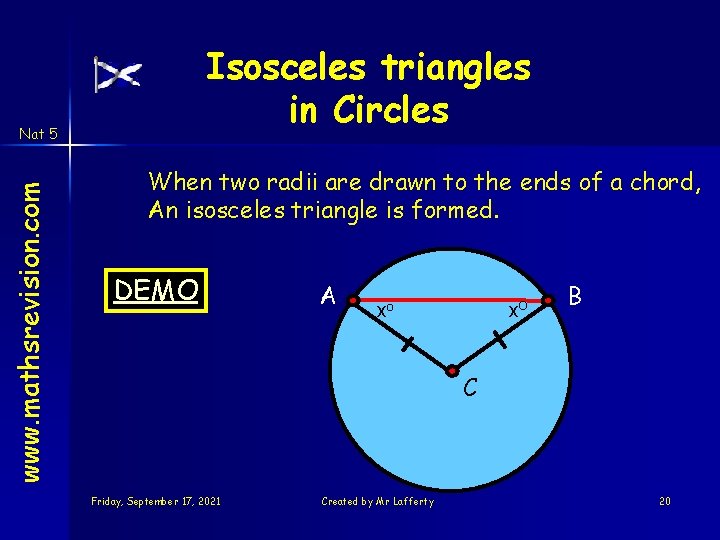
Isosceles triangles in Circles www. mathsrevision. com Nat 5 When two radii are drawn to the ends of a chord, An isosceles triangle is formed. DEMO A xo xo B C Friday, September 17, 2021 Created by Mr Lafferty 20

www. mathsrevision. com Nat 5 Isosceles triangles in Circles Special Properties of Isosceles Triangles Two equal lengths Two equal angles Angles in any triangle sum to 180 Friday, September 17, 2021 Created by Mr Lafferty o 21

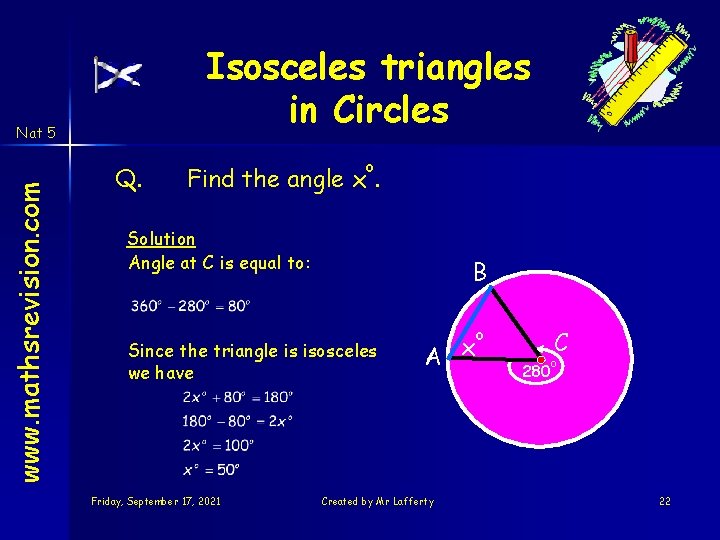
Isosceles triangles in Circles www. mathsrevision. com Nat 5 Q. o Find the angle x. Solution Angle at C is equal to: B Since the triangle is isosceles we have Friday, September 17, 2021 A x Created by Mr Lafferty o C 280 o 22

Circle Angle Properties www. mathsrevision. com Nat 5 Learning Intention Success Criteria 1. We are learning about angle in a semi-circle property. 1. Understand how a right angle is formed using semi -circle knowledge. 2. Solve problems using angle properties. 17 -Sep-21 Created by Mr. Lafferty

Angles in a Semi-Circle www. mathsrevision. com Nat 5 Key. Point for Angles in a Semi-circle P DEMO A A triangle APB inscribed within a semicircle with hypotenuse equal to the diameter will ALWAYS be right angled at P on the circumference. o Remember - Angles in any triangle sum to 180 Friday, September 17, 2021 Created by Mr Lafferty 26 B

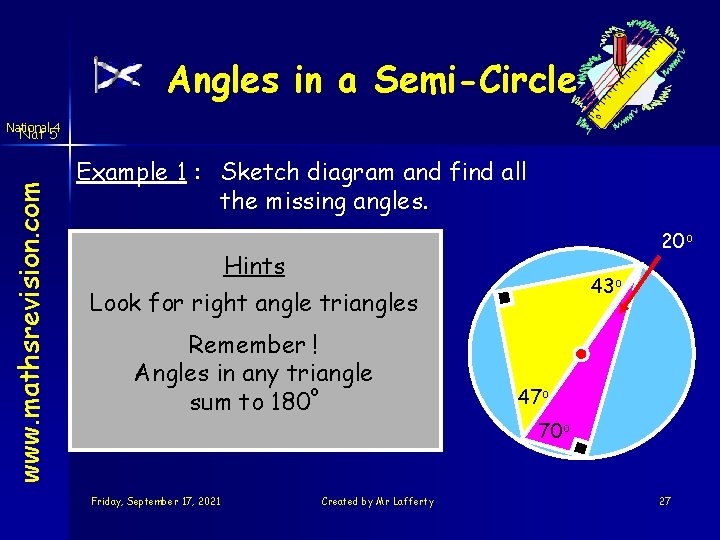
Angles in a Semi-Circle National 4 www. mathsrevision. com Nat 5 Example 1 : Sketch diagram and find all the missing angles. 20 o Hints 43 o Look for right angle triangles Remember ! Angles in any triangle o sum to 180 Friday, September 17, 2021 Created by Mr Lafferty 47 o 70 o 27

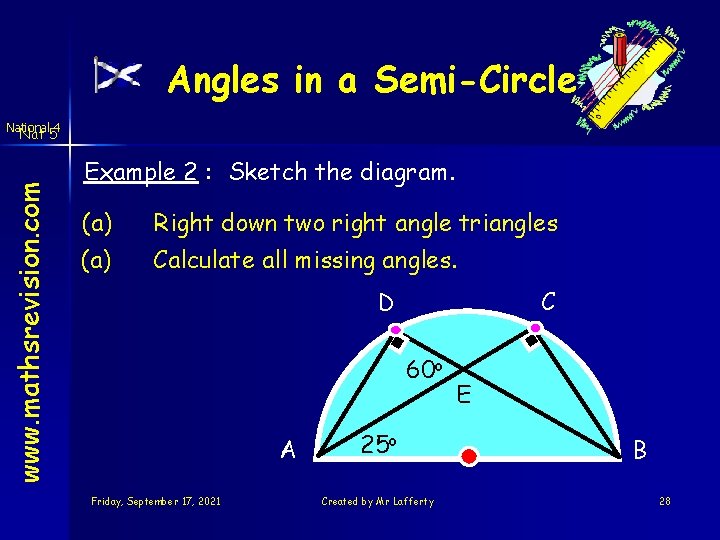
Angles in a Semi-Circle National 4 www. mathsrevision. com Nat 5 Example 2 : Sketch the diagram. (a) Right down two right angle triangles (a) Calculate all missing angles. C D 60 o A Friday, September 17, 2021 25 o Created by Mr Lafferty E B 28

Circle Angle Properties www. mathsrevision. com Nat 5 Learning Intention Success Criteria 1. We are learning the tangent property to a circle. 1. Understand the tangent property to a circle. 2. Solve problems using angle properties. 17 -Sep-21 Created by Mr. Lafferty

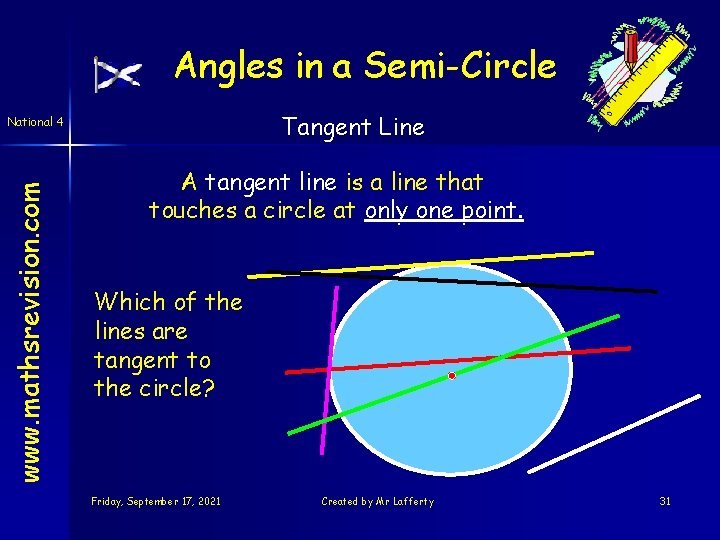
Angles in a Semi-Circle Tangent Line www. mathsrevision. com National 4 A tangent line is a line that touches a circle at only one point. Which of the lines are tangent to the circle? Friday, September 17, 2021 Created by Mr Lafferty 31

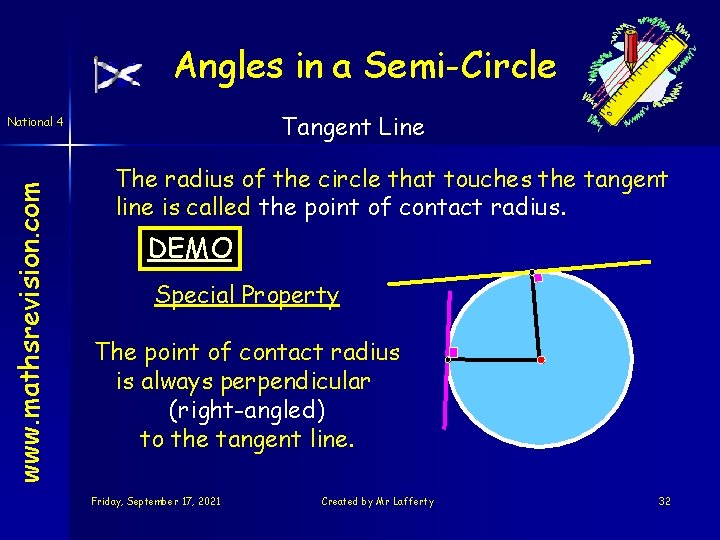
Angles in a Semi-Circle Tangent Line www. mathsrevision. com National 4 The radius of the circle that touches the tangent line is called the point of contact radius. DEMO Special Property The point of contact radius is always perpendicular (right-angled) to the tangent line. Friday, September 17, 2021 Created by Mr Lafferty 32

Polygons Interior and Exterior Angles www. mathsrevision. com Nat 5 Learning Intention Success Criteria 1. We are learning about interior and exterior angles for polygons. 1. Understand the terms interior and exterior angles. 2. Be able to calculate interior and exterior angles for a polygon. 17 -Sep-21 Created by Mr. Lafferty

Polygons Interior and Exterior Angles Nat 5 www. mathsrevision. com A polygon is a “many-sided closed straight-lined figure” This 5 -sided (polygon) is called a PENTAGON Irregular Pentagon 17 -Sep-21 Created by Mr. Lafferty

Polygons Interior and Exterior Angles Nat 5 www. mathsrevision. com A polygon is a “many-sided closed straight-lined figure” If all the sides and angles are the same it is called REGULAR POLYGON. We will only be dealing with regular polygons in this section. Pentagon 17 -Sep-21 Hexagon Created by Mr. Lafferty Octagon

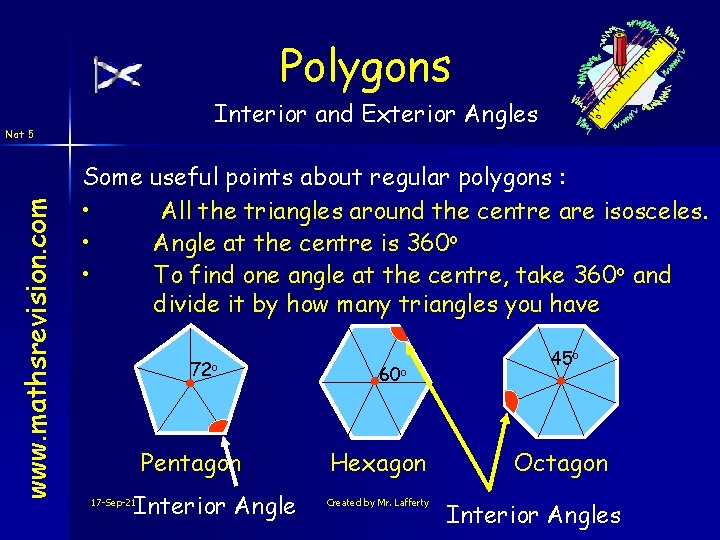
Polygons Interior and Exterior Angles www. mathsrevision. com Nat 5 Some useful points about regular polygons : • All the triangles around the centre are isosceles. • Angle at the centre is 360 o • To find one angle at the centre, take 360 o and divide it by how many triangles you have 72 o Pentagon Interior Angle 17 -Sep-21 60 o Hexagon Created by Mr. Lafferty 45 o Octagon Interior Angles

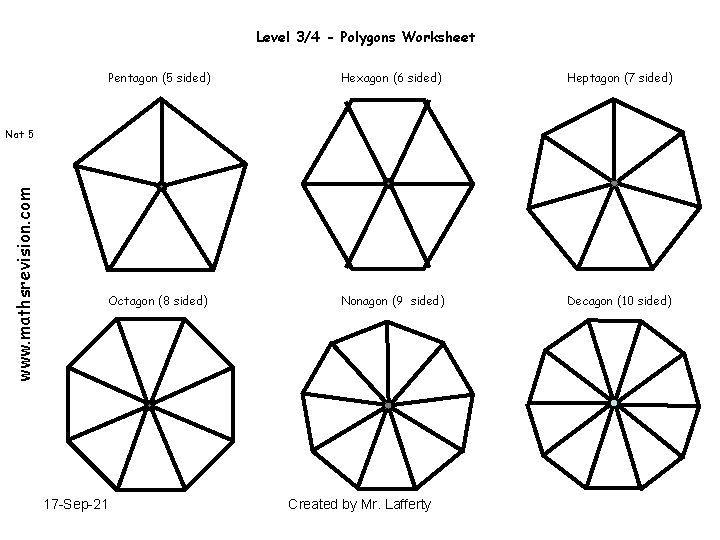
Level 3/4 - Polygons Worksheet Pentagon (5 sided) Hexagon (6 sided) Heptagon (7 sided) Octagon (8 sided) Nonagon (9 sided) Decagon (10 sided) www. mathsrevision. com Nat 5 17 -Sep-21 Created by Mr. Lafferty

Polygons Interior and Exterior Angles Nat 5 www. mathsrevision. com What you should have found : Interior angle = 180 – (360÷n) n = Number of sides eg. A hexagonal has interior angle is: Interior angle = 180 – (360÷ 6) = 120 o 17 -Sep-21 Created by Mr. Lafferty

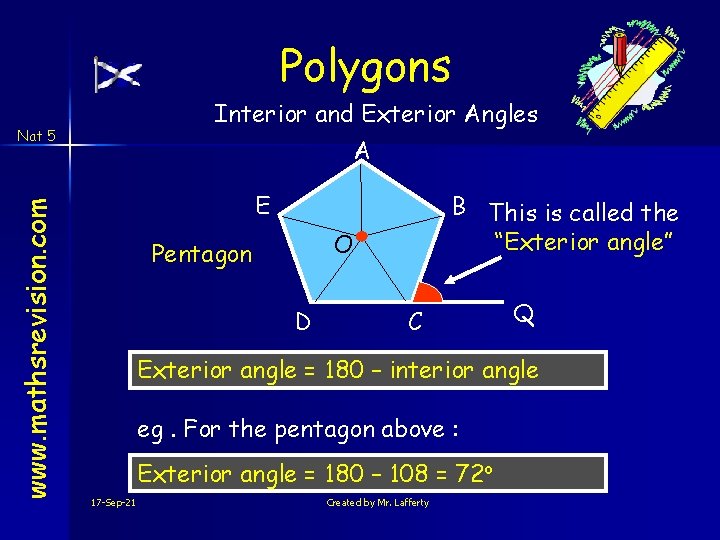
Polygons Interior and Exterior Angles www. mathsrevision. com Nat 5 A E B This is called the “Exterior angle” O Pentagon D C Q Exterior angle = 180 – interior angle eg. For the pentagon above : Exterior angle = 180 – 108 = 72 o 17 -Sep-21 Created by Mr. Lafferty

Level 3/4 - Polygons Worksheet Pentagon (5 sided) Hexagon (6 sided) Heptagon (7 sided) Octagon (8 sided) Nonagon (9 sided) Decagon (10 sided) www. mathsrevision. com Nat 5 17 -Sep-21 Created by Mr. Lafferty

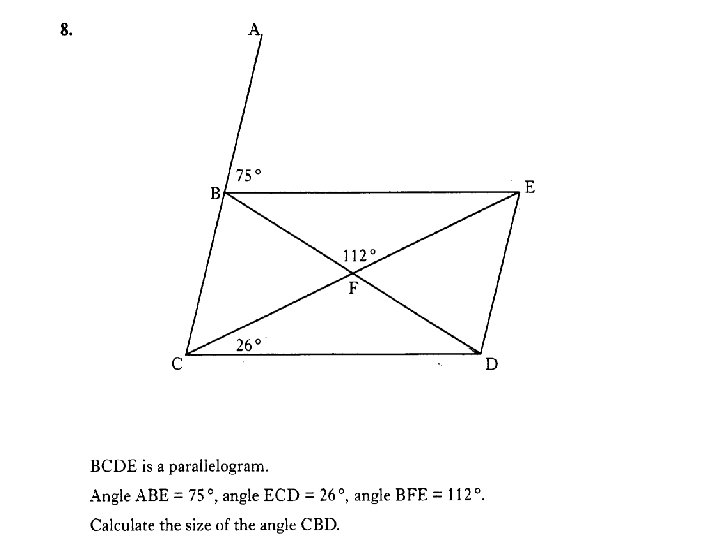
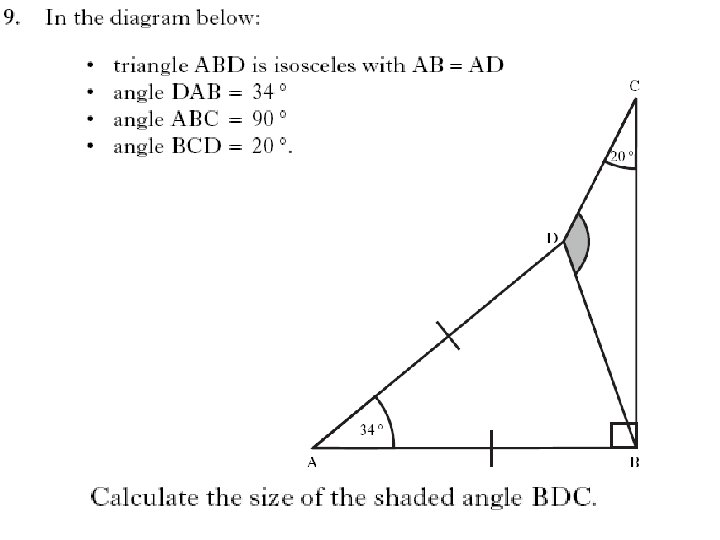
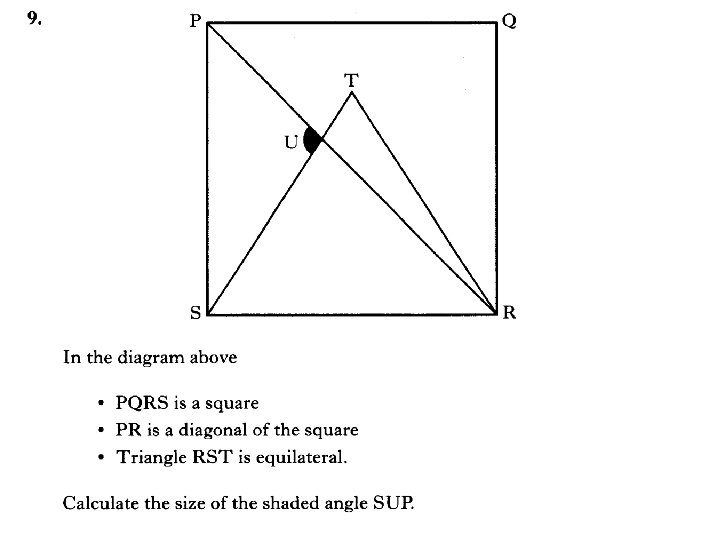
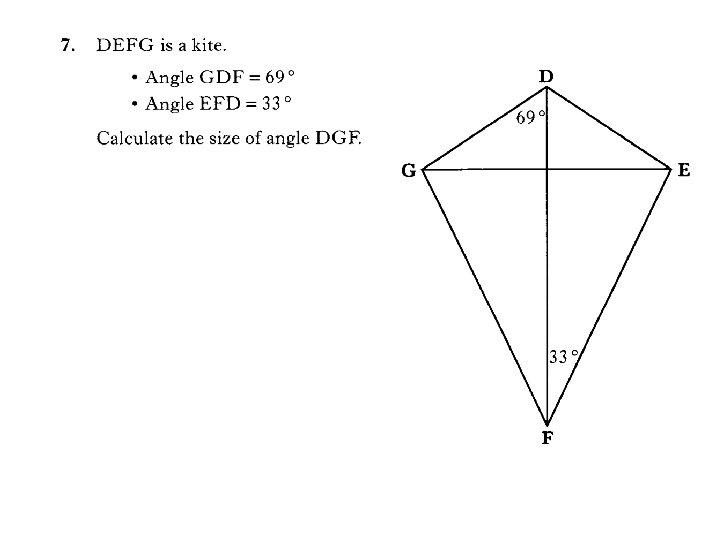
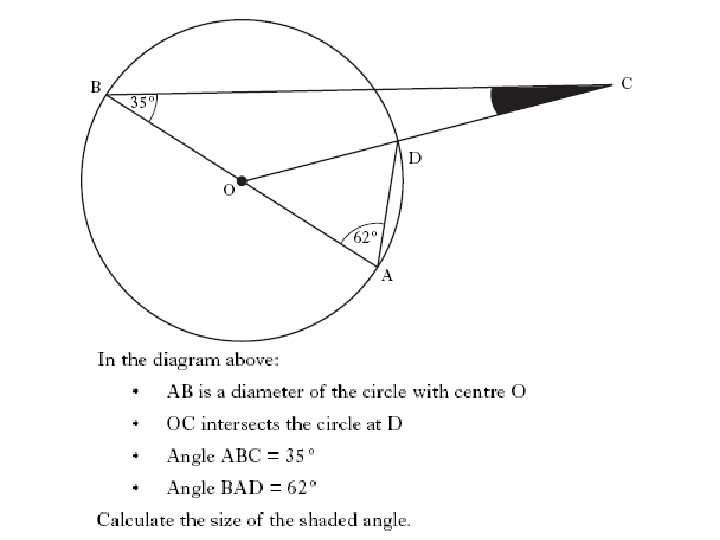
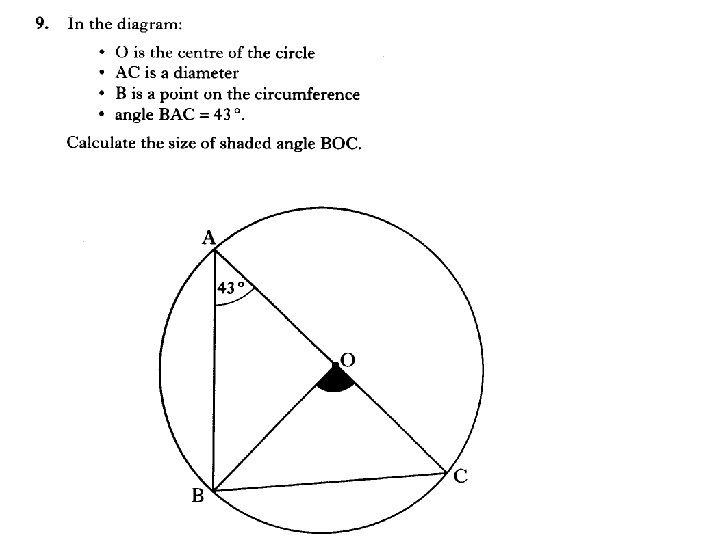
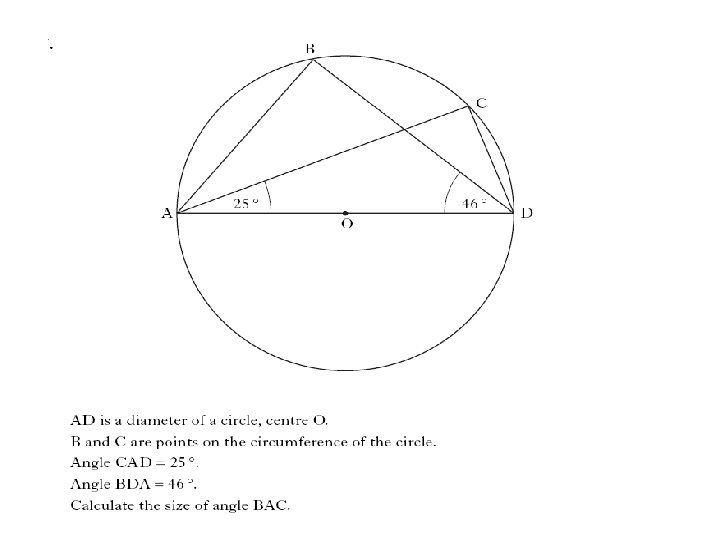
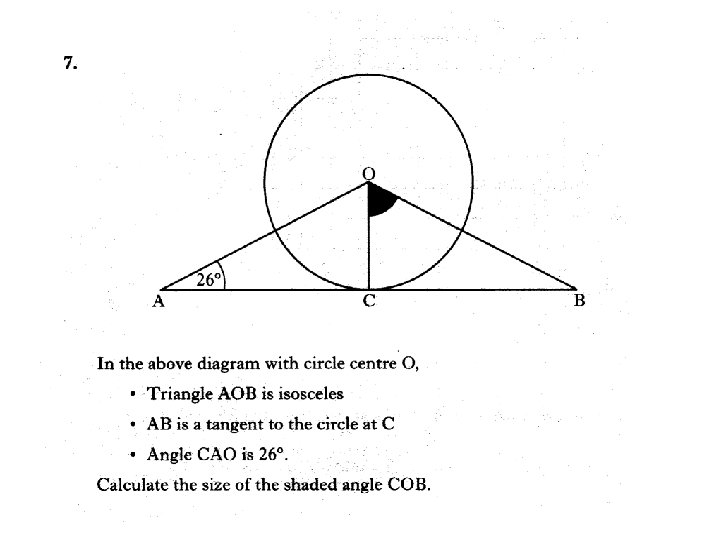
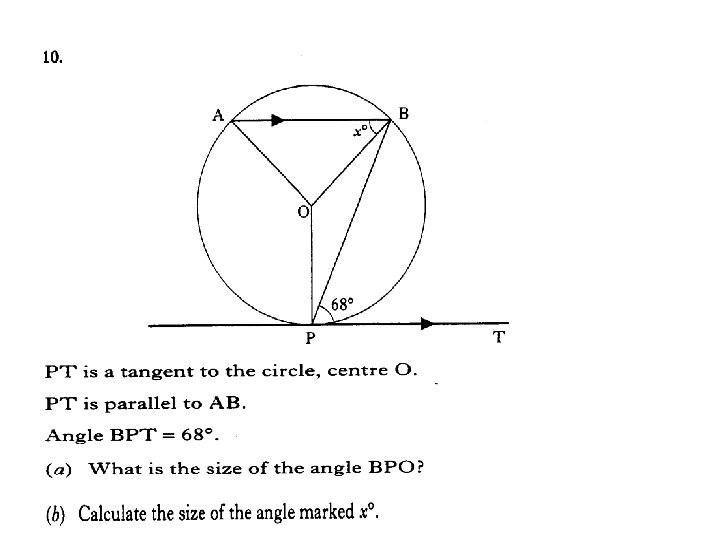
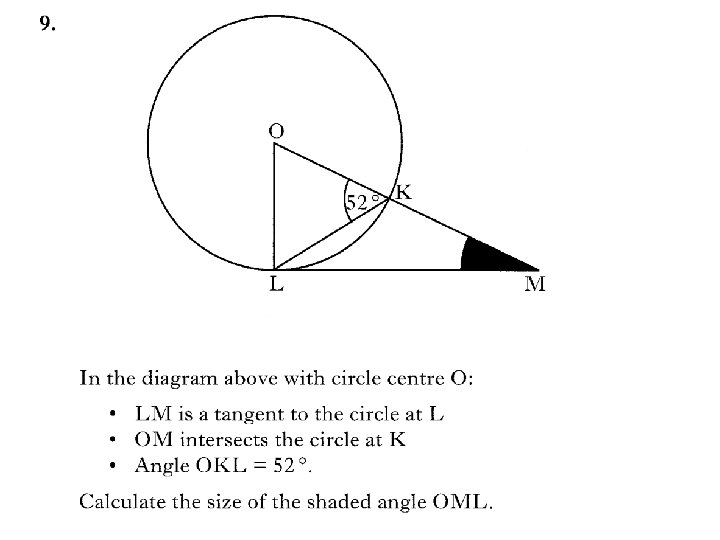
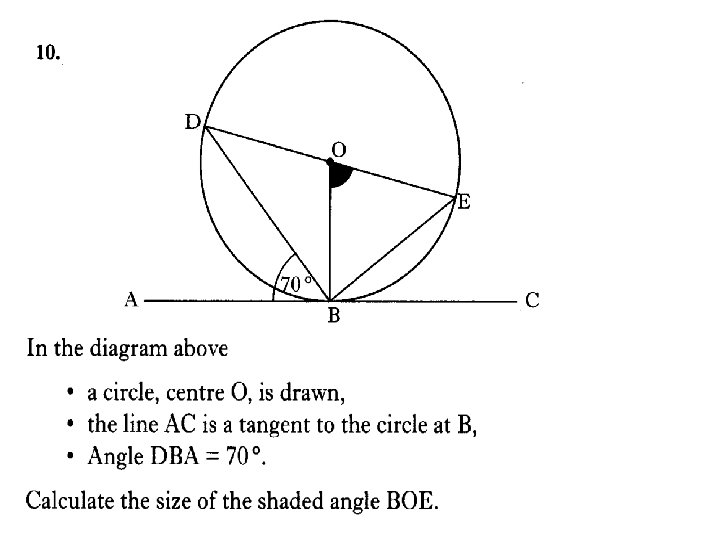
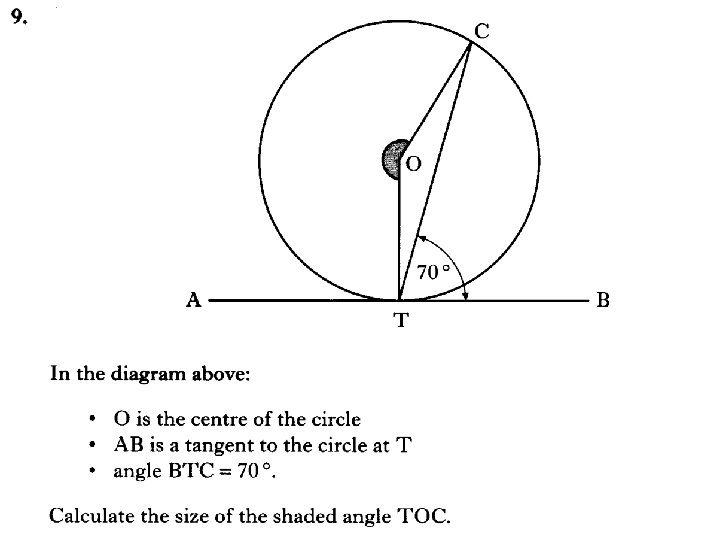
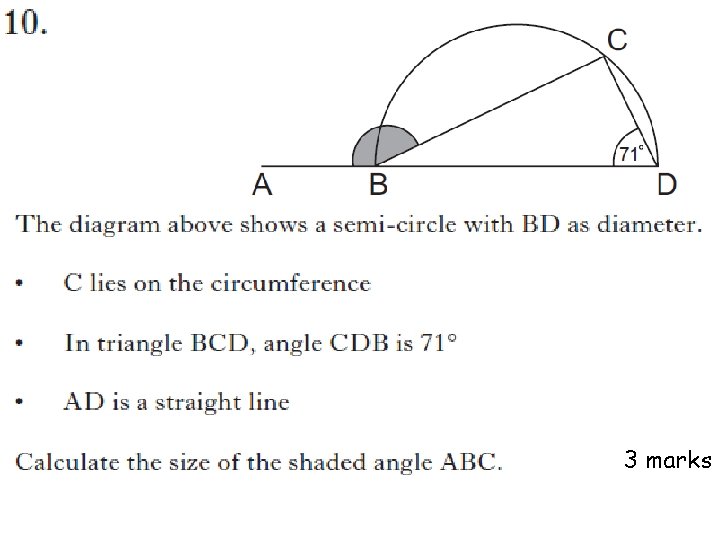
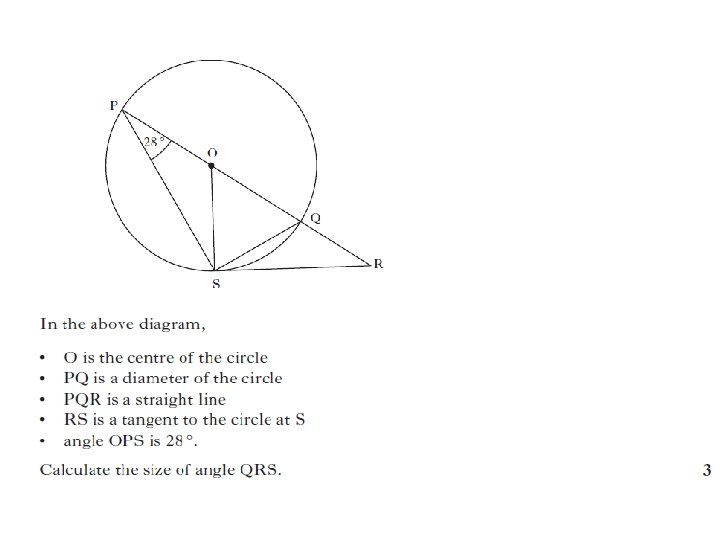
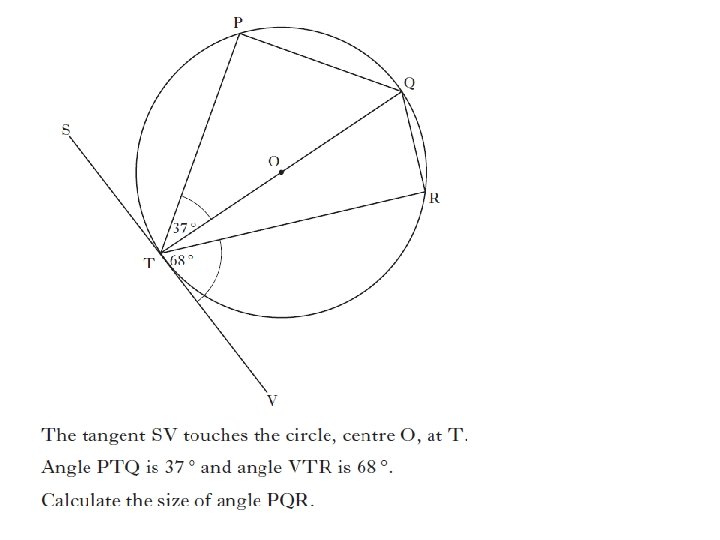
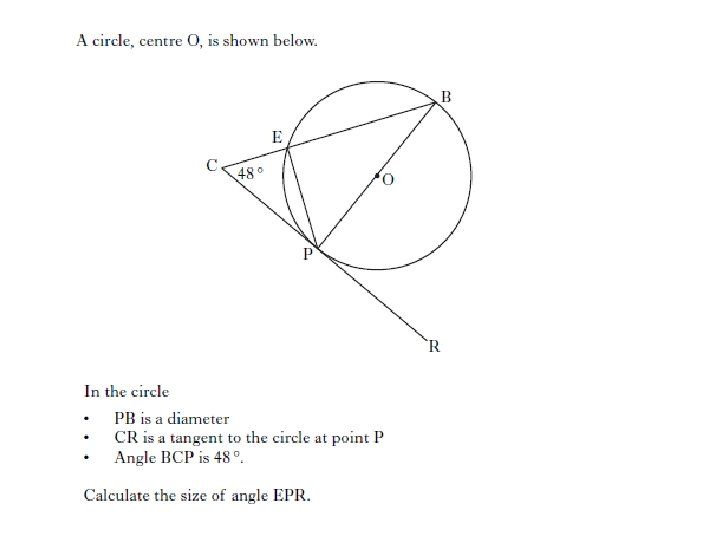
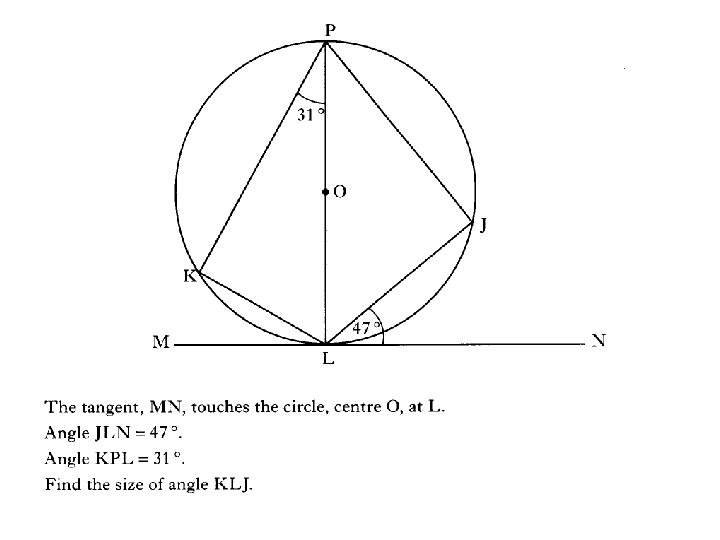
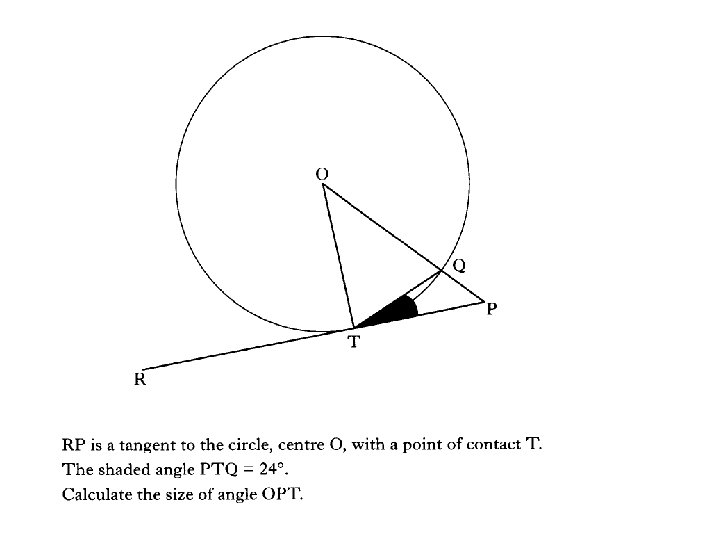
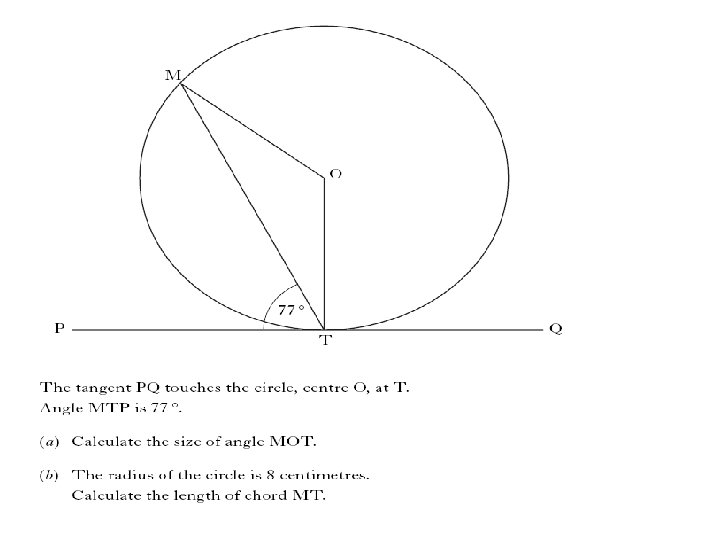
3 marks