ANGLE PAIR RELATIONSHIP S Angles An angle is

ANGLE PAIR RELATIONSHIP S

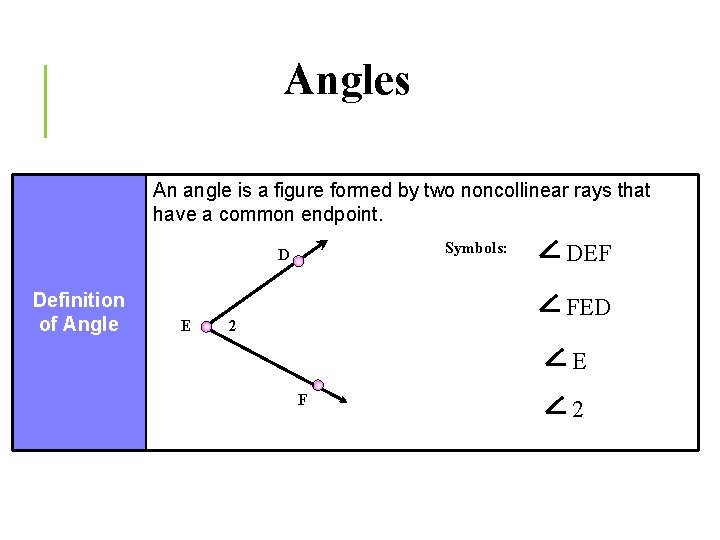
Angles An angle is a figure formed by two noncollinear rays that have a common endpoint. Symbols: D Definition of Angle E DEF FED 2 E F 2

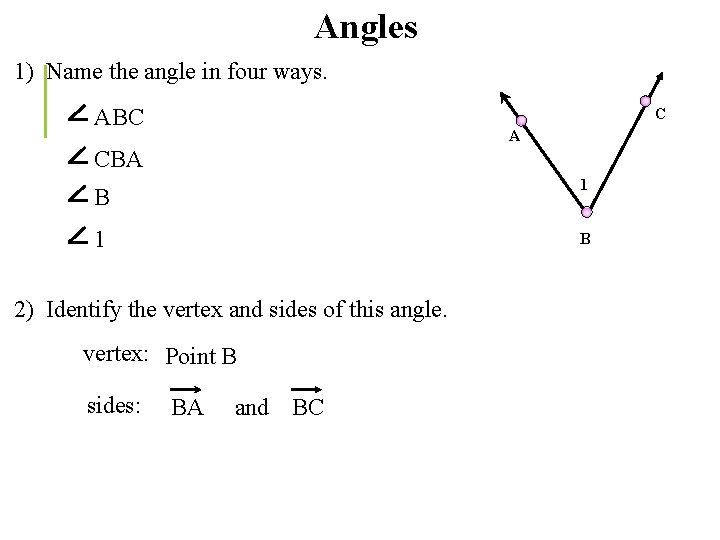
Angles 1) Name the angle in four ways. ABC C A CBA 1 B 2) Identify the vertex and sides of this angle. vertex: Point B sides: BA and BC

Angles 1) Name all angles having W as their vertex. X 1 2 W 1 2 XWZ Y 2) What are other names for XWY or 1 ? YWX 3) Is there an angle that can be named No! Z W?

Adjacent Angles When you “split” an angle, you create two angles. The two angles are called _______ adjacent angles adjacent = next to, joining. A B D 2 1 1 and 2 are examples of adjacent angles. They share a common ray. Name the ray that 1 and 2 have in common. C ____

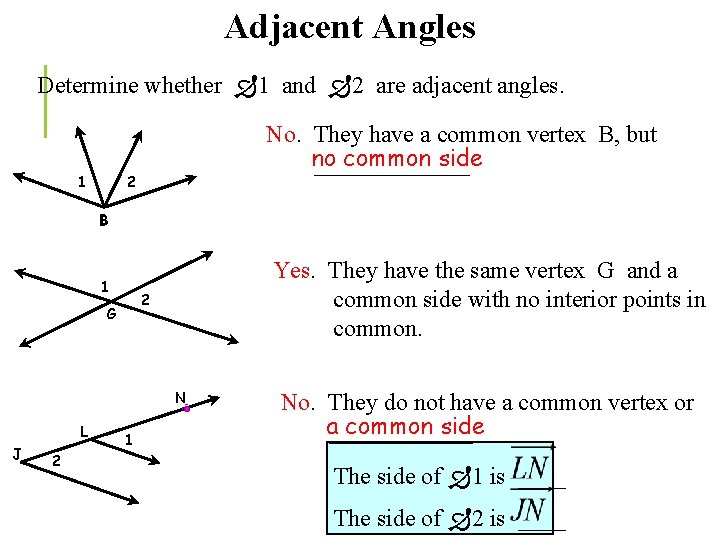
Adjacent Angles Determine whether 1 and 2 are adjacent angles. No. They have a common vertex B, but no common side _______ 2 1 B 1 Yes. They have the same vertex G and a common side with no interior points in common. 2 G N L J 2 1 No. They do not have a common vertex or a______ common side The side of 1 is ____ The side of 2 is ____

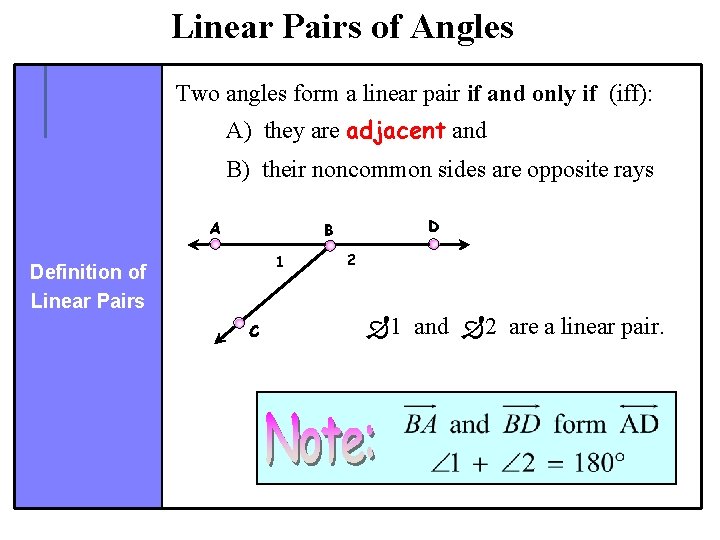
Linear Pairs of Angles Two angles form a linear pair if and only if (iff): A) they are adjacent and B) their noncommon sides are opposite rays A D B 1 Definition of Linear Pairs C 2 1 and 2 are a linear pair.

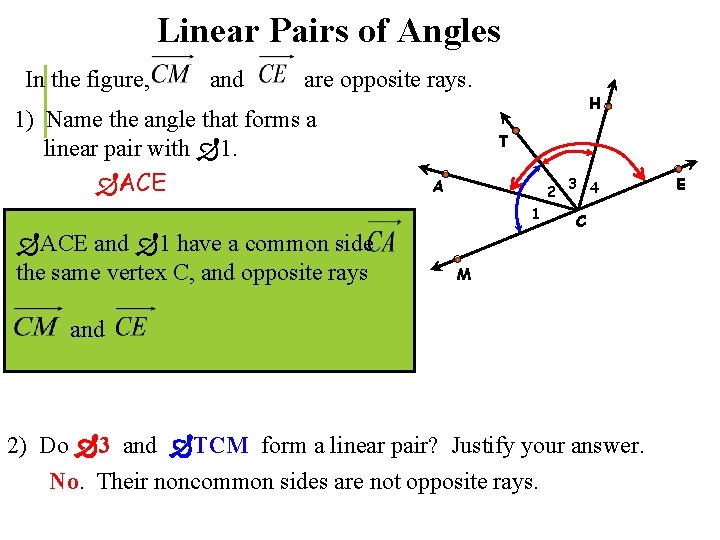
Linear Pairs of Angles In the figure, and are opposite rays. 1) Name the angle that forms a linear pair with 1. ACE H T A 2 1 ACE and 1 have a common side the same vertex C, and opposite rays 3 4 C M and 2) Do 3 and TCM form a linear pair? Justify your answer. No. Their noncommon sides are not opposite rays. E

Complementary and Supplementary Angles Two angles are complementary if and only if (iff) The sum of their degree measure is 90. E D A Definition of Complementary Angles B 30° 60° F C m ABC + m DEF = 30 + 60 = 90 Notes: “m” stands for “measure”

Complementary and Supplementary Angles If two angles are complementary, each angle is a complement of the other. ABC is the complement of DEF and DEF is the complement of ABC. E A B D 30° C 60° F Complementary angles DO NOT need to have a common side or even the same vertex.

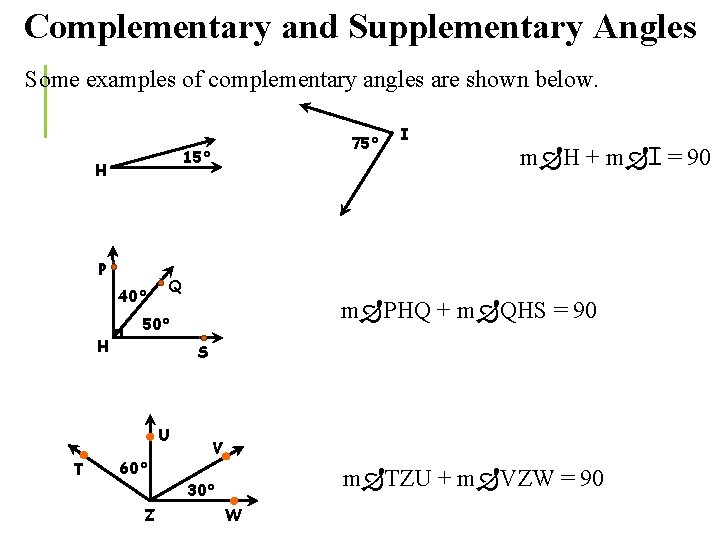
Complementary and Supplementary Angles Some examples of complementary angles are shown below. 75° 15° H P 40° m H + m I = 90 Q m PHQ + m QHS = 90 50° H S U T I 60° Z V m TZU + m VZW = 90 30° W

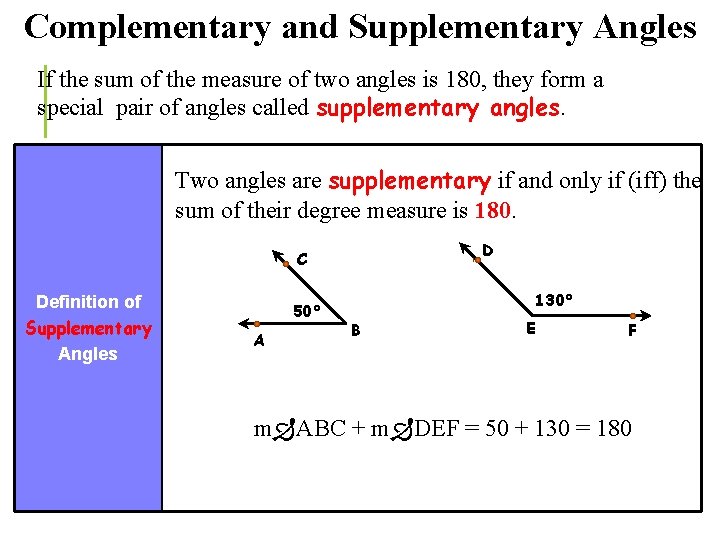
Complementary and Supplementary Angles If the sum of the measure of two angles is 180, they form a special pair of angles called supplementary angles. Two angles are supplementary if and only if (iff) the sum of their degree measure is 180. D C Definition of Supplementary Angles 50° A 130° B E F m ABC + m DEF = 50 + 130 = 180

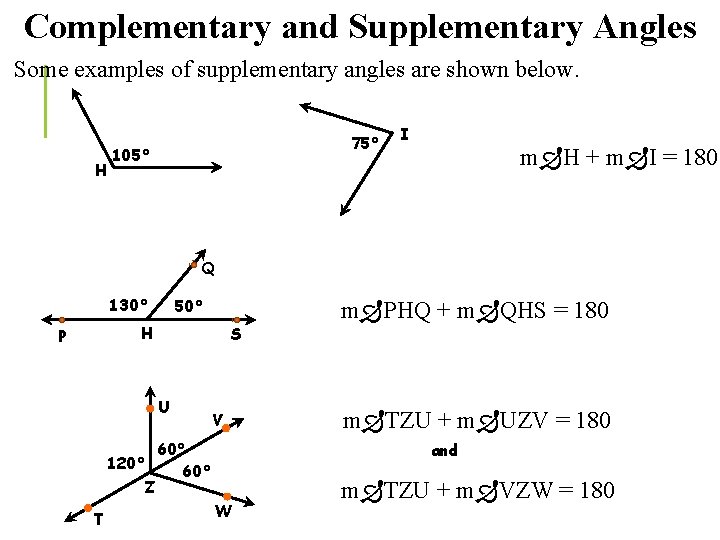
Complementary and Supplementary Angles Some examples of supplementary angles are shown below. H 75° 105° I m H + m I = 180 Q 130° 50° H P S U V 60° 120° 60° Z T m PHQ + m QHS = 180 m TZU + m UZV = 180 and W m TZU + m VZW = 180

Congruent Angles measure Recall that congruent segments have the same ____. Congruent angles ________ also have the same measure.

Congruent Angles Two angles are congruent iff, they have the same degree measure _______. Definition of Congruent Angles B V iff 50° B V m B = m V

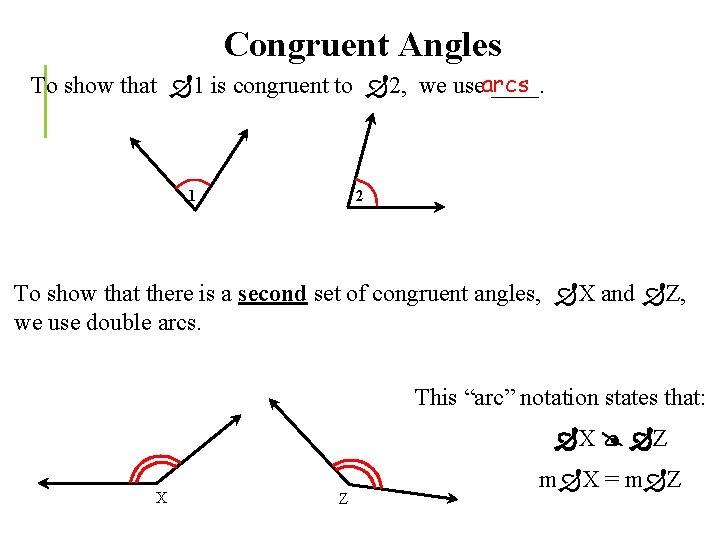
Congruent Angles To show that 1 is congruent to 2, we usearcs ____. 1 2 To show that there is a second set of congruent angles, X and Z, we use double arcs. This “arc” notation states that: X Z X Z m X = m Z

Congruent Angles G D 1 1) If m 1 = 2 x + 3 and the m 3 = 3 x + 2, then find the m 3 A x = 17; 3 = 37° 4 3 B 2 C E H 2) If m ABD = 4 x + 5 and the m DBC = 2 x + 1, then find the m EBC x = 29; EBC = 121° 3) If m 1 = 4 x - 13 and the m 3 = 2 x + 19, then find the m 4 x = 16; 4 = 39° 4) If m EBG = 7 x + 11 and the m EBH = 2 x + 7, then find the m 1 x = 18; 1 = 43°

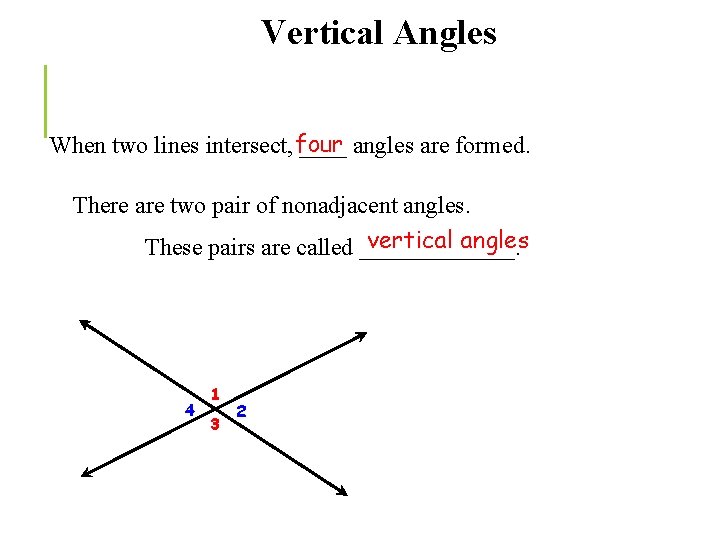
Vertical Angles When two lines intersect, four ____ angles are formed. There are two pair of nonadjacent angles. vertical angles These pairs are called _______. 4 1 3 2

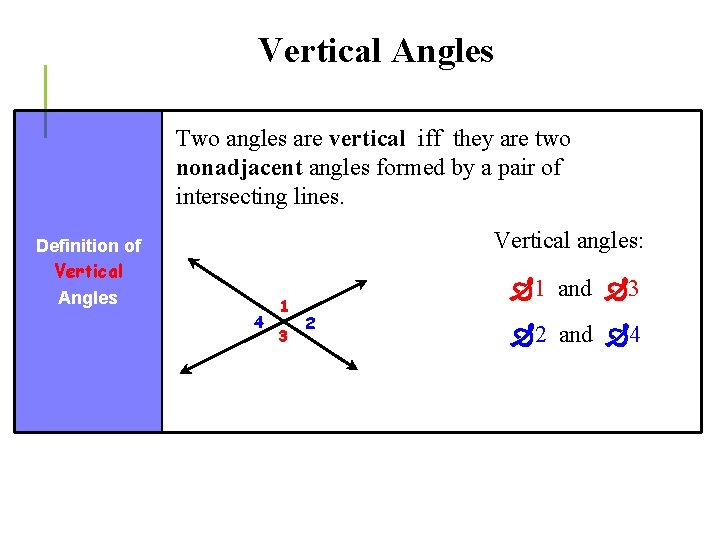
Vertical Angles Two angles are vertical iff they are two nonadjacent angles formed by a pair of intersecting lines. Vertical angles: Definition of Vertical Angles 4 1 3 1 and 3 2 2 and 4

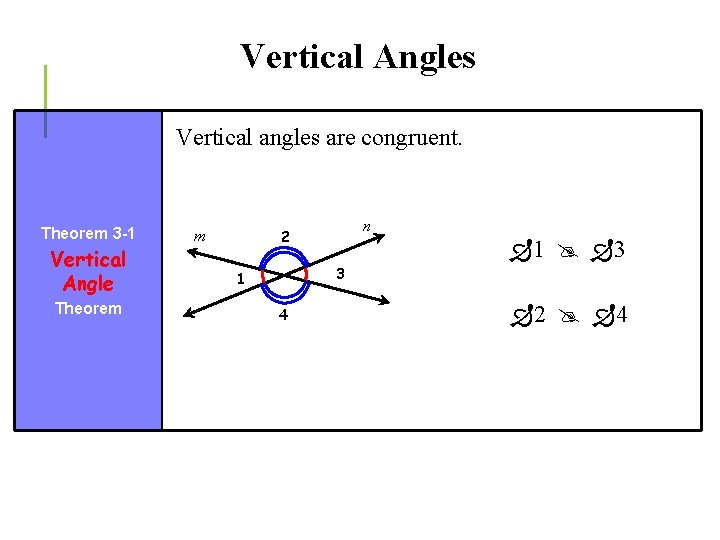
Vertical Angles Vertical angles are congruent. Theorem 3 -1 Vertical Angle Theorem m n 2 1 3 3 1 4 2 4

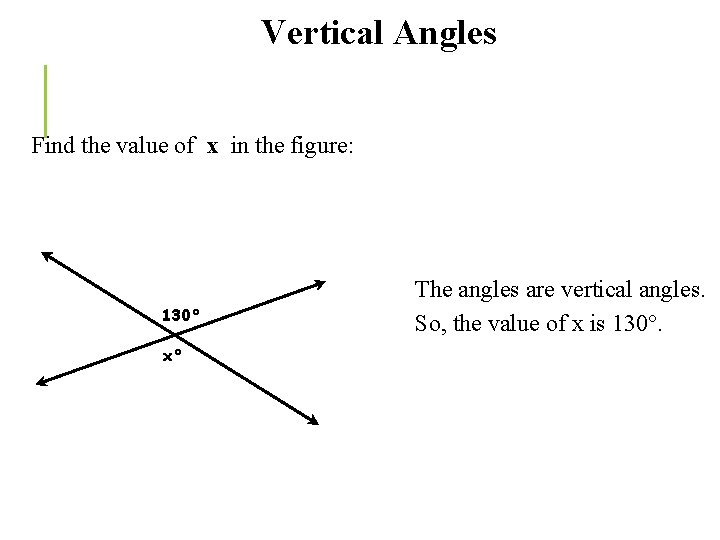
Vertical Angles Find the value of x in the figure: 130° x° The angles are vertical angles. So, the value of x is 130°.

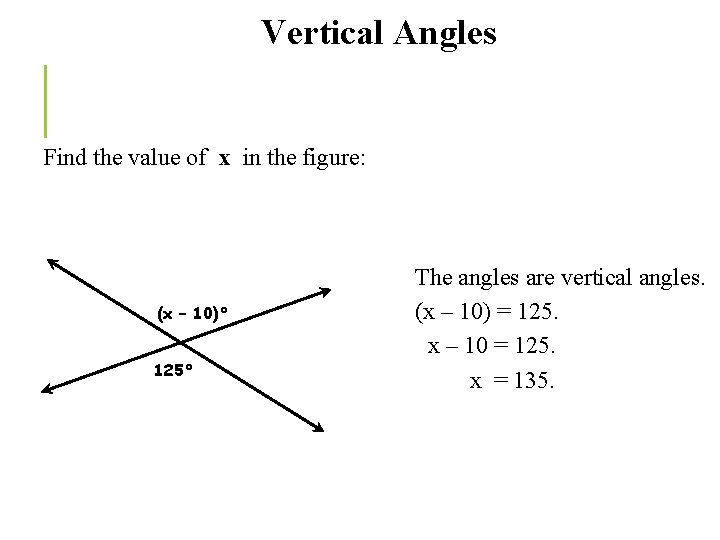
Vertical Angles Find the value of x in the figure: (x – 10)° 125° The angles are vertical angles. (x – 10) = 125. x – 10 = 125. x = 135.

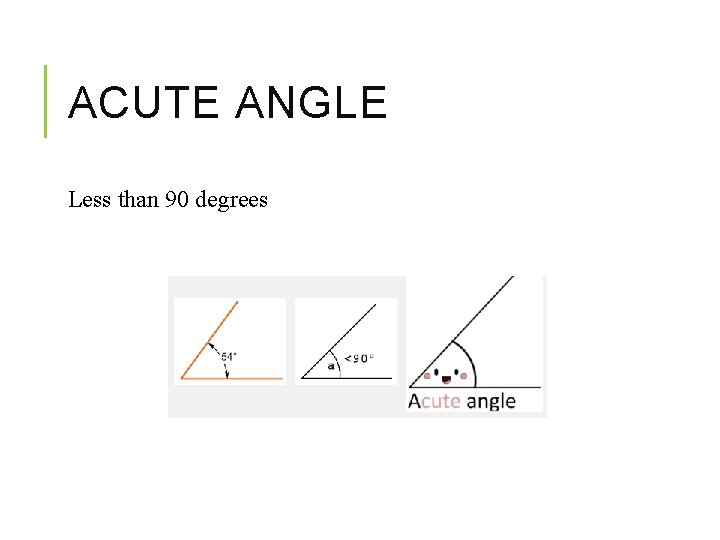
ACUTE ANGLE Less than 90 degrees

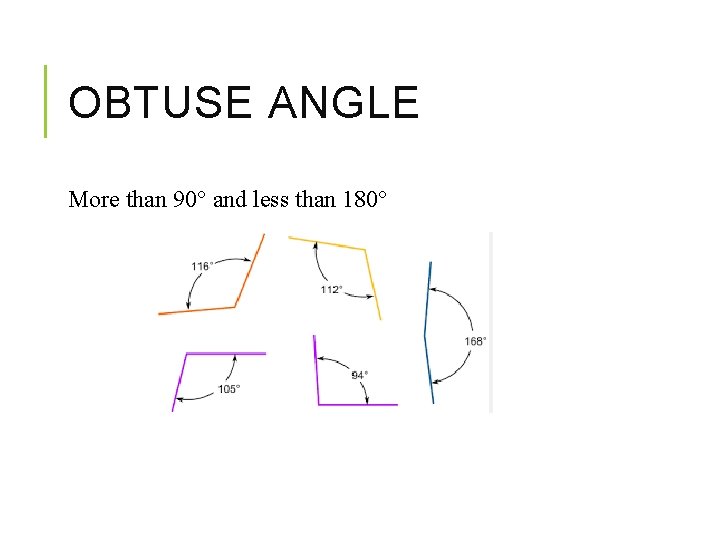
OBTUSE ANGLE More than 90° and less than 180°

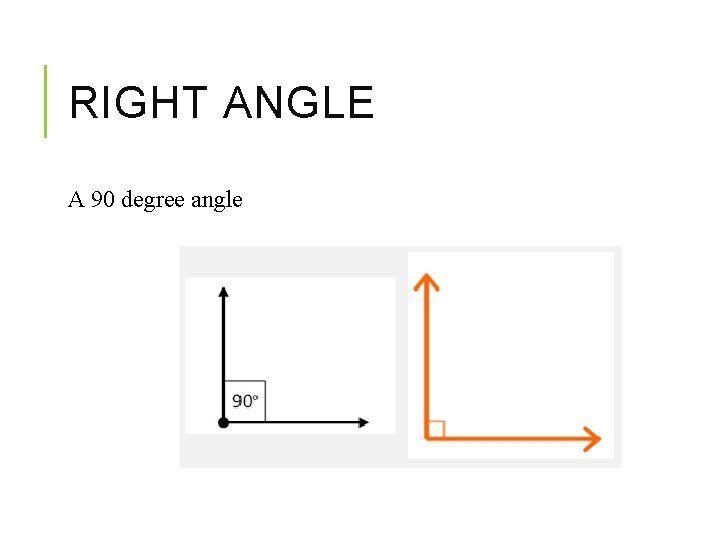
RIGHT ANGLE A 90 degree angle