Angle Modulation Phase Modulation or Frequency Modulation Basic

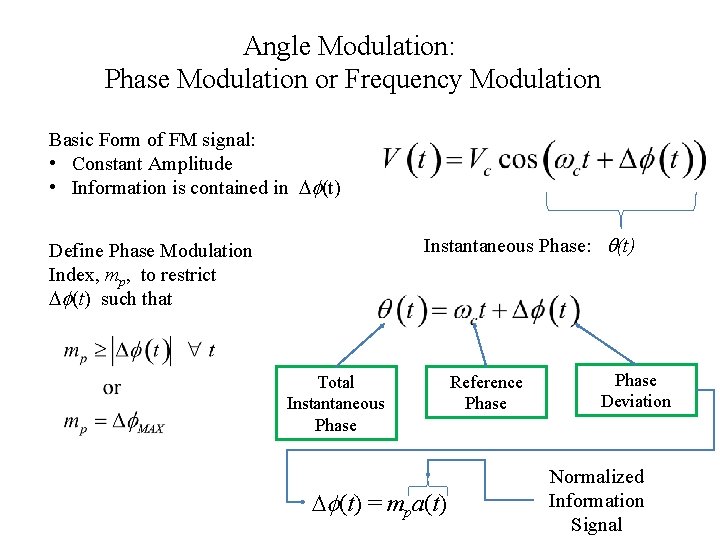
Angle Modulation: Phase Modulation or Frequency Modulation Basic Form of FM signal: • Constant Amplitude • Information is contained in Df(t) Instantaneous Phase: q(t) Define Phase Modulation Index, mp, to restrict Df(t) such that Total Instantaneous Phase Df(t) = mpa(t) Reference Phase Deviation Normalized Information Signal

Visualizing the FM Phasor. . . …down at the “Complex Plane” wc wc FM Phasor Df(t) = mpa(t) wc Reference Phasor Constant Amplitude Reference Phase Df(t) mp = |Df. MAX|

Instantaneous Frequency Deviation Time Waveform: Phasor Notation: “Carrier Frequency” Instantaneous “Frequency Deviation” Can be very large and still have |a(t)| < 1 High rates of change implies Wide Bandwidth

Voltage Controlled Oscillator (VCO) “Free running” frequency fc (hz or R/s ) k 0 (hz/v or R/s/v) VCO Deviation Sensitivity fout fc k 0 Frequency deviation: of. DVCO f(t) Output Frequency vin “Reference” phase Phase Deviation: Df(t)

Simple Case For Analysis

FM Spectrum Now all we have to do is take the Fourier Transform of this thing. . . Spectral Analysis: High Math. Spectrum is characterized by spectral components spaced at + nwm from wc, with amplitudes determined by Bessel Functions Jn(mp). J 1 J 0 wm J 2 J 3 wc J 4

J 0(m) J 1(m) J 2(m) J 3(m) J 4(m) J 5(m) J 6(m) J 7(m) J 8(m) J 9(m) J 10(m)

Bessel Function Tabulation The Bessel Function values determine the relative voltage amplitudes of their respective sidebands. The squares of the Bessel Function values determine the relative power amplitudes of their respective sidebands. For any value of m: If our Bandwidth includes N sidebands, then :