Angle Facts Foundation GCSE Questions AQA These questions

Angle Facts – Foundation – GCSE Questions – AQA These questions are the same format as previous GCSE exams. COPY means they use the exact same numbers as the original GCSE question. Otherwise, they are clone questions using different numbers. The worksheets are provided in 2 sizes.

Printing To print handouts from slides Select the slide from the left. Then click: File > Print > ‘Print Current Slide’ To print multiple slides Click on a section title to highlight all those slides, or press ‘Ctrl’ at the same time as selecting slides to highlight more than one. Then click: File > Print > ‘Print Selection’ To print double-sided handouts Highlight both slides before using ‘Print Selection’. Choose ‘Print on Both Sides’ and ‘Flip on Short Edge’.

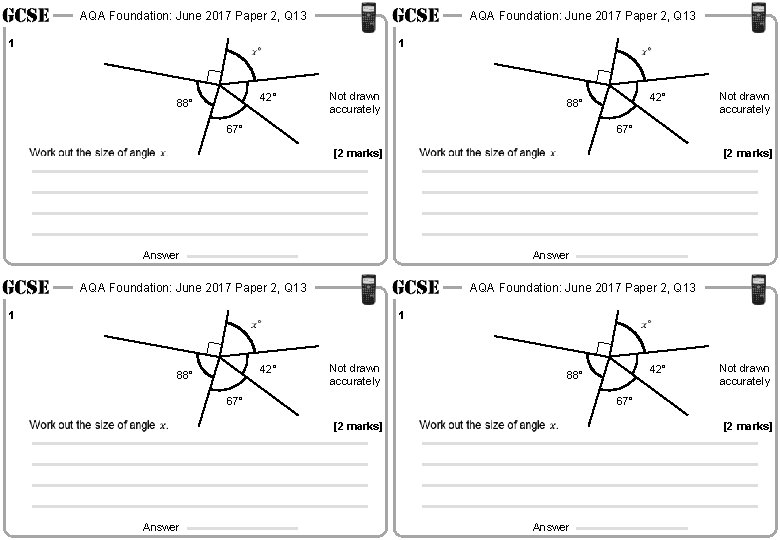
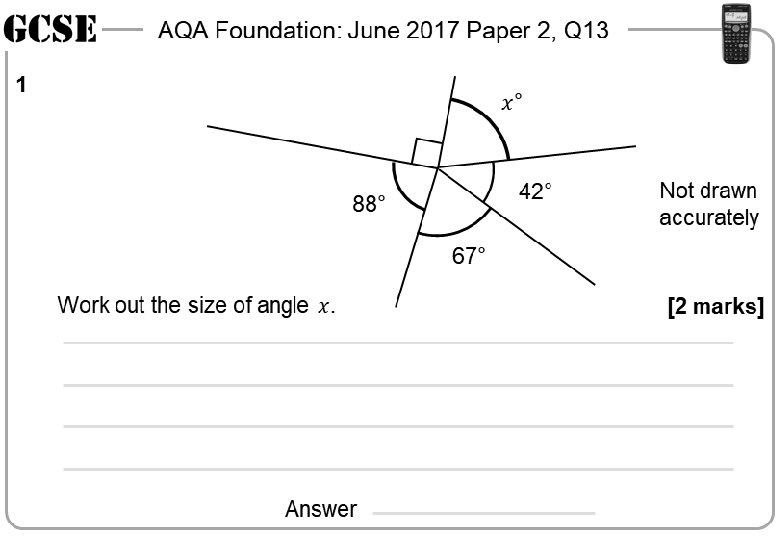
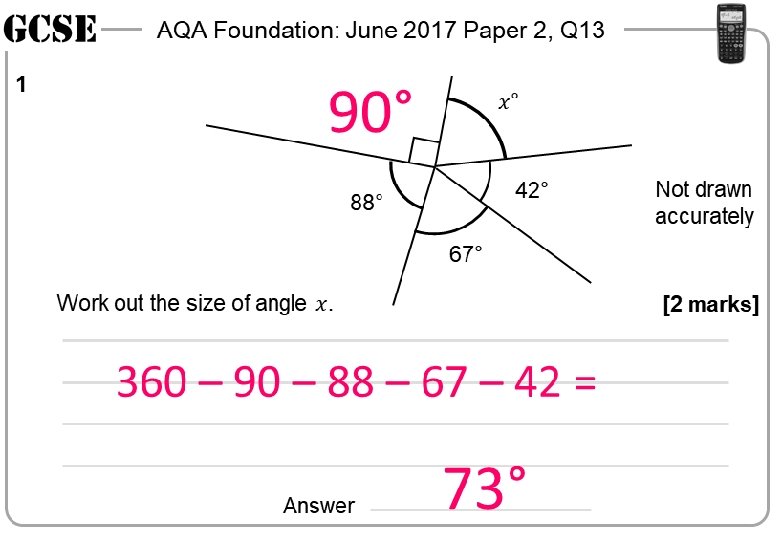
AQA Foundation: June 2017 Paper 2, Q 13 1 1 42° 88° Not drawn accurately 42° 88° 67° Not drawn accurately 67° [2 marks] Answer AQA Foundation: June 2017 Paper 2, Q 13 1 1 42° 88° Not drawn accurately 67° [2 marks] Answer 42° 88° [2 marks] Answer

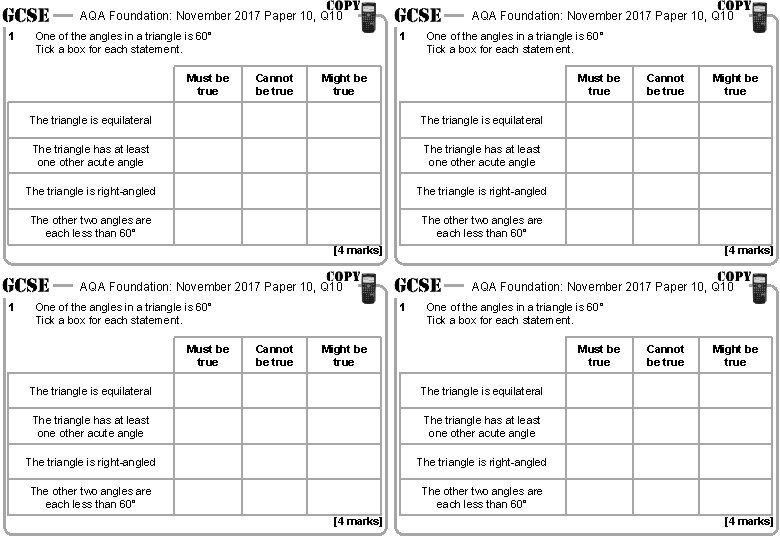
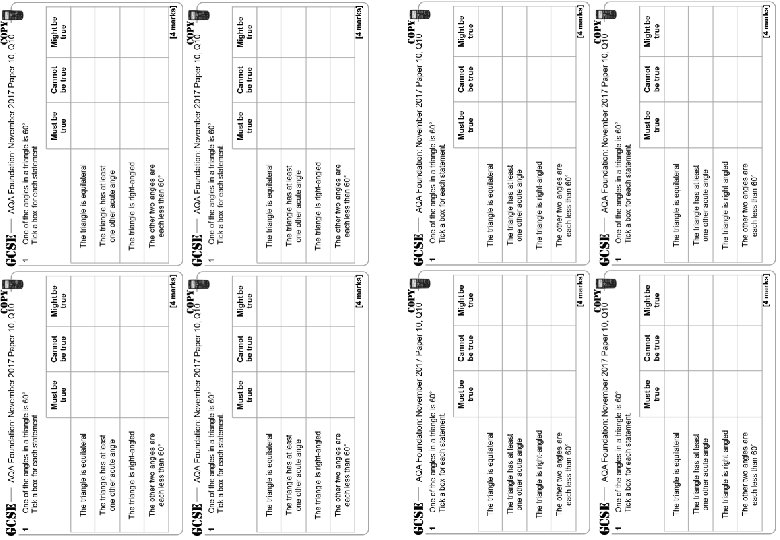
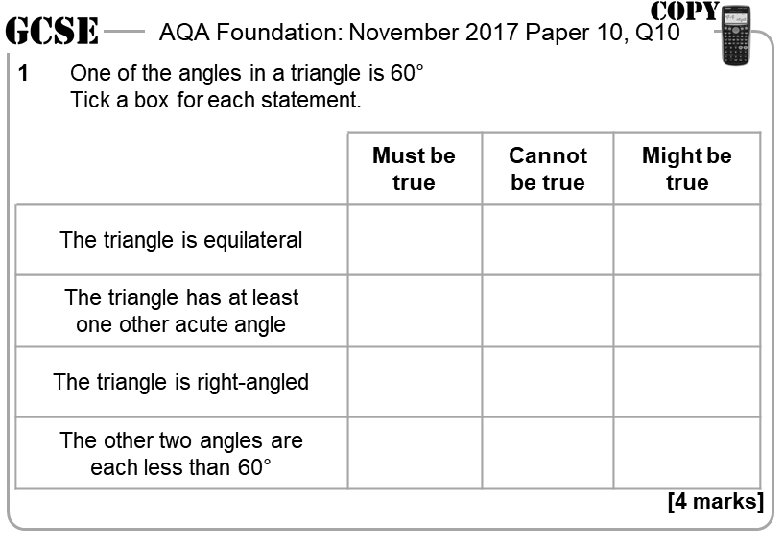
AQA Foundation: November 2017 Paper 10, Q 10 1 1 One of the angles in a triangle is 60° Tick a box for each statement. Must be true AQA Foundation: November 2017 Paper 10, Q 10 Cannot be true One of the angles in a triangle is 60° Tick a box for each statement. Might be true Must be true The triangle is equilateral Cannot be true The triangle is equilateral The triangle is right-angled The triangle has at least one other acute angle The triangle is right-angled The other two angles are each less than 60° [4 marks] AQA Foundation: November 2017 Paper 10, Q 10 1 Might be true 1 One of the angles in a triangle is 60° Tick a box for each statement. Must be true AQA Foundation: November 2017 Paper 10, Q 10 Cannot be true One of the angles in a triangle is 60° Tick a box for each statement. Might be true The triangle is equilateral Must be true Cannot be true Might be true The triangle is equilateral The triangle is right-angled The triangle has at least one other acute angle The triangle is right-angled The other two angles are each less than 60° [4 marks]

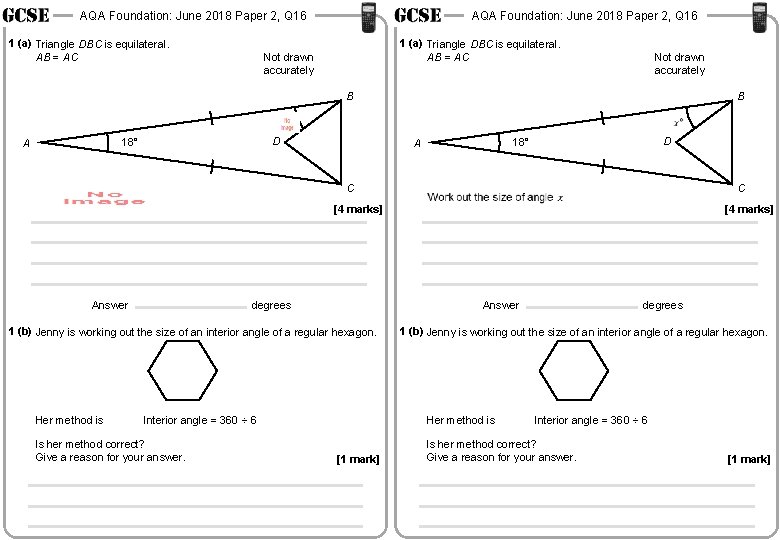
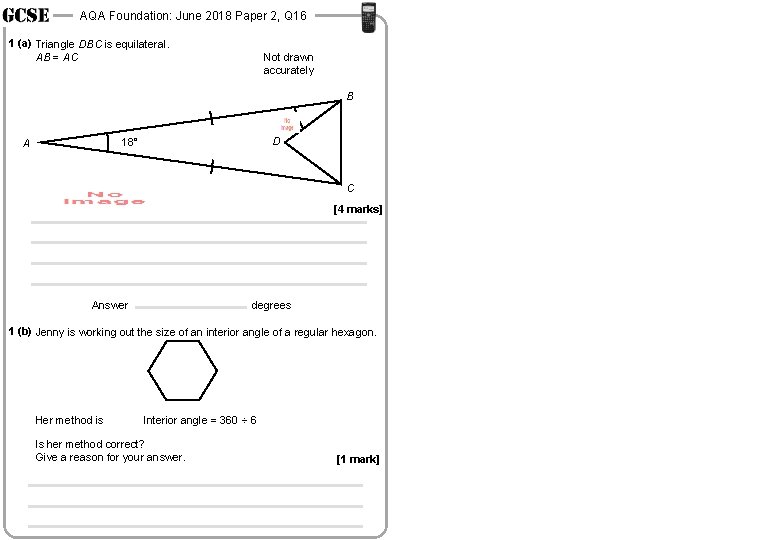
AQA Foundation: June 2018 Paper 2, Q 16 1 (a) Triangle DBC is equilateral. AB = AC Not drawn accurately B D 18° A C C [4 marks] Answer degrees Answer 1 (b) Jenny is working out the size of an interior angle of a regular hexagon. Her method is Interior angle = 360 ÷ 6 Is her method correct? Give a reason for your answer. [4 marks] 1 (b) Jenny is working out the size of an interior angle of a regular hexagon. Her method is [1 mark] degrees Interior angle = 360 ÷ 6 Is her method correct? Give a reason for your answer. [1 mark]

AQA Foundation: June 2018 Paper 2, Q 16 1 (a) Triangle DBC is equilateral. AB = AC Not drawn accurately B D 18° A C [4 marks] Answer degrees 1 (b) Jenny is working out the size of an interior angle of a regular hexagon. Her method is Interior angle = 360 ÷ 6 Is her method correct? Give a reason for your answer. [1 mark]

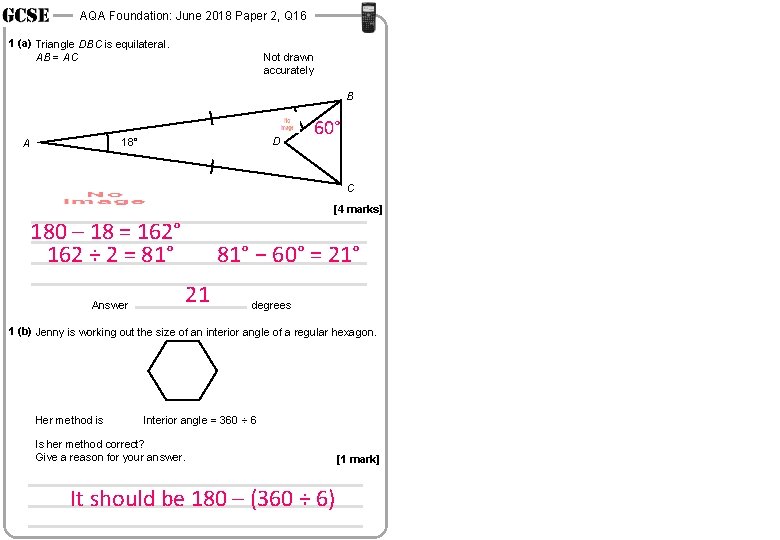
AQA Foundation: June 2018 Paper 2, Q 16 1 (a) Triangle DBC is equilateral. AB = AC Not drawn accurately B D 18° A 60° C [4 marks] 180 – 18 = 162° 162 ÷ 2 = 81° Answer 81° − 60° = 21° 21 degrees 1 (b) Jenny is working out the size of an interior angle of a regular hexagon. Her method is Interior angle = 360 ÷ 6 Is her method correct? Give a reason for your answer. It should be 180 – (360 ÷ 6) [1 mark]

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk