Ancient Egyptian Numeral System By Marvin Rosario John

Ancient Egyptian Numeral System By: Marvin Rosario & John. Michael Smith

Inventor of Egyptian Numerals Egyptians -Created roughly around 45000 BC-3500 BC (no exact date) -Used in Ancient Egypt until the early first millennium AD

Description -Base 10 -Started with written numeration that later changed into hieroglyphic writing -The signs represent people, animals, plants and numbers -Whole numbers can be written up too 1, 000

Advantages -The numeral system is base 10 but the numerals are written in their own unique ways. -It has a zero -Fractions can be done (to a limit) -Could find out area

Disadvantages -Requires a lot more space than other numeral systems -Requires a lot of time to remember each hieroglyphic -Limiting of fractions -Difficult to add numbers

Current Development The Egyptian numeral system does still play a role in current development today. The building of The Great Pyramid of Khufu from the fourth dynasty is still a mathematical wonder. It helps mathematicians develop understanding and help with building other great wonders of their own. The early examples of the Egyptian numeral system give an understanding for present philosophers.

Ancient Egyptian Hieroglyphics

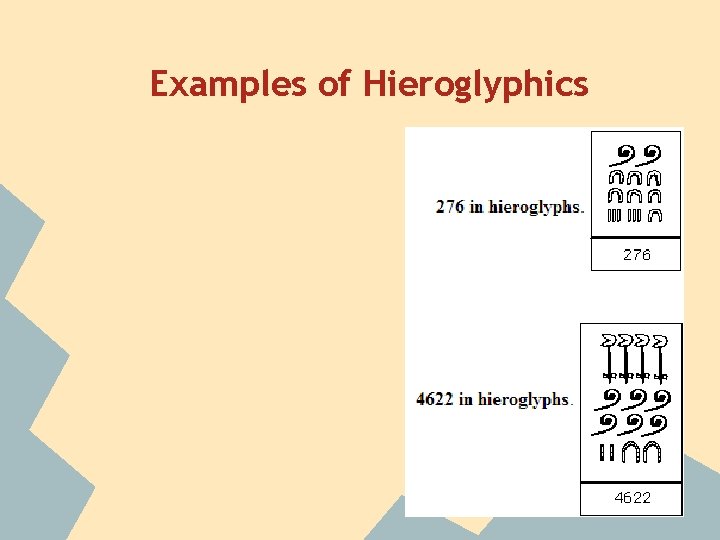
Examples of Hieroglyphics

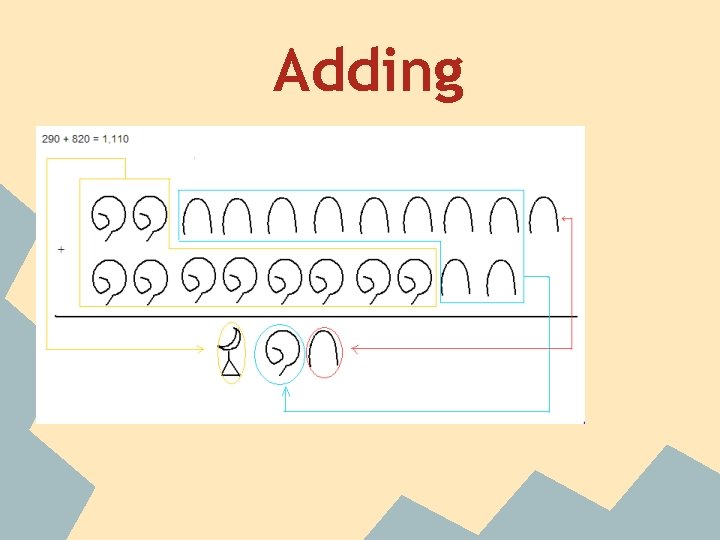
Adding

Properties for Simple Fractions • • • (*) For any n except 0, 1/n = 1/(n+1) + 1/n(n+1) (**) If n is odd, 2/n = 2/(n+1) + 2/n(n+1) = a sum of unit fractions, since 2/(n+1) and 2/n(n+1) can be reduced. (***) • (****) EXAMPLE: 2/n = 1/n + 1/(n+1) + 1/n(n+1) 1 = 1/2 + 1/3 + 1/6 2/7 = 2/8 + 2/(7*8) = 1/4 + 1/28 using (**)

Advantage of Egyptian Fractions Which is larger: 3/4 or 4/5? We could see that 3/4 =0. 75 =75/100 whereas 4/5 =0. 8 = 0. 80 = 80/100 so we can see that 80/100 is bigger than 75/100 and we can now see that 4/5 is bigger than 3/4. Using Egyptian fractions we write each as a sum of unit fractions: 3/4 = 1/2 + 1/4 4/5 = 1/2 + 3/10 and, expanding 3/10 as 1/4 + 1/20 we have 4/5 = 1/2 + 1/4 + 1/20 We can now see that 4/5 is the larger - by exactly 1/20.

A practical use of Egyptian Fractions So suppose Marvin has 5 loaves of bread to share among the 8 workers who have helped dig his fields this week and clear the irrigation channels. How would YOU approach this? First Marvin sees that they all get at least half a loaf, so he gives all 8 of them half a loaf each, with one whole loaf left. Now it is easy to divide one loaf into 8, so they get an extra eighth of a loaf each and all the loaves are divided equally between the 5 workers. They each have revieved 1/2 and 1/8 loafs of bread, and 5/8 = 1/2 + 1/8

Sources http: //www. touregypt. net/featurestories/numbers. htm http: //www. ehow. com/info_8509195_disadvantages-egyptian-numeralsystem. html#page=4 http: //www-history. mcs. st-and. ac. uk/Hist. Topics/Egyptian_mathematics. html http: //www. math. wichita. edu/history/topics/num-sys. html#egypt http: //www. mta. ca/~amiller/m 3031/The%20 Egyptian%20 Number%20 System. htm