ANALZA KONSTRUKC 5 pednka Desky n Rovinn tenkostnn

ANALÝZA KONSTRUKCÍ 5. přednáška

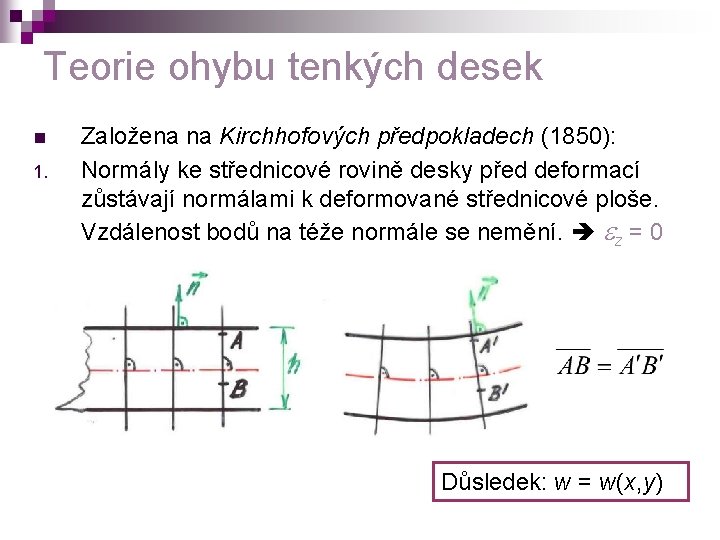
Desky n Rovinné tenkostěnné konstrukce zatížené kolmo ke své střednicové rovině Střednicová rovina – půlí vzdálenost mezi oběma povrchy

Zatížení desek n Plošné [N/m 2] n Liniové: ¨Silové [N/m] ¨Momentové [Nm/m] n Bodové ¨Silou [N] ¨Momentem [Nm]

Statické působení desek n n n Tenké desky: Kirchhoffova ohybová teorie Tlusté desky: Mindlinova teorie – je třeba uvažovat smykové přetvoření Membrány: Membránové působení – konstrukce není schopna přenášet ohybové účinky (pouze normálové síly ve střednicové rovině)

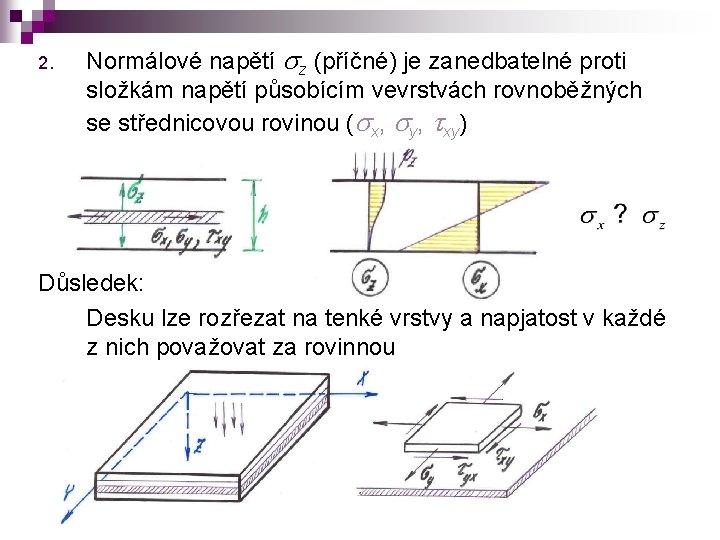
Teorie ohybu tenkých desek n 1. Založena na Kirchhofových předpokladech (1850): Normály ke střednicové rovině desky před deformací zůstávají normálami k deformované střednicové ploše. Vzdálenost bodů na téže normále se nemění. ez = 0 Důsledek: w = w(x, y)

2. Normálové napětí sz (příčné) je zanedbatelné proti složkám napětí působícím vevrstvách rovnoběžných se střednicovou rovinou (sx, sy, txy) Důsledek: Desku lze rozřezat na tenké vrstvy a napjatost v každé z nich považovat za rovinnou

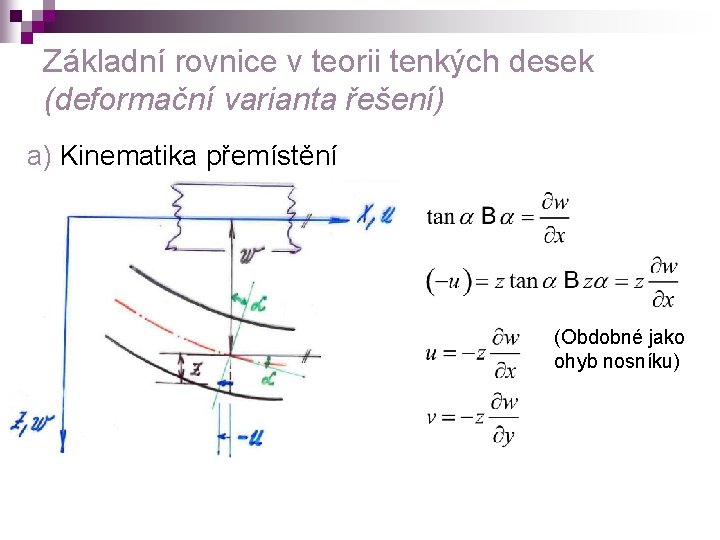
Základní rovnice v teorii tenkých desek (deformační varianta řešení) a) Kinematika přemístění (Obdobné jako ohyb nosníku)

b) Výpočet deformace c) Výpočet napětí (z fyzikálních rovnic pro rovinnou napjatost) ohybová křivost torzní křivost

Průběhy tangenciálních napětí příčných (smyk za ohybu) se dají spočítat z Cauchyho rovnic rovnováhy Integrací

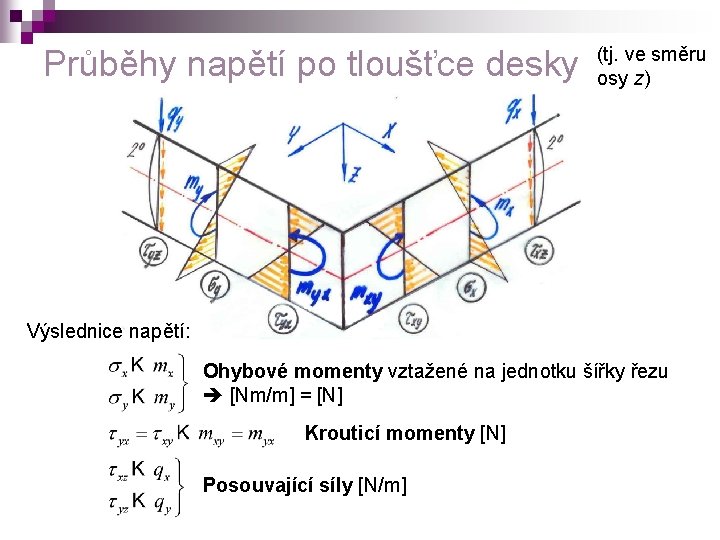
Průběhy napětí po tloušťce desky (tj. ve směru osy z) Výslednice napětí: Ohybové momenty vztažené na jednotku šířky řezu [Nm/m] = [N] Krouticí momenty [N] Posouvající síly [N/m]

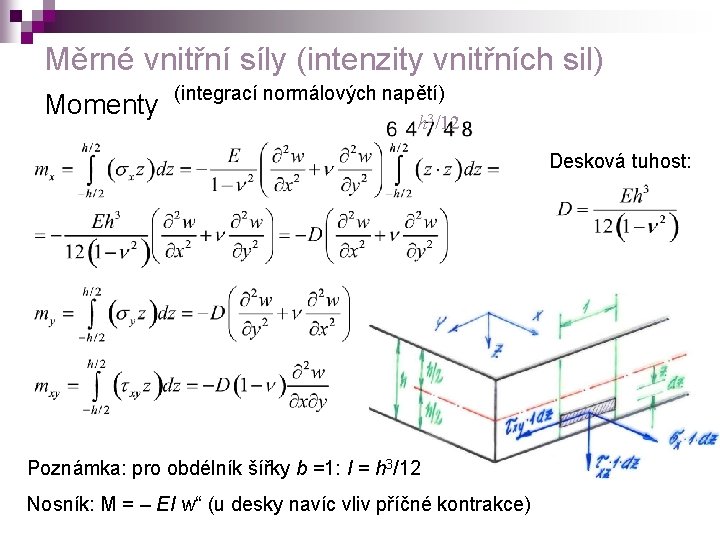
Měrné vnitřní síly (intenzity vnitřních sil) Momenty (integrací normálových napětí) h 3/12 Desková tuhost: Poznámka: pro obdélník šířky b =1: I = h 3/12 Nosník: M = – EI w“ (u desky navíc vliv příčné kontrakce)

Posouvající síly (integrací příčných tangenciálních napětí) Ačkoliv txz a tyz přímo neznáme, můžeme určit posouvající síly z momentové podmínky rovnováhy na vyjmutém elementu desky o rozměru Δx · Δy

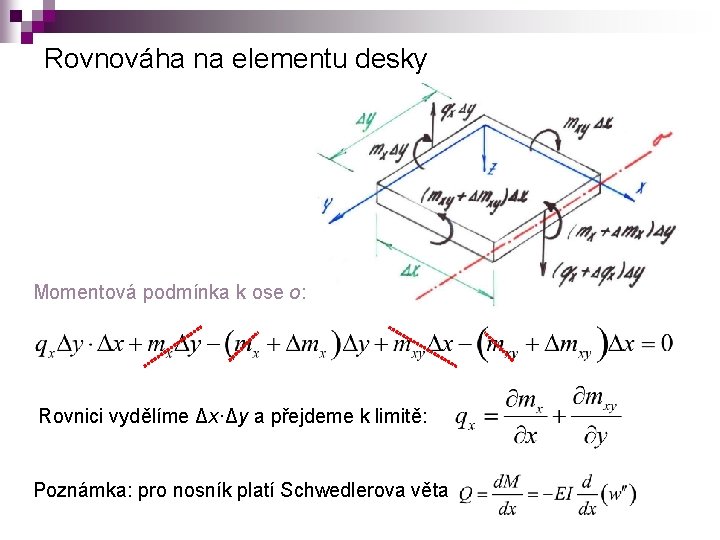
Rovnováha na elementu desky Momentová podmínka k ose o: Rovnici vydělíme Δx·Δy a přejdeme k limitě: Poznámka: pro nosník platí Schwedlerova věta

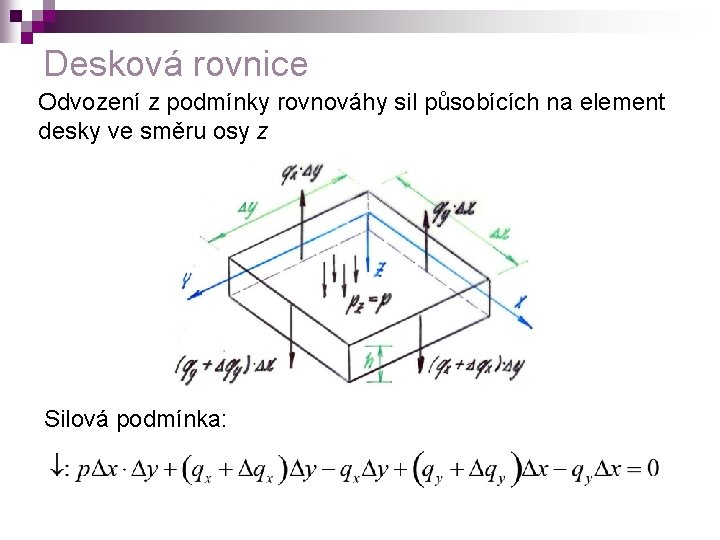
Desková rovnice Odvození z podmínky rovnováhy sil působících na element desky ve směru osy z Silová podmínka:

Rovnici vydělíme součinem ΔxΔy Desková rovnice Δ … Laplaceův operátor

Desková rovnice v rozepsaném tvaru: Nehomogenní parciální diferenciální rovnice 4. řádu Srovnání řešení stěny a desky Deska Stěna Neznámé w (průhyb) F (funkce napětí) Rovnice ΔΔw = p/D ΔΔF = 0 Význam rovnic rovnováhy kompatibility nehomogenní deformační silová Matematický tvar Metoda

Okrajové podmínky Vyjadřují způsob podepření desky Parciální diferenciální rovnici 4. řádu odpovídají 2 okrajové podmínky v každém bodě hranice a) Vetknutý okraj Okraj rovnoběžný s osou y Obecný okraj Geometrické okrajové podmínky

b) Kloubově podepřený okraj Okraj rovnoběžný s osou y Obecný okraj Geometrická podmínka Statická podmínka Upravíme na kinematický tvar:

c) Volný okraj Okraj rovnoběžný s osou y Statické okrajové podmínky Ohybový moment Posouvající síla Krouticí moment Protože na každém okraji desky lze předepsat pouze dvě okrajové podmínky, stahují se poslední dvě podmínky v podmínku jedinou, tzv. doplněnou Kirchhoffovu posouvající sílu

Okrajové podmínky na volném okraji v kinematickém tvaru: Okraj rovnoběžný s osou y Obecný okraj

Výpočet deskové rovnice metodou sítí Postup je podobný jako při řešení stěnové rovnice. Rozdíl je způsoben nenulovou pravou stranou deskové rovnice a rozdílnými okrajovými podmínkami. S ohledem na pravou stranu deskové rovnice je vhodné na čtvercové síti s krokem a zavést substitucí tzv. redukovaný průhyb W Skutečný průhyb [m] Desková rovnice: Uzlové břemeno:

Postup řešení 1) Oblast desky pokryjeme čtvercovou sítí s diferenčním krokem a 2) V každém uzlu sítě, kde neznáme průhyb (vnitřní uzly a hraniční uzly na volném okraji) sestavíme diferenční náhradu za deskovou rovnici 3) Hodnoty na hranici a mimo ni vyjádříme pomocí diferenčního vyjádření okrajových podmínek

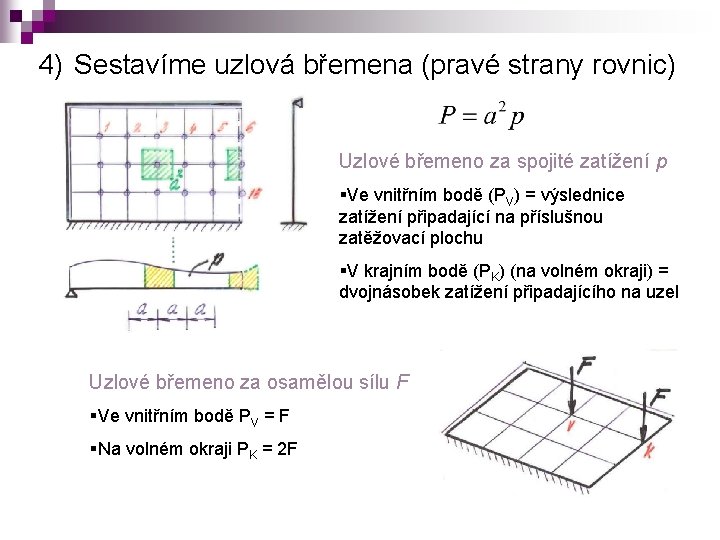
4) Sestavíme uzlová břemena (pravé strany rovnic) Uzlové břemeno za spojité zatížení p §Ve vnitřním bodě (PV) = výslednice zatížení připadající na příslušnou zatěžovací plochu §V krajním bodě (PK) (na volném okraji) = dvojnásobek zatížení připadajícího na uzel Uzlové břemeno za osamělou sílu F §Ve vnitřním bodě PV = F §Na volném okraji PK = 2 F

Diferenční vyjádření okrajových podmínek a) Vetknutý okraj 1) 2) Pro redukovaný průhyb W: Poznámka: Vetknutý okraj je v řezu jakoby osou symetrie ohybové čáry

b) Kloubově podepřený okraj 1) 2) Pro redukovaný průhyb W: Poznámka: Kloubově podepřený okraj je v řezu jakoby osou antisymetrie ohybové čáry

c) Volný okraj 1) 2) Po úpravě pro redukovaný průhyb W: Podmínka 1) v bodě 2 WA vyjádříme v závislosti na ostatních průhybech

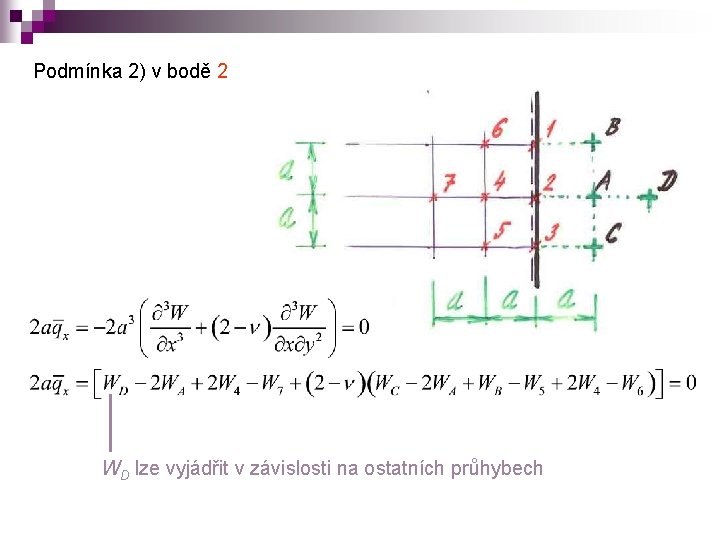
Podmínka 2) v bodě 2 WD lze vyjádřit v závislosti na ostatních průhybech

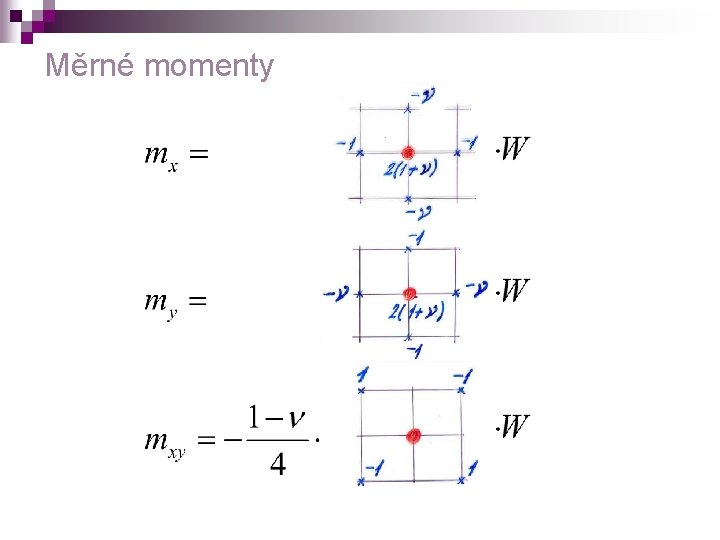
Měrné momenty

Děkuji za pozornost a těším se s vámi na shledanou za týden u testu