Analyzing Quicksort Average Case Adapted from Slides by

Analyzing Quicksort: Average Case (Adapted from Slides by David Leubke)

Review: Quicksort l Quicksort pros: n n n l Sorts in place Sorts O(n lg n) in the average case Very efficient in practice Quicksort cons: n n n Sorts O(n 2) in the worst case Naïve implementation: worst-case = sorted Even picking a different pivot, some particular input will take O(n 2) time

Review: Analyzing Quicksort l In the worst case: l In the best case: T(n) = 2 T(n/2) + (n) l Which works out to T(n) = (n lg n) T(1) = (1) T(n) = T(n - 1) + (n) l Which works out to T(n) = (n 2)

Review: Improving Quicksort The real liability of quicksort is that it runs in O(n 2) on already-sorted input l Two solutions: l n n l Randomize the input array, OR Pick a random pivot element How will these solve the problem? n n By ensuring that no particular input can be chosen to make quicksort run in O(n 2) time And multiple executions on the same input can require different amount of time

Analyzing Quicksort: Average Case Assume partition generates splits (0: n-1, 1: n-2, 2: n-3, … , n-2: 1, n-1: 0) each with probability 1/n l If T(n) is the expected running time, l What is each term under the summation for? l What is the (n) term for? l

Analyzing Quicksort: Average Case l So…

Analyzing Quicksort: Average Case l We can solve this recurrence using the dreaded substitution method n n Guess the answer Assume that the inductive hypothesis holds Substitute it in for some value < n Prove that it follows for n (Inductive Proof)

Analyzing Quicksort: Average Case l We can solve this recurrence using the dreaded substitution method n Guess the answer u T(n) n n n = O(n lg n) Assume that the inductive hypothesis holds Substitute it in for some value < n Prove that it follows for n

Analyzing Quicksort: Average Case l We can solve this recurrence using the dreaded substitution method n Guess the answer u T(n) n Assume that the inductive hypothesis holds u T(n) n n = O(n lg n) an lg n + b for some constants a and b Substitute it in for some value < n Prove that it follows for n

Analyzing Quicksort: Average Case l We can solve this recurrence using the dreaded substitution method n Guess the answer u T(n) n Assume that the inductive hypothesis holds u T(n) n an lg n + b for some constants a and b Substitute it in for some value < n u The n = O(n lg n) value k in the recurrence Prove that it follows for n

Analyzing Quicksort: Average Case The recurrence to be solved Plug What in inductive are we doing hypothesis here? Expand case Whatout arethe we k=0 doing here? Limk->0 k lg k = 0

Applying L’Hospital’s Rule

Analyzing Quicksort: Average Case The recurrence to be solved Distribute the summation What are we doing here? and simplify Evaluate the summation: What are we doing here? b+b+…+b = bn What are we doing here? This summation gets its own set of slides later

Analyzing Quicksort: Average Case The recurrence to be solved We’llthe prove this later What hell? Distribute thewe(2 a/n) What are doingterm here? Remember, our goal is to get What are we doing here? T(n) an lg n + b Pick a large enough that How did we do this? an/4 dominates (n)+b

Analyzing Quicksort: Average Case l So T(n) an lg n + b for certain a and b n n n l Thus the induction holds Thus T(n) = O(n lg n) Thus quicksort runs in O(n lg n) time on average (phew!) Oh yeah, the summation…

Tightly Bounding The Key Summation Split the summation for a What are we doing here? tighter bound The lg k in the second term What are we doing here? is bounded by lg n Move the lg n outside the What are we doing here? summation

Tightly Bounding The Key Summation The summation bound so far The lg k in the first term is What are we doing here? bounded by lg n/2 = lg n we - 1 doing here? What are Move (lg n - 1) outside the What are we doing here? summation

Tightly Bounding The Key Summation The summation bound so far Distribute the (lg nhere? - 1) What are we doing The summations overlap in What are we doing here? range; combine them The. What Guassian are weseries doing here?

Tightly Bounding The Key Summation The summation bound so far Rearrange first term, place What are we doing here? upper bound on second X Guassian What areseries we doing? Multiply it What are we doing? all out

Tightly Bounding The Key Summation

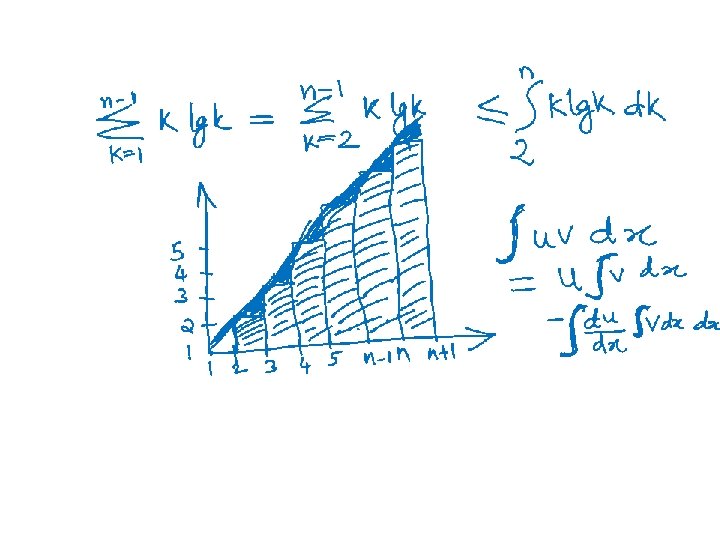
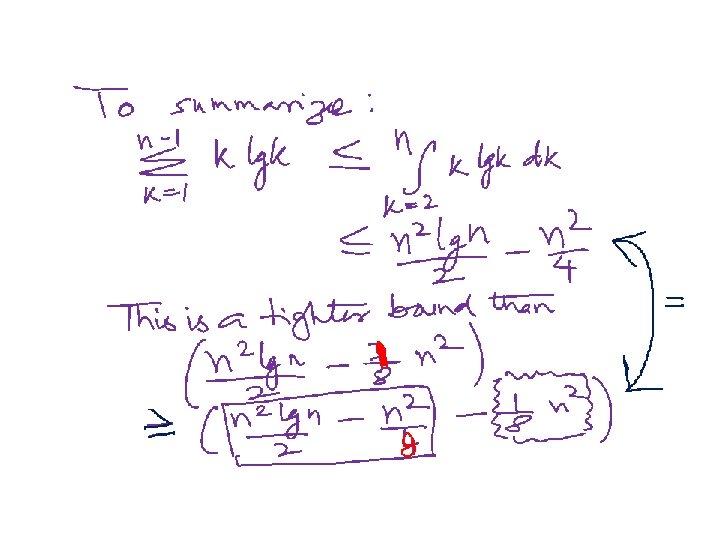
Using integration to bound sum of a series
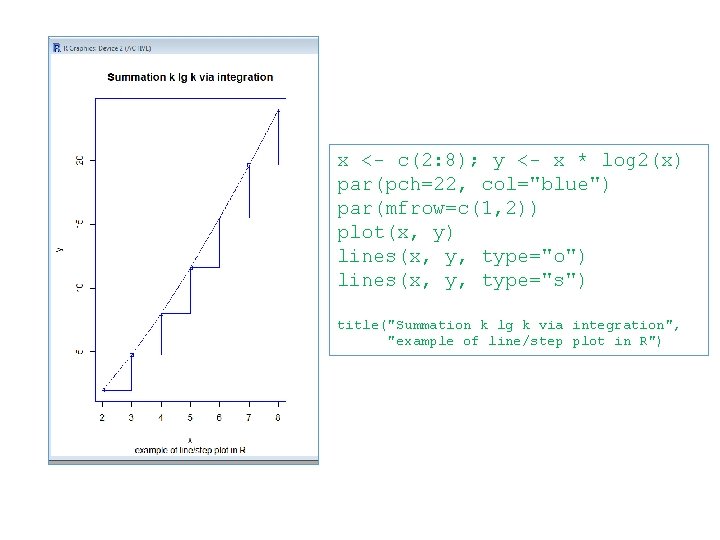
x <- c(2: 8); y <- x * log 2(x) par(pch=22, col="blue") par(mfrow=c(1, 2)) plot(x, y) lines(x, y, type="o") lines(x, y, type="s") title("Summation k lg k via integration", "example of line/step plot in R")
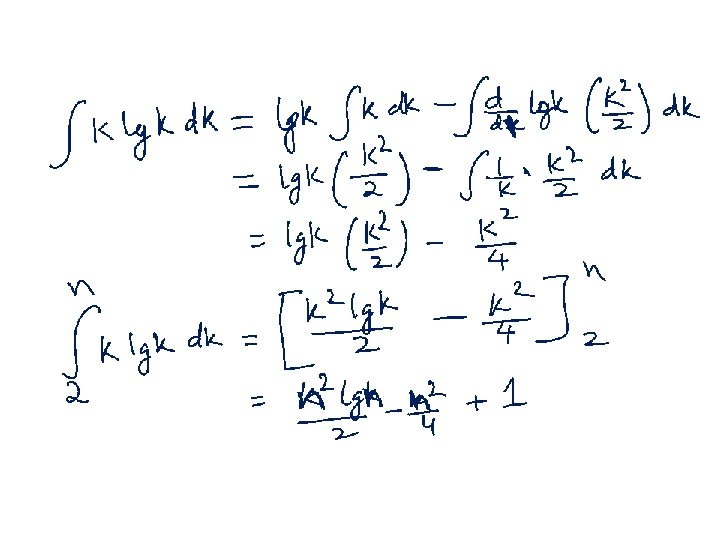
- Slides: 25