Analyzing OneVariable Data Lesson 1 8 Summarizing Quantitative

Analyzing One-Variable Data Lesson 1. 8 Summarizing Quantitative Data: Boxplots and Outliers Statistics and Probability with Applications, 3 rd Edition Starnes & Tabor Bedford Freeman Worth Publishers

Boxplots and Outliers Learning Targets After this lesson, you should be able to: ü Use the 1. 5 x IQR rule to identify outliners. ü Make and interpret boxplots of quantitative data. ü Compare distributions of quantitative data with boxplots. Statistics and Probability with Applications, 3 rd Edition 2

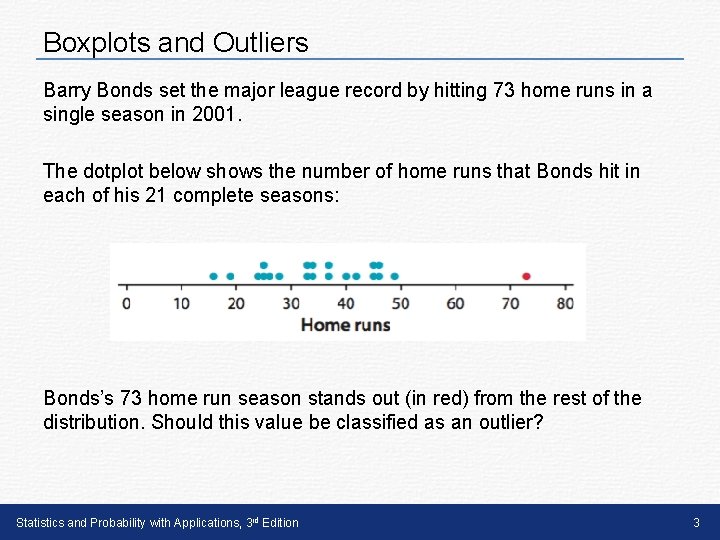
Boxplots and Outliers Barry Bonds set the major league record by hitting 73 home runs in a single season in 2001. The dotplot below shows the number of home runs that Bonds hit in each of his 21 complete seasons: Bonds’s 73 home run season stands out (in red) from the rest of the distribution. Should this value be classified as an outlier? Statistics and Probability with Applications, 3 rd Edition 3

Boxplots and Outliers Besides serving as a measure of variability, the interquartile range (IQR) is used as a ruler for identifying outliers. The 1. 5 x IQR Rule Call an observation an outlier if it falls more than 1. 5 × IQR above third quartile or below the first quartile. That is, Low Outliers < Q 1 − 1. 5 × IQR High Outliers > Q 3 + 1. 5 × IQR Statistics and Probability with Applications, 3 rd Edition 4

To Determine Outliers Find Quartile 1 & Quartile 3 Determine Interquartile Range : IQR = Q 3 - Q 1 Multiply 1. 5 x IQR Set up “fences” Q 1 -(1. 5 IQR) and Q 3+(1. 5 IQR) Observations “outside” the fences are outliers. Statistics and Probability with Applications, 3 rd Edition 5

6 IDENTIFYING OUTLIERS • USE THE 1. 5 IQR RULE TO DECIDE IF THERE ANY OUTLIERS IN THE FOLLOWING DATA SET: 17 23 24 27 32 35 16 70 12 15 22 35 34 18 0 Find Quartile 1 & Quartile 3 Determine Interquartile Range : IQR = Q 3 - Q 1 Multiply 1. 5 x IQR Set up “fences” Q 1 -(1. 5 IQR) and Q 3+(1. 5 IQR) Observations “outside” the fences are outliers. Statistics and Probability with Applications, 3 rd Edition 6

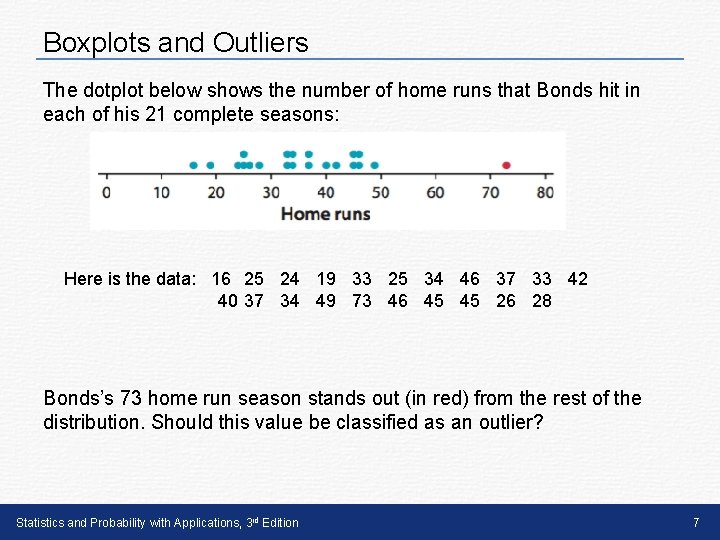
Boxplots and Outliers The dotplot below shows the number of home runs that Bonds hit in each of his 21 complete seasons: Here is the data: 16 25 24 19 33 25 34 46 37 33 42 40 37 34 49 73 46 45 45 26 28 Bonds’s 73 home run season stands out (in red) from the rest of the distribution. Should this value be classified as an outlier? Statistics and Probability with Applications, 3 rd Edition 7

Boxplots and Outliers It is important to identify outliers in a distribution for several reasons: 1. They might be inaccurate data values. 2. They can indicate a remarkable occurrence. 3. They can heavily influence the values of some summary statistics, like the mean, range, and standard deviation. Statistics and Probability with Applications, 3 rd Edition 8

Boxplots and Outliers You can use a dotplot, stemplot, or histogram to display the distribution of a quantitative variable. Another graphical option for quantitative data is a boxplot (sometimes called a box-and-whisker plot). A boxplot summarizes a distribution by displaying the location of 5 important values within the distribution, known as its five-number summary. Five-Number Summary, Boxplot The five-number summary of a distribution of quantitative data consists of the minimum, the first quartile Q 1, the median, the third quartile Q 3, and the maximum. A boxplot is a visual representation of the five-number summary. Statistics and Probability with Applications, 3 rd Edition 9

. 1 0 USING THE CALCULATOR • TO FIND THE 5 -NUMBER SUMMARY ON THE CALCULATOR: 1. ENTER DATA INTO A LIST 2. USING THE STAT MENU SCROLL TO STAT AND RUN 1 -VARS STATS ON LIST Find the 5 -number summary for the data list: 7 18 11 6 59 17 18 54 104 20 31 8 10 15 Statistics and Probability with Applications, 3 rd Edition 10

Box-and-Whisker Plot • Exploratory data analysis tool. • Highlights important features of a data set. • Requires (five-number summary): – Minimum entry – First quartile Q 1 – Median Q 2 – Third quartile Q 3 – Maximum entry Box Whisker Minimum entry rd Edition © 2012 and Pearson Education, Inc. All rights 3 reserved. Statistics Probability with Applications, Whisker Q 1 Median, Q 2 Q 3 Maximum entry 11 of 149 11

Drawing a Box-and-Whisker Plot 1. Find the five-number summary of the data set. 2. Construct a horizontal scale that spans the range of the data. 3. Plot the five numbers above the horizontal scale. 4. Draw a box above the horizontal scale from Q 1 to Q 3 and draw a vertical line in the box at Median. 5. Draw whiskers from the box to the minimum and maximum entries if there are no outliers. Box Whisker Minimum entry Whisker Q 1 rd Edition © 2012 and Pearson Education, Inc. All rights 3 reserved. Statistics Probability with Applications, Median, Q 2 Q 3 Maximum entry 12 of 14 12

Example: Drawing a Box-and-Whisker Plot Draw a box-and-whisker plot that represents 15 test scores with the following summary statistics: Min = 5 Q 1 = 10 Q 2 = 15 Q 3 = 18 Max = 37 Solution: 5 10 15 18 37 About half the scores are between 10 and 18. By looking at the length of the right whisker, you can conclude 37 is a possible outlier. Larson/Farber 4 th ed. with Applications, 3 rd Edition Statistics and Probability 1313

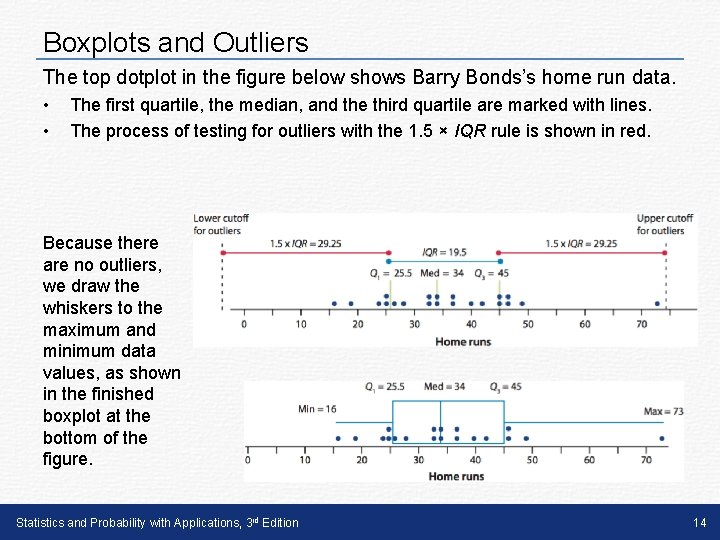
Boxplots and Outliers The top dotplot in the figure below shows Barry Bonds’s home run data. • • The first quartile, the median, and the third quartile are marked with lines. The process of testing for outliers with the 1. 5 × IQR rule is shown in red. Because there are no outliers, we draw the whiskers to the maximum and minimum data values, as shown in the finished boxplot at the bottom of the figure. Statistics and Probability with Applications, 3 rd Edition 14

Modified Boxplots • display outliers • fences mark off mild & extreme outliers • whiskers extend to largest ALWAYS use (smallest) data value inside modified boxplots in the fence this class!!! Statistics and Probability with Applications, 3 rd Edition 15

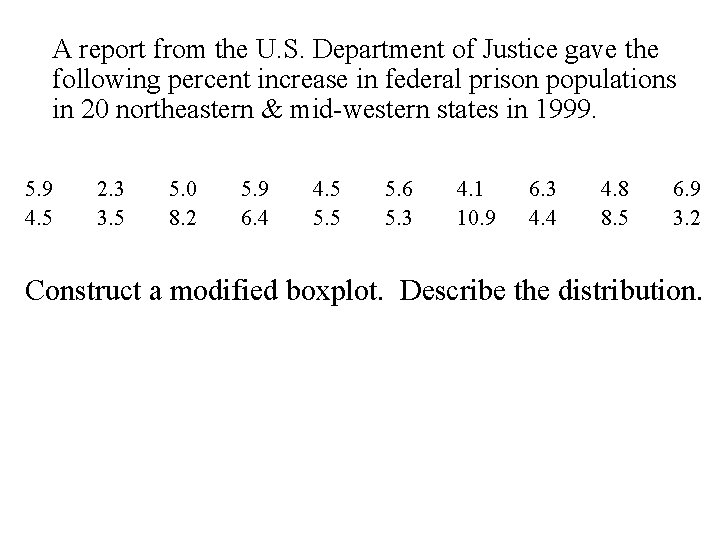
A report from the U. S. Department of Justice gave the following percent increase in federal prison populations in 20 northeastern & mid-western states in 1999. 5. 9 4. 5 2. 3 3. 5 5. 0 8. 2 5. 9 6. 4 4. 5 5. 6 5. 3 4. 1 10. 9 6. 3 4. 4 4. 8 8. 5 6. 9 3. 2 Construct a modified boxplot. Describe the distribution.

Why use boxplots? • ease of construction • convenient handling of outliers • Used with medium or large size data sets (n > 10) • useful for comparative displays

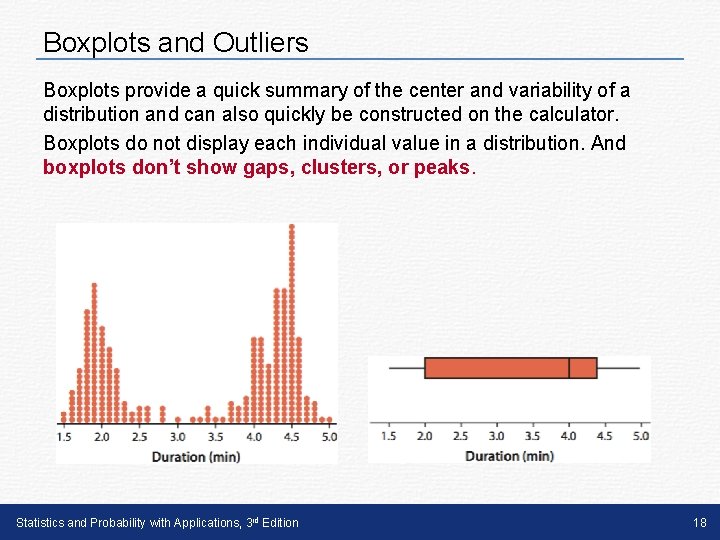
Boxplots and Outliers Boxplots provide a quick summary of the center and variability of a distribution and can also quickly be constructed on the calculator. Boxplots do not display each individual value in a distribution. And boxplots don’t show gaps, clusters, or peaks. Statistics and Probability with Applications, 3 rd Edition 18

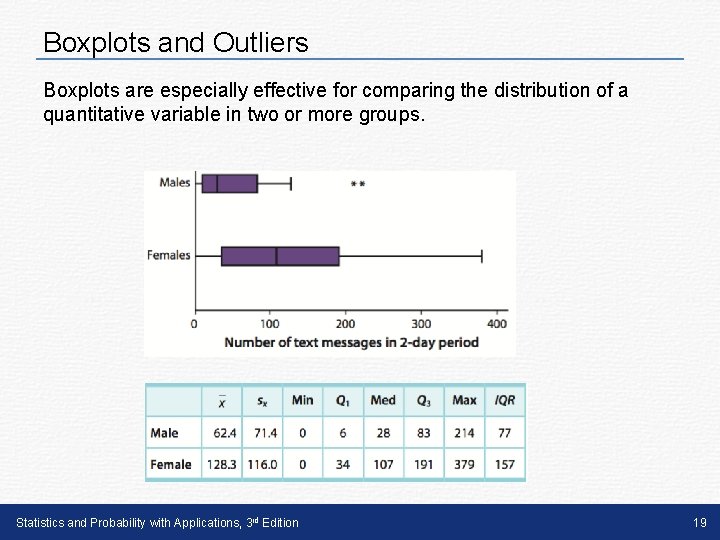
Boxplots and Outliers Boxplots are especially effective for comparing the distribution of a quantitative variable in two or more groups. Statistics and Probability with Applications, 3 rd Edition 19

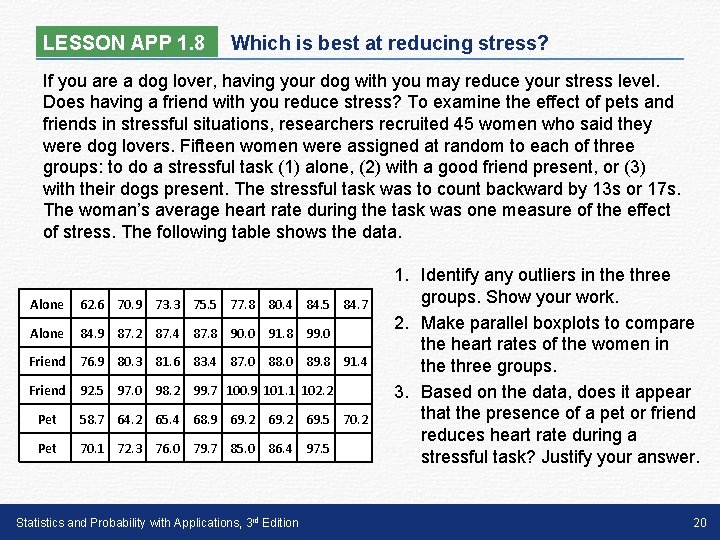
LESSON APP 1. 8 Which is best at reducing stress? If you are a dog lover, having your dog with you may reduce your stress level. Does having a friend with you reduce stress? To examine the effect of pets and friends in stressful situations, researchers recruited 45 women who said they were dog lovers. Fifteen women were assigned at random to each of three groups: to do a stressful task (1) alone, (2) with a good friend present, or (3) with their dogs present. The stressful task was to count backward by 13 s or 17 s. The woman’s average heart rate during the task was one measure of the effect of stress. The following table shows the data. Alone 62. 6 70. 9 73. 3 75. 5 77. 8 80. 4 84. 5 84. 7 Alone 84. 9 87. 2 87. 4 87. 8 90. 0 91. 8 99. 0 Friend 76. 9 80. 3 81. 6 83. 4 87. 0 88. 0 89. 8 91. 4 Friend 92. 5 97. 0 98. 2 99. 7 100. 9 101. 1 102. 2 Pet 58. 7 64. 2 65. 4 68. 9 69. 2 69. 5 70. 2 Pet 70. 1 72. 3 76. 0 79. 7 85. 0 86. 4 97. 5 Statistics and Probability with Applications, 3 rd Edition 1. Identify any outliers in the three groups. Show your work. 2. Make parallel boxplots to compare the heart rates of the women in the three groups. 3. Based on the data, does it appear that the presence of a pet or friend reduces heart rate during a stressful task? Justify your answer. 20

Boxplots and Outliers Learning Targets After this lesson, you should be able to: ü Use the 1. 5 × IQR rule to identify outliners. ü Make and interpret boxplots of quantitative data. ü Compare distributions of quantitative data with boxplots. Statistics and Probability with Applications, 3 rd Edition 21