Analyzing OneVariable Data Lesson 1 7 Measuring Variability

Analyzing One-Variable Data Lesson 1. 7 Measuring Variability Statistics and Probability with Applications, 3 rd Edition Starnes, Tabor Bedford Freeman Worth Publishers

Measuring Variability Learning Targets After this lesson, you should be able to: ü Find the range of a distribution of quantitative data. ü Find and interpret the interquartile range. ü Calculate and interpret the standard deviation. Statistics and Probability with Applications, 3 rd Edition 2

Measures of Spread: Standard Deviation Measures of central tendency identify the “center” or “typical value” of the data. Find the mean of each of the following sets of numbers. 50, 58, 78, 81, 93 72, 71, 72, 73 Although, the means are the same, would you say that the two data sets describe similar sets of data? Rather, the first data set shows more variability than the second. Measures of spread (also called measures of dispersion) describe the spread or variability of the data around a central value. Statistics and Probability with Applications, 3 rd Edition 3

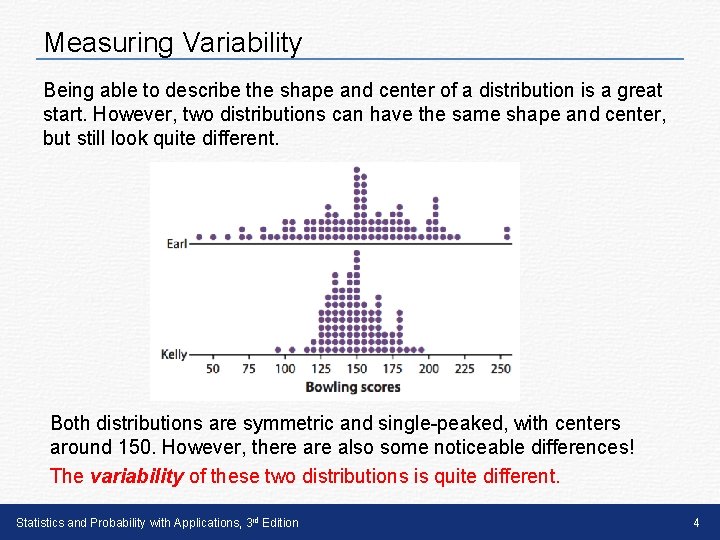
Measuring Variability Being able to describe the shape and center of a distribution is a great start. However, two distributions can have the same shape and center, but still look quite different. Both distributions are symmetric and single-peaked, with centers around 150. However, there also some noticeable differences! The variability of these two distributions is quite different. Statistics and Probability with Applications, 3 rd Edition 4

How Spread Out is the Distribution? • Variation matters, and Statistics is about variation. • Are the values of the distribution tightly clustered around the center or more spread out? • Always report a measure of spread along with a measure of center when describing a distribution numerically. Slide 4 - 5 Statistics and Probability with Applications, 3 rd Edition 5

Measuring Variability There are several ways to measure the variability of a distribution. The three most common are the range, interquartile range, and standard deviation. Range The range of a distribution is the distance between the minimum value and the maximum value. That is, Range = Maximum - Minimum The range is not a resistant measure of variability. It depends only on the maximum and minimum values, which may be outliers. Statistics and Probability with Applications, 3 rd Edition 6

Measuring Variability We can avoid the impact of extreme values on our measure of variability by focusing on the middle of the distribution. • Order the data values from smallest to largest. • Find the quartiles, the values that divide the distribution into four groups of roughly equal size. • The first quartile Q 1 lies one-quarter of the way up the list. • The second quartile is the median, which is halfway up the list. • The third quartile Q 3 lies three-quarters of the way up the list. Statistics and Probability with Applications, 3 rd Edition 7

Measuring Variability Quartiles The quartiles of a distribution divide the ordered data set into four groups having roughly the same number of values. To find the quartiles, arrange the data values from smallest to largest and find the median. The first quartile Q 1 is the median of the data values that are to the left of the median in the ordered list. The third quartile Q 3 is the median of the data values that are to the right of the median in the ordered list. Statistics and Probability with Applications, 3 rd Edition 8

Measuring Variability The interquartile range (IQR) measures the variability in the middle half of the distribution. Interquartile Range (IQR) The interquartile range (IQR) is the distance between the first and third quartiles of a distribution. In symbols, IQR = Q 3 − Q 1 The quartiles and the interquartile range are resistant because they are not affected by a few extreme values. Statistics and Probability with Applications, 3 rd Edition 9

FINDING QUARTILES • Listed below are the lengths of the touchdown passes for the Green Bay Packers over the course of several games 28, 18, 20, 32, 27, 32, 20, 22, 31, 35, 39, 33, 19, 18 Find Q 1, the median, and Q 3 and explain what these values tell about the distribution Slide 4 - and 10 Probability with Applications, 3 rd Edition Statistics 10

THE IQR • The difference between the quartiles is the interquartile range (IQR), so IQR = upper quartile – lower quartile OR Q 3 - Q 1 Find the IQR of the Green Bay data and write a sentence explaining the meaning of this value. Slide 4 - and 11 Probability with Applications, 3 rd Edition Statistics 11

Measuring Spread: The Standard Deviation When we use the mean as our measure of center, we need another measure of spread. The most common measure of spread looks at how far each observation is from the mean. This measure is called the standard deviation. Consider the following data on the number of pets owned by a group of 9 children. 1) Calculate the mean. 2) Calculate each deviation = observation – mean deviation: 1 - 5 = - 4 deviation: 8 - 5 = 3 =5 Statistics and Probability with Applications, 3 rd Edition 12

Measuring Spread: The Standard Deviation 3) Square each deviation. 4) Find the “average” squared deviation. Calculate the sum of the squared deviations divided by (n-1)…this is called the variance. 5) Calculate the square root of the variance…this is the standard deviation. xi (xi-mean) 1 1 - 5 = -4 (-4)2 = 16 3 3 - 5 = -2 (-2)2 = 4 4 4 - 5 = -1 (-1)2 = 1 5 5 -5=0 (0)2 = 0 7 7 -5=2 (2)2 = 4 8 8 -5=3 (3)2 = 9 9 9 -5=4 (4)2 = 16 Sum=? “average” squared deviation = 52/(9 -1) = 6. 5 (xi-mean)2 Sum=? This is the variance. Standard deviation = square root of variance = Statistics and Probability with Applications, 3 rd Edition 13

Measuring Spread: The Standard Deviation The standard deviation sx measures the average distance of the observations from their mean. It is calculated by finding an average of the squared distances and then taking the square root. The average squared distance is called the variance. df Statistics and Probability with Applications, 3 rd Edition 14

Using Technology to Find the Standard Deviation Larson/Farber 4 th ed. with Applications, 3 rd Edition Statistics and Probability 1515

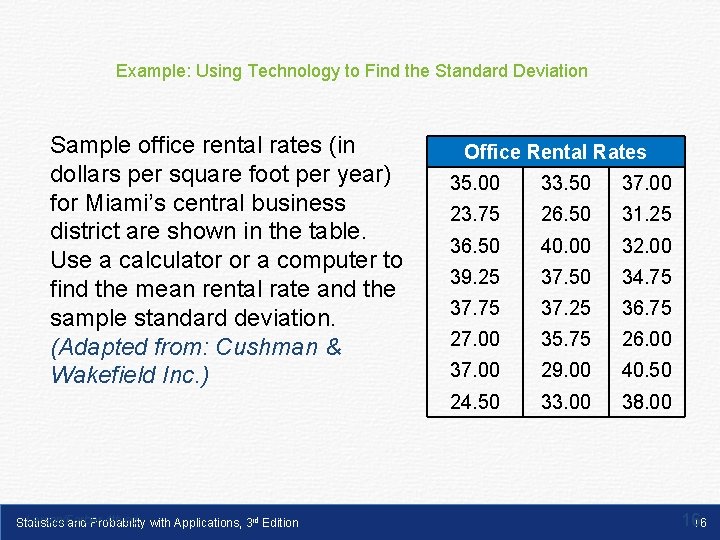
Example: Using Technology to Find the Standard Deviation Sample office rental rates (in dollars per square foot per year) for Miami’s central business district are shown in the table. Use a calculator or a computer to find the mean rental rate and the sample standard deviation. (Adapted from: Cushman & Wakefield Inc. ) Larson/Farber 4 th ed. with Applications, 3 rd Edition Statistics and Probability Office Rental Rates 35. 00 33. 50 37. 00 23. 75 26. 50 31. 25 36. 50 40. 00 32. 00 39. 25 37. 50 34. 75 37. 25 36. 75 27. 00 35. 75 26. 00 37. 00 29. 00 40. 50 24. 50 33. 00 38. 00 1616

Measuring Variability Properties of the standard deviation as a measure of variability: • sx is always greater than or equal to 0. sx = 0 only when there is no variability, that is, when all values in a distribution are the same. • Larger values of sx indicate greater variation from the mean of a distribution. • sx is not resistant. The use of squared deviations makes sx even more sensitive than x to extreme values in a distribution. • sx measures variation about the mean. It should be used only when the mean is chosen as the measure of center. Statistics and Probability with Applications, 3 rd Edition 17

S l i d e Interpreting Standard Deviation 4 1 8 • Standard deviation is a measure of the typical amount an entry deviates from the mean. • The more the entries are spread out, the greater the standard deviation. Larson/Farber 4 th ed. with Applications, 3 rd Edition Statistics and Probability 1818

S l i d e 4 1 9 Thinking About Variation • Since Statistics is about variation, spread is an important fundamental concept of Statistics. • Measures of spread help us talk about what we don’t know. • When the data values are tightly clustered around the center of the distribution, the IQR and standard deviation will be small. • When the data values are scattered far from the center, the IQR and standard deviation will be large. Statistics and Probability with Applications, 3 rd Edition 19

Measuring Variability Choosing Measures of Center and Variability The median and IQR are usually better than the mean and standard deviation for describing a skewed distribution or a distribution with outliers. Use the mean and sx only for roughly symmetric distributions that don’t have outliers. Statistics and Probability with Applications, 3 rd Edition 20

LESSON APP 1. 7 Have we found the beef? Here are data on the amount of fat (in grams) in 12 different Mc. Donald’s beef sandwiches, along with a dotplot. The mean fat content for these sandwiches is x-bar = 22. 833 grams. 27 11 22 21 40 1. 2. 3. 4. 8 17 15 29 31 27 26 Find the range of the distribution. Find the interquartile range. Interpret this value in context. Calculate the standard deviation. Interpret this value in context. The dotplot suggests that the Bacon Clubhouse Burger, with its 40 g of fat, is a possible outlier. Recalculate the range, interquartile range, and standard deviation for the other 11 sandwiches. Compare these values with the ones you obtained in Questions 1 through 3. Explain why each result makes sense. Statistics and Probability with Applications, 3 rd Edition 21

Measuring Variability Learning Targets After this lesson, you should be able to: ü Find the range of a distribution of quantitative data. ü Find and interpret the interquartile range. ü Calculate and interpret the standard deviation. Statistics and Probability with Applications, 3 rd Edition 22