Analyzing and Characterizing SmallWorld Graphs Van Nguyen and

Analyzing and Characterizing Small-World Graphs Van Nguyen and Chip Martel Computer Science, UC Davis 1

Contents Small-world phenomenon & Models The diameter of Kleinberg’s grid A Framework for Small-world graphs 2

Small-world phenomenon Two strangers meet and discover that they are two ends of a short chain of acquaintances Boston Nebraska Milgram’s pioneering work (1967): “six degrees of separation between any two Americans” n n Source person in Nebraska, target at person in Boston Chained people supposed to forward to someone they knew based on a first-name basis Here, we often use `small-world graphs’ for graphs with small diameter (poly-log functions of size) 3

Modeling Small-Worlds Many networks are Small-Worlds (e. g. WWW, Internet AS) Motivated models of small-worlds: (Watts-Strogatz, Kleinberg) New Analysis and Algorithms Applications n peer-to-peer systems n gossip protocols n secure distributed protocols n 4

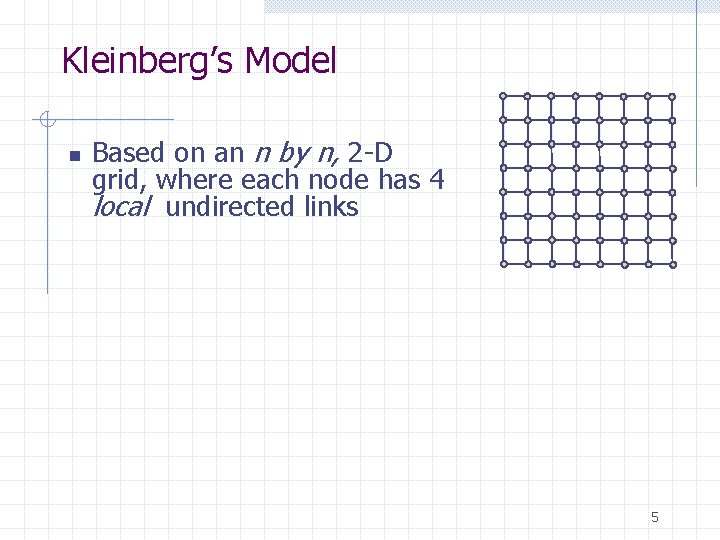
Kleinberg’s Model n Based on an n by n, 2 -D grid, where each node has 4 local undirected links 5

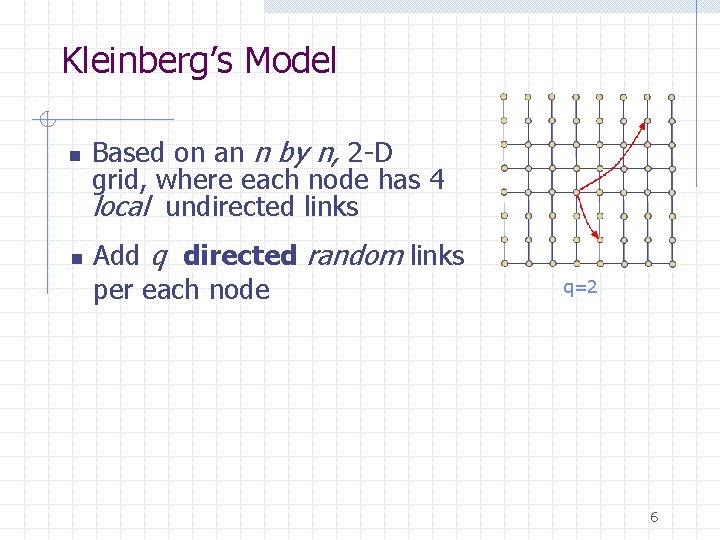
Kleinberg’s Model n n Based on an n by n, 2 -D grid, where each node has 4 local undirected links Add q directed random links per each node q=2 6

Kleinberg’s Model n n Based on an n by n, 2 -D grid, where each node has 4 local undirected links Add q directed random links per each node where w Define d(u, v): lattice distance between u and v u v d(u, v)=2+5=7 w Now, u has a link to v with probability -r proportional to d (u, v). Parameter r determines crucial behaviors of the model. 7

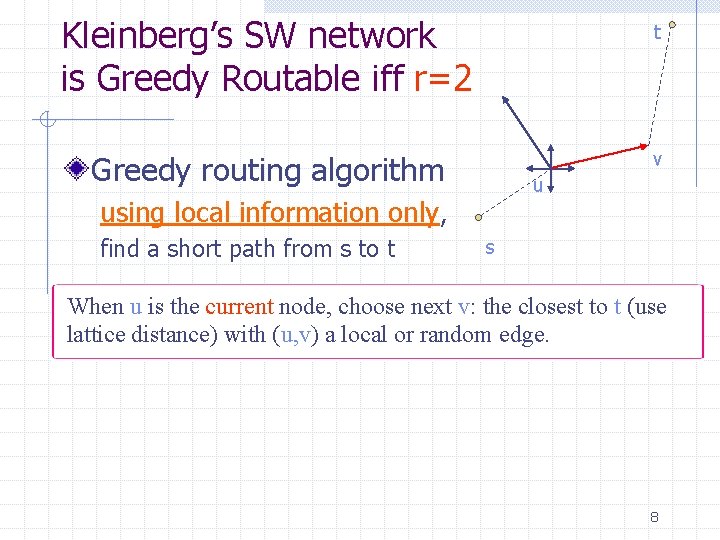
Kleinberg’s SW network is Greedy Routable iff r=2 t Greedy routing algorithm v u using local information only, find a short path from s to t s When u is the current node, choose next v: the closest to t (use lattice distance) with (u, v) a local or random edge. 8

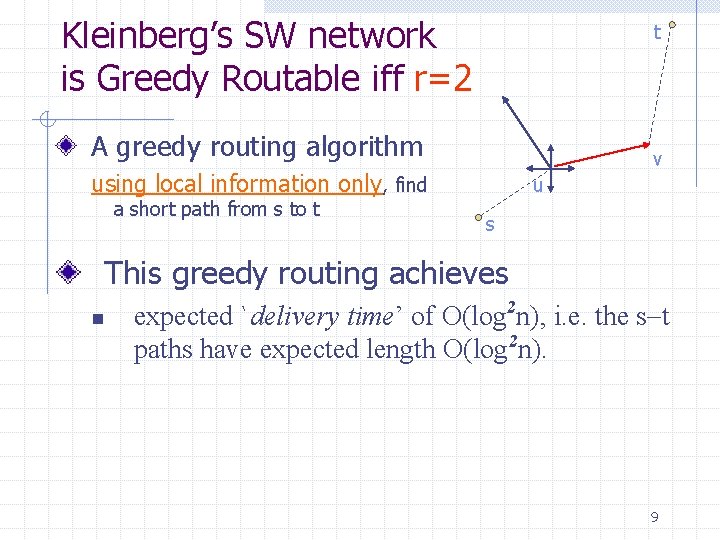
Kleinberg’s SW network is Greedy Routable iff r=2 t A greedy routing algorithm v using local information only, find a short path from s to t u s This greedy routing achieves n expected `delivery time’ of O(log 2 n), i. e. the s t paths have expected length O(log 2 n). 9

Kleinberg’s SW network is Greedy Routable iff r=2 t A greedy routing algorithm v using local information only, find a short path from s to t u s This greedy routing achieves n n expected `delivery time’ of O(log 2 n), i. e. the s t paths have expected length O(log 2 n). This does not work unless r=2 : for r 2, >0 such that the expected delivery time of any decentralized algorithm is (n ). 10

Our Results An analysis of the expected diameter of Kleinberg's setting. For a 2 D-grid, One random link/node (q=1) n If 0 r 2: diameter= (logn) – PODC’ 04 11

Our Results An analysis of the expected diameter of Kleinberg's setting. For a 2 D-grid, One random link/node (q=1) n If 0 r 2: diameter= (logn) – PODC’ 04 c log n for c>1 c n If 4< r: diameter > n for 0<c<1 n If 2< r <4: diameter < 12

Our Results An analysis of the expected diameter of Kleinberg's setting. For a 2 D-grid, One random link/node (q=1) If 0 r 2: diameter= (logn) – PODC’ 04 c n If 2< r <4: diameter <log n for c>1 c n If 4< r: diameter> n for 0<c<1 n Can be generalized for k-D grid, say if c k< r <2 k: diameter < log n for c>1 13

Our Results A framework to construct classes of random graphs with (logn) expected diameter n n We start with a general framework where random arcs are added to a fixed base graph. Then we refine this setting additional properties. A more refined class of random graphs where with local information only we find paths of expected poly-log length. 14

Prior work on similar (diameter) problems Diameter of a cycle plus a random matching: Bollobas & Chung, 88 n Can be seen as a special case of Kleinberg’s grid setting where: 1 -D lattice, undirected graph, r=0 (random links are uniform) Diameter of long-range percolation graphs n n n Benjamini & Berger, 2001 Coppersmith et al. , 2002 Biskup, 2004: similar to our approach 15

The diameter of Kleinberg’s SW setting For simplicity, use a 1 -D setting Define C(r, n) as an n-node cycle. . n Each node has 2 local links and n One directed random-link: i is connected to j i with Pr[i j] ~ |i-j|-r . . n-1 0 1 2 . . . j i For 0 r 1, we showed the diameter is (logn) in PODC’ 04 Now consider r>1. 16

Upper bound for the diameter of C(r, n) when 1<r<2 We use a probabilistic recurrence approach n n Our approach is similar to Karp's (STOC’ 91) We establish a (probabilistic) relation between the diameter of a segment and that of a smaller one. 17

Upper bound for the diameter of C(r, n) when 1<r<2 n We use a (probabilistic) relation between the diameter of a segment and a sub-segment. w. We relate D(x) , the diameter of a segment of length x, to D(y) , where y=xa for some a (0, 1). w. Intuitively, w. h. p, D(x) is bounded by a constant multiple of D(y). 18

Upper bound for the diameter of C(r, n) when 1<r<2 w Iterating the relation, starting with x=n, standard recurrence techniques bound D(n) the graph's expected diameter - based on D(x 0) for some x 0 small enough (a poly-log function of n). D(n) D(na 2) … D(x 0) 19

Partitioning Hierarchy Partitioning: A segment of length x is divided into multiple sub-segments of length a for a (0, 1). y=x 20

Partitioning Hierarchy Partitioning n n A segment of length x is divided into multiple sub -segments of length y=x a for some a (0, 1). A B A partition is complete when every pair of sub-segments has two random directed edges connecting one to the other. 21

Partitioning Hierarchy D(n) D(na 2) … We iterate this partitioning from x=n to some small x 0 (for fixed a). We need to specify y (or a) D(x 0) s. t. n n Small enough # iterations is order loglog (n) Not too small Almost surely, each phase’s partition is complete 22

Supporting Facts Fact 1: For a fixed a s. t. r/2< a <1 and for x large enough, almost surely, all partitions of length x segments are complete n n Note: 0<r<1 and y=x a Implies that all sub-segments are large enough so can get to another by one link. 23

Supporting Facts Fact 2: If a partition of a segment of length x is complete, then almost surely D(x) is at most twice the maximum diameter of a subsegment, plus 1. n Basically, any shortest path s t can be upper bounded by two shortest paths within a sub-segment plus 1 u s * A v w* t u+x-1 B length(s t) length(s v)+length(w t)+1 for (v, w) 2 max D(y) +1 24

Supporting Facts Fact 2: If a partition of a segment of length x is complete, then almost surely D(x) is at most twice the maximum diameter of a sub-segment, plus 1. Fact 2 still true if we redefine D(x) as the maximum value of the diameters of all segments of length x 25

Poly-log diameter for 1 r 2 Consider the sequence of maximum diameter values in our partitioning hierarchy D(n), D(na), … , D(x 0) D(x) 2 D(x a)+1 n The # of terms is (loglog n) Where almost surely, D(x 0) x 0, bounded by a poly-log(n) So, D(n)= O(logcn) for c>0 depending on r only n 26

The diameter of C(r, n) For r>2, C(r, n) is a ‘large’ world r-1 c expected diameter (n ), c= /r w Random links tend to go to close nodes Few long links 27

Higher dimensions We generalize to k-dimensional grids If 0 r k: diameter= (logn) c n If k< r <2 k: diameter < log n , c>1 c n If 2 k< r: diameter> n for 0<c<1 The case r=2 k is still open. n Also generalized for Growth Restricted Graphs (mention more later) 28

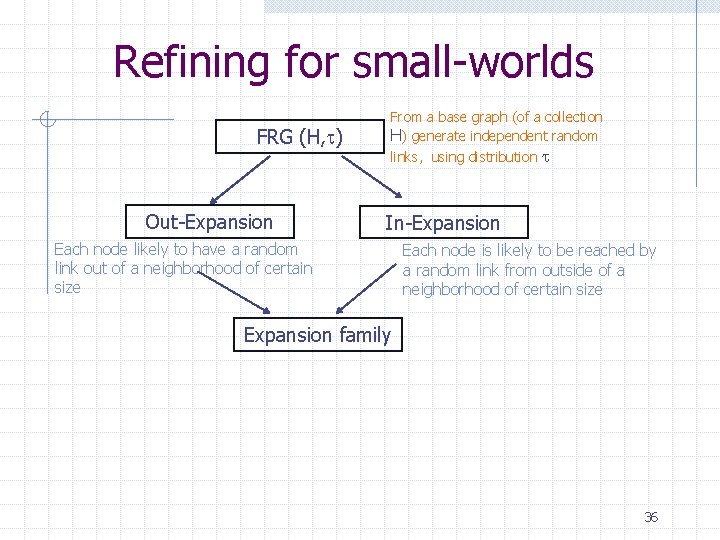
Building Small-World Graphs We start with a general framework where random arcs are added to a fixed base graph. Then we refine this setting additional properties. Create Families of Random Graphs - FRG (H, ): n H: set of base graphs (e. g. grids) n : a distribution for adding random links 29

Building Small World Graphs Based on a random assignment operation: n n n For a given node u, make a random trial under distribution to find another node v Each assignment performs an independent trial E. g. in Kleinberg’s grid setting, w Base graphs are grids d-r (u, v) We want to characterize distributions so most shortest paths are (logn) w is defined as having u v with probability 30

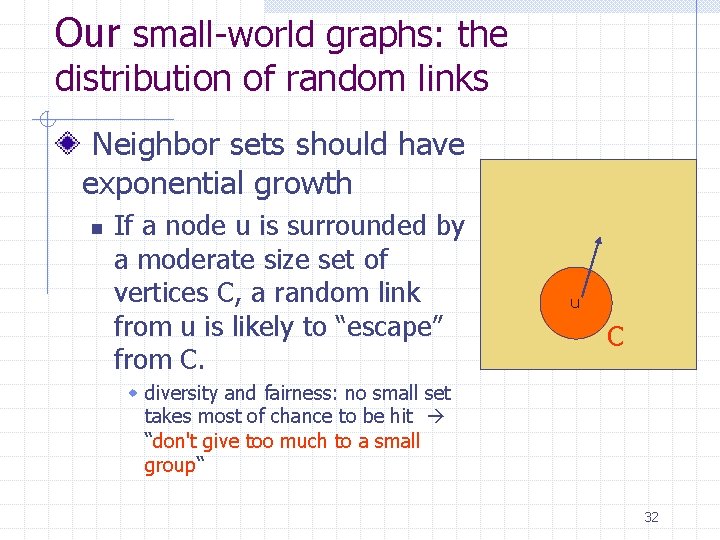
Our small-world graphs: the distribution of random links Neighbor sets should have exponential growth n If a node u is surrounded by a moderate size set of vertices C, a random link from u is likely to “escape” from C. u C 31

Our small-world graphs: the distribution of random links Neighbor sets should have exponential growth n If a node u is surrounded by a moderate size set of vertices C, a random link from u is likely to “escape” from C. u C w diversity and fairness: no small set takes most of chance to be hit “don't give too much to a small group“ 32

Our small-world graphs: the distribution of random links Neighbor sets should have exponential growth n If a node u is surrounded by a moderate size set of vertices C, a random link from u is likely to “escape” from C. u C w We define (in paper) precisely the two parameters: the size of set C and the probability (for escaping from C) 33

Our small-world graphs: the distribution of random links Similar criterion for the `inverse direction’ n If a node u is surrounded by a moderate size set of vertices C, there likely exists a random link coming to u from outside of C. u C 34

Expansion families A Random Family (H, ) is an Expansion Family if the distribution satisfies the two expansion criteria. 35

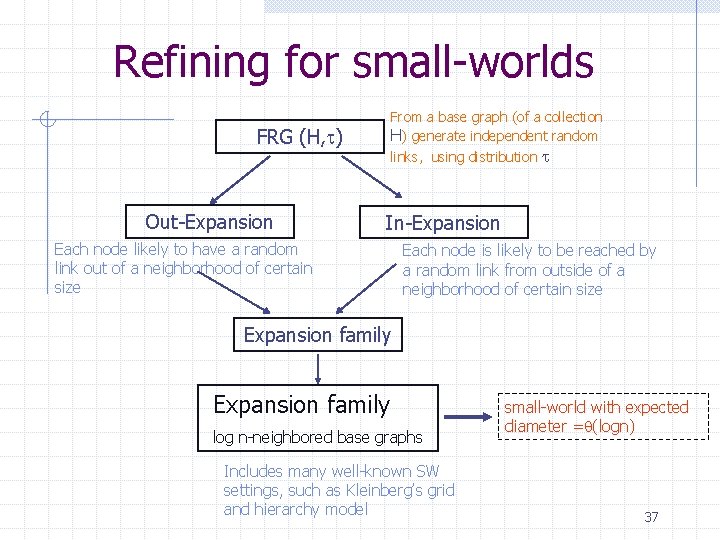
Refining for small-worlds FRG (H, ) Out-Expansion From a base graph (of a collection H) generate independent random links, using distribution In-Expansion Each node likely to have a random link out of a neighborhood of certain size Each node is likely to be reached by a random link from outside of a neighborhood of certain size Expansion family 36

Refining for small-worlds From a base graph (of a collection H) generate independent random FRG (H, ) Out-Expansion links, using distribution In-Expansion Each node likely to have a random link out of a neighborhood of certain size Each node is likely to be reached by a random link from outside of a neighborhood of certain size Expansion family log n-neighbored base graphs Includes many well-known SW settings, such as Kleinberg’s grid and hierarchy model small-world with expected diameter = (logn) 37

Applications of the framework To obtain diameter bounds for some small -world models, n E. g. Kleinberg’s k-dimension grid model for any k 1 (as in our earlier PODC’ 04 paper ) To augment certain settings to become graphs with small diameters n Example is next on Kleinberg’s Tree-based setting Also more: show later 38

Kleinberg’s Tree-based setting Quite different to grid setting n n Nodes are leaves of a full b-ary tree T A distance measure: h(u, v) – the height of the least common ancestor of u and v w That tree T is only used for defining this distance n A random link from a node u can go to v with probability b-h(u, v). No local links possibly unconnected 39

Kleinberg’s Tree-based setting Quite different to grid setting n n n Nodes are leaves of a full b-ary tree T A distance measure: h(u, v) – the height of the least common ancestor of u and v A random link from a node u can go to v with probability b-h(u, v). No local links possibly unconnected If there is at least 3 random links going out from each node, this setting is an Expansion Family n If we add in local links to make an appropriate base graph, then the graph becomes a small-world: w A way to do so, say, ring the nodes within a sub-tree of size logn 40

More refined classes using distance measures We add a general distance function d: V 2 R+ and hence, define our base graphs as growth restricted graphs, where the growth of a neighborhood (nodes within distance r from u) is (r ). n E. g. think of a -D grid but can be any positive real value 41

A phase transition on diameter Class Inv. Dist( , ): We also add random links such that Pr[u v] ~ d- (u, v) E. g. Kleinberg’s 2 -D setting for greedyrouting is Inv. Dist(2, 2) The diameter is poly-log(n) if <2 , but changes to polynomial (n) for >2 42

A Design for Greedy-like Routing We further refining, adding = and some condition on the connectivity of small neighborhoods to gain a class of random graphs where Greedy-like Routing is possible: n n Each node doesn’t have the global topology, but `knows’ a small neighborhood (i. e. knows the random links coming from there) Choose the random link which goes closest to the destination All Kleinberg’s settings (grid, tree, group-induced) are (or after some easy augment) of this class 43

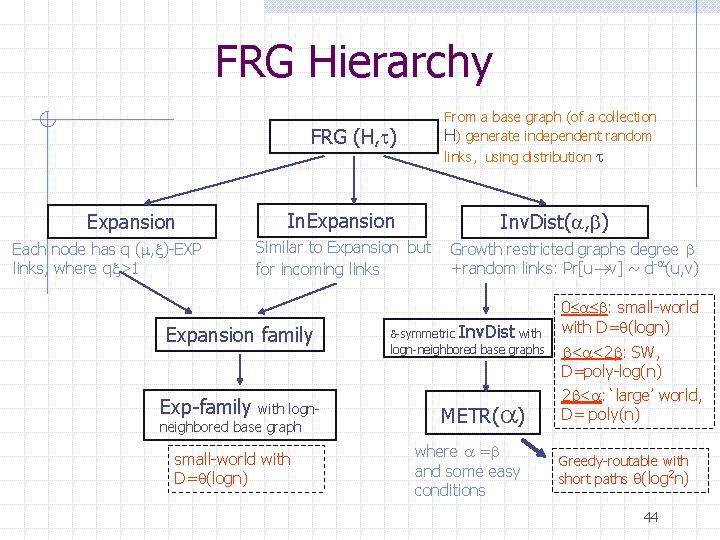
FRG Hierarchy From a base graph (of a collection H) generate independent random FRG (H, ) Expansion Each node has q ( , )-EXP links, where q >1 links, using distribution In. Expansion Inv. Dist( , ) Similar to Expansion but for incoming links Expansion family Exp-family with lognneighbored base graph small-world with D= (logn) Growth restricted graphs degree +random links: Pr[u v] ~ d- (u, v) -symmetric Inv. Dist with logn-neighbored base graphs METR( ) where = and some easy conditions 0 : small-world with D= (logn) < <2 : SW, D=poly-log(n) 2 < : `large’ world, D= poly(n) Greedy-routable with short paths (log 2 n) 44

Future Work Many known Network graphs follow some `growth restricted’ rules. n n E. g. wireless networks can be modeled using the unit disk graph ( =2) The Internet network distance defined by round-trip propagation and transmission delay forms growth restricted metrics (Ng&Zhang, SPAA’ 02) Idea: Using our framework, consider adding long links to certain Network graphs to shrink these graphs (into small-worlds, ideally) n E. g. , how to add in long links (fixed long wire) to a wireless network (unit disk) to best shrink the graph diameter 45