Analyzing an Algorithm Computing the Order of Magnitude

Analyzing an Algorithm Computing the Order of Magnitude Big O Notation

Measuring the Performance of an Algorithm • Order of magnitude describes the growth/running time of an algorithmic process. Example: As the size of the array gets larger, what is the increase in processing time? What happens when we double the data? • The running time of an algorithm is the number of primitive operations executed. • Big-O notation is used to describe the worst-case scenario of an algorithm.

Computing the runtime of an algorithm • It's hard to compute the exact runtime of an algorithm. Runtime depends on: a) The speed of the processor b) Additional tasks being performed and executed in the background. • Instead of talking about the runtime directly, we use big O notation to show quickly the runtime grows.

Measuring how quickly runtime grows • It is only possible to use units of time, such as seconds, when the runtime is measured directly. • Algorithms are measured by how quickly the runtime grows, not speed time. • Order of magnitude uses the size of the data. • Data can become arbitrarily large. • An algorithm may seem inefficient when the data size is small but becomes more efficient when the data size increases. • Big O notation examines the worst case scenario.

Example: What is the runtime of this algorithm? int sum = 0; int k = 0; while (k < n){ sum += a[k]; k++; } Task 1: Determine the number of operations processed by this algorithm.

Counting the operations in an algorithm int sum = 0; int k = 0; while (k < n){ sum += a[k]; k++; } Initialization: 2 operations Loop Statement: n + 1 iterations of two operations 2 + 2 * (n + 1)

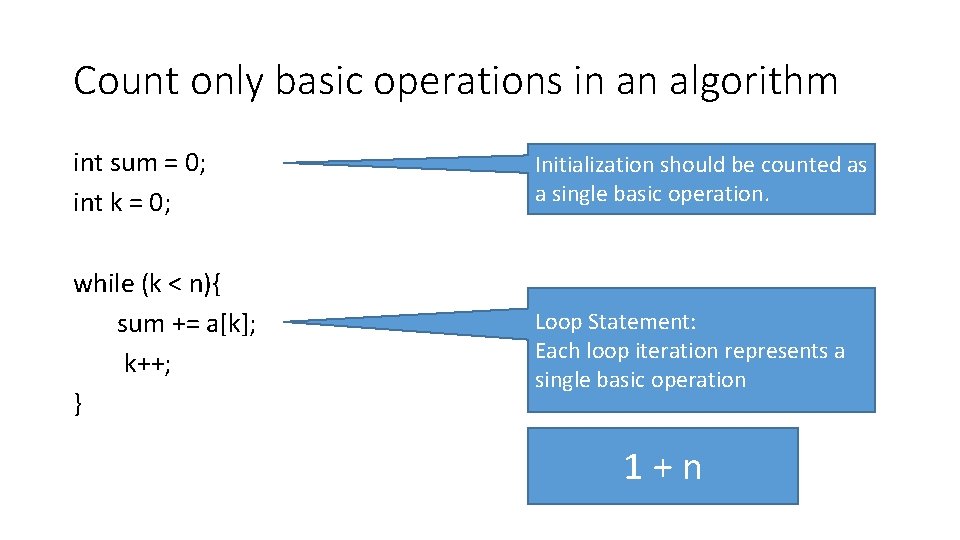
Count only basic operations in an algorithm int sum = 0; int k = 0; Initialization should be counted as a single basic operation. while (k < n){ sum += a[k]; k++; } Loop Statement: Each loop iteration represents a single basic operation 1+n

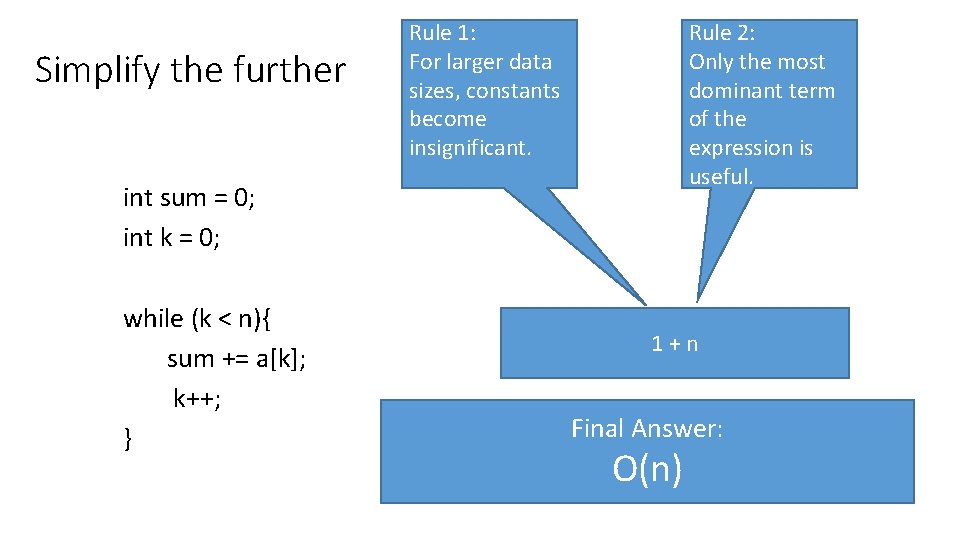
Simplify the further Rule 1: For larger data sizes, constants become insignificant. Rule 2: Only the most dominant term of the expression is useful. int sum = 0; int k = 0; while (k < n){ sum += a[k]; k++; } 1+n Final Answer: O(n)

Practice : Examine the efficiency expression of an algorithm. Determine the Big O notation: a) 1000 n b) 8 n log 2 n + 14 n c) n 3 – n 2 – 3 d) 4 n 2 + 7 n + 2 e) 3 log 2 n + 1 Ans : O(n) O(n log 2 n) ? ? ?

Answers to Practice Problems : Examine the efficiency expression of an algorithm. Determine the Big O notation: a) 1000 n b) 8 n log 2 n + 14 n c) n 3 – n 2 – 3 d) 4 n 2 + 7 n + 2 e) 3 log 2 n + 1 O(n) O(n log 2 n) O (n 3) O(n 2) O(log 2 n)

Searching Efficiency for a Linear Search • Describe the worst case scenario when asked to perform a linear search. How many comparisons are required? • How many comparisons are required for performing a linear search in an average situation? • What is the order of magnitude of efficiency for both the worst and the average case for the linear search?

Searching Efficiency for a Binary Search • Describe the worst case scenario when asked to perform a binary search. • How many comparisons are required? How many comparisons are required for performing a binary search in an average situation? • What is the order of magnitude of efficiency for both the worst and the average case for the binary search?