Analyzing Ambiguity of ContextFree Grammars Claus Brabrand Robert

Analyzing Ambiguity of Context-Free Grammars Claus Brabrand Robert Giegerich Anders Møller brabrand(at)itu. dk robert(at)Tech. Fak. Uni-Bielefeld. de amoeller(at)brics. dk IT Uni. of Copenhagen University of Bielefeld, Germany DAIMI, University of Aarhus CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009

Outline n n Introduction (and Motivation) Characterization of Ambiguity n n n (aka. "Vertical-" and "Horizontal-" Ambiguity) Framework (for Analyzing Ambiguity) Regular Approximation (AMN) Assessment (Applications and Examples) Related Work Conclusion CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [3]

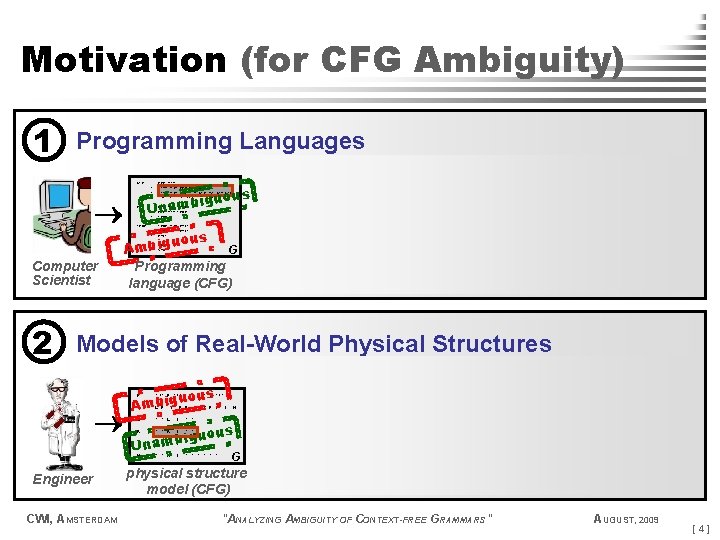
Motivation (for CFG Ambiguity) 1 Programming Languages STM Computer Scientist 2 : | | | EXP "; " "if" "(" EXP ")" STM "else" STM "while" "(" EXP ")" "do" STM : | | EXP "*" TERM EXP "/" TERM : | | TERM "+" FACT TERM "-" FACT : | CONST VAR s biguou Unam EXP uous G Ambig Programming language (CFG) { int f() if (b) if (c) ); f( else y++; } P G parser what the programmer intended P' . . . Models of Real-World Physical Structures Engineer CWI, AMSTERDAM uous Ambig P : "(" P ")" O : L P L : ". " L | | "(" O ")" P R | | S P S ". " | H ous igu Unamb R : ". " R | ". " S : ". " S | ". " H : ". " H | ". " G physical structure model (CFG) M beneficial. . . M' lethal. . . G parser prediction of physical structure ACGAT… "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [4]

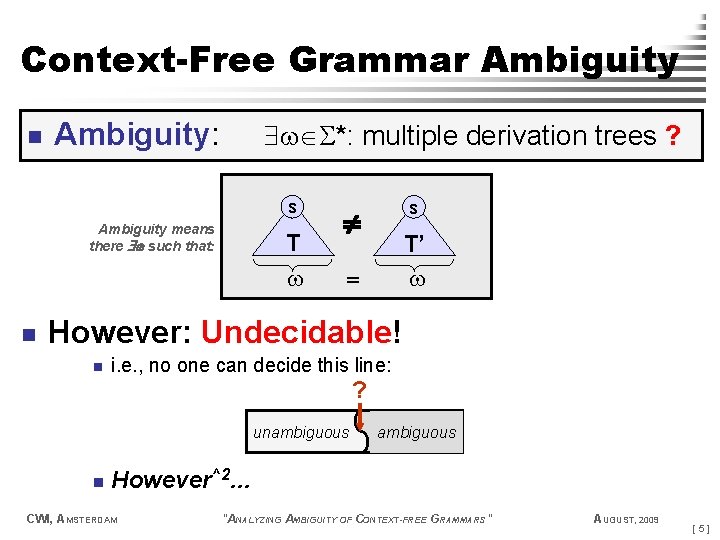
Context-Free Grammar Ambiguity n Ambiguity: *: multiple derivation trees ? s Ambiguity means there such that: n T s T’ = However: Undecidable! n i. e. , no one can decide this line: ? unambiguous n ambiguous However^2… CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [5]

However: Conservative Analysis!. . . just because it’s undecidable, doesn’t mean there aren’t (good) conservative approximations! Indeed, the whole area of static analysis works on “side-stepping undecidability”. n Use conservative (over-)approximation: . unambiguous G Yes! n “Yes!” “G guaranteed unambiguous!” n Safely use any GLR parser on G. . . and never get two parses at runtime! CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [6]

Conservative Analysis (cont'd) n Undecidability means: “there’ll always be a slack”: unambiguous n However, still useful! n . . ambiguous Don't know? Possible interpretations of “Don't know? ”: n n CWI, AMSTERDAM Treat as error (reject grammar): n “Please redesign your grammar” (as in LR(k)) Treat as warning: n “Here are some potential problems” "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [7]

Problems with Existing Solutions 1 Hard to reason (locally) about ambiguity: n Intricate overall structural property of a grammar 2 Are "left-to-right" (or "right-to-left") biased: n Cannot handle "palindromic grammars" (. . . a serious problem for RNA analysis)! 3 Error messages: conflicts: 25 shift/reduce, 13 reduce/reduce Hard to "pin-point ambiguity" (in terms of grammar) n Also: would like "shortest examples" for debugging (. . . especially for grammar non-experts)! n CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [8]

Outline n n Introduction (and Motivation) Characterization of Ambiguity n n n (aka. "Vertical-" and "Horizontal-" Ambiguity) Framework (for Analyzing Ambiguity) Regular Approximation (AMN) Assessment (Applications and Examples) Related Work Conclusion CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [9]

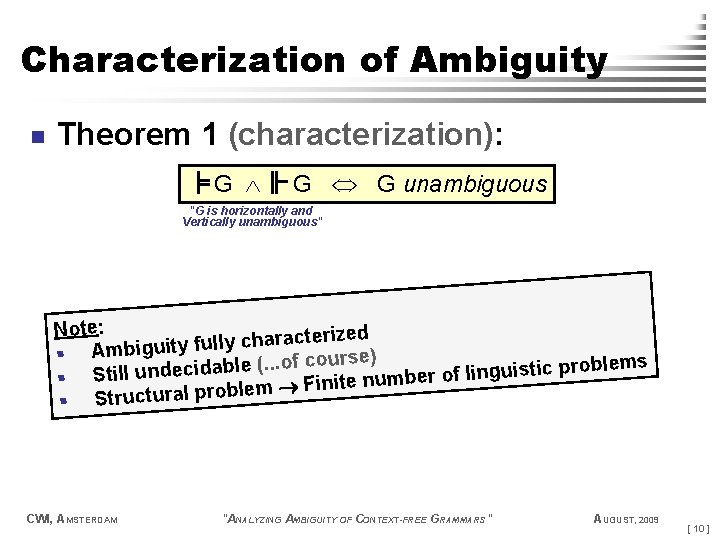
Characterization of Ambiguity n Theorem 1 (characterization): G G G unambiguous "G is horizontally and Vertically unambiguous" Note: rized te c a r a h c y ll fu § Ambiguity ourse) c f o. . (. le b problems a c id ti c e is d u n g u n li ll f ti o S r e § inite numb F m le b o r p l § Structura CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 10 ]

Terminology: Context-Free Grammar EXP : | | ID EXP '+' EXP '*' EXP N N G = N, , s, n n N s N : N P(E*) finite set of nonterminals finite set of terminals start nonterminal production function, E=N Assume (trivially): n n Reachability (all n N reachable from s) Productivity (all n N derive some string) L : E* P( *) CWI, AMSTERDAM "language-of" operator, L(s) "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 11 ]

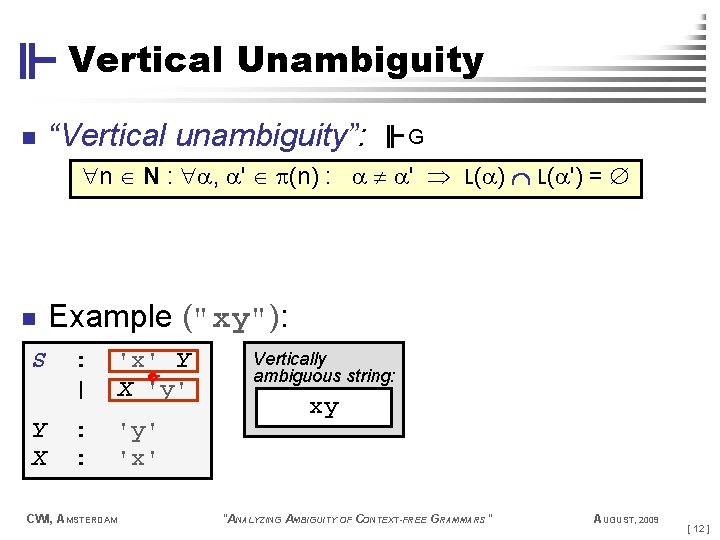
Vertical Unambiguity n “Vertical unambiguity”: G n N : , ' (n) : ' L( ) L( ') = S Y X Example ("xy"): : | 'x' Y X 'y' : : 'y' 'x' n CWI, AMSTERDAM Vertically ambiguous string: xy "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 12 ]

Horizontal Unambiguity n “Horizontal unambiguity”: G L( r) = n N: (n): = l r L( l) : P( *) is given by: where: "overlap" X Y : = { xay | x, y * a + x, xa L(X) y, ay L(Y) } n X Example ("xay"): x S : X Y Horizontallly ambiguous string: V : | 'x' 'a' 'y' xay Y CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" X Y a y Y AUGUST, 2009 [ 13 ]

Characterization of Ambiguity n Theorem 1 (characterization): G G G unambiguous "G is horizontally and Vertically unambiguous" n Lemma 1 a: (“ ”) G n CWI, AMSTERDAM G G unambiguous Lemma 1 b: (“ ”) G (aka. "soundness") (aka. "completeness") G G unambiguous "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 14 ]

Outline n n Introduction (and Motivation) Characterization of Ambiguity n n n (aka. "Vertical-" and "Horizontal-" Ambiguity) Framework (for Analyzing Ambiguity) Regular Approximation (AMN) Assessment (Applications and Examples) Related Work Conclusion CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 15 ]

(Over-)Approximation (A ) n n (Over-)Approximation, A L : E* P( *) E* : L( ) A( ) A : E* P( *) Approximated vertical unambiguity: AG n N : , ' (n) : ' A( ) A( ') = n Approximated horizontal unambiguity: A G A( r) = n N: (n) : = l r A( l) n ” decidable A decidable emptiness of “ ” and “ (on co-dom(A )) CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 16 ]

Unambiguity Approximation n Proposition 2 (approximation soundness): AG n Proof: AG n AG G unambiguous A G G G and hence by transitivity via (Theorem 1) "Larger sets don't overlap smaller sets don't overlap" (contrapositively: "Smaller sets conflict Larger sets conflict"): A( ) A( ') = L( ) L( ') = L( r) = A( r) = L( l) A( l) CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 17 ]

Compositionality (of A's) n Proposition 3 (compositionality): A, A’ decidable (over-)approximations A A’ decidable (over-)approximation n Proof: n Follows from definition [proof omitted] A unambiguous A A’ ambiguous unambiguous A’ n Also: “approximations are locally(!) compositional” CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 18 ]

Are there any Approximations!? ! n Are there any approximations? !? n YES!; e. g. , "The worst. . . approximation" but safe(!) n A *( ) : = * everything (constant) unambiguous worst approximation n Almost useless: n CWI, AMSTERDAM “Can only acquit totally trivial grammars: as unambiguous” "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" N : 'x' AUGUST, 2009 [ 19 ]

Outline n n Introduction (and Motivation) Characterization of Ambiguity n n n (aka. "Vertical-" and "Horizontal-" Ambiguity) Framework (for Analyzing Ambiguity) Regular Approximation (AMN) Assessment (Applications and Examples) Related Work Conclusion CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 20 ]

Regular Approximation (AMN)! n AMN( ) = [Mohri-Nederhof]G( ) n CFG REGDFA (Over-)Approximation “Regular Approximation of Context-Free Grammars through Transformation” [Mohri-Nederhof, 2000] n Properties of this “ Black-box ”: Good (over-)approximation! n Produces regular languages: n n n almost everything is decidable (constructively, via automata)! Note: n Works on a language-level, L(G), . . . n . . . not on the structure-level of the grammar, G CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 21 ]

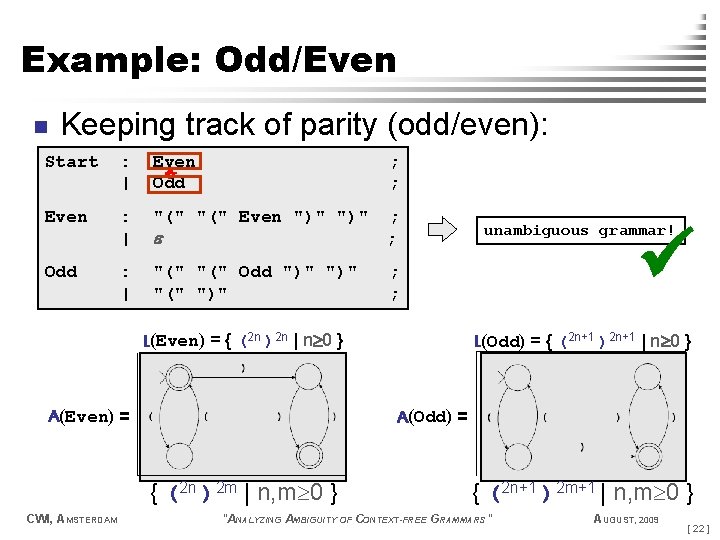
Example: Odd/Even n Keeping track of parity (odd/even): : | Even Odd ; ; Even : | "(" Even ")" ; ; Odd : | "(" Odd ")" "(" ")" ; ; Start L(Even) = { (2 n )2 n | n 0 } A(Even) = L(Odd) = { (2 n+1 )2 n+1 | n 0 } A(Odd) = { (2 n )2 m | n, m 0 } CWI, AMSTERDAM unambiguous grammar! { (2 n+1 )2 m+1 | n, m 0 } "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 22 ]

Outline n n Introduction (and Motivation) Characterization of Ambiguity n n n (aka. "Vertical-" and "Horizontal-" Ambiguity) Framework (for Analyzing Ambiguity) Regular Approximation (AMN) Assessment (Applications and Examples) Related Work Conclusion CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 23 ]

Assessment (implementation) n Java implementation: n 7, 400 lines of code (command line + GU interface) [ www. brics. dk/grammar/ ] CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 24 ]

Technology Transfer n Integrated in Dot. Vocal's "Grammar Studio": Ambiguity analysis: Grammar Studio provides developers a powerful algorithm to test the vertical and horizontal ambiguities. Erasing any ambiguity in a grammar means to improve the effectiveness and by consequence the recognition too. CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 25 ]

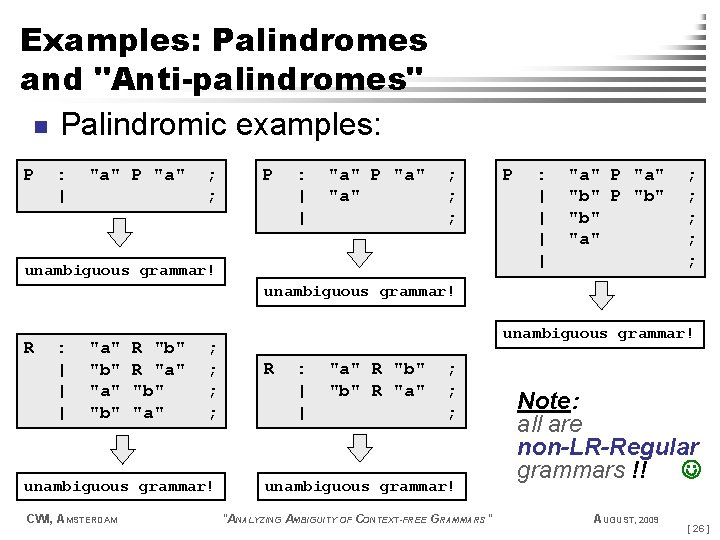
Examples: Palindromes and "Anti-palindromes" n Palindromic examples: P : | "a" P "a" ; ; P : | | "a" P "a" ; ; ; unambiguous grammar! P : | | "a" P "a" "b" P "b" "a" ; ; ; unambiguous grammar! R : | | | "a" "b" R "a" "b" "a" ; ; unambiguous grammar! CWI, AMSTERDAM unambiguous grammar! R : | | "a" R "b" R "a" ; ; ; unambiguous grammar! "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" Note: all are non-LR-Regular grammars !! AUGUST, 2009 [ 26 ]

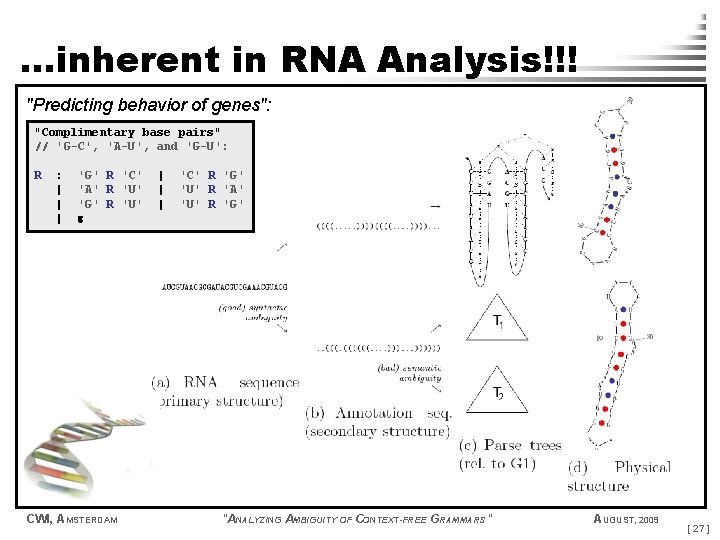
. . . inherent in RNA Analysis!!! "Predicting behavior of genes": "Complimentary base pairs" // 'G-C', 'A-U', and 'G-U': R : | | | 'G' R 'C' 'A' R 'U' 'G' R 'U' CWI, AMSTERDAM | | | 'C' R 'G' 'U' R 'A' 'U' R 'G' "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 27 ]

Examples: RNA Analysis (G 1) n RNA Analysis (G 1): %> java –jar Grambiguity. jar G 1. cfg *** vertical ambiguity detected: 'S[a. S]' vs. 'S[Sa]' ambiguous string: ". " *** vertical ambiguity detected: 'S[aa]' vs. 'S[SS]' ambiguous string: "()" *** vertical ambiguity detected: 'S[a. S]' vs. 'S[SS]' ambiguous string: ". " /* ambiguous */ G 1 S[aa] [a. S] [Sa] [SS] [empty] : | | "(" S ")" ; ". " S ; S ". " ; S S ; ; *** vertical ambiguity detected: 'S[Sa]' vs. 'S[SS]' ambiguous string: ". " *** vertical ambiguity detected: 'S[SS]' vs. 'S[empty]' ambiguous string: "" *** horizontal ambiguity detected: 'S[SS: 0. . 0]' vs. 'S[SS: 1. . 1]' ambiguous string: ". " *** ambiguous grammar: 5 vertical ambiguities 1 horizontal ambiguity CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 28 ]

Examples: RNA Analysis (G 2) n RNA Analysis (G 2): *** vertical ambiguity detected: 'S[a. S]' vs. 'S[Sa]' ambiguous string: ". " *** vertical ambiguity detected: 'S[a. Pa]' vs. 'S[SS]' ambiguous string: "()" *** vertical ambiguity detected: 'S[a. S]' vs. 'S[SS]' ambiguous string: ". " *** vertical ambiguity detected: 'S[Sa]' vs. 'S[SS]' ambiguous string: ". " /* ambiguous */ G 2 S[a. Pa] [a. S] [Sa] [SS] [empty] : | | "(" P ")" ; ". " S ; S ". " ; S S ; ; P[a. Pa] [S] : "(" P ")" ; | S ; *** vertical ambiguity detected: 'S[SS]' vs. 'S[empty]' ambiguous string: "" *** vertical ambiguity detected: 'P[a. Pa]' vs. 'P[S]' ambiguous string: "()" *** horizontal ambiguity detected: 'S[SS: 0. . 0]' vs. 'S[SS: 1. . 1]' ambiguous string: ". " *** ambiguous grammar: 6 vertical ambiguities 1 horizontal ambiguity CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 29 ]

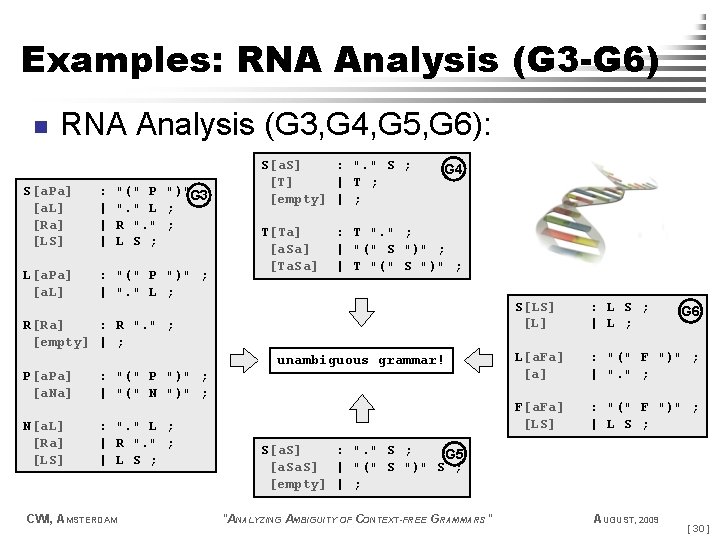
Examples: RNA Analysis (G 7+G 8) RNA Analysis (G 7, G 8): *** (potential) vertical ambiguity detected: 'P[a. Pa]' vs. 'P[a. Na]' shortest ambiguous string: "(((. )" S[a. Pa] [a. L] [Ra] [LS] : | | | *** (potentially) ambiguous grammar: 1 (potential) vertical ambiguity 0 (potential) horizontal ambiguities L[a. Pa] [a. L] : "(" P ")" ; | ". " L ; n S[a. S] : ". " S ; [T] | T ; [empty] | ; G 8 T[Ta] : T ". " ; [a. Pa] | "(" P ")" ; [Ta. Pa] | T "(" P ")" ; P[a. Pa] [a. Na] : "(" P ")" ; | "(" N ")" ; Note: these are all spurious errors due to imprecisions in the analysis Acquitted as unambiguous using unfolding technique! "(" P ")" G 7 ; ". " L ; R ". " ; L S ; R[Ra] : R ". " [empty] | ; ; P[a. Pa] [a. Na] : "(" P ")" ; | "(" N ")" ; N[a. L] [Ra] [LS] : ". " L | R ". " | L S ; ; ; *** (potential) vertical ambiguity detected: 'P[a. Pa]' vs. 'P[a. Na]' shortest ambiguous string: "(((. )" N[a. S] : ". " S ; *** (potentially) ambiguous grammar: [Ta] | T ". " ; 1 (potential) vertical ambiguity [Ta. Pa] | T "(" P ")" ; 0 (potential) horizontal ambiguities CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 31 ]

Examples: "voss" & "voss-light" P : "(" P ")" ; | "(" O ")" ; O : | | | L P ; P R ; S P S ; H ; // P: Closed structure // O: Open structure L : ". " L ; | ". " ; // L: Left bulge R : ". " R ; | ". " ; // R: Right bulge S : ". " S ; | ". " ; // S: Singlestrand H : ". " H ; | ". " ; // H: Hairpin 3+loop CWI, AMSTERDAM LR(k): LR(1) LR(3) LR(5) LR(7) LR(9). . . = 3 r/r = 12 r/r = 93 r/r = 249 r/r = 513 r/r conflicts conflicts unambiguous grammar! "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 32 ]

Example: Java Expressions Exp[assign] [exp 1] : | Exp 1 "=" Exp 1 ; ; Exp 1[or] [exp 2] : | Exp 1 "||" Exp 2 ; ; Exp 2[and] [exp 3] : | Exp 2 "&&" Exp 3 ; ; Exp 3[eq] [neq] [exp 4] : | | Exp 3 "==" Exp 4 Exp 3 "!=" Exp 4 ; ; ; Exp 4[lt] [leq] [gt] [geq] [exp 5] : | | Exp 4 Exp 5 ; ; ; "<" Exp 5 "<=" Exp 5 ">=" Exp 5 /* -- cont'd -- */ Exp 5[add] [sub] [exp 6] : | | Exp 5 "+" Exp 6 Exp 5 "-" Exp 6 ; ; ; Exp 6[mul] [div] [exp 7] : | | Exp 6 "*" Exp 7 Exp 6 "/" Exp 7 ; ; ; Exp 7[not] [exp 8] : | "!" Exp 7 Exp 8 ; ; Exp 8[par] [con] : | "(" Exp ")" Con ; ; Con[num] [id] : | "0" "x" ; ; unambiguous grammar! CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 33 ]

Error Messages (Amb. Example) Ambiguous Expressions: E[plus] [mult] [x] : | | E "+" E E "*" E "x" n ; ; ; *** vertical ambiguity detected: 'E[plus]' vs. 'E[mult]' ambiguous string: ”x*x+x” *** horizontal ambiguity detected: 'E[plus: 0. . 0]' vs. 'E[plus: 1. . 2]' ambiguous string: ”x+x+x” *** horizontal ambiguity detected: 'E[plus: 0. . 1]' vs. 'E[plus: 2. . 2]' ambiguous string: ”x+x+x” *** horizontal ambiguity detected: 'E[mult: 0. . 0]' vs. 'E[mult: 1. . 2]' ambiguous string: ”x*x*x” *** horizontal ambiguity detected: 'E[mult: 0. . 1]' vs. 'E[mult: 2. . 2]' ambiguous string: ”x*x*x” precedence "+" vs. "*" assoc. of "+" assoc. of "*" *** ambiguous grammar: 1 vertical ambiguity 4 horizontal ambiguities CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 34 ]

Benchmark Grammars UNAMBIGUOUS . . LR(k) LR(8) LR(7) LR(6) LR(5) LR(4) LR(3) LR(2) LR(1) LALR(1) G 8 Exp O/E G 6 G 1 (5 V+1 H) Amb-Exp (1 V+4 H) G 4 G 5 G 2 (6 V+1 H) P Base Voss R G 3 G 7 Voss-light [OUR] AMBIGUOUS CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 35 ]

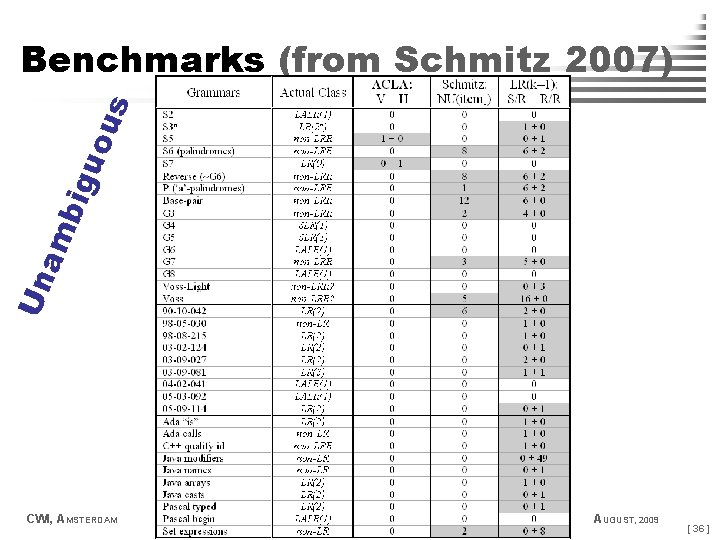
Un am b igu ou s Benchmarks (from Schmitz 2007) CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 36 ]

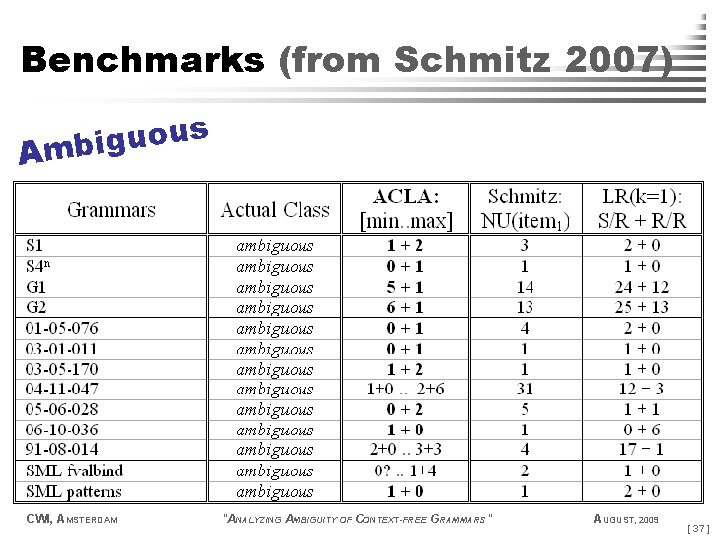
Benchmarks (from Schmitz 2007) s u o u g i Amb CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 37 ]

Outline n n Introduction (and Motivation) Characterization of Ambiguity n n n (aka. "Vertical-" and "Horizontal-" Ambiguity) Framework (for Analyzing Ambiguity) Regular Approximation (AMN) Assessment (Applications and Examples) Related Work Conclusion CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 38 ]

Related Work (Dynamic) n Dynamic disambiguation: n “Disambiguation-by-convention”: n n Customizable: n n n Longest match, most specific match, … [Bison v. 1. 5+]: %dprec, %merge [ASF+SDF]: “disambiguation filters” Dynamic ambiguity interception: GLR ([Tomita], [Early], [Bison], [ASF+SDF], …) n [AMBER] n CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 39 ]

Related Work (Static) n Static disambiguation: n “Disambiguation-by-convention”: n n Customizable: n n First match, most specific match, … [Yacc]: %left, %right, %nonassoc, %prec Static ambiguity interception: n n n Our work goes here LL(k), LALR(1), LR(k), LR-regular, … Sylvain Schmitz (ICALP 2007): : A A S "Conservative Ambiguity Detection in Context-Free Grammars" : 'a' A 'a' "An Experimental Ambiguity Detection Tool" (LDTA A 2007) n Subsumes LR-regular, Incomparable to our technique | 'b' CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 40 ]

Comparative Related Work n "Ambiguity Detection Methods for Context-Free Grammars" H. J. S. Basten (Master's thesis) n CWI, Universiteit van Amsterdam, Holland n n "Ambiguity Detection for Context-Free Grammars in Eli" Michael Kruse (Master's thesis) n Uni. Paderborn, Germany n CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 41 ]

Outline n n Introduction (and Motivation) Characterization of Ambiguity n n n (aka. "Vertical-" and "Horizontal-" Ambiguity) Framework (for Analyzing Ambiguity) Regular Approximation (AMN) Assessment (Applications and Examples) Related Work Conclusion CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 42 ]

Conclusion n Advantages (of our approach): Characterization! n Possible to reason (locally) about ambiguity n (Composable) Analysis Framework n Complete decision procedure for regular grammars n Inherently parallelizable n DFA Counterexamples: n and shortest (possibly) ambiguous string n Not "left-to-right" or "right-to-left" biased: n Can handle palindromic grammars n Well-suited for RNA analysis : ) n CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 43 ]

Conclusion (cont'd) “Analyzing Ambiguity of Context-Free Grammars” It has been known since 1962 that the ambiguity problem for context-free grammars is undecidable. Ambiguity in context-free grammars is a recurring problem in language design and parser generation, as well as in applications where grammars are used as models of real-world physical structures. However, the fact that the problem is undecidable does not mean that there are no useful approximations to the problem. We observe that there is a simple linguistic characterization of the grammar ambiguity problem, and we show to exploit this to conservatively approximate the problem based on local regular approximations and grammar unfoldings. As an application, we consider grammars that occur in RNA analysis in bioinformatics, and we demonstrate that our static analysis of context-free grammars is sufficiently precise and efficient to be practically useful. CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 44 ]

Thank you Questions, please? CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009

BONUS SLIDES CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009

Other Approximation Strategies n The ”Empty. String” Approximation: n The ”May. Must” Approximation: n … CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 47 ]

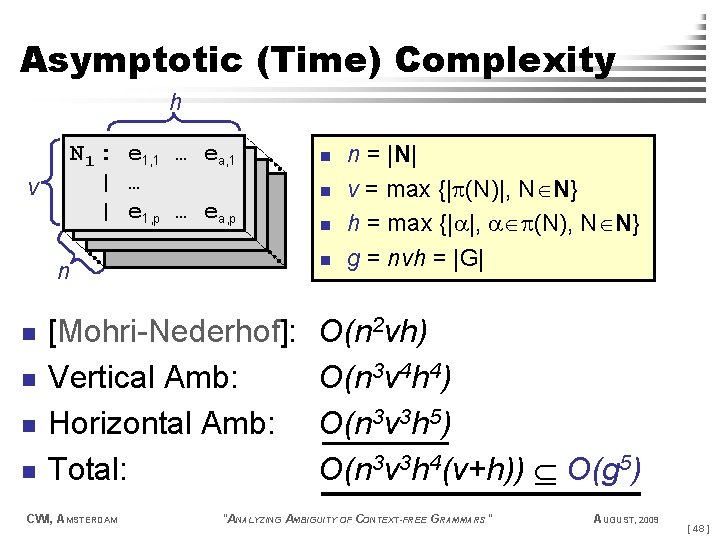
Asymptotic (Time) Complexity h N 1 : e 1, 1 … ea, 1 | … | e 1, p … ea, p v n n n [Mohri-Nederhof]: Vertical Amb: Horizontal Amb: Total: CWI, AMSTERDAM n n n n = |N| v = max {| (N)|, N N} h = max {| |, (N), N N} g = nvh = |G| O(n 2 vh) O(n 3 v 4 h 4) O(n 3 v 3 h 5) O(n 3 v 3 h 4(v+h)) O(g 5) "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 48 ]

AMN is Decidable! n X. Y = n Constructively decidable (using DFAs): n n Y = X n Constructively decidable (using DFAs): n n O(|XDFA||YDFA|) AMN Constructively decidable n with potential counterexamples (as DFAs); i. e. , we can extract shortest (potentially ambiguous) strings! CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 49 ]

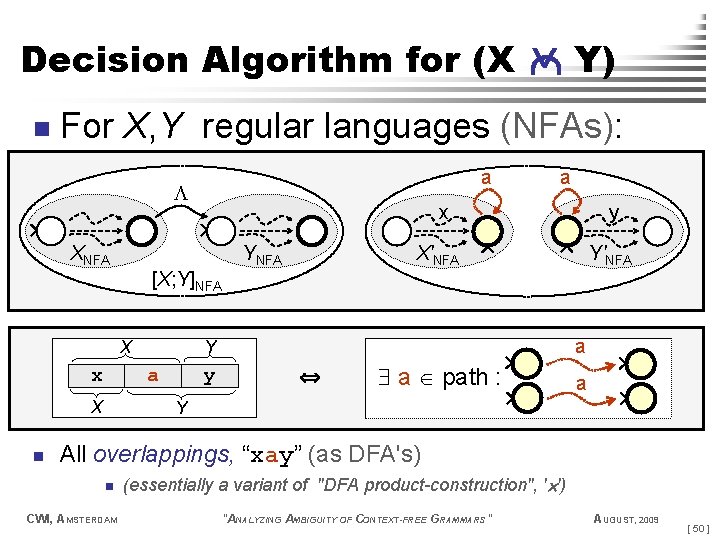
Y) Decision Algorithm for (X n For X, Y regular languages (NFAs): a a x XNFA YNFA y X'NFA Y'NFA [X; Y]NFA X x a X n a Y y a path : a Y All overlappings, “xay” (as DFA's) n CWI, AMSTERDAM (essentially a variant of "DFA product-construction", ' ') "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 50 ]

Example: Expressions n Expressions: E[term] : T [plus] | E "+" T T[x] [par] Note: General problem with non-linear recursive structures ; ; : "x" ; | "(" E ")" ; However, there's a trick. . . *** (potential) vertical ambiguity detected: 'E[term]' vs. 'E[plus]' shortest ambiguous string: "x+x" *** (potential) horizontal ambiguity detected: 'E[plus: 0. . 0]' vs. 'E[plus: 1. . 2]' shortest ambiguous string: "x+x+x" *** (potential) horizontal ambiguity detected: 'E[plus: 0. . 1]' vs. 'E[plus: 2. . 2]' shortest ambiguous string: "x+x+x" *** (potentially) ambiguous grammar: 1 (potential) vertical ambiguity 2 (potential) horizontal ambiguities CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 51 ]

Examples: Expressions (cont'd) Expressions: E[term] : T [plus] | E "+" T T[x] [par] ; ; : "x" ; | "(" E ")" ; T[x] [par] : "x" ; | "(" E ")" ; E[term] : T [plus] | E "+" T T[x] [par] ; ; : "x" ; | "(" E ")" ; CWI, AMSTERDAM E : T : E "+" T E AST = x+(x+(x+x)+x)+x G unfold wrt. '(' and ')' E[term] : T [plus] | E "+" T unfold trick: (inside/outside) parentheses G Gu n Gu T : "x" : "(" E ")" E : T : E "+" T T : "x" : "(" E ")" E ASTu u = x+(x+(x+x)+x)+x E : T : E "+" T T : "x" : "(" E ")" unambiguous grammar! "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 52 ]

Proof (Lemma 1 a): “ ” n Lemma 1 a: G n G G unambiguous …contrapositively: G ambiguous n G G Proof structure: n Assume G ambiguous (i. e. 2 der. trees for ) n Show: n CWI, AMSTERDAM G G by induction in max height of the 2 derivation trees "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 53 ]

Proof (Lemma 1 a): “ ” (Base) n Base case (height 1): n The ambiguity means that: 1 N n = N ’ 1 However, this means that: = t 0 t 1. . t| |-1 = ' (i. e. the two trees must be the same); and so the result holds vacuously CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 54 ]

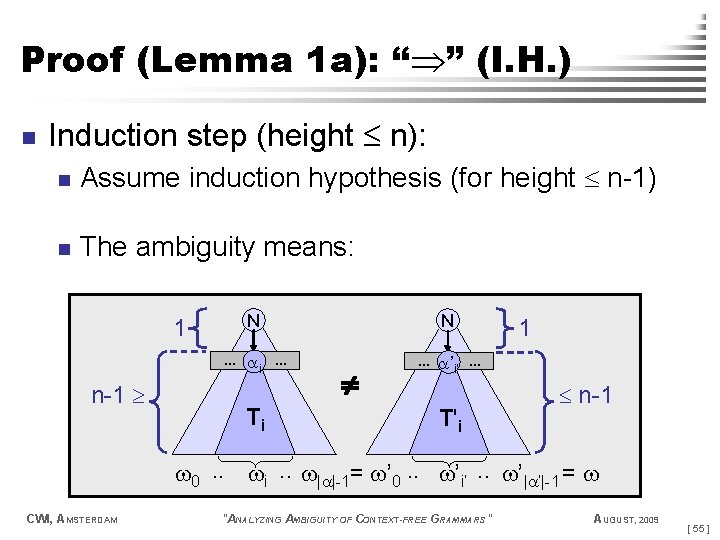
Proof (Lemma 1 a): “ ” (I. H. ) n Induction step (height n): n Assume induction hypothesis (for height n-1) n The ambiguity means: 1 n-1 N N … i … … ’i’ … Ti T'i 1 n-1 0. . i. . | |-1= ’ 0. . ’i’. . ’| ’|-1 = CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 55 ]

Proof (Lemma 1 a): “ ” ( ’) 1 n-1 N N … i … … ’i’ … Ti 1 n-1 T'i 0. . i. . | |-1= ’ 0. . ’i’. . ’| ’|-1 = n Case ’ (i. e. different production): n …but then n CWI, AMSTERDAM L( ) L( ’) { } i. e. , we have a vertical ambiguity: "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" G AUGUST, 2009 [ 56 ]

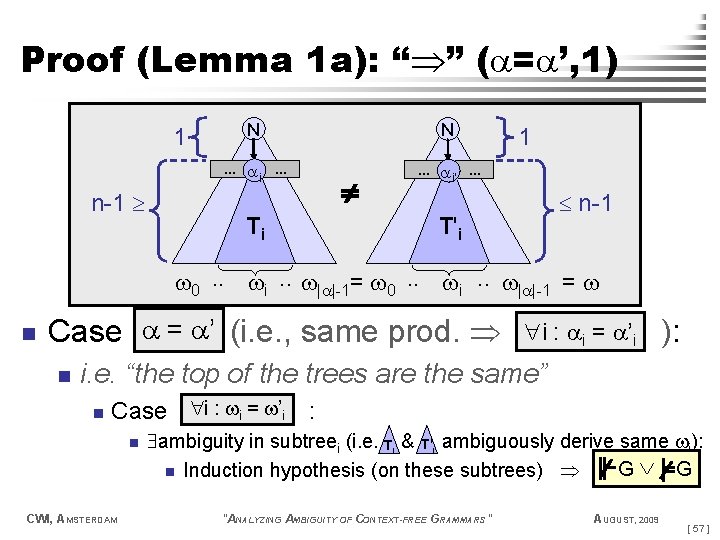
Proof (Lemma 1 a): “ ” ( = ’, 1) 1 n-1 N N … i … … i’ … Ti 1 n-1 T'i 0. . i. . | |-1= 0. . i. . | |-1 = n Case = ’ (i. e. , same prod. n i : i = ’i ): i. e. “the top of the trees are the same” n Case i : i = ’i : n CWI, AMSTERDAM ambiguity in subtreei (i. e. Ti & T'i ambiguously derive same i): G G n Induction hypothesis (on these subtrees) "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 57 ]

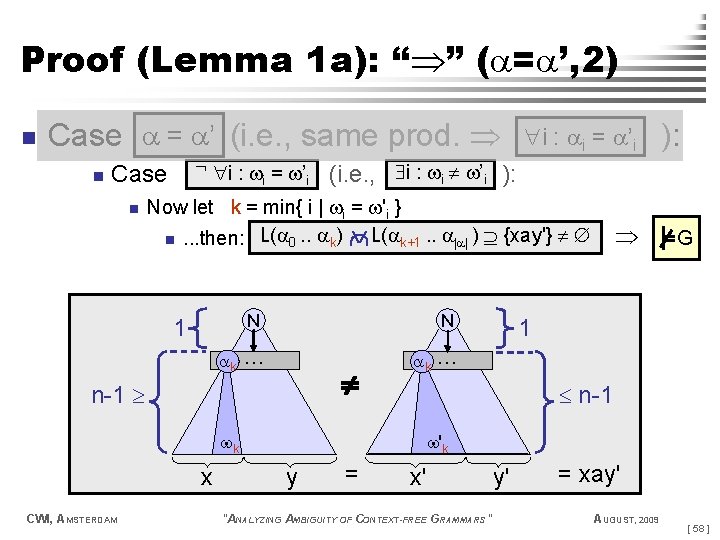
Proof (Lemma 1 a): “ ” ( = ’, 2) n Case = ’ (i. e. , same prod. n i : = ’ i i Case n N k N . . . n-1 k G 1 . . . n-1 'k k x ): (i. e. , i : i ’i ): Now let k = min{ i | i = 'i } L( k+1. . | | ) {xay'} n. . . then: L( 0. . k) 1 CWI, AMSTERDAM i : i = ’i y = x' "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" y' = xay' AUGUST, 2009 [ 58 ]

Proof (Lemma 1 b): “ ” Lemma 1 b: G n G G unambiguous . . . contrapositively: G ambiguous n G G Proof: Assume “ ” (vertical conflict): n N * a, N ’ * a, L( ) L( ’) {a} n But then derive (using reachability + derivability of N): s * x N x * x a y s * x N x ’ * x a y CWI, AMSTERDAM for some N "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" G ambiguous n AUGUST, 2009 [ 59 ]

Proof (Lemma 1 b): “ ” (cont’d) n Assume “ ” (horizontal conflict): n Then for some N N: N l r , where L( l) L( r) i. e. x, y * : a + : x, xa L( l) y, ay L( r) But then derive (using reachability + derivability of N): s * v N v l r * v x r * v x a y w s * v N v l r * v x a y w CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 G ambiguous n [ 60 ]

Vertical & Horizontal Unamb. n Theorem: n “Vertical unambiguity”: G G G unambiguous G n N : , ' (n) : ' L( ) L( ') = n “Horizontal unambiguity”: G L( r) = n N: (n): = l r L( l) : P( *) "overlap" X Y : = { xay | x, y * a + x, xa L(X) y, ay L(Y) } CWI, AMSTERDAM "ANALYZING AMBIGUITY OF CONTEXT-FREE GRAMMARS" AUGUST, 2009 [ 61 ]