Analytick geometria kvadratickch tvarov Rovnica paraboly Defincia paraboly

Analytická geometria kvadratických útvarov Rovnica paraboly

Definícia paraboly Parabola je množina všetkých bodov v rovine, ktoré majú od daného pevného bodu a pevne danej priamky rovnakú vzdialenosť. ukážka v Geogebre

Prvky paraboly • V[m, n] – vrchol • F – ohnisko d – určujúca priamka • DF – os paraboly • FD = p – parameter • FV = DV = p/2

Dôležité vzťahy o zvolíme súradnicovú sústavu tak, aby jej začiatok bol vo vrchole, x-ová os bola os paraboly a y-ová os prechádzala vrcholom paraboly o súradnice význačných bodov budú: V[0, 0] F[p/2, 0] D[-p/2, 0] priamka: 2 x + p = 0 alebo x = - p / 2

Rovnica paraboly Odvodenie • vzdialenosť ľubovoľného bodu X od ohniska a priamky je rovnaká • postupným odvodzovaním dostaneme rovnicu • Tento vzťah nazývame rovnica paraboly

Rovnica paraboly Odvodenie • ak stred bude v ľubovoľnom bode súradnicovej sústavy

Druhy parabol A) os paraboly je rovnobežná s osou x 1. ohnisko je v kladnej časti polosi 2. ohnisko je v zápornej časti polosi • ak stred S[0, 0] • ak stred S[m, n]

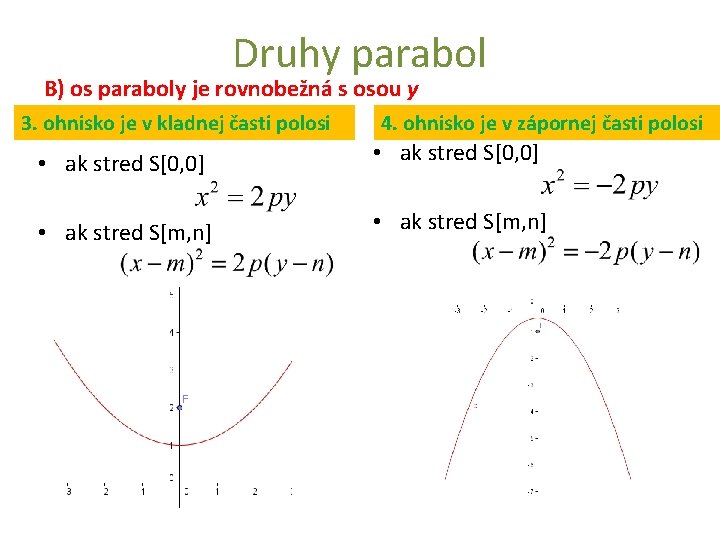
Druhy parabol B) os paraboly je rovnobežná s osou y 3. ohnisko je v kladnej časti polosi 4. ohnisko je v zápornej časti polosi • ak stred S[0, 0] • ak stred S[m, n]

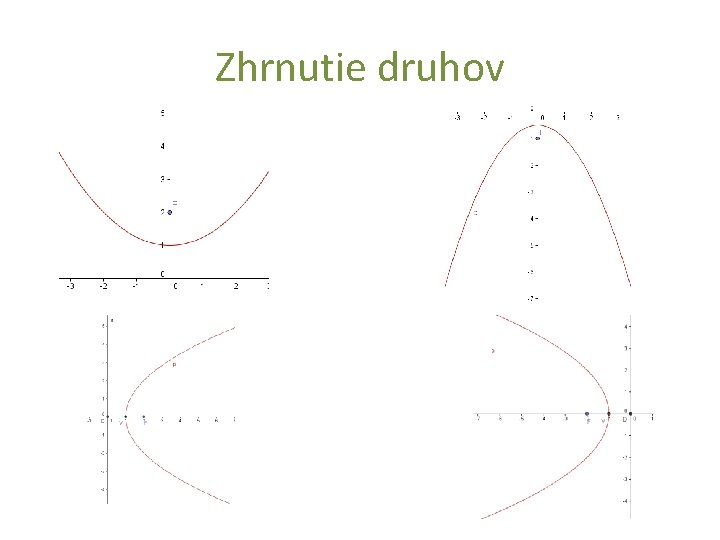
Zhrnutie druhov

Rovnica paraboly – riešené príklady Napíšte rovnicu paraboly, ktorá má vrchol V a ohnisko F. F je vpravo od V (kladná časť osi) rovnobežná s x F je pod od V (záporná časť osi) rovnobežná s y

Rovnica paraboly – riešené príklady Z rovnice paraboly určte súradnice vrcholu, ohniska a parameter.

koniec