Analytick geometria kvadratickch tvarov Osov rovnica hyperboly Defincia

Analytická geometria kvadratických útvarov Osová rovnica hyperboly

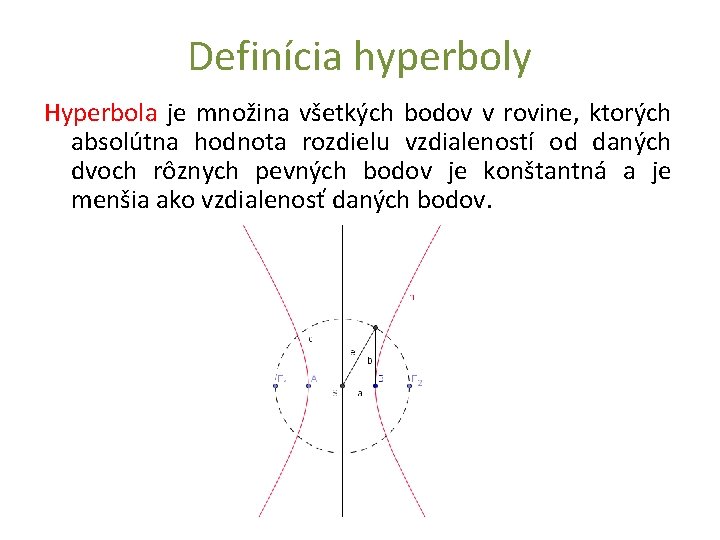
Definícia hyperboly Hyperbola je množina všetkých bodov v rovine, ktorých absolútna hodnota rozdielu vzdialeností od daných dvoch rôznych pevných bodov je konštantná a je menšia ako vzdialenosť daných bodov.

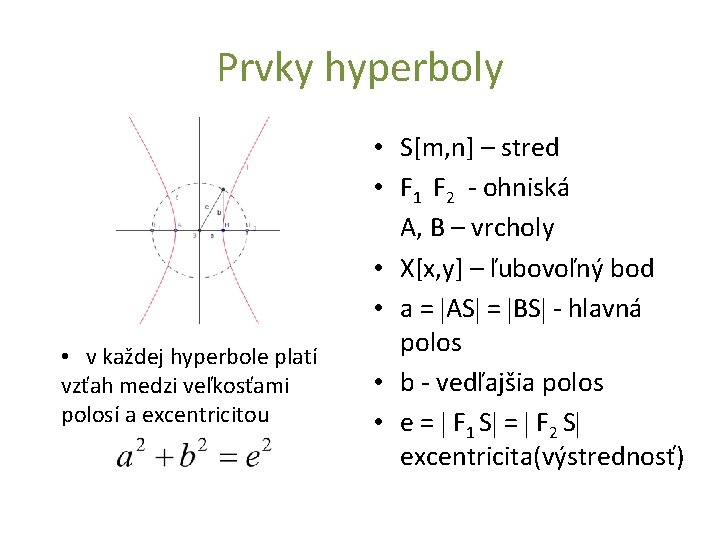
Prvky hyperboly • v každej hyperbole platí vzťah medzi veľkosťami polosí a excentricitou • S[m, n] – stred • F 1 F 2 - ohniská A, B – vrcholy • X[x, y] – ľubovoľný bod • a = AS = BS - hlavná polos • b - vedľajšia polos • e = F 1 S = F 2 S excentricita(výstrednosť)

Dôležité vzťahy o zvolíme súradnicovú sústavu tak, aby jej začiatok bol v strede hyperboly, x-ová os bola hlavná os hyperboly a yová os bola vedľajšia os. o súradnice význačných bodov budú: S[0, 0] F 1[-e, 0], F 2[e, 0], A[-a, 0], B[a, 0],

Osová rovnica hyperboly Odvodenie • rozdiel vzdialeností ľubovoľného bodu X od ohnísk v absolútnej hodnote je 2 a • postupným odvodzovaním dostaneme rovnicu • Tento vzťah nazývame osová rovnica hyperboly

Osová rovnica hyperboly Odvodenie • ak stred bude v ľubovoľnom bode súradnicovej sústavy • Tento vzťah nazývame osová rovnica hyperboly

Osová rovnica hyperboly – riešené príklady Napíšte osovú rovnicu hyperboly, ktorá má stred v bode S a polosi a, b.

Osová rovnica hyperboly – riešené príklady Z osovej rovnice hyperboly určte súradnice stredu a veľkosti polosí hyperboly.

Príklady na precvičenie 1. Napíšte osovú rovnicu hyperboly, ak: a) S[2, -4], a = 8, e = 10 b) S[-1, 2], e = 5, b = 3 riešenie 2. Zistite veľkosť polosí hyperboly a ohniskovú vzdialenosť, ak je hyperbola daná rovnicou: a) b) c) d) e) f) 9 x 2 – 16 y 2 = 144 riešenie x 2 – 4 y 2 = 16 9 x 2 – 36 y 2 = 324 riešenie 4 x 2 – y 2 = 16 riešenie 3(x + 2)2 – (y + 1)2 = 3 25(x – 3)2 – 16(y – 7)2 = 400 riešenie

koniec

Príklad 1 Napíšte osovú rovnicu hyperboly, ak: a) S[2, -4], a = 8, e = 10 b) S[-1, 2], e = 5, b = 3 späť

Príklad 2 a) Zistite veľkosť polosí hyperboly a ohniskovú vzdialenosť, ak je hyperbola daná rovnicou: 9 x 2 – 16 y 2 = 144 späť

Príklad 2 b) Zistite veľkosť polosí hyperboly a ohniskovú vzdialenosť, ak je hyperbola daná rovnicou: x 2 – 4 y 2 = 16 späť

Príklad 2 c) Zistite veľkosť polosí hyperboly a ohniskovú vzdialenosť, ak je hyperbola daná rovnicou: 9 x 2 – 36 y 2 = 324 späť

Príklad 2 d) Zistite veľkosť polosí hyperboly a ohniskovú vzdialenosť, ak je hyperbola daná rovnicou: 4 x 2 – y 2 = 16 späť

Príklad 2 e) Zistite veľkosť polosí hyperboly a ohniskovú vzdialenosť, ak je hyperbola daná rovnicou: 3(x + 2)2 – (y + 1)2 = 3 späť

Príklad 2 f) Zistite veľkosť polosí hyperboly a ohniskovú vzdialenosť, ak je hyperbola daná rovnicou: 25(x – 3)2 – 16(y – 7)2 = 400 späť