Analytick geometria kvadratickch tvarov Osov rovnica elipsy Defincia







![Príklady na precvičenie 1. Napíšte osovú rovnicu elipsy, ak: a) S[2, -4], a = Príklady na precvičenie 1. Napíšte osovú rovnicu elipsy, ak: a) S[2, -4], a =](https://slidetodoc.com/presentation_image/0adeb80c1c0dd114aa69abe45f194557/image-9.jpg)

![Odvodenie 2 S[0, 0] F 1[-e, 0], F 2[e, 0], A[-a, 0], B[a, 0], Odvodenie 2 S[0, 0] F 1[-e, 0], F 2[e, 0], A[-a, 0], B[a, 0],](https://slidetodoc.com/presentation_image/0adeb80c1c0dd114aa69abe45f194557/image-12.jpg)
![Riešenie 3 Napíšte rovnicu elipsy, ktorá prechádza bodmi A[8, 3], B[6, 4] a stred Riešenie 3 Napíšte rovnicu elipsy, ktorá prechádza bodmi A[8, 3], B[6, 4] a stred](https://slidetodoc.com/presentation_image/0adeb80c1c0dd114aa69abe45f194557/image-13.jpg)
- Slides: 13

Analytická geometria kvadratických útvarov Osová rovnica elipsy

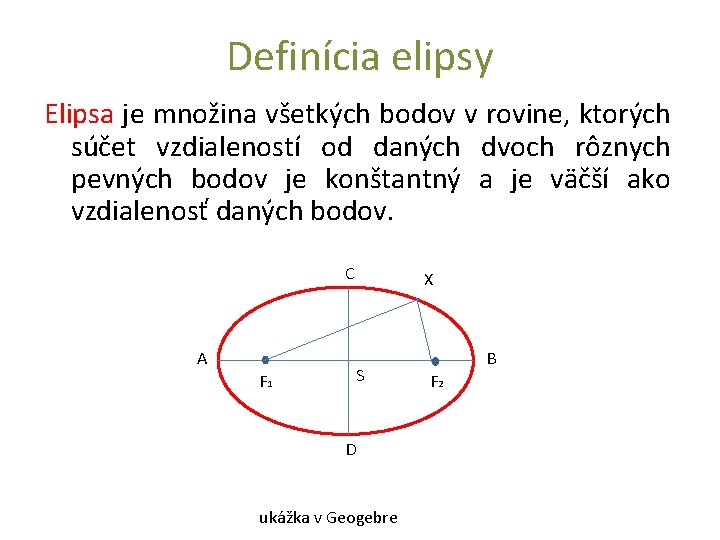
Definícia elipsy Elipsa je množina všetkých bodov v rovine, ktorých súčet vzdialeností od daných dvoch rôznych pevných bodov je konštantný a je väčší ako vzdialenosť daných bodov. C A X S F 1 D ukážka v Geogebre B F 2

Prvky elipsy C b a A F 1 S e B F 2 D • v každej elipse platí vzťah medzi veľkosťami polosí a excentricitou odvodenie • S[m, n] – stred • F 1 F 2 - ohniská A, B – hlavné vrcholy • C, D – vedľajšie vrcholy • X[x, y] – ľubovoľný bod • a = AS = BS - hlavná polos • b = CS = DS - vedľajšia polos • e = F 1 S = F 2 S excentricita(výstrednosť)

Dôležité vzťahy o zvolíme súradnicovú sústavu tak, aby jej začiatok bol v strede elipsy, x-ová os bola hlavná os elipsy a y-ová os bola vedľajšia os. o súradnice význačných bodov budú: S[0, 0] F 1[-e, 0], F 2[e, 0], A[-a, 0], B[a, 0], C[0, b], D[0, -b] C b a A F 1 S e D B F 2

Osová rovnica elipsy Odvodenie • súčet vzdialeností ľubovoľného bodu X od ohnísk je 2 a • postupným odvodzovaním dostaneme rovnicu • Tento vzťah nazývame osová rovnica elipsy

Osová rovnica elipsy Odvodenie • ak stred bude v ľubovoľnom bode súradnicovej sústavy • Tento vzťah nazývame osová rovnica elipsy

Osová rovnica elipsy – riešené príklady Napíšte osovú rovnicu elipsy, ktorá má stred v bode S a polosi a, b.

Osová rovnica elipsy – riešené príklady Z osovej rovnice elipsy určte súradnice stredu a veľkosti polosí elipsy.
![Príklady na precvičenie 1 Napíšte osovú rovnicu elipsy ak a S2 4 a Príklady na precvičenie 1. Napíšte osovú rovnicu elipsy, ak: a) S[2, -4], a =](https://slidetodoc.com/presentation_image/0adeb80c1c0dd114aa69abe45f194557/image-9.jpg)
Príklady na precvičenie 1. Napíšte osovú rovnicu elipsy, ak: a) S[2, -4], a = 10, e = 8 b) S[-1, 2], e = 4, b = 3 c) S[0, 0], b = 3, |F 1 F 2| = 6 2. Zistite všetky prvky elipsy, ak je elipsa daná rovnicou: a) b) c) d) 9 x 2 + 25 y 2 = 225 x 2 + 4 y 2 = 100 4(x – 3)2 + 25(y + 1)2 = 100 3(x + 4)2 + 25(y – 5)2 = 75 3. Napíšte rovnicu elipsy, ktorá prechádza bodmi A[8, 3], B[6, 4] a stred má v začiatku súradnicovej sústavy. (riešenie)

koniec

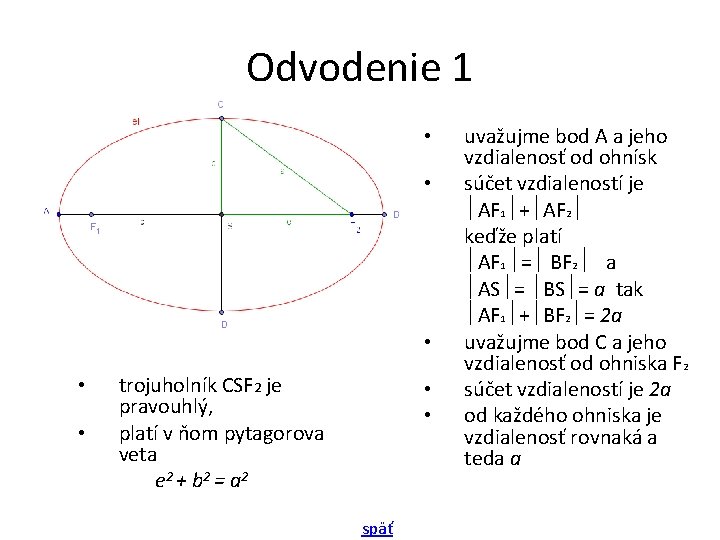
Odvodenie 1 • • • trojuholník CSF 2 je pravouhlý, platí v ňom pytagorova veta e 2 + b 2 = a 2 • • späť uvažujme bod A a jeho vzdialenosť od ohnísk súčet vzdialeností je AF 1 + AF 2 keďže platí AF 1 = BF 2 a AS = BS = a tak AF 1 + BF 2 = 2 a uvažujme bod C a jeho vzdialenosť od ohniska F 2 súčet vzdialeností je 2 a od každého ohniska je vzdialenosť rovnaká a teda a
![Odvodenie 2 S0 0 F 1e 0 F 2e 0 Aa 0 Ba 0 Odvodenie 2 S[0, 0] F 1[-e, 0], F 2[e, 0], A[-a, 0], B[a, 0],](https://slidetodoc.com/presentation_image/0adeb80c1c0dd114aa69abe45f194557/image-12.jpg)
Odvodenie 2 S[0, 0] F 1[-e, 0], F 2[e, 0], A[-a, 0], B[a, 0], C[0, b], D[0, -b] e 2 + b 2 = a 2 späť
![Riešenie 3 Napíšte rovnicu elipsy ktorá prechádza bodmi A8 3 B6 4 a stred Riešenie 3 Napíšte rovnicu elipsy, ktorá prechádza bodmi A[8, 3], B[6, 4] a stred](https://slidetodoc.com/presentation_image/0adeb80c1c0dd114aa69abe45f194557/image-13.jpg)
Riešenie 3 Napíšte rovnicu elipsy, ktorá prechádza bodmi A[8, 3], B[6, 4] a stred má v začiatku súradnicovej sústavy. späť