Analytick geometria kvadratickch tvarov Krunica a priamka Vzjomn






- Slides: 10

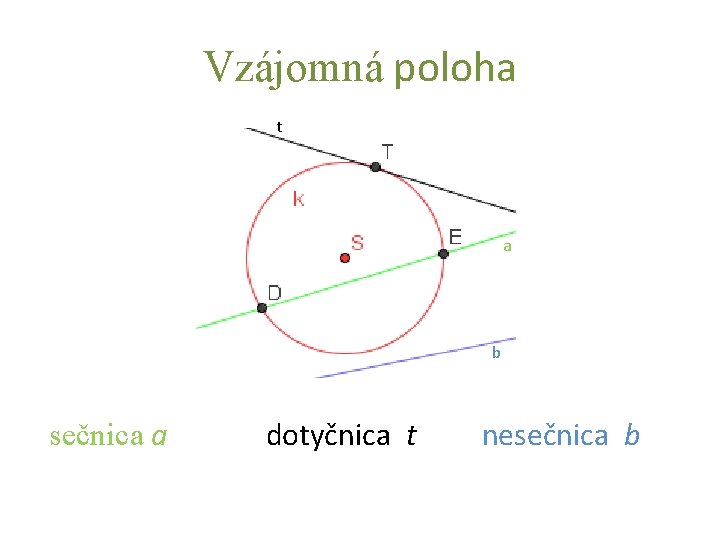
Analytická geometria kvadratických útvarov Kružnica a priamka

Vzájomná poloha t a b sečnica a dotyčnica t nesečnica b

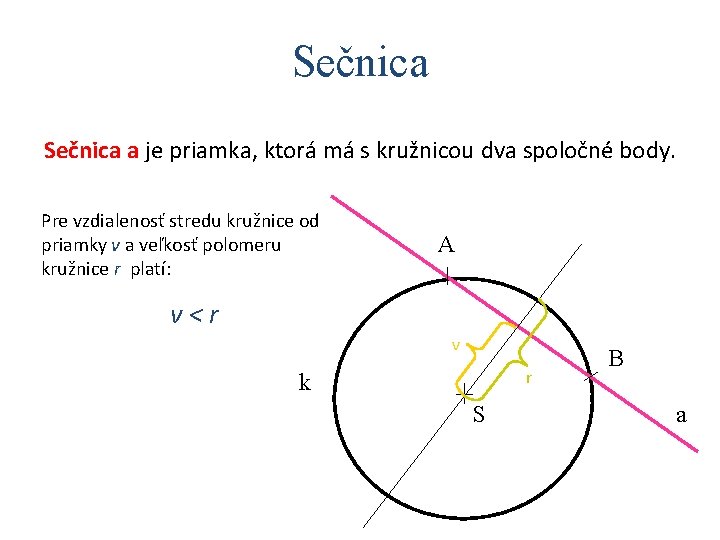
Sečnica a je priamka, ktorá má s kružnicou dva spoločné body. Pre vzdialenosť stredu kružnice od priamky v a veľkosť polomeru kružnice r platí: A v<r v r k S B a

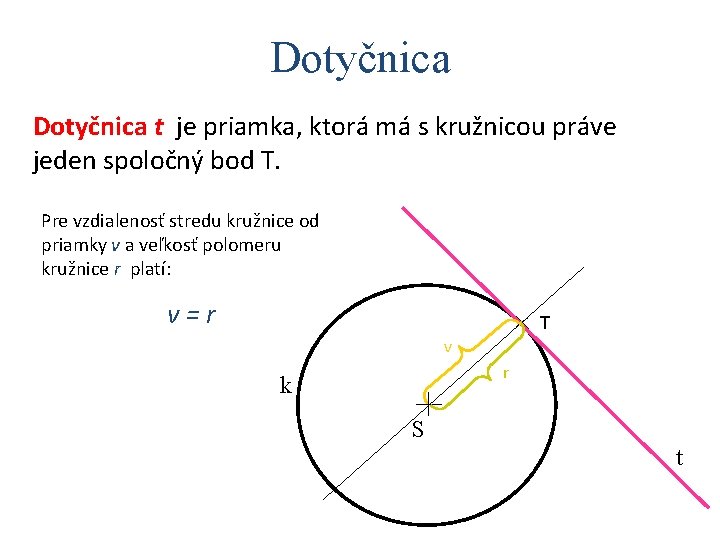
Dotyčnica t je priamka, ktorá má s kružnicou práve jeden spoločný bod T. Pre vzdialenosť stredu kružnice od priamky v a veľkosť polomeru kružnice r platí: v=r T v r k S t

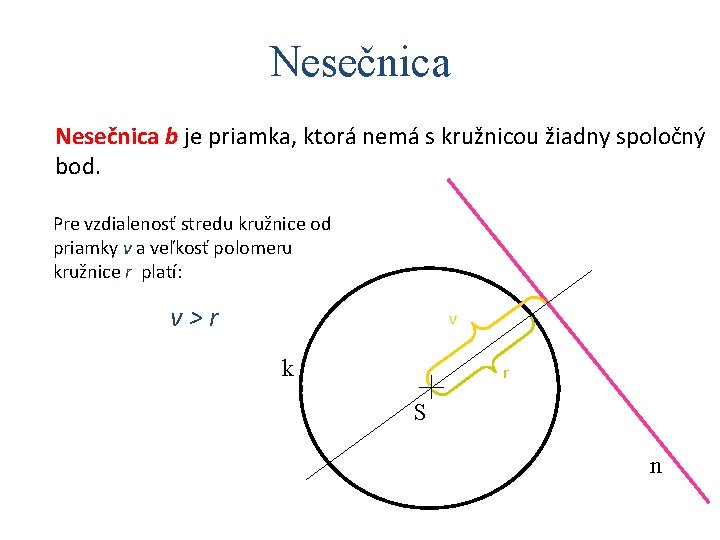
Nesečnica b je priamka, ktorá nemá s kružnicou žiadny spoločný bod. Pre vzdialenosť stredu kružnice od priamky v a veľkosť polomeru kružnice r platí: v>r v k r S n

Riešenie vzájomnej polohy Polohu priamky a kružnice riešime riešením sústavy dvoch rovníc o dvoch neznámych. Jedna je rovnica kružnice k: x 2 + y 2 = r 2. Druhá je rovnica priamky (môže byť všeobecná rovnica aj v smernicovom tvare alebo parametrické vyjadrenie). Rovnicu alebo vyjadrenie priamky dosadíme do rovnice kružnice a upravíme. Dostaneme kvadratickú rovnicu, ktorú štandardne riešime. Podľa hodnoty diskriminantu určíme vzájomnú polohu nasledovne: • D > 0 ide o sečnicu – rovnica má dve riešenia, z ktorých dostaneme súradnice dvoch bodov, v ktorých sa priamka s kružnicou pretína. • D < 0 ide o nesečnicu – rovnica nemá riešenie. • D = 0 ide o dotyčnicu – rovnica má jedno riešenie, pomocou ktorého dostaneme súradnice dotykového bodu.

Vzorové riešenie 1 Určte vzájomnú polohu priamky a kružnice sečnica 4 -3 Získali sme x-ové súradnice priesečníkov, Dosadením za y dostaneme ich y-ové súradnice. Priamka pretína kružnicu v bodoch

Vzorové riešenie 2 Určte vzájomnú polohu priamky a kružnice nesečnica Priamka nepretína kružnicu – je nesečnicou kružnice.

Vzorové riešenie 3 Určte parameter a tak, aby priamka bola dotyčnicou kružnice - z priamky vyjadríme x - dosadíme do rovnice kružnice - umocníme - uložíme v poradí kvadratickej rovnice, v ktorej je neznáma y, z dvoch členov vyjmeme y - vyjadríme diskriminant, ktorý sa pri dotyčnici musí rovnať O - dopočítame a Priamka, ktorá je dotyčnicou kružnice má rovnicu

Príklady na precvičenie 1. Určte vzájomnú polohu priamky a kružnice, ak je dané: a) b) c) Polohu Priamky Kružnice 2. Nájdite také číslo c, že priamka bude dotyčnicou kružnice a) b) c) Tak Riešime Riešením 3. sústavy dvoch rovníc o dvoch neznámych.