ANALYTICAL HIERARCHY PROCESS AHP The Analytic Hierarchy Process

ANALYTICAL HIERARCHY PROCESS (AHP)

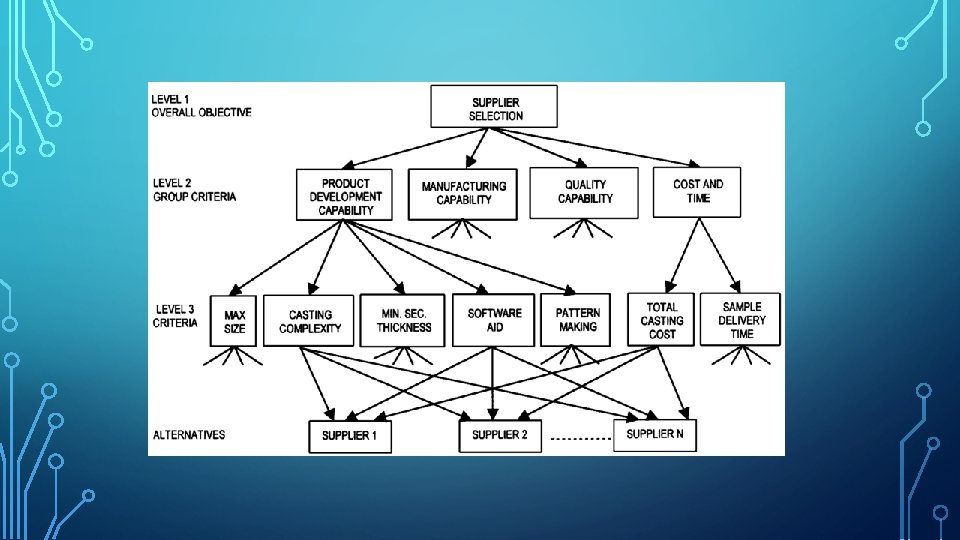
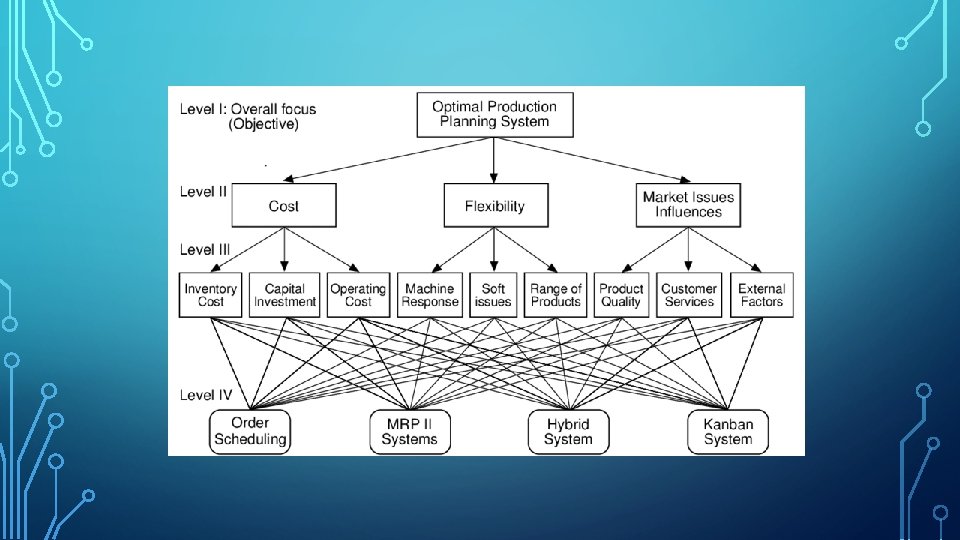
The Analytic Hierarchy Process (AHP) is a method for organizing and analyzing complex decisions, using math and psychology. It was developed by Thomas L. Saaty in the 1970 s and has been refined since then. It contains three parts: the ultimate goal or problem you're trying to solve, all of the possible solutions, called alternatives, and the criteria you will judge the alternatives on. AHP provides a rational framework for a needed decision by quantifying its criteria and alternative options, and for relating those elements to the overall goal.

The Analytic Hierarchy Process is a powerful yet simple method for making decisions. It is commonly used for project prioritization and selection. AHP lets your capture your

Here is the procedure for using Analytical Hierarchy Process: Step 1: Define Alternatives. The AHP process begins by defining the alternatives that need to be evaluated. . Step 2: Define the Problem and Criteria. . Step 3: Establish Priority amongst Criteria Using Pairwise Comparison. . Step 4: Check Consistency. . Step 5: Get the Relative Weights.

STEPS OF IMPLEMENTATION

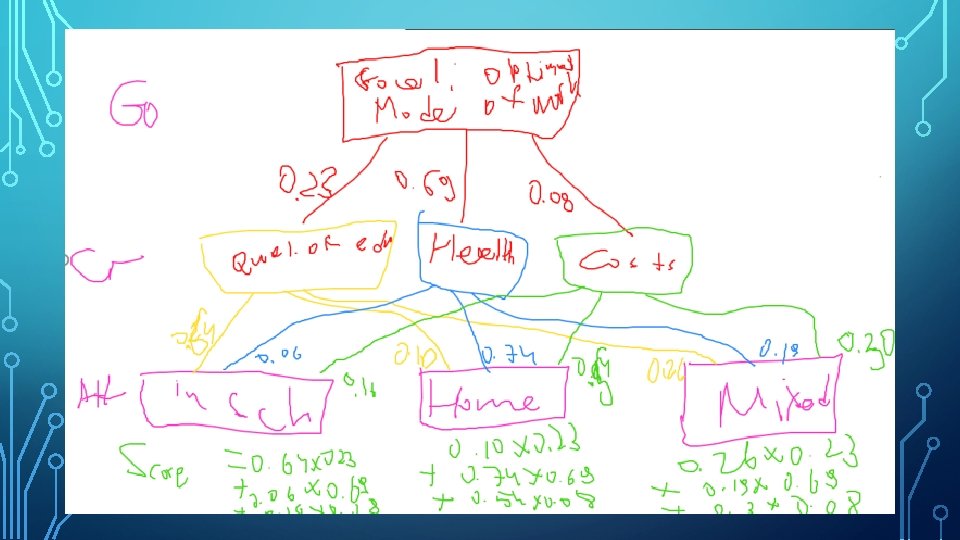
1. DEFINE A PROBLEM WITH A SCOPE To choose the mode of university work under the COVID-19 conditions

2. DEFINE CRITERIA OF SOLUTION (CHOICE) Criteria 1 Quality of education Criteria 2 Criteria 3 Health issues Costs

3. DEFINE ALTERNATIVES Alternative 1 Alternative 2 Alternative 3 Online Offline Mixed (1 year offline)

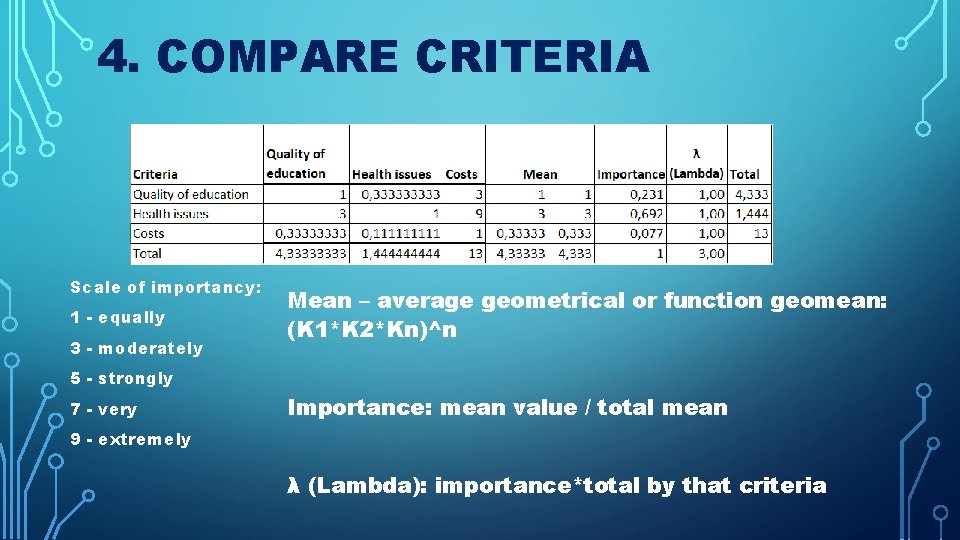
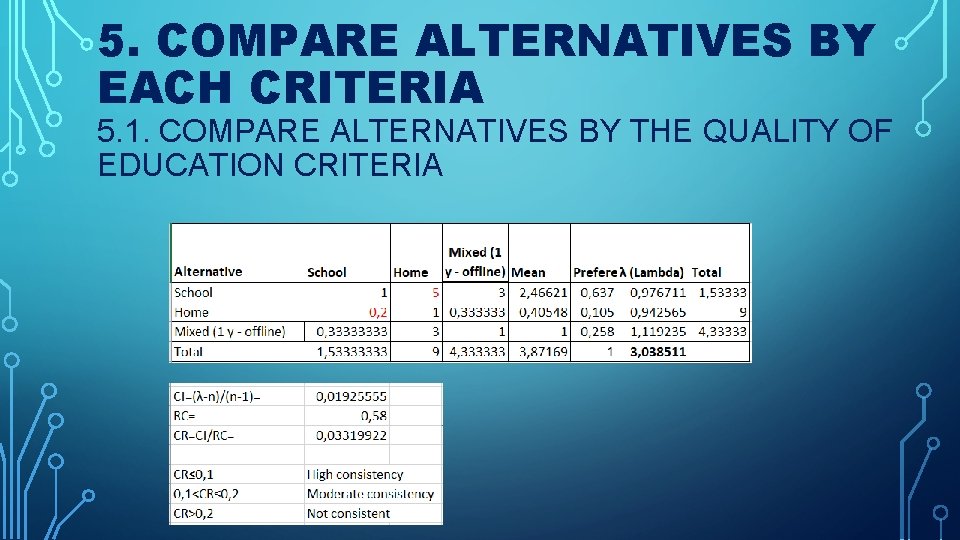
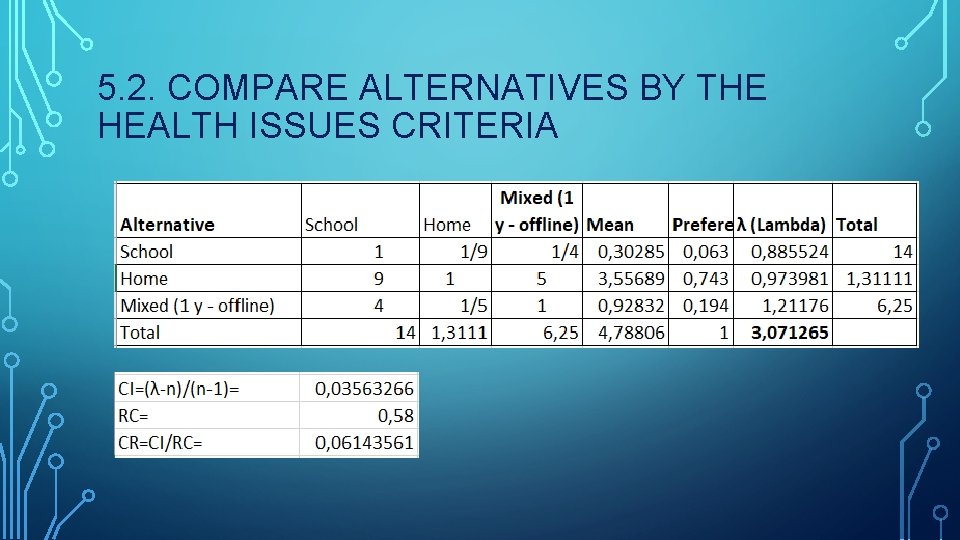
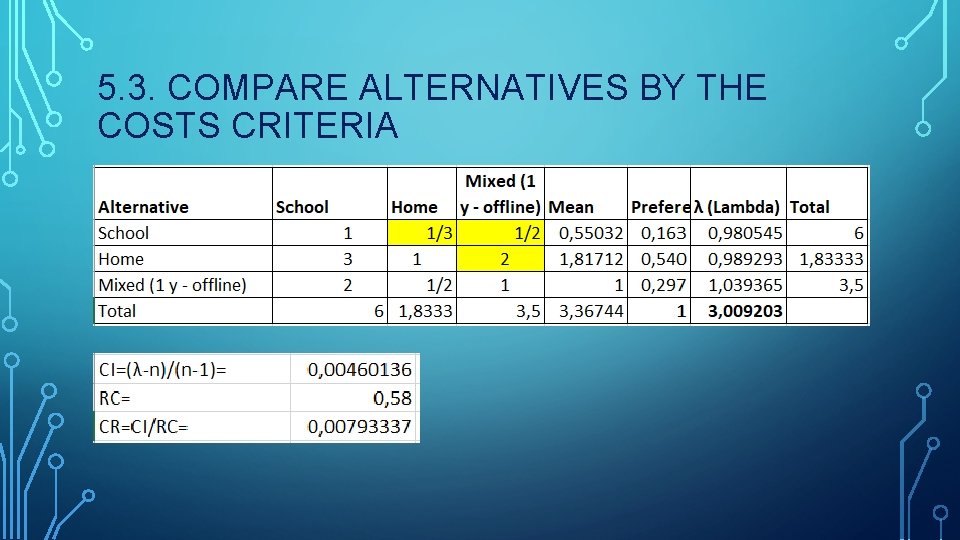
4. COMPARE CRITERIA Scale of importancy: 1 - equally 3 - moderately Mean – average geometrical or function geomean: (K 1*K 2*Kn)^n 5 - strongly 7 - very Importance: mean value / total mean 9 - extremely λ (Lambda): importance*total by that criteria

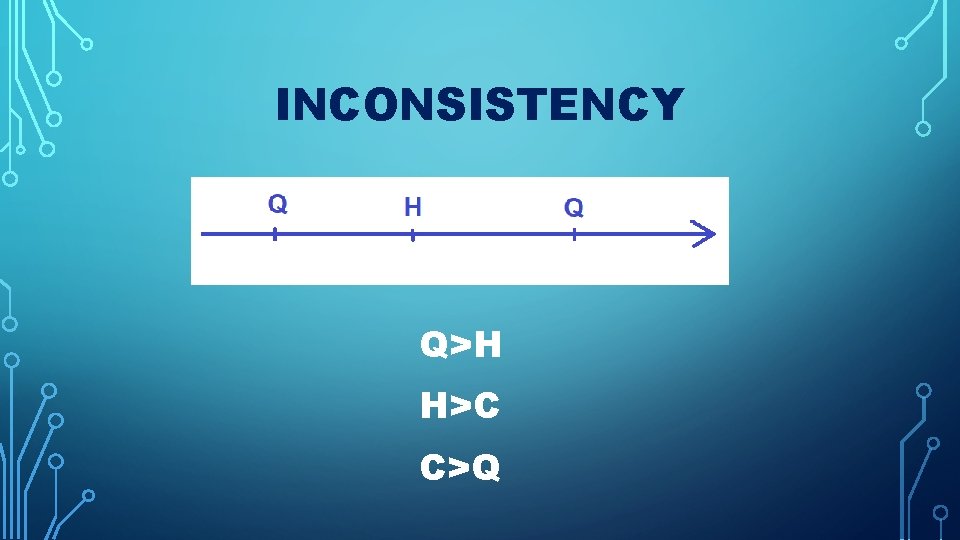
INCONSISTENCY Q>H H>C C>Q

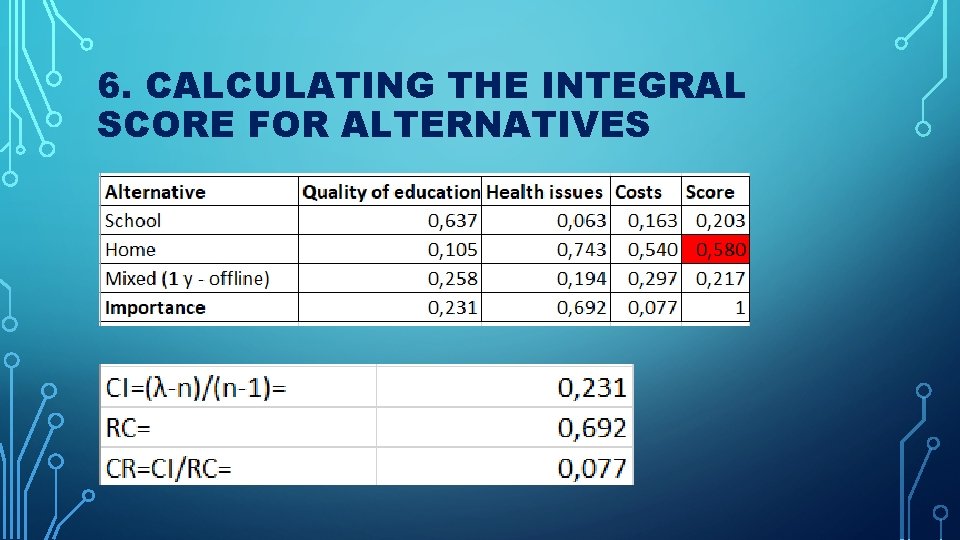
CI=(λ-n)/(n-1)

RANDOM CONSISTANCY reflects the consistency of one’s judgment

CONSISTENCY RATIO (CR) CR=CI / RC In practice, a CR of 0. 1 or below is considered acceptable. Any higher value at any level indicate that the judgments warrant re-judge. CR≤ 0, 1 High consistency 0, 1<CR≤ 0, 2 Moderate consistency CR>0, 2 Not consistent

5. COMPARE ALTERNATIVES BY EACH CRITERIA 5. 1. COMPARE ALTERNATIVES BY THE QUALITY OF EDUCATION CRITERIA

5. 2. COMPARE ALTERNATIVES BY THE HEALTH ISSUES CRITERIA

5. 3. COMPARE ALTERNATIVES BY THE COSTS CRITERIA

6. CALCULATING THE INTEGRAL SCORE FOR ALTERNATIVES