ANALYTICAL APPROACH TO CUSTOM DATAPATH SYNTHESIS Serkan Askar

ANALYTICAL APPROACH TO CUSTOM DATAPATH SYNTHESIS Serkan Askar, Maciej Ciesielski Department of Electrical & Computer Engineering University of Massachusetts, Amherst {saskar, ciesiel}@ecs. umass. edu © 2000 M. Ciesielski Datapath Synthesis 1

Outline • • • Introduction Problem definition Approach, design phases Analytical formulation (MILP) Results Conclusions and future work © 2000 M. Ciesielski Datapath Synthesis 2

Motivation • Datapath: highly regular structure – array of bit/row slices – rows: identical cells – hand-crafted layout Datapath cell • Limitations of custom design – ability of the designer – slow development time power rails © 2000 M. Ciesielski Datapath Synthesis 3

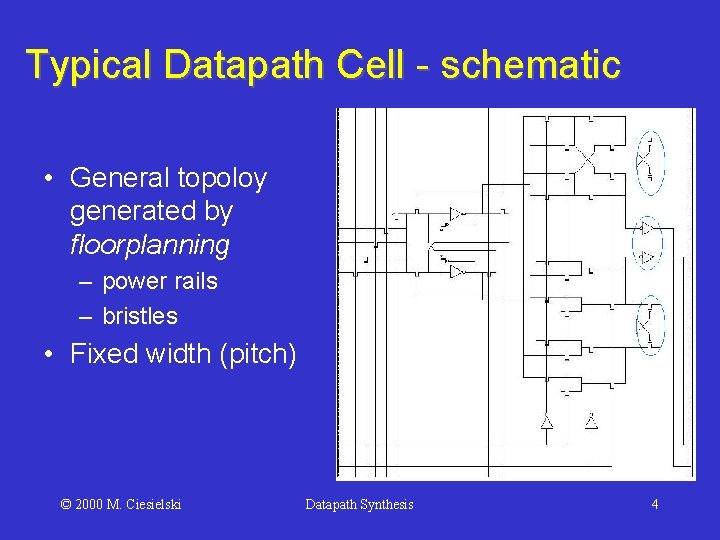
Typical Datapath Cell - schematic • General topoloy generated by floorplanning – power rails – bristles • Fixed width (pitch) © 2000 M. Ciesielski Datapath Synthesis 4

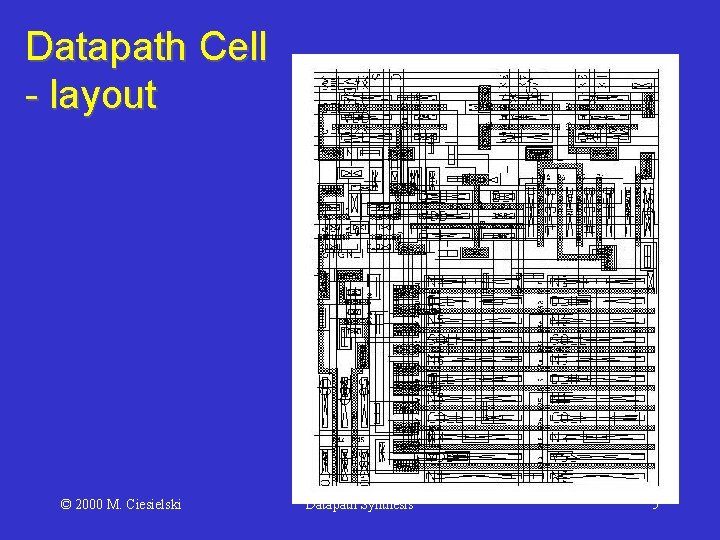
Datapath Cell - layout © 2000 M. Ciesielski Datapath Synthesis 5

Problem Definition • Automation of transistor level placement – diffusion-limited, routing ignored (to certain degree) • Goal: – minimize layout area, size – improve manufacturability, routability • Constraints – bit-slice constraints – component constraints – custom design issues © 2000 M. Ciesielski Datapath Synthesis fixed 6

Previous Work • Very little work on custom quality datapath synthesis • Stochastic methods – simulated annealing – genetic algorithms • Deterministic methods – analytical (QP, ILP, etc) – constructive methods © 2000 M. Ciesielski Datapath Synthesis 7

Bit-slice Constraints data lines • Fixed width (pitch) – power rails • Vertical bristles – data lines • Horizontal bristles – control lines VDD GND control lines pitch © 2000 M. Ciesielski Datapath Synthesis 8

Component Types • Transistors, logic gates • Transistor chains, folded transistors © 2000 M. Ciesielski Datapath Synthesis 9

Component Geometries Rectangular © 2000 M. Ciesielski L-shape Datapath Synthesis 10

Custom Design Issues • Multiple instances – chaining, folding • Merging (same diffusion type, sharing common net) – diffusion sharing (same cell) © 2000 M. Ciesielski Datapath Synthesis 11

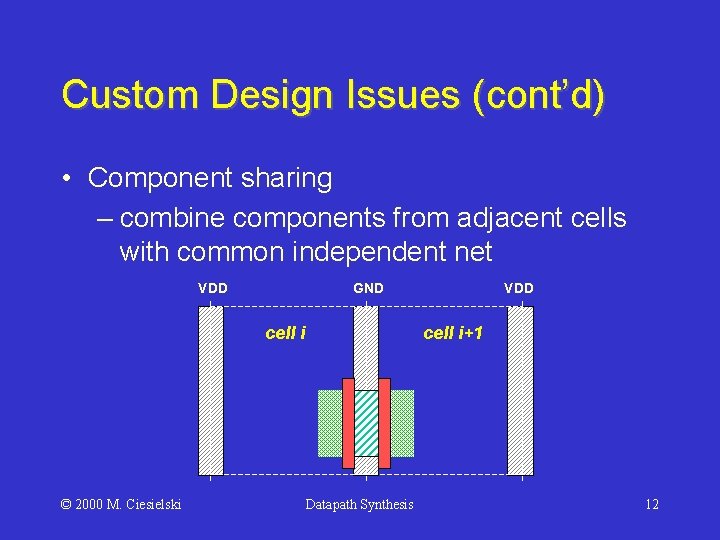
Custom Design Issues (cont’d) • Component sharing – combine components from adjacent cells with common independent net VDD GND cell i © 2000 M. Ciesielski VDD cell i+1 Datapath Synthesis 12

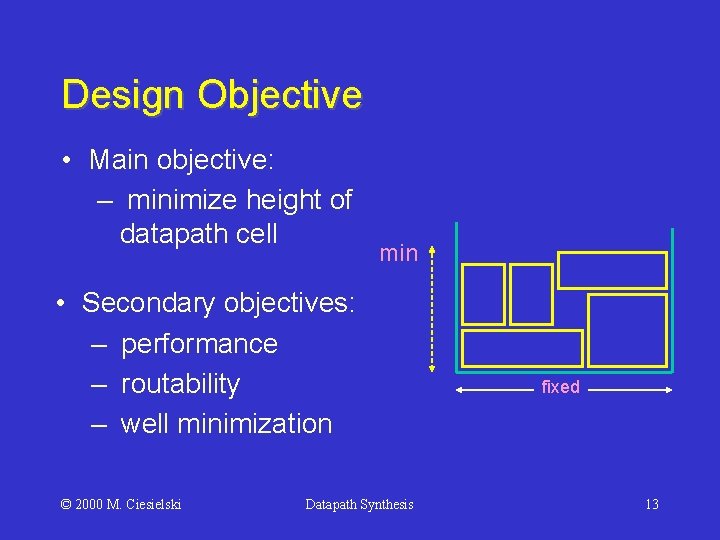
Design Objective • Main objective: – minimize height of datapath cell min • Secondary objectives: – performance – routability – well minimization © 2000 M. Ciesielski Datapath Synthesis fixed 13

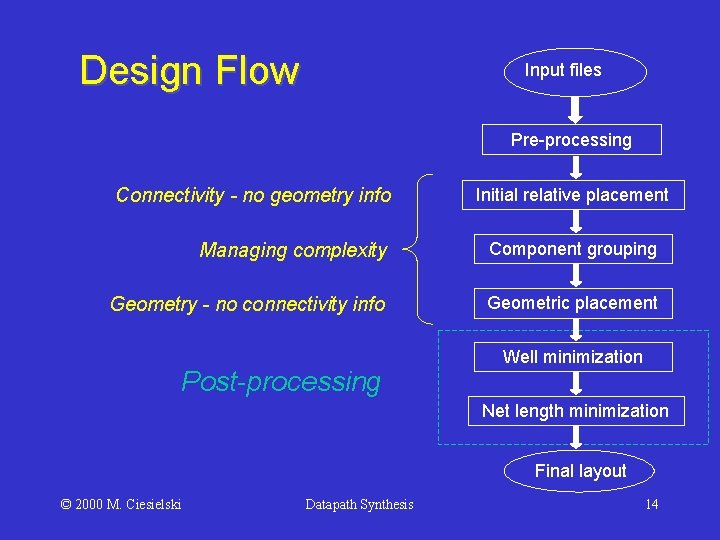
Design Flow Input files Pre-processing Connectivity - no geometry info Initial relative placement Managing complexity Component grouping Geometry - no connectivity info Geometric placement Post-processing Well minimization Net length minimization Final layout © 2000 M. Ciesielski Datapath Synthesis 14

Pre-processing • Connectivity analysis • Initial component merging (to minimize number of objects to place) © 2000 M. Ciesielski Datapath Synthesis 15

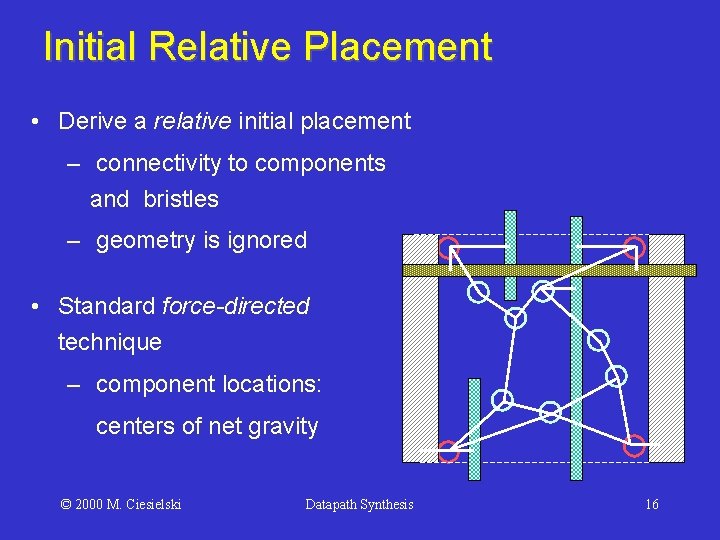
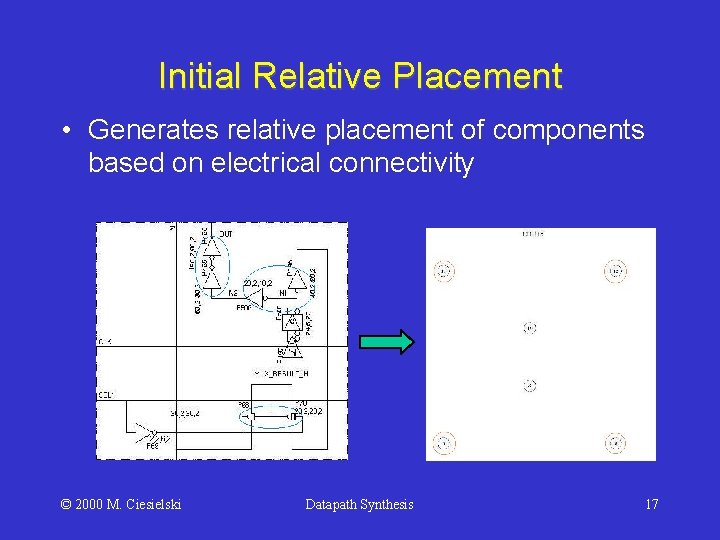
Initial Relative Placement • Derive a relative initial placement – connectivity to components and bristles – geometry is ignored • Standard force-directed technique – component locations: centers of net gravity © 2000 M. Ciesielski Datapath Synthesis 16

Initial Relative Placement • Generates relative placement of components based on electrical connectivity © 2000 M. Ciesielski Datapath Synthesis 17

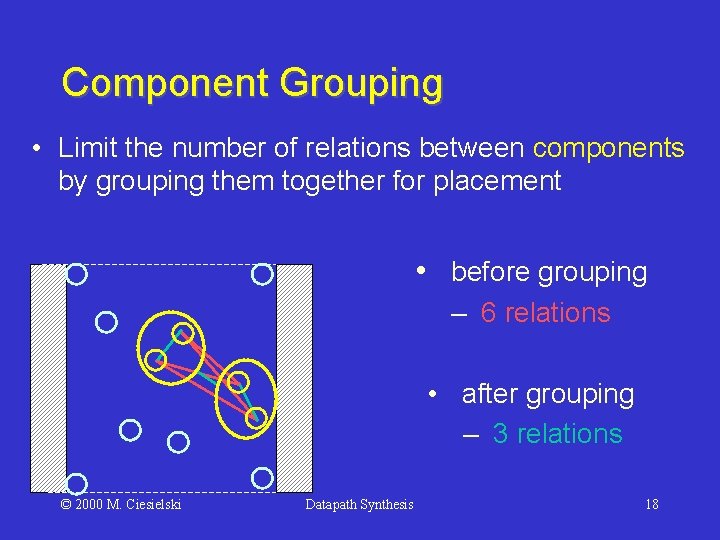
Component Grouping • Limit the number of relations between components by grouping them together for placement • before grouping – 6 relations • after grouping – 3 relations © 2000 M. Ciesielski Datapath Synthesis 18

Geometric Placement • Generate non-overlapping placement – component geometry – design rules – fixed connectivity (initial relative placement) • Model: Mixed Integer Linear Program (MILP) © 2000 M. Ciesielski Datapath Synthesis 19

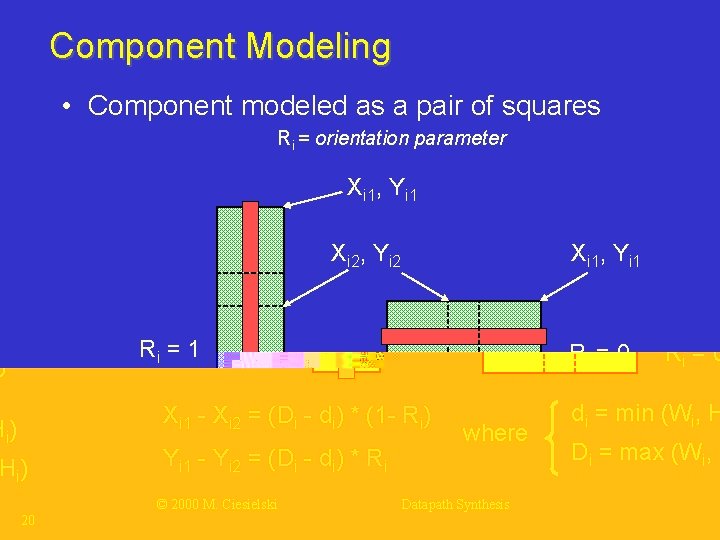
Component Modeling • Component modeled as a pair of squares Ri = orientation parameter Xi 1, Yi 1 Xi 2, Yi 2 Ri = 1 Ri = 0 Xi 1 - Xi 2 = (Di - di) * (1 - Ri) Yi 1 - Yi 2 = (Di - di) * Ri © 2000 M. Ciesielski Xi 1, Yi 1 where Datapath Synthesis di = min (Wi, Hi) Di = max (Wi, Hi) 20

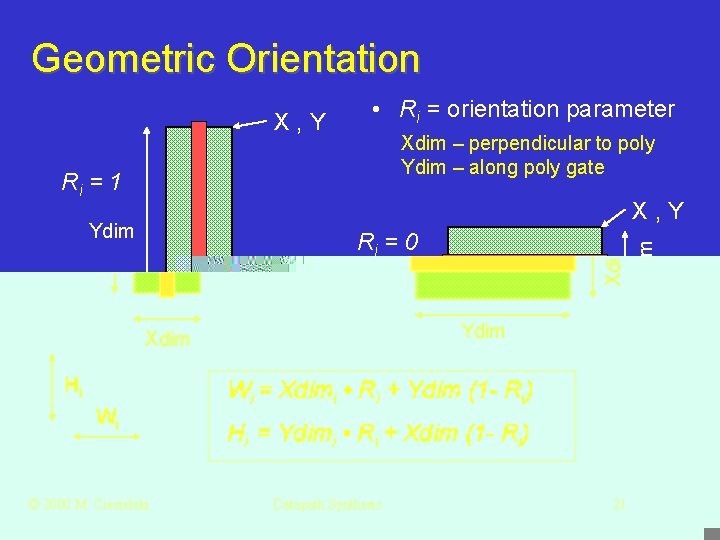
Geometric Orientation X, Y Ri = 1 • Ri = orientation parameter Xdim – perpendicular to poly Ydim – along poly gate X, Y Ydim Xdim Hi Wi © 2000 M. Ciesielski Xdim Ri = 0 Wi = Xdimi • Ri + Ydim (1 - Ri) Hi = Ydimi • Ri + Xdim (1 - Ri) Datapath Synthesis 21

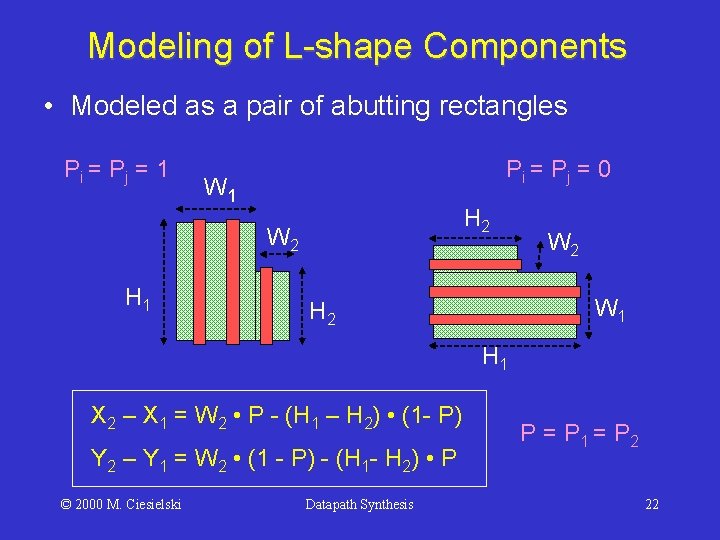
Modeling of L-shape Components • Modeled as a pair of abutting rectangles Pi = Pj = 1 Pi = Pj = 0 W 1 H 2 W 2 H 1 W 2 W 1 H 2 H 1 X 2 – X 1 = W 2 • P - (H 1 – H 2) • (1 - P) Y 2 – Y 1 = W 2 • (1 - P) - (H 1 - H 2) • P © 2000 M. Ciesielski Datapath Synthesis P = P 1 = P 2 22

Selection of Component Instances • Selection parameter, Si (k = 2 instances) Si = 0 Si = 1 • Easy extension to arbitrary k. © 2000 M. Ciesielski Datapath Synthesis 23

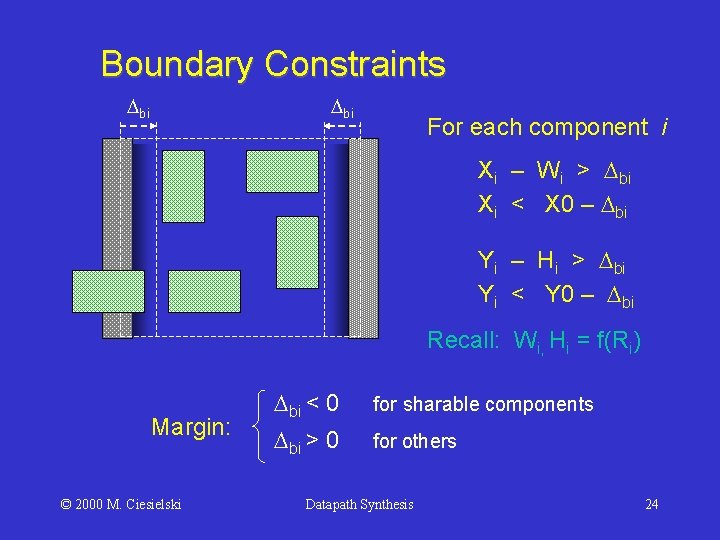
Boundary Constraints bi For each component i Xi – Wi > bi Xi < X 0 – bi Yi – Hi > bi Yi < Y 0 – bi Recall: Wi, Hi = f(Ri) Margin: © 2000 M. Ciesielski bi < 0 for sharable components bi > 0 for others Datapath Synthesis 24

Non-overlapping Constraints • Binary variable Qij = 0 (vert), = 1 (horiz) j Qij = 0 i Qij = 1 j Xj - Xi >= Dim. Xj - L * (1 - Qij) + sep Yj - Yi >= Dim. Yj - L * Qij + sep © 2000 M. Ciesielski Datapath Synthesis 25

Optimization Problem (MILP) • Minimize – the cell height, Y 0 • Subject to – boundary constraints – non-overlapping constraints – component shape constraints – component selection constraints © 2000 M. Ciesielski Datapath Synthesis fixed 26

Sample Flow © 2000 M. Ciesielski Datapath Synthesis 27

Final layout © 2000 M. Ciesielski Datapath Synthesis 28

MILP: Complexity Issues • Reduce number of placeable components and variables – merging (pre-processing) • Reduce number of integer variables – component grouping QAB Qxy = QAB for x A and y B Group A © 2000 M. Ciesielski Datapath Synthesis Group B 29

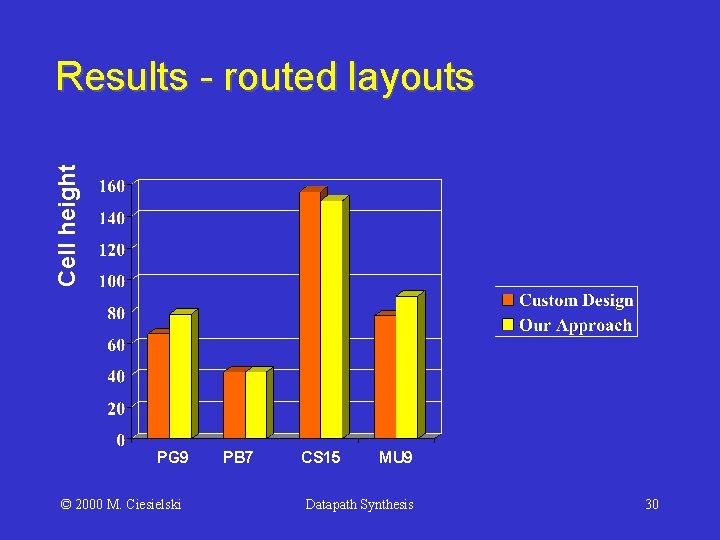
Cell height Results - routed layouts PG 9 © 2000 M. Ciesielski PB 7 CS 15 MU 9 Datapath Synthesis 30

Conclusion & Future Work • Automation of datapath layout – fast – within acceptable area overhead (5 - 10%) • • Post-processing Iterative improvement Hierarchical placement Grouping algorithm © 2000 M. Ciesielski Datapath Synthesis 31

Post-processing • Improve the result of geometric placement • Well minimization: improve manufacturability • Mirroring along both axes • Efficient MILP model and formulation • Net length minimization: simplify routing • Mirroring along both axes • Constrained optimization problem • Simple but effective MILP model and formulation © 2000 M. Ciesielski Datapath Synthesis 32

Post-processing – Net length minimization • Mirroring • Swapping • Moving – Well minimization • Mirroring – Layout compaction © 2000 M. Ciesielski Datapath Synthesis 33

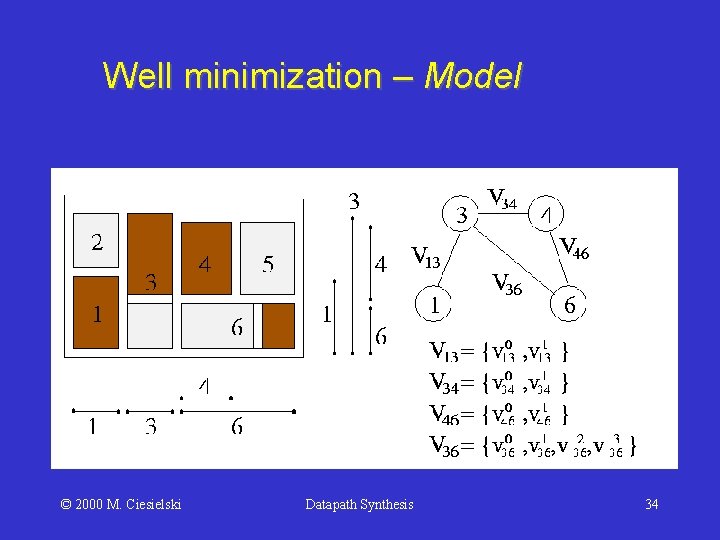
Well minimization – Model © 2000 M. Ciesielski Datapath Synthesis 34

Well minimization – overlap weights • Mirroring affects the overlap weights © 2000 M. Ciesielski Datapath Synthesis 35

Well minimization – Formulation • Objective: Max • subject to (i, j) Zij = (1 - mi - mj + mij) vij 0 + (mi - mij) vij 1 + (mj - mij) vij 2 + mij vij 3 where mi = 1 0 © 2000 M. Ciesielski if i is mirrored otherwise Datapath Synthesis mij = mi AND mj mij <= mi mij <= mj mij mi + mj - 1 36

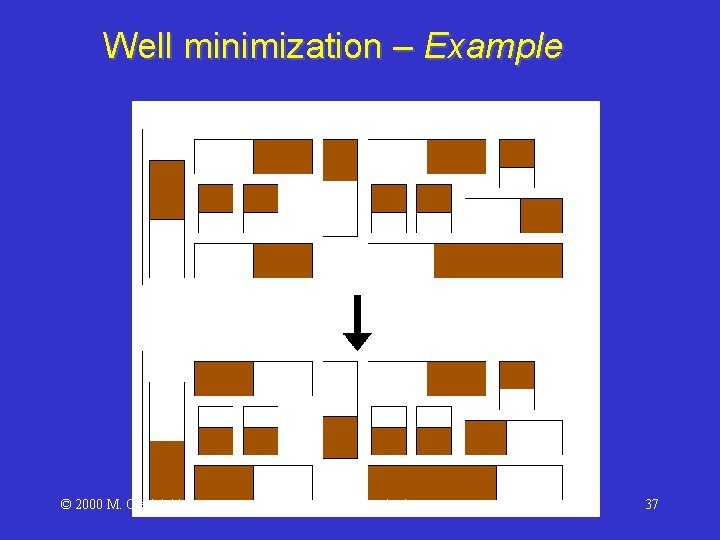
Well minimization – Example © 2000 M. Ciesielski Datapath Synthesis 37

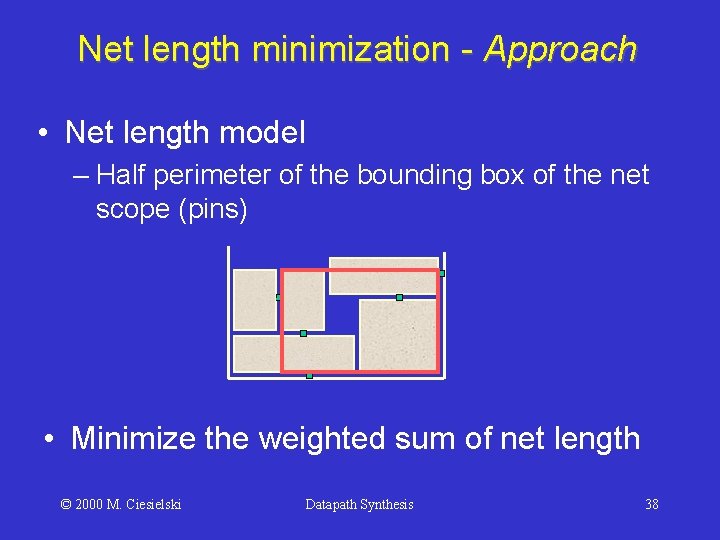
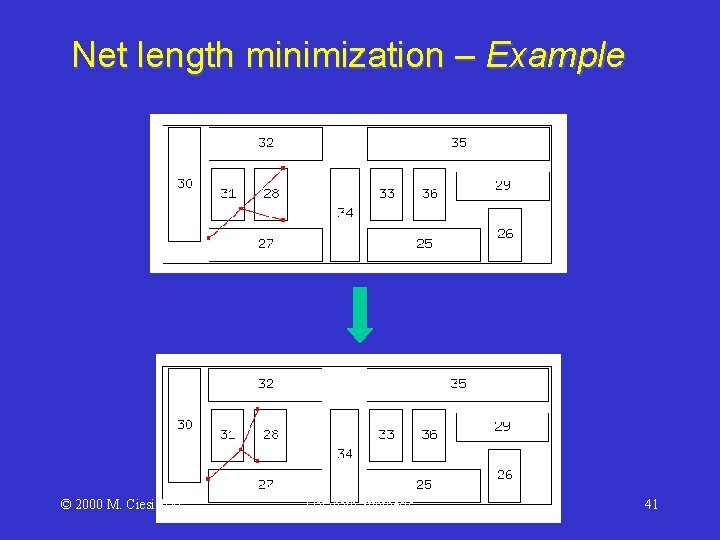
Net length minimization - Approach • Net length model – Half perimeter of the bounding box of the net scope (pins) • Minimize the weighted sum of net length © 2000 M. Ciesielski Datapath Synthesis 38

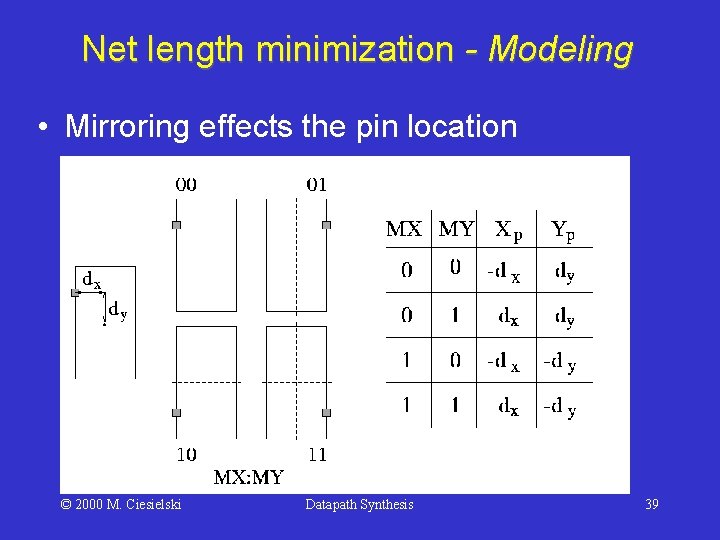
Net length minimization - Modeling • Mirroring effects the pin location © 2000 M. Ciesielski Datapath Synthesis 39

Net length minimization - Formulation • Objective: Min Li i Nets • subject to Xpj = Xcq - (1 - Mxq - Myq + Mxyq) dx + (Mxq – Mxyq) dx (Myq – Mxyq) dx + Mxyq dx where: j Pins, q Comps, Mxy = Mx AND My Xcq = center coordinate of component q © 2000 M. Ciesielski Datapath Synthesis 40

Net length minimization – Example © 2000 M. Ciesielski Datapath Synthesis 41

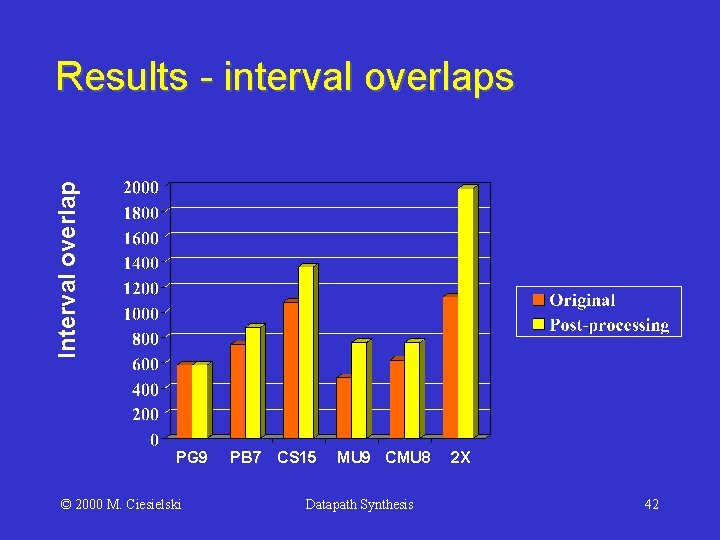
Interval overlap Results - interval overlaps PG 9 © 2000 M. Ciesielski PB 7 CS 15 MU 9 CMU 8 Datapath Synthesis 2 X 42

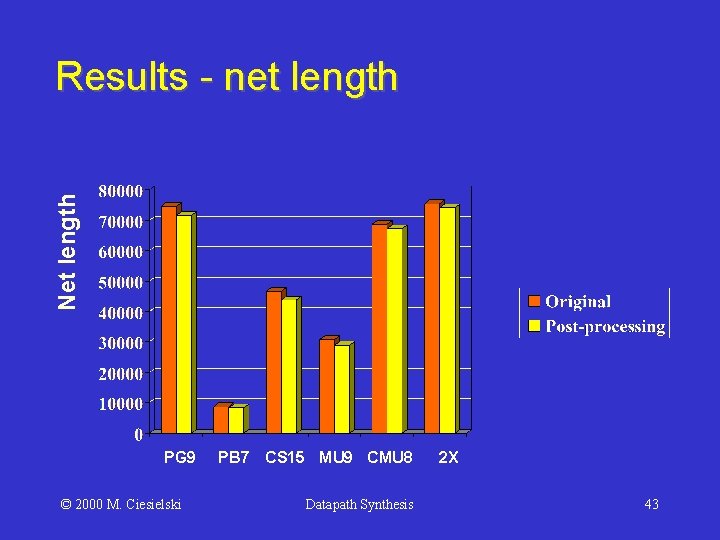
Net length Results - net length PG 9 © 2000 M. Ciesielski PB 7 CS 15 MU 9 CMU 8 Datapath Synthesis 2 X 43

Conclusions & Future Work • Automation of datapath layout – fast within acceptable area overhead • Improvement – routability, manufacturability – delay, area • • Component swapping Global routing phase after post-processing Iterative group relaxation Efficient algorithms for grouping © 2000 M. Ciesielski Datapath Synthesis 44