Analysis Using SPSS for windows Part II Multivariate

Analysis Using SPSS for windows Part II Multivariate analysis Negussie Deyessa, MD, MPH, PHD Aug 2015

Multivariate Analysis • It is the 3 rd Step in data analysis • MULTIvariate analysis is the process of examining the effects of two or more independent variable on the dependent variable simultaneously • Multivariate analysis allows us to: – Control for alternative effects and thus assess the extent of spuriousness (confounding, mediating and interacting effect) – Conducts definitive test of our hypotheses – Gains a more sophisticated view of social reality Negussie D. 2012 2

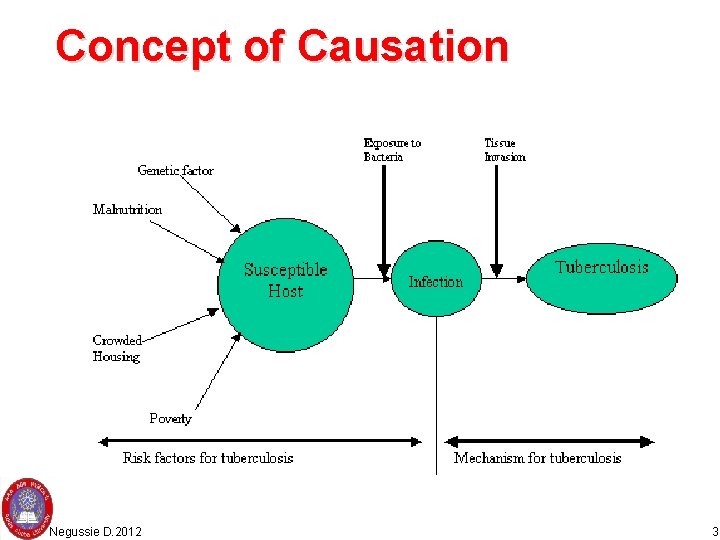
Concept of Causation Negussie D. 2012 3

Multivariate analysis Independent variables (two or more) Dependent variable (single) Nominal (binary) Some Nominal (binary or/ & non-binary) and Continuous of different forms or Continuous 4 Negussie D. 2012

Cont… • Analysis depends on type of variable of the dependent variable • The dependent variable can be nominal (usually dichotomous) – Binary logistic regression • The dependent variable could also be continuous variable – Linear regression Negussie D. 2012 5

Multivariate analysis • What to think during analysis: 1. Which of the independent variables are good enough to show effect on the dependant variable (Model fit)? 2. How much is the effect of the independent variables on the dependant variable (R 2)? 3. How much is the effect of individual variables (independent association, interaction, mediating etc) on the dependant variable? Negussie D. 2012 6

Dependent Variable Crude association – When single predictor and an out come are tested for presence of an association. Adjusted association – When two or more predictors and an out come are tested for presence of an association and their individual main effect. – By adjusting predictors, we can find possible main effects, confounders, mediators, interaction effect. Negussie D. 2012 7

Binary Dependent Variable Adjusted using Logistic regression Analysis Regression Binary logistic – It is the most commonly used to adjust for explanatory variables, adjusting for about 10 to 15 variables depending on sample size. – The same procedure as in analyzing for crude analysis using binary logistic regression. – Transfer the dependent variable to the “dependent” and the predictor variables (all (usually less than 10 -15) possible predictor variables) to the “Covariates”. Negussie D. 2012 8

Analysis Regression Binary logistic Negussie D. 2012 9

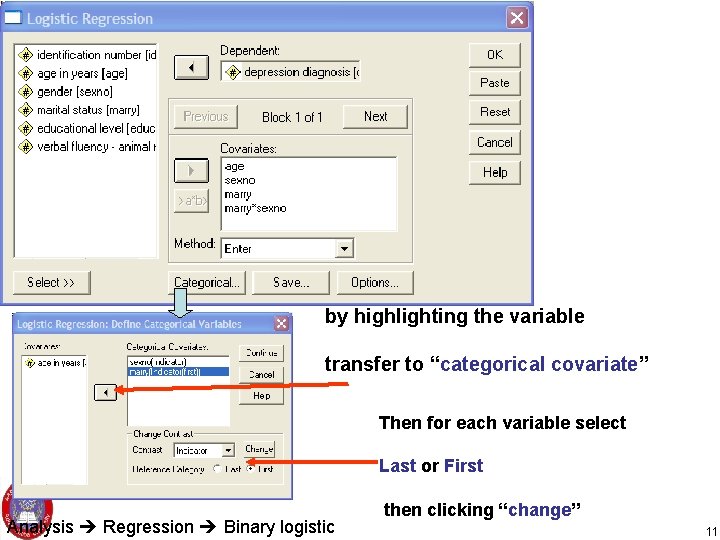
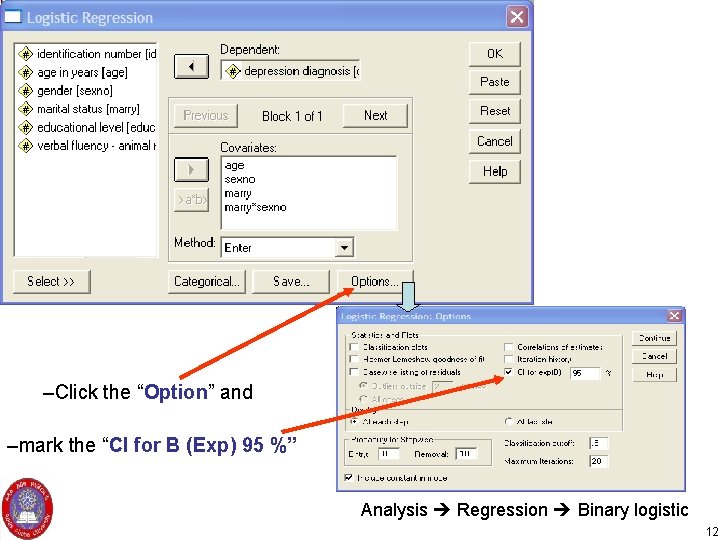
Cont… • The predictor Variable can be transferred step by step thus you are able to see individual and interaction effect step by step. • If there is predictor variable that is categorical click the categorical and by highlighting all categorical variable transfer to “categorical covariate” and for each variables choose cautiously the reference option (first or last) by ticking and clicking change continue. • To look for an interaction effect of two variables you should transfer variables both shaded and transfer using >a*b> or • Click the “Option” and mark the “CI for B (Exp) 95 %” Negussie D. 2012 10

by highlighting the variable transfer to “categorical covariate” Then for each variable select Last or First Analysis Regression Binary logistic then clicking “change” 11

–Click the “Option” and –mark the “CI for B (Exp) 95 %” Analysis Regression Binary logistic 12

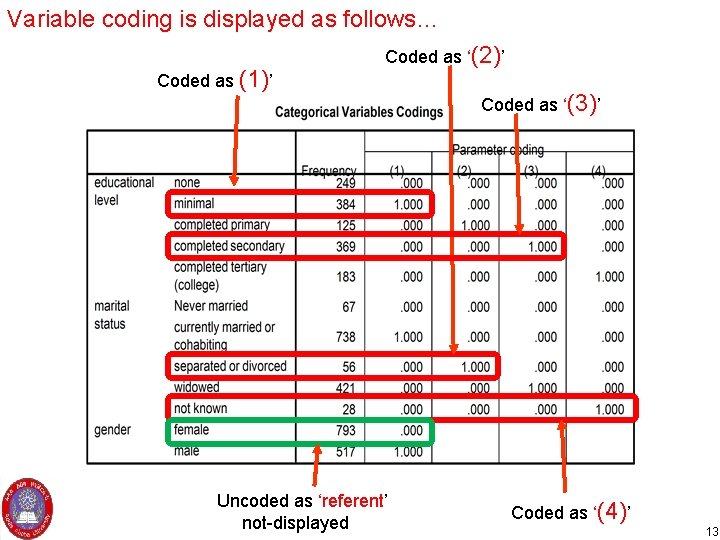
Variable coding is displayed as follows… Coded as (1)’ Coded as ‘(2)’ Uncoded as ‘referent’ not-displayed Coded as ‘(3)’ Coded as ‘(4)’ 13

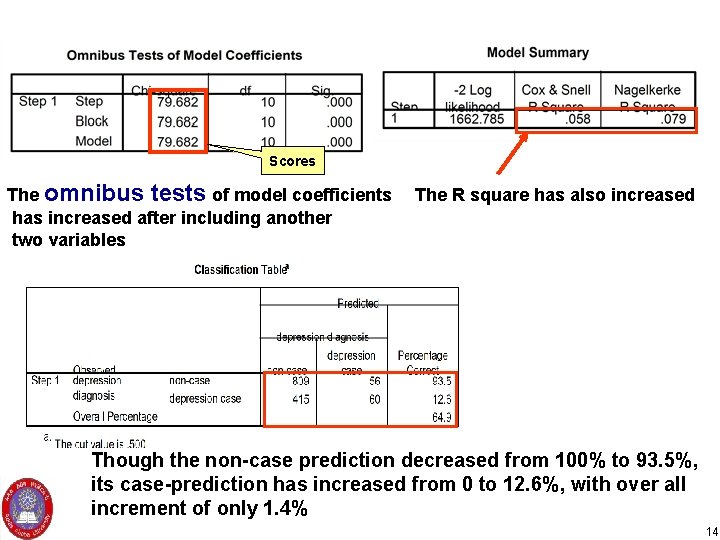
Scores The omnibus tests of model coefficients has increased after including another two variables The R square has also increased Though the non-case prediction decreased from 100% to 93. 5%, its case-prediction has increased from 0 to 12. 6%, with over all increment of only 1. 4% 14

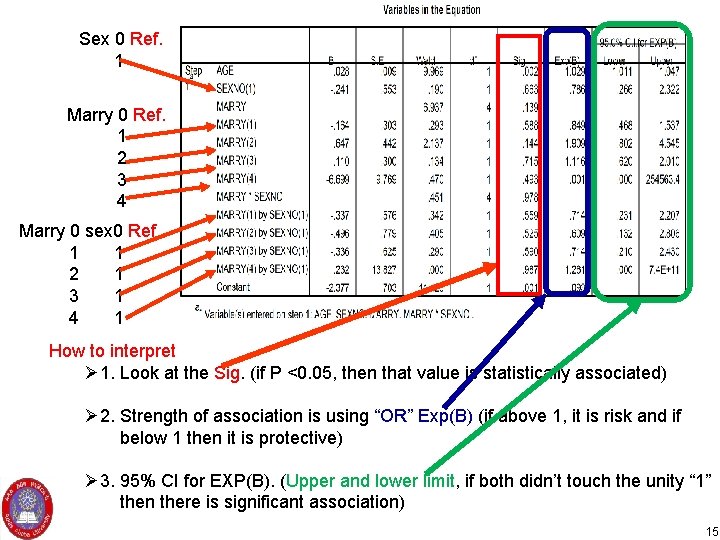
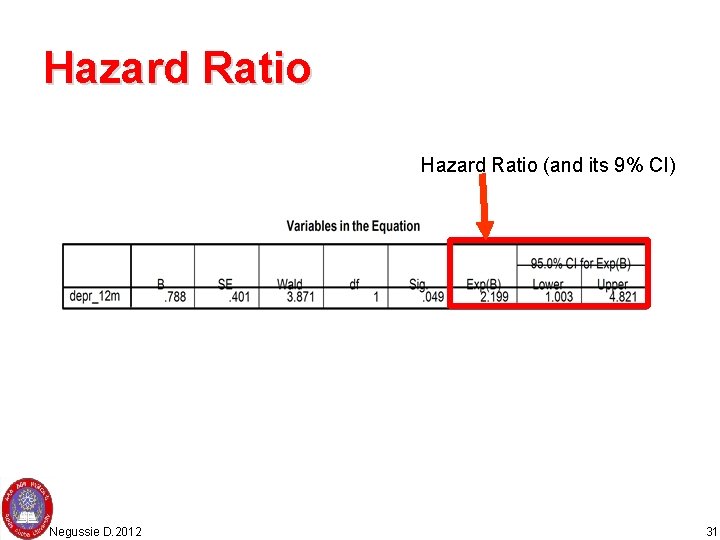
Sex 0 Ref. 1 Marry 0 Ref. 1 2 3 4 Marry 0 sex 0 Ref. 1 1 2 1 3 1 4 1 How to interpret Ø 1. Look at the Sig. (if P <0. 05, then that value is statistically associated) Ø 2. Strength of association is using “OR” Exp(B) (if above 1, it is risk and if below 1 then it is protective) Ø 3. 95% CI for EXP(B). (Upper and lower limit, if both didn’t touch the unity “ 1” then there is significant association) 15

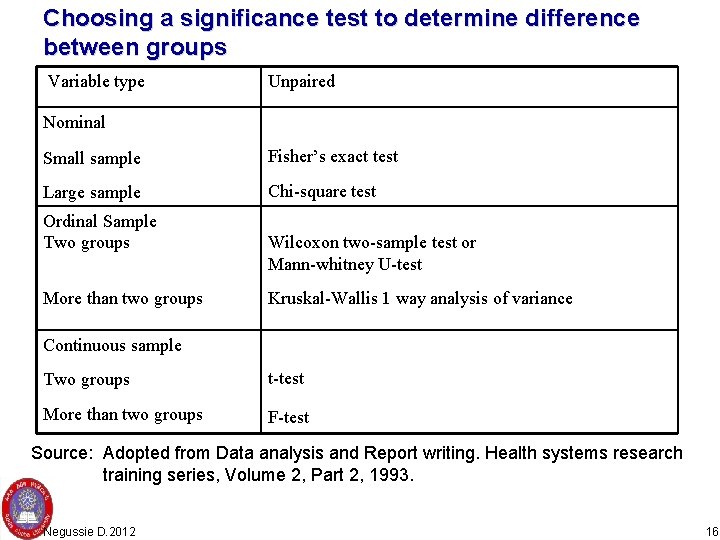
Choosing a significance test to determine difference between groups Variable type Unpaired Nominal Small sample Fisher’s exact test Large sample Chi-square test Ordinal Sample Two groups More than two groups Wilcoxon two-sample test or Mann-whitney U-test Kruskal-Wallis 1 way analysis of variance Continuous sample Two groups t-test More than two groups F-test Source: Adopted from Data analysis and Report writing. Health systems research training series, Volume 2, Part 2, 1993. Negussie D. 2012 16

Survival analysis

Survival analysis • The main outcome under assessment of cancer researches is the time to an event of interest. • The generic name for the time is survival time, • In many medical studies, time to death is the event of interest. • Censoring and event are terminologies used in the analysis Negussie D. 2012 18

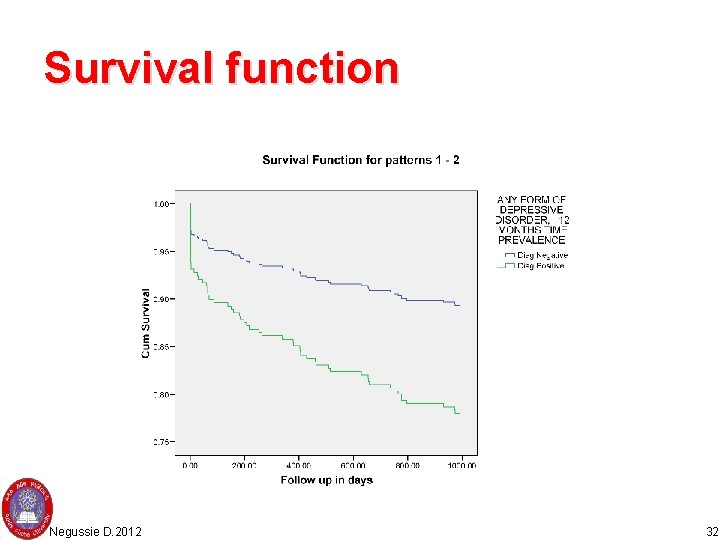
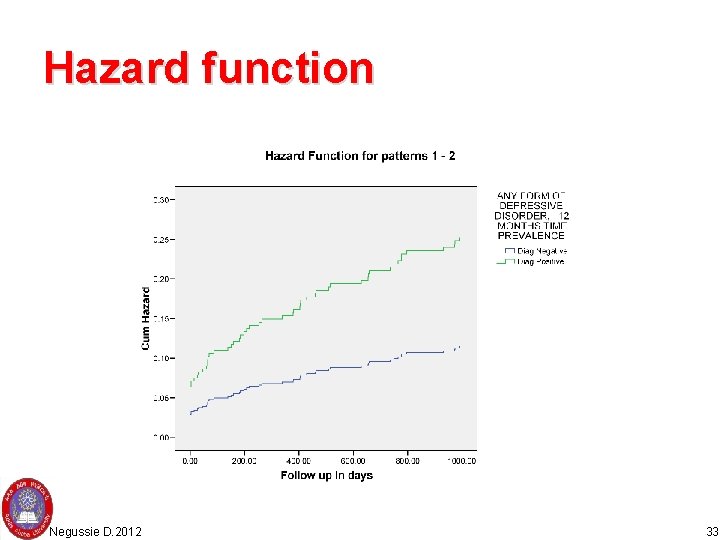
Hazard and survival • Survival data are described in terms of two probabilities, Hazard and Survival • Survival is probability that an individual survives from time origin (e. g. diagnosis of cancer) to a specified future time. • In contrast to the survivol function, which focuses on not having an event, the hazard function focuses on the event occurring. Negussie D. 2012 19

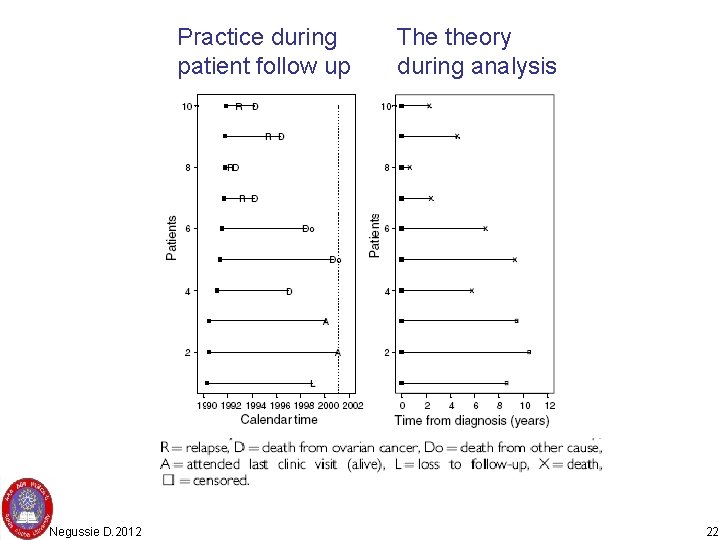
Censoring and event • A person is counted as censored if he/she completed the time of study with out the event or if he out-migrated the study area before completing the study • A person is counted as an event if he/she acquired the event of interest • All study subjects (both exposed/ unexposed) are usually followed up till the end of study time to be categorized to censored or event Negussie D. 2012 20

Three methods • Life table method: a Method using probability of occurrence during a range of time intervals • Kaplan-meier method: it is a method that depicts the probability of the event as the event happens • Cox-regression: it is similar to Kaplan-meier method but using different categories as in a regression during analysis Negussie D. 2012 21

Practice during patient follow up Negussie D. 2012 The theory during analysis 22

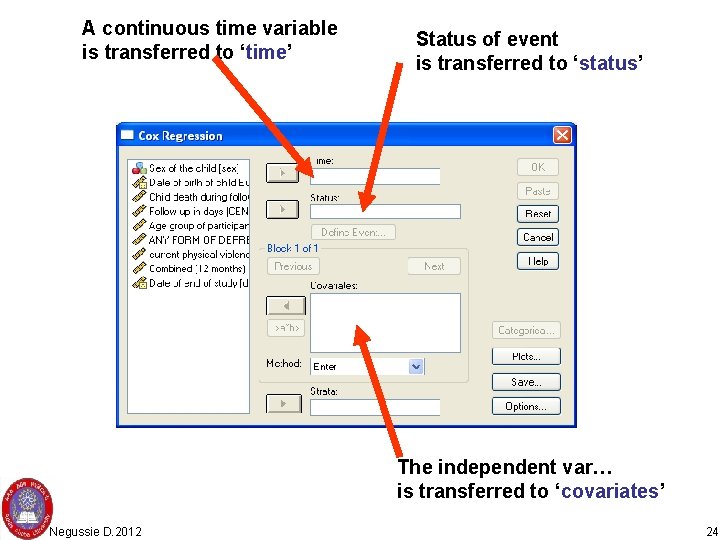
Cox regression Required variables • Time, (duration in days, weeks or month) from date of starting of the follow up until date of the event or outmigration or completing date of the follow up. • A variable describing the study subject’s status on the event (eg death/ alive) • independent variable(s) (categorical or continuous) Negussie D. 2012 23

A continuous time variable is transferred to ‘time’ Status of event is transferred to ‘status’ The independent var… is transferred to ‘covariates’ Negussie D. 2012 24

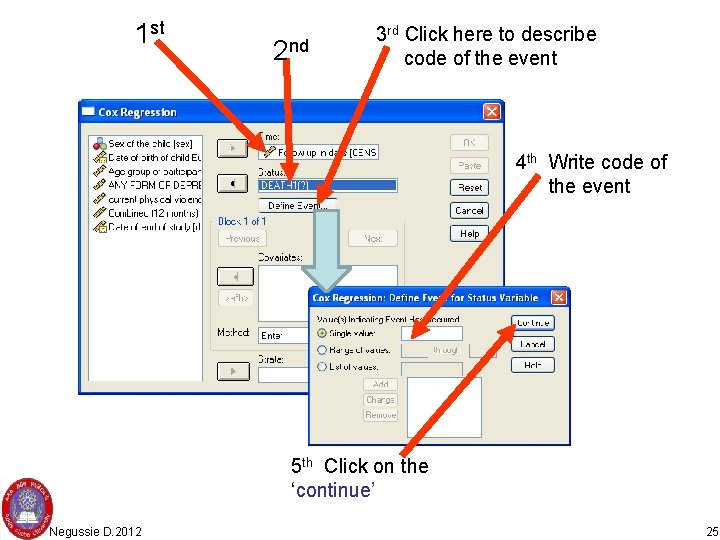
1 st 2 nd 3 rd Click here to describe code of the event 4 th Write code of the event 5 th Click on the ‘continue’ Negussie D. 2012 25

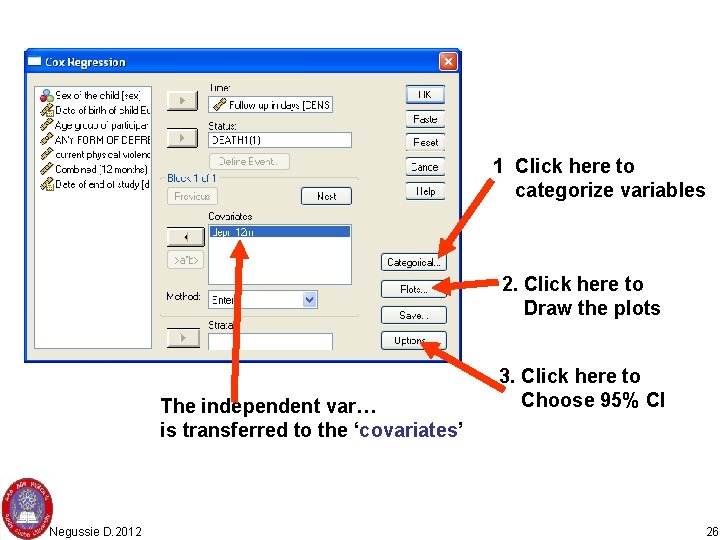
1 Click here to categorize variables 2. Click here to Draw the plots The independent var… is transferred to the ‘covariates’ Negussie D. 2012 3. Click here to Choose 95% CI 26

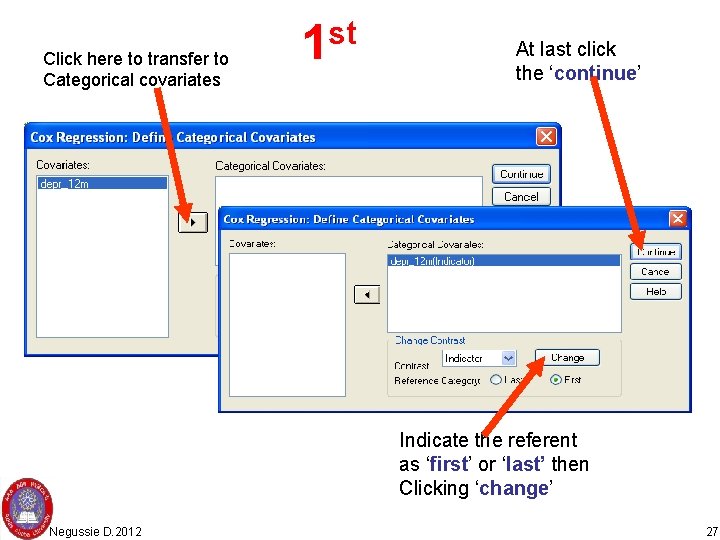
Click here to transfer to Categorical covariates 1 st At last click the ‘continue’ Indicate the referent as ‘first’ or ‘last’ then Clicking ‘change’ Negussie D. 2012 27

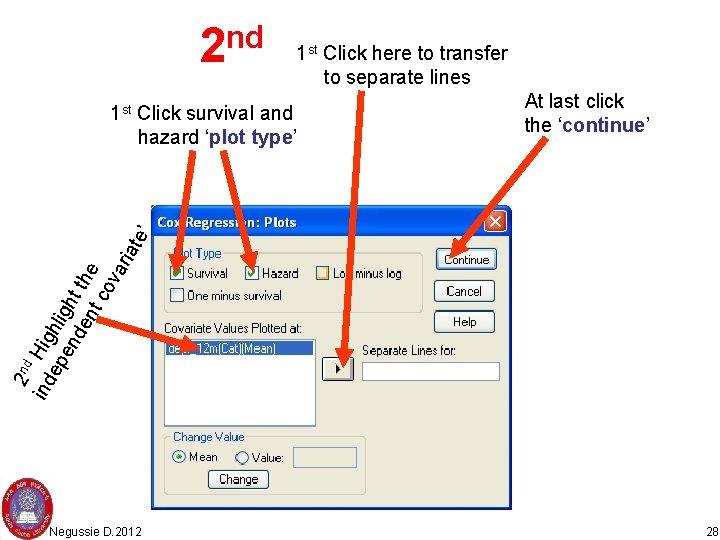
nd 2 1 st Click here to transfer to separate lines At last click the ‘continue’ 2 nd ind Hig ep hlig en de ht th nt e co va ri ate ’ 1 st Click survival and hazard ‘plot type’ Negussie D. 2012 28

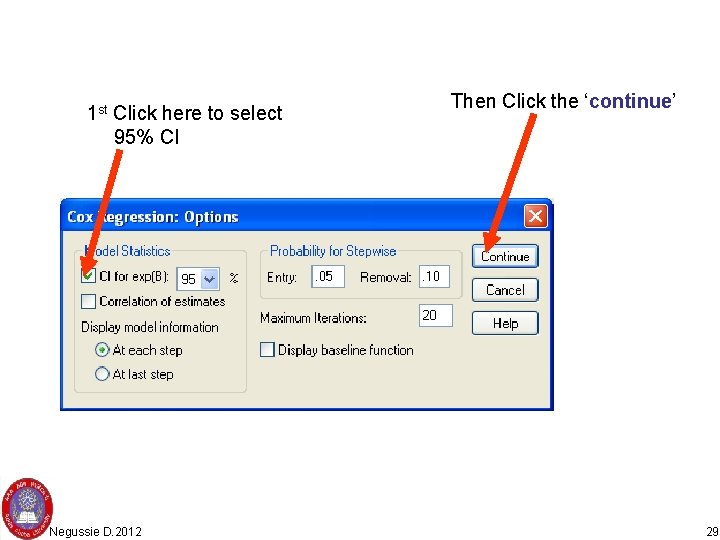
1 st Click here to select 95% CI Negussie D. 2012 Then Click the ‘continue’ 29

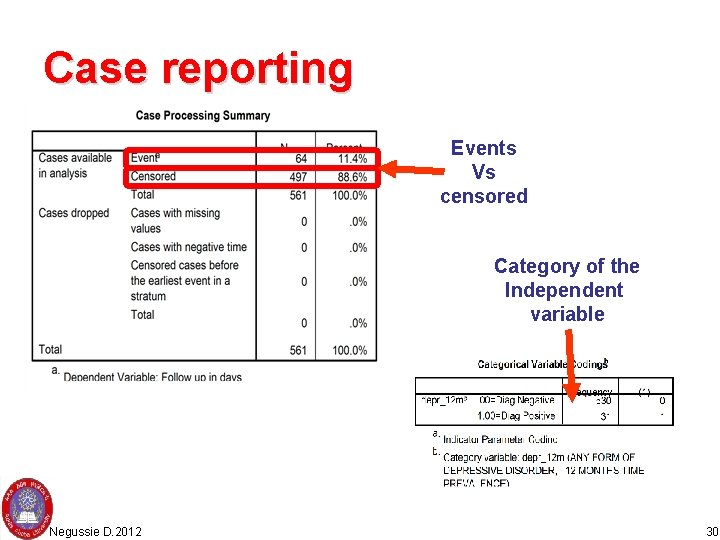
Case reporting Events Vs censored Category of the Independent variable Negussie D. 2012 30

Hazard Ratio (and its 9% CI) Negussie D. 2012 31

Survival function Negussie D. 2012 32

Hazard function Negussie D. 2012 33