Analysis of Variance Schaums Outline Probability and Statistics

Analysis of Variance Schaum’s Outline Probability and Statistics Chapter 9 Examples by Steve Brochu Mark Thomas 1

2 Outline Chapter 9 t test versus F test Analysis of variance Test differences of means across groups Variation within groups Variation between groups Consider (Variation between)/ (Variation within) Explanatory Power of Regression (Variation explained/Variation unexplained)

3 Analysis of Variance – F test t tests inferences on one parameter unknown variances, small sample F tests Analysis of variance difference of means often groups > 2 across models Do variables in regression model explain y Which model is better

4 Analysis of Variance – F test Uranium Mines j different sized mines do costs differ for the j different sized mines (j = 1, . . . , a a=3) 1 = small 2 = medium 3 = large sample 15 mines, 5 (k) in each category sample k mines in each category k = 1, 5 Cost per ton 44 = + ejk ei ~ N(0, 2)

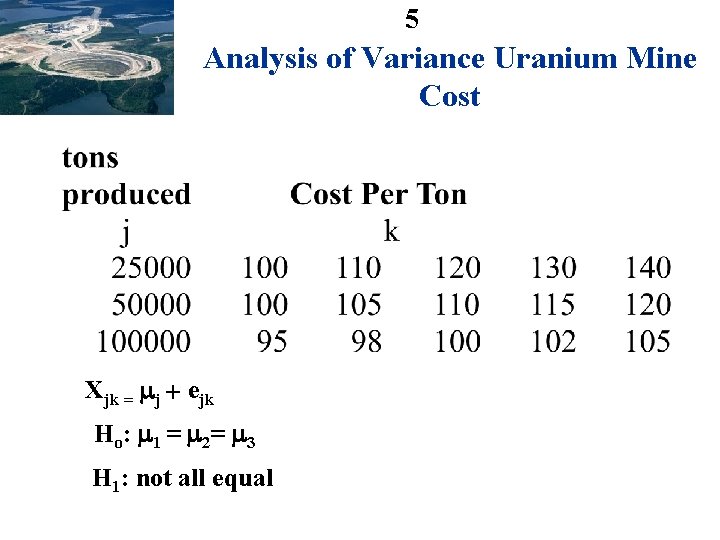
5 Analysis of Variance Uranium Mine Cost Xjk = j + ejk Ho: 1 = 2= 3 H 1: not all equal

6 Variation Within Groups Vw = jk(Xjk- Xj. )2 tons produced j Cost Per Ton (k) 25000 110 120 50000 105 110 100000 95 98 100 Within group variation (100 -120)2 ( ) 0 (100 -110)2 25 0 ( 95 - 100)2 4 0 130 115 102 xj. = 5 k=1 xkj 140 120 110 105 100 400 25 100 4 25 Vw = 1308

7 Distribution of Variation Within Groups (Xjk- j)2/ 2 ~ 21 jk(Xjk- j)2~ 2 T = 2 ab Vw = jk(Xjk- Xj. )2/ 2 = 2 T-a = 2 ab-a

8 Variation Between Groups Vb = jk (Xj. - X)2 =b j (Xj. - X)2 tons produced j Cost Per Ton (k) 25000 110 120 130 50000 105 110 115 100000 95 98 100 102 5(100 -110)2 + (110 -110)2 + ( Xj. 140 120 110 105 100 x 110 )2 = 1000

9 Distribution of Variation Between Groups Total Variation V = jk(Xjk- X)2 = jk(Xjk- Xj. )2 + jk(Xj. - X)2 Vw + Vb V = jk(Xjk- X)2 = jk(Xjk- Xj. )2 + jk(Xj. - X)2 2 If all s the same then T-1 = T-a + ? ? ~ T-1 - T-a = T-1 -(T-a) = a-1 Vb/ 2~ a-1

10 AOV Hypothesis Tests 2 df 1 ~ Fdf 1, df 2 2 df 2 Under null hypothesis Ho: 1 = 2= 3 H 1: not all equal Vb/(a-1) = ŝb 2 = Vw/(ab-a) ŝ w 2 Critical F 2, 12 = 3. 89 500/(3 -1) 1308/(15 -3) = 4. 587

11 AOV with Unequal Number of Observations Vb = jk (Xj. - X)2 = jnj (Xj. - X)2 Vw = jk(Xjk- Xj. )2 Fa-1, T-a = vb/a-1 vw/T-a

12 Fit of Whole Regression y = 1 + 2 x 2 + 3 x 3 +. . . kxk + e R 2 = 1 – êi 2 / y'i 2 = ( ŷ - x)2 + êi 2 Ho: 2 = 3 =. . . = k = 0 H 1: 2, 3, , . . k not all equal to zero Total SS = Explained SS + Error SS Under null hypothesis Total SS/ 2 ~ T-1

13 Fit of Whole Regression Explained SS = Total SS - Error SS 2 2 2 ~ ~ Under null T-1 T-K Explained SS ~ T-1 -(T-K) = K-1 2 Under null Explained SS/ 2 K-1 ~ FK-1, T-K Error SS/ 2 T-K

14 Fit of Whole Regression Under null Explained SS/ 2 K-1 Error SS/ 2 T-K ~ FK-1, T-K

15 9 -155 Analysis of Variance – Summary Differences between t and F testing Analysis of Variance (ANOVA) Tests for equivalence of multiple means (μ 1 = μ 2 …) Utilizes identity that: Total SS = Explained SS + Error SS Compares variation between groups to variation within groups using F test Test statistic is: Need Modification if unequal observations each group