Analysis of torsional splitting in the 8 band

Analysis of torsional splitting in the ν 8 band of propane near 870. 4 cm-1 caused by Fermi resonance with the 2ν 14+2ν 27 level P. Groner Department of Chemistry, University of Missouri - Kansas City, MO, USA A. Perrin, F. Kwabia Tchana LISA, CNRS, Universités Paris Est Créteil et Paris Diderot, Créteil, France L. Manceron CNRS-MONARIS UMR 8233 and Beamline AILES, Synchrotron Soleil, Saint Aubin, France International Symposium on Molecular Spectroscopy, June 20 -24, 2016 1

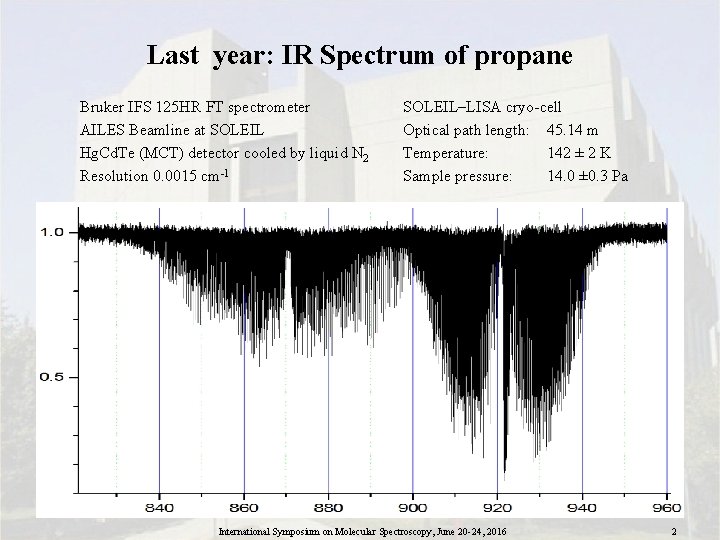
Last year: IR Spectrum of propane Bruker IFS 125 HR FT spectrometer AILES Beamline at SOLEIL Hg. Cd. Te (MCT) detector cooled by liquid N 2 Resolution 0. 0015 cm-1 SOLEIL–LISA cryo-cell Optical path length: 45. 14 m Temperature: 142 ± 2 K Sample pressure: 14. 0 ± 0. 3 Pa International Symposium on Molecular Spectroscopy, June 20 -24, 2016 2

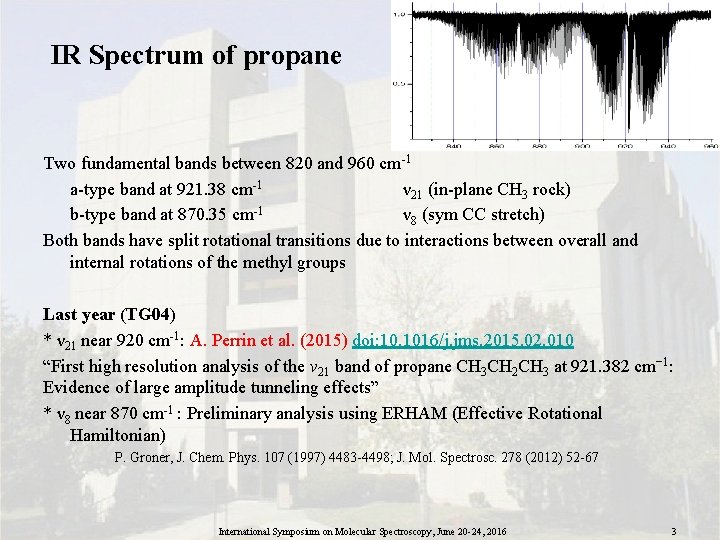
IR Spectrum of propane Two fundamental bands between 820 and 960 cm-1 a-type band at 921. 38 cm-1 ν 21 (in-plane CH 3 rock) b-type band at 870. 35 cm-1 ν 8 (sym CC stretch) Both bands have split rotational transitions due to interactions between overall and internal rotations of the methyl groups Last year (TG 04) * ν 21 near 920 cm-1: A. Perrin et al. (2015) doi: 10. 1016/j. jms. 2015. 02. 010 “First high resolution analysis of the ν 21 band of propane CH 3 CH 2 CH 3 at 921. 382 cm− 1: Evidence of large amplitude tunneling effects” * ν 8 near 870 cm-1 : Preliminary analysis using ERHAM (Effective Rotational Hamiltonian) P. Groner, J. Chem. Phys. 107 (1997) 4483 -4498; J. Mol. Spectrosc. 278 (2012) 52 -67 International Symposium on Molecular Spectroscopy, June 20 -24, 2016 3

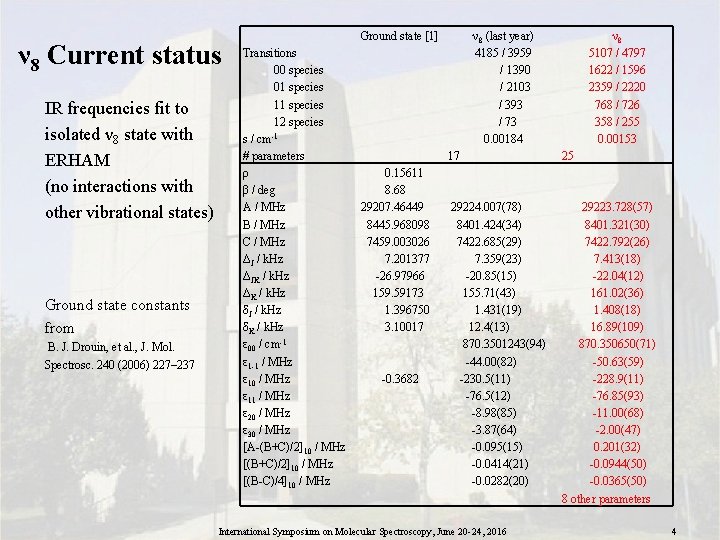
ν 8 Current status IR frequencies fit to isolated ν 8 state with ERHAM (no interactions with other vibrational states) Ground state constants from B. J. Drouin, et al. , J. Mol. Spectrosc. 240 (2006) 227– 237 Ground state [1] Transitions 00 species 01 species 12 species -1 s / cm # parameters ρ β / deg A / MHz B / MHz C / MHz ΔJ / k. Hz ΔJK / k. Hz ΔK / k. Hz δJ / k. Hz δK / k. Hz ε 00 / cm-1 ε 1 -1 / MHz ε 10 / MHz ε 11 / MHz ε 20 / MHz ε 30 / MHz [A-(B+C)/2]10 / MHz [(B-C)/4]10 / MHz 0. 15611 8. 68 29207. 46449 8445. 968098 7459. 003026 7. 201377 -26. 97966 159. 59173 1. 396750 3. 10017 -0. 3682 ν 8 (last year) 4185 / 3959 / 1390 / 2103 / 393 / 73 0. 00184 ν 8 5107 / 4797 1622 / 1596 2359 / 2220 768 / 726 358 / 255 0. 00153 17 25 29224. 007(78) 8401. 424(34) 7422. 685(29) 7. 359(23) -20. 85(15) 155. 71(43) 1. 431(19) 12. 4(13) 870. 3501243(94) -44. 00(82) -230. 5(11) -76. 5(12) -8. 98(85) -3. 87(64) -0. 095(15) -0. 0414(21) -0. 0282(20) 29223. 728(57) 8401. 321(30) 7422. 792(26) 7. 413(18) -22. 04(12) 161. 02(36) 1. 408(18) 16. 89(109) 870. 350650(71) -50. 63(59) -228. 9(11) -76. 85(93) -11. 00(68) -2. 00(47) 0. 201(32) -0. 0944(50) -0. 0365(50) 8 other parameters International Symposium on Molecular Spectroscopy, June 20 -24, 2016 4

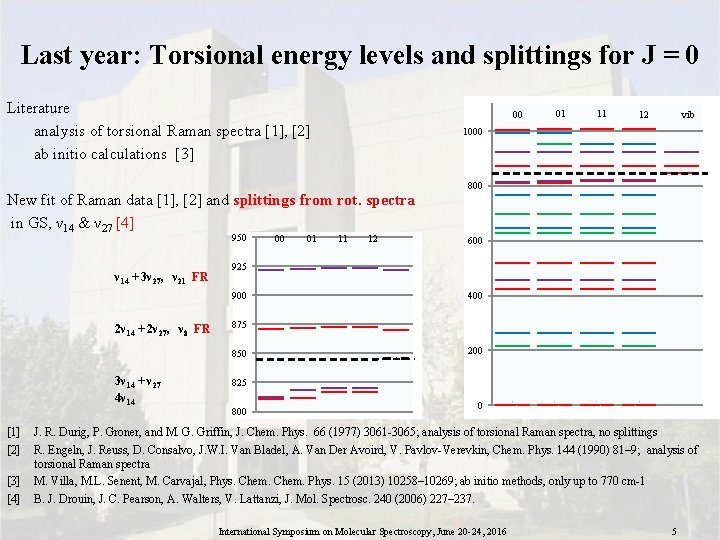
Last year: Torsional energy levels and splittings for J = 0 Literature analysis of torsional Raman spectra [1], [2] ab initio calculations [3] 00 ν 14 + 3ν 27, ν 21 FR [1] [2] [3] [4] vib 11 12 800 600 400 875 850 3ν 14 + ν 27 4ν 14 01 12 925 900 2ν 14 + 2ν 27, ν 8 FR 00 11 1000 New fit of Raman data [1], [2] and splittings from rot. spectra in GS, ν 14 & ν 27 [4] 950 01 200 825 800 0 J. R. Durig, P. Groner, and M. G. Griffin, J. Chem. Phys. 66 (1977) 3061 -3065; analysis of torsional Raman spectra, no splittings R. Engeln, J. Reuss, D. Consalvo, J. W. I. Van Bladel, A. Van Der Avoird, V. Pavlov-Verevkin, Chem. Phys. 144 (1990) 81– 9; analysis of torsional Raman spectra M. Villa, M. L. Senent, M. Carvajal, Phys. Chem. Phys. 15 (2013) 10258– 10269; ab initio methods, only up to 770 cm-1 B. J. Drouin, J. C. Pearson, A. Walters, V. Lattanzi, J. Mol. Spectrosc. 240 (2006) 227– 237. International Symposium on Molecular Spectroscopy, June 20 -24, 2016 5

Perturbations 1 * Fermi resonance possible between ν 8 and 2ν 14 + 2ν 27, both levels have A 1 symmetry * Local resonances observed for some torsional substates, particularly for 01 (EE) International Symposium on Molecular Spectroscopy, June 20 -24, 2016 6

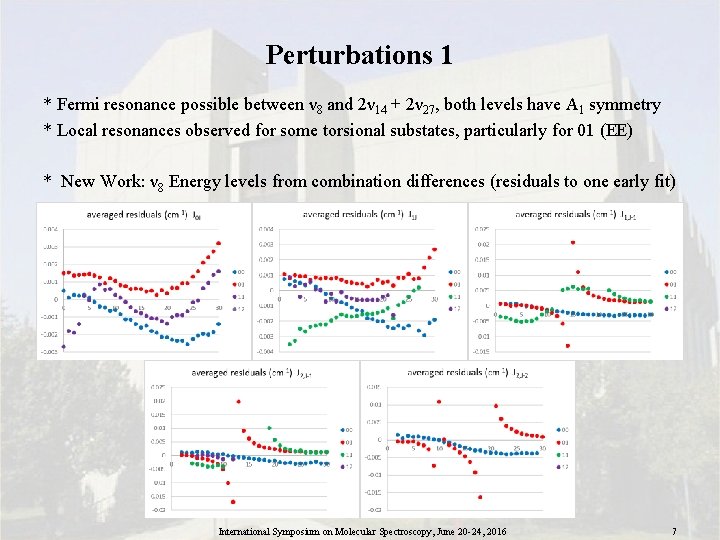
Perturbations 1 * Fermi resonance possible between ν 8 and 2ν 14 + 2ν 27, both levels have A 1 symmetry * Local resonances observed for some torsional substates, particularly for 01 (EE) * New Work: ν 8 Energy levels from combination differences (residuals to one early fit) International Symposium on Molecular Spectroscopy, June 20 -24, 2016 7

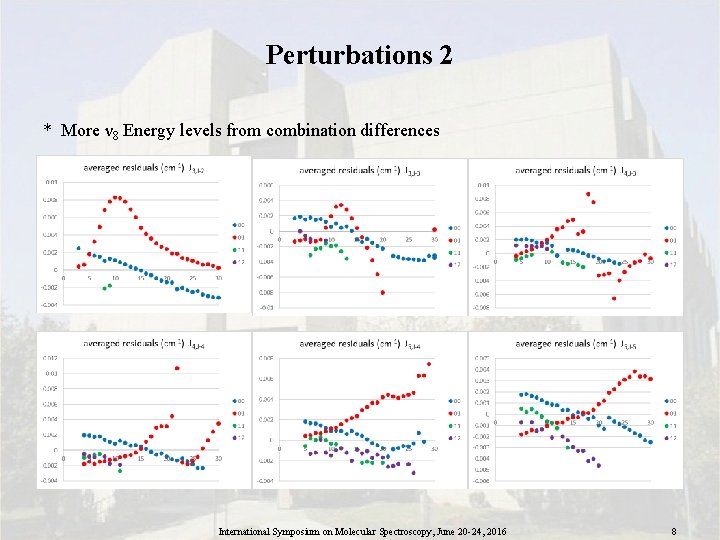
Perturbations 2 * More ν 8 Energy levels from combination differences International Symposium on Molecular Spectroscopy, June 20 -24, 2016 8

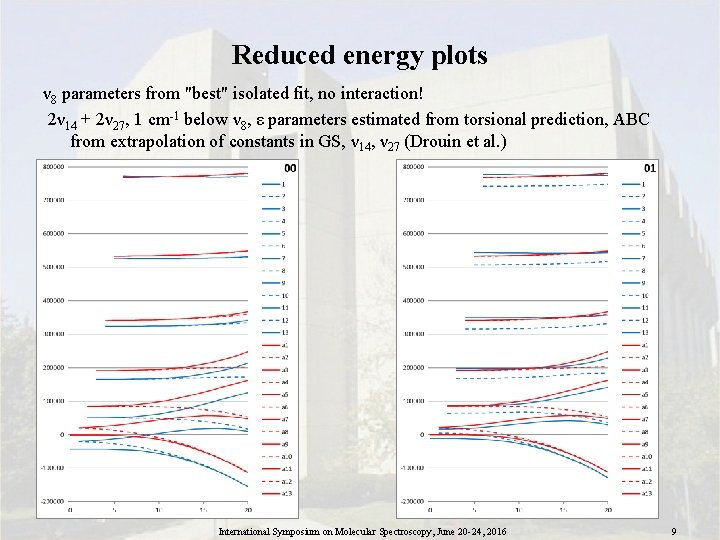
Reduced energy plots ν 8 parameters from "best" isolated fit, no interaction! 2ν 14 + 2ν 27, 1 cm-1 below ν 8, ε parameters estimated from torsional prediction, ABC from extrapolation of constants in GS, ν 14, ν 27 (Drouin et al. ) International Symposium on Molecular Spectroscopy, June 20 -24, 2016 9

Modifications to ERHAM First trials with ERHAM modified to treat Fermi resonance and Coriolis interactions were not successful * Original labeling scheme did not work sufficiently well with interacting states * Reorganize labeling code making full use of molecular symmetry * Generate new input file according to new labeling scheme Test calculations Plots of ν' - ν 0, where Key for interactions. F ν' = calculated frequency with interaction ν 0 = calculated frequency without interaction Fermi term Px, Py, Pz regular Coriolis term Pxt, Pyt, Pzt tunneling Coriolis term International Symposium on Molecular Spectroscopy, June 20 -24, 2016 10

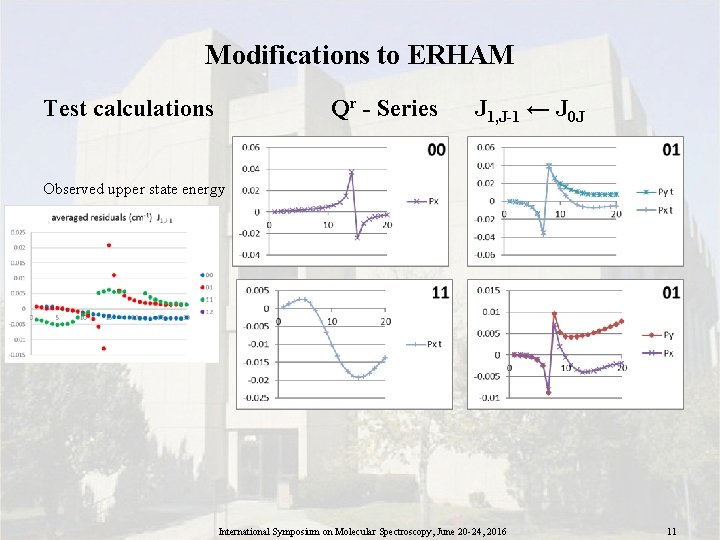
Modifications to ERHAM Test calculations Qr - Series J 1, J-1 ← J 0 J Observed upper state energy International Symposium on Molecular Spectroscopy, June 20 -24, 2016 11

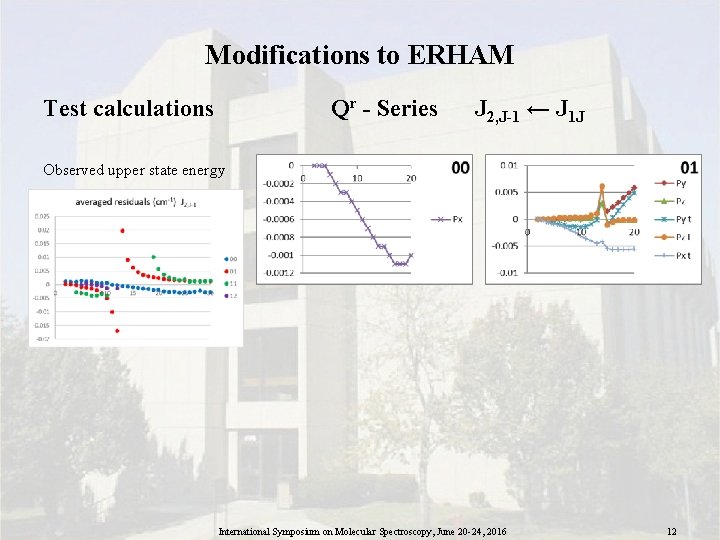
Modifications to ERHAM Test calculations Qr - Series J 2, J-1 ← J 1 J Observed upper state energy International Symposium on Molecular Spectroscopy, June 20 -24, 2016 12

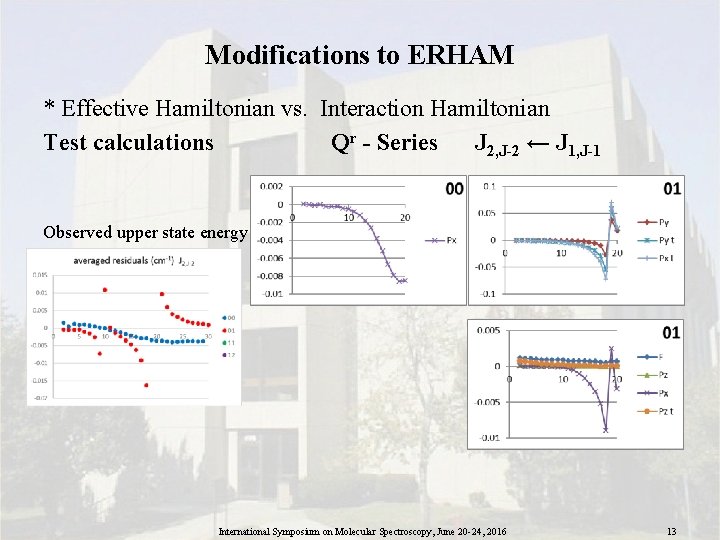
Modifications to ERHAM * Effective Hamiltonian vs. Interaction Hamiltonian Test calculations Qr - Series J 2, J-2 ← J 1, J-1 Observed upper state energy International Symposium on Molecular Spectroscopy, June 20 -24, 2016 13

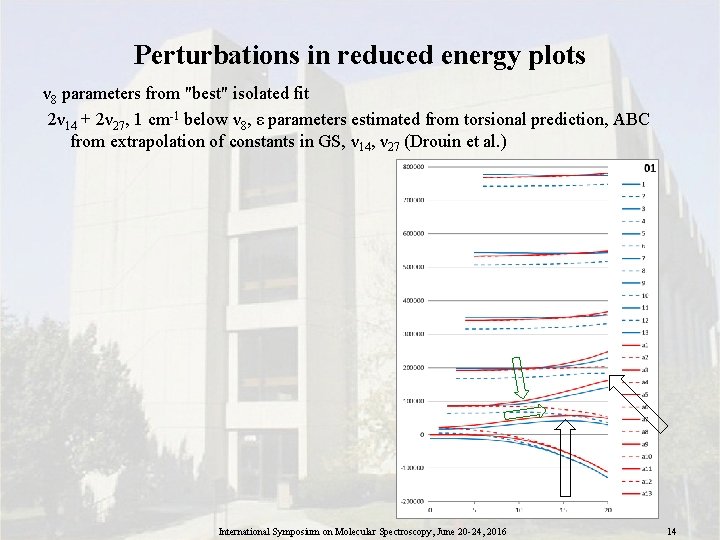
Perturbations in reduced energy plots ν 8 parameters from "best" isolated fit 2ν 14 + 2ν 27, 1 cm-1 below ν 8, ε parameters estimated from torsional prediction, ABC from extrapolation of constants in GS, ν 14, ν 27 (Drouin et al. ) International Symposium on Molecular Spectroscopy, June 20 -24, 2016 14

Effective rotational Hamiltonian (isolated vibrational state) or The expressions for Sl and S 0 depend on the exact symmetry of the problem. International Symposium on Molecular Spectroscopy, June 20 -24, 2016 15

Interacting states * and The coefficients Tlqq' and T'lqq' are in this version the sums or differences of the original coefficients Tlv'v, q, q' and Tlv'v, -q-, q'. Luckily, program did not have to be changed except for one little test Insufficient time to try this out. International Symposium on Molecular Spectroscopy, June 20 -24, 2016 16

Where are we now? (Conclusions) * The LS fit still is elusive (shots-into-the-dark trials have not worked) * We don’t know Of the perturbing dark state Identity, energy, A, B, C, tunneling coefficients / splittings Of the interaction operators Kinds and magnitudes Based on experimental results, some (like Px) can be ruled out * Other potential perturber: ν 9 + 2ν 27 (A 1) about 20 cm-1 higher (does not solve the problem of identifying the dark state) International Symposium on Molecular Spectroscopy, June 20 -24, 2016 17

Thank you International Symposium on Molecular Spectroscopy, June 20 -24, 2016 18