Analysis of Sorting Algorithms 1 Examples n n



















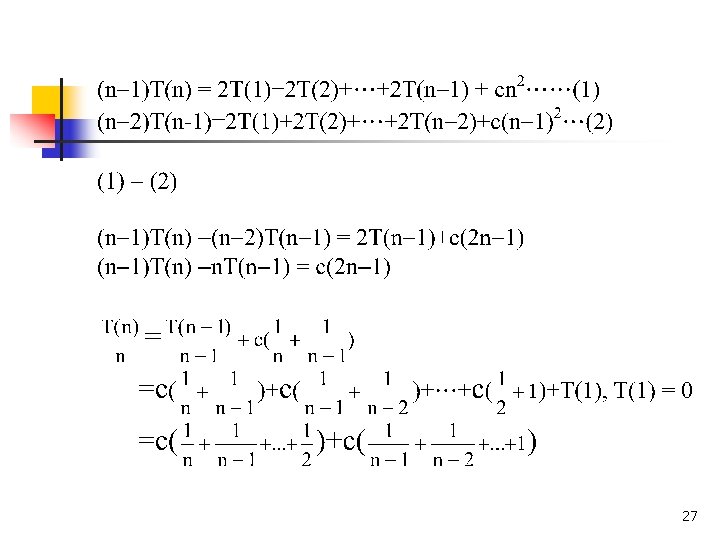



![The Merge Procedure Merge(A, p, q, r) ● Copy A[p. . q] and A[q The Merge Procedure Merge(A, p, q, r) ● Copy A[p. . q] and A[q](https://slidetodoc.com/presentation_image_h/2d02ddbe6e1189f219864bb140cdd919/image-32.jpg)



- Slides: 36

Analysis of Sorting Algorithms 1

Examples n n Bubble Sort Insertion Sort Quick Sort Merge Sort 2




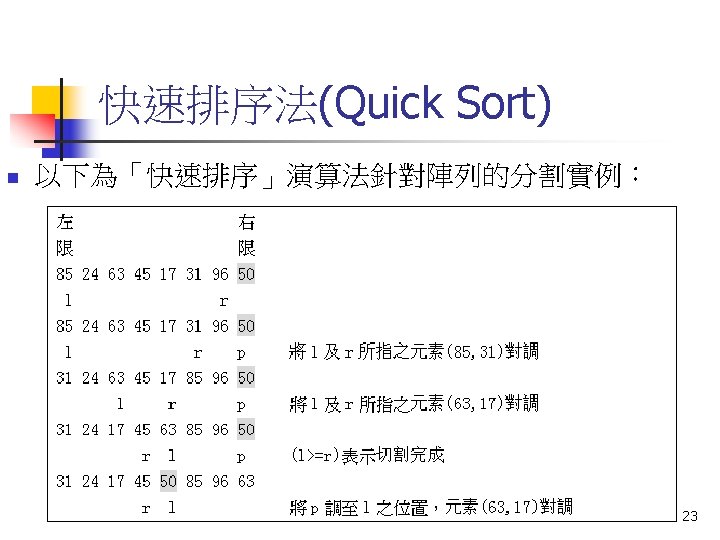
氣泡排序(Bubble Sort)(4/7) 6

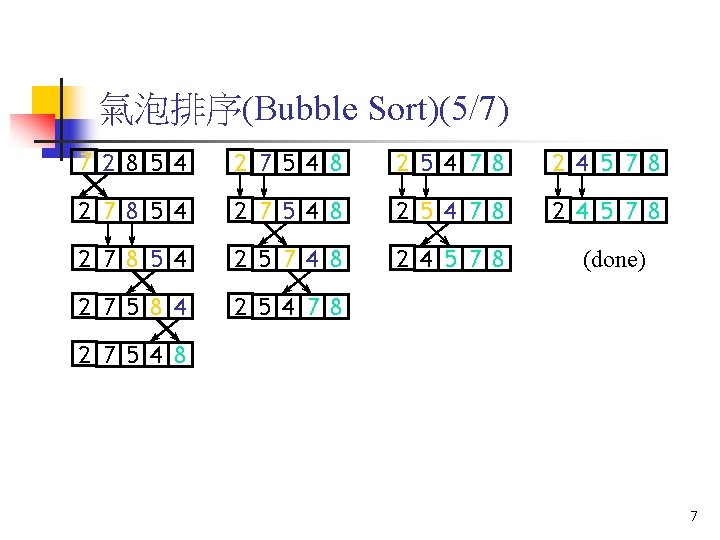
氣泡排序(Bubble Sort)(5/7) 7 2 8 5 4 2 7 5 4 8 2 5 4 7 8 2 4 5 7 8 2 7 8 5 4 2 5 7 4 8 2 4 5 7 8 2 7 5 8 4 2 5 4 7 8 (done) 2 7 5 4 8 7










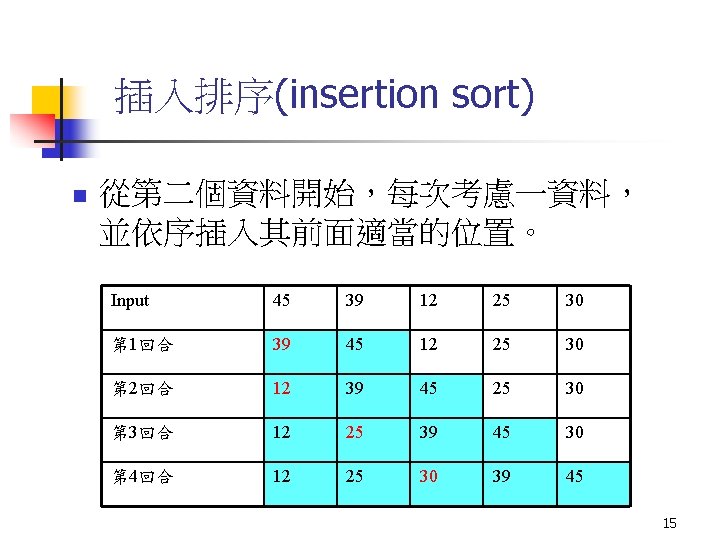
Straight insertion sort input: 7, 5, 1, 4, 3 5, 7, 1, 4, 3 1, 5, 7, 4, 3 1, 4, 5, 7, 3 1, 3, 4, 5, 7 17 Algorithm 2. 1 Straight Insertion Sort Input: x 1, x 2, . . . , xn Output: The sorted sequence of x 1, x 2, . . . , xn For j : = 2 to n do Begin i : = j-1 x : = xj While x<xi and i > 0 do Begin xi+1 : = xi i : = i-1 End xi+1 : = x End

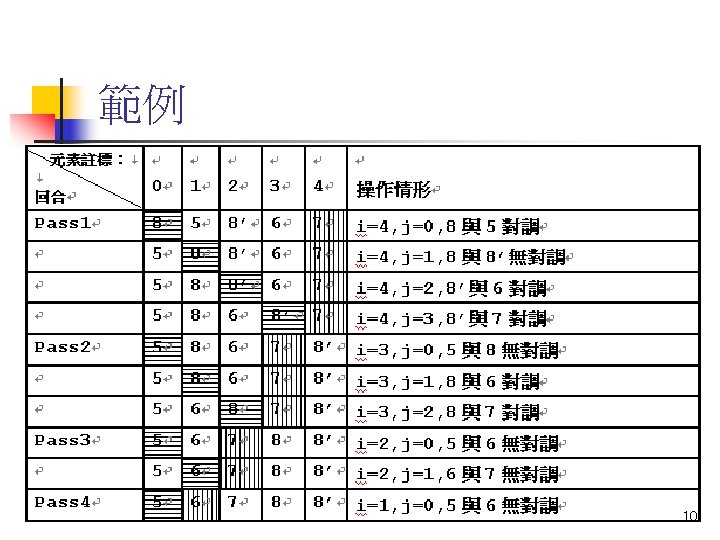
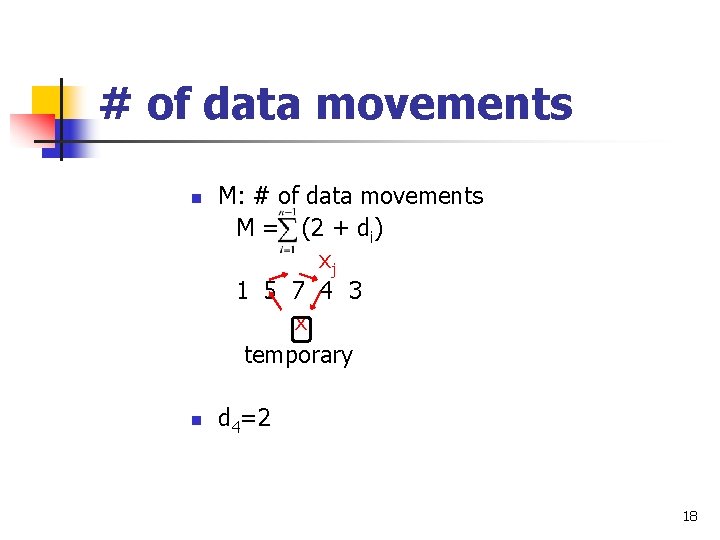
# of data movements M: # of data movements M = (2 + di) xj 1 5 7 4 3 x temporary n n d 4=2 18

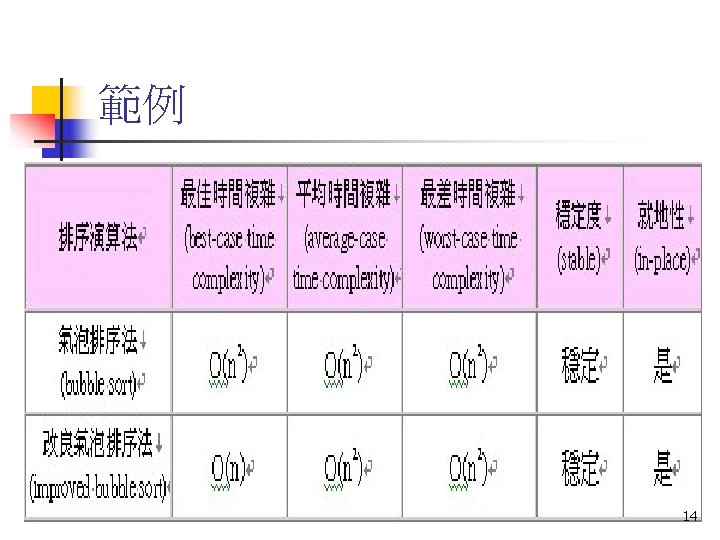
Analysis of Insertion Sort best case: already sorted n di = 0 for 1 i n M = 2(n 1) = O(n) n n worst case: reversely sorted d 1 = n 1 d 2 = n 2 n : di = n i 1 4 7 5 : n dn = 0 di = (n i) i=0, n-1 di=n(n-1)/2 n M = n(n 1)/2+2(n 1) = O(n 2) n average case: xj is being inserted into the sorted sequence x 1 x 2. . . xj-1 the probability that xj is the largest: 1/j n takes 2 data movements the probability that xj is the second largest : 1/j n takes 3 data movements : # of movements for xj to be inserted: 2/j+3/j+. . . +(j+1)/j=(j+3)/2 M= j=2, n(j+3)/2= (n+8)(n 1)/4 = O(n 2) 19





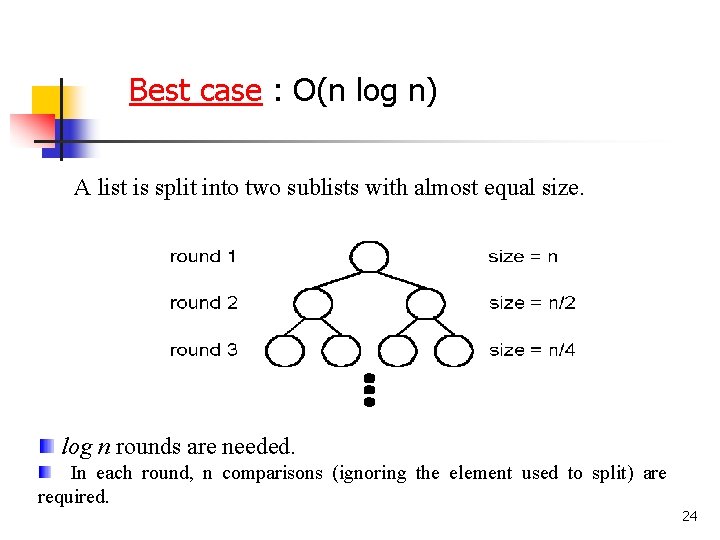
Best case : O(n log n) A list is split into two sublists with almost equal size. log n rounds are needed. In each round, n comparisons (ignoring the element used to split) are required. 24

Worst case : O(n 2) In each round, the number used to split is either the smallest or the largest. 25

Average case: O(n log n) 26
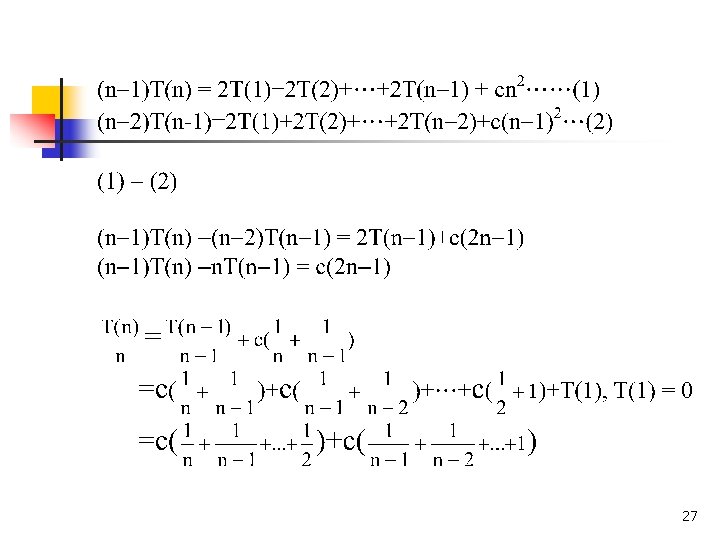
27

28



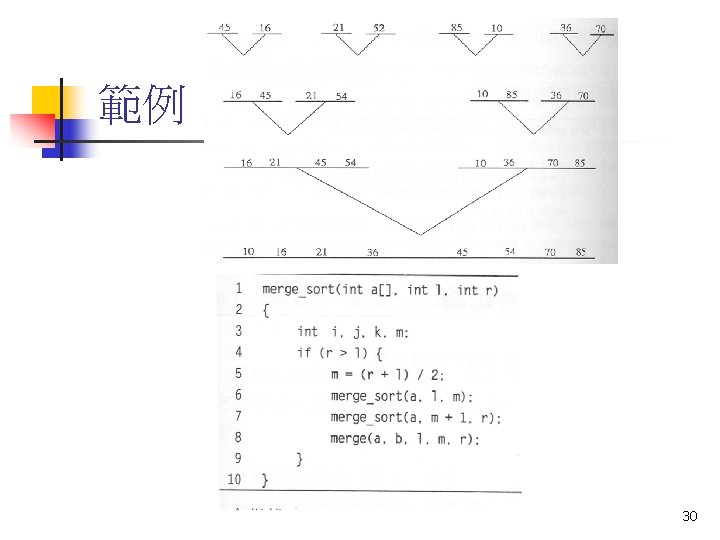
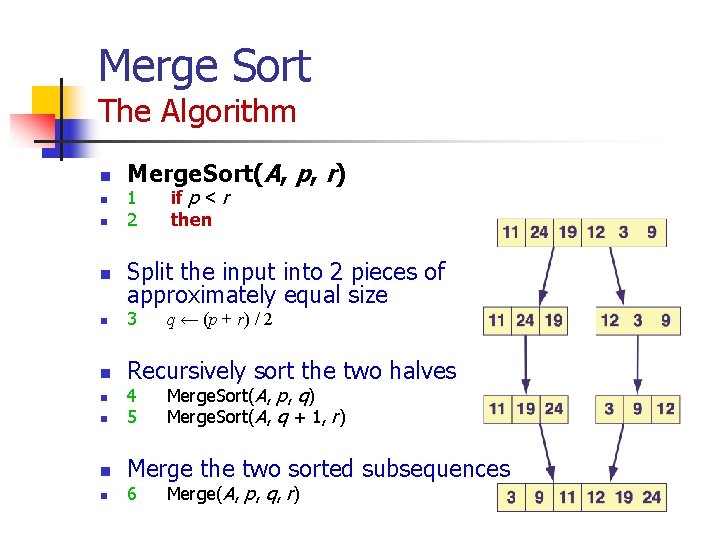
Merge Sort The Idea If |A| = 1, the data is already sorted; done. Otherwise: Split the input into two pieces of equal size. Recursively sort these two pieces. Construct a sorted sequence from the two sorted subsequences.
![The Merge Procedure MergeA p q r Copy Ap q and Aq The Merge Procedure Merge(A, p, q, r) ● Copy A[p. . q] and A[q](https://slidetodoc.com/presentation_image_h/2d02ddbe6e1189f219864bb140cdd919/image-32.jpg)
The Merge Procedure Merge(A, p, q, r) ● Copy A[p. . q] and A[q + 1. . r] to temporary arrays L and R: 1 2 3 4 5 6 n 1 ← q – p + r n 2 ← r – q for i = 1. . n 1 do L[i] ← A[p + i – 1] for j = 1. . n 2 do R[j] ← A[q + j] ● Create two artificial end markers that are never copied to A: 7 L[n 1 + 1] ← ∞ 8 R[n 2 + 1] ← ∞ ● Repeatedly copy the smallest element from L and R to A: 9 i ← 1 10 j ← 1 11 for k = p. . r 12 do if L[i] ≤ R[j] 13 then A[k] ← L[i] 14 i ← i + 1 15 else A[k] ← R[j] 16 j ← j + 1

Merge Sort The Algorithm n n Merge. Sort(A, p, r) 1 2 if p < r then Split the input into 2 pieces of approximately equal size n 3 n Recursively sort the two halves q ← (p + r) / 2 Merge. Sort(A, p, q) Merge. Sort(A, q + 1, r) n 4 5 n Merge the two sorted subsequences n n 6 Merge(A, p, q, r)

34

Quick Sort n n Quicksort is a sorting algorithm whose worstcase running time is (n 2) on an input array of n numbers. In spite of this slow worst-case running time, quicksort is often the best practical choice for sorting because it is remarkably efficient on the average: its expected running time is O(n long n), and the constant factors hidden in the O(n log n) is quite small. 35

Q&A 36