Analysis of IEEE 802 11 e and Application

Analysis of IEEE 802. 11 e and Application of Game Models for Support of Quality-of-Service in Coexisting Wireless Networks Stefan Mangold Com. Nets Aachen University 30 -June-2003

Outline IEEE 802. 11 wireless LAN Brief introduction: Distributed Coordination Function (DCF) IEEE 802. 11 e Qo. S extension Overview: Enhanced DCF (EDCF) Achievable throughput with the EDCF Model for achievable throughput per priority Result evaluation with WARP 2 Overlapping radio networks in unlicensed bands Game model of competition Result evaluation with You. Shi Analysis of competition scenario: stability, expected outcomes Cooperation in repeated games Conclusions Stefan Mangold - Com. Nets Aachen University 1

Motivation of this Thesis IEEE 802. 11 is the dominant radio system for wireless Local Area Networks (LANs): Today’s Wireless LANs cannot support Quality of Service (Qo. S) However, the demand is growing for new applications with Qo. S requirements Wireless LANs operate in unlicensed frequency bands, where they have to share radio resources Problems/Questions: How to support Qo. S in wireless LANs? If wireless LANs can support Qo. S, what level of Qo. S can be maintained in unlicensed frequency bands? New methods to support Qo. S in wireless LANs are developed and evaluated in this thesis. Stefan Mangold - Com. Nets Aachen University 2

IEEE 802. 11 Wireless LAN Radio standard for data transport system that covers ISO/OSI layer 1 and 2: Multiple Physical (PHY) layers: . 11/. 11 a/. 11 b/. 11 g One common Medium Access Control (MAC) layer Here: IEEE 802. 11 a PHY OFDM multi-carrier transmission Up to 54 Mbit/s (@PHY) 5 GHz unlicensed band Shared resources Main Service: MSDU Delivery Reference model Stefan Mangold - Com. Nets Aachen University 3

Medium Access Distributed Coordination Function (DCF) Listen before talk: CSMA/CA Binary exponential backoff Contention window increases with each retransmission Received MPDUs (data frames) are acknowledged Variable frame body sizes (up to 2312 byte) One queue per station Collisions occur if many stations operate in parallel Stefan Mangold - Com. Nets Aachen University 4

IEEE 802. 11 Wireless LAN Basics MAC protocol is distributed (simple and successful) One queue per station (station = backoff entity) MSDU can be fragmented into multiple MPDUs RTS/CTS helps to improve efficiency Qo. S involves achieving a minimum MSDU Delivery throughput and MSDU Delivery delays not exceeding a maximum limit Delay variation and loss rate are often considered IEEE 802. 11 Task Group E (TGe) defines Qo. S mechanisms to be integrated into the legacy 802. 11 MAC This supplement standard is referred to as IEEE 802. 11 e (here: draft 4. 0) Qo. S Support in legacy 802. 11? no! Stefan Mangold - Com. Nets Aachen University 5

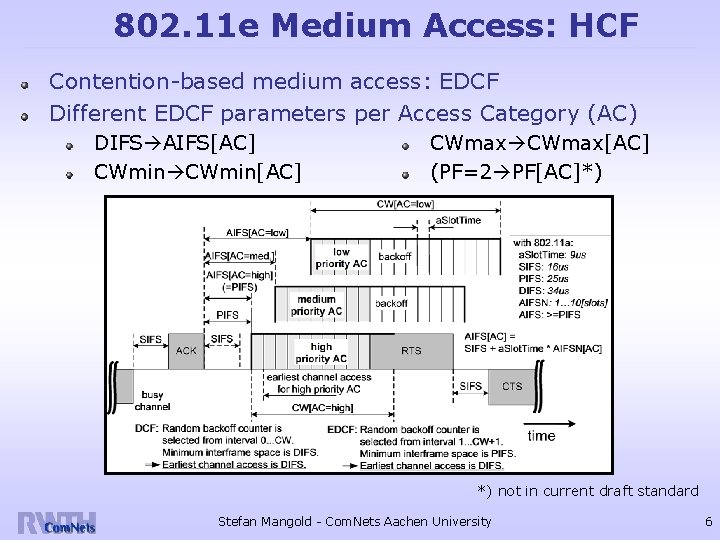
802. 11 e Medium Access: HCF Contention-based medium access: EDCF Different EDCF parameters per Access Category (AC) DIFS AIFS[AC] CWmin[AC] CWmax[AC] (PF=2 PF[AC]*) *) not in current draft standard Stefan Mangold - Com. Nets Aachen University 6

Achievable Throughput Three different EDCF parameter sets AC (priority): higher medium(=legacy) AIFSN[AC]: CWmin[AC]: CWmax[AC]: PF[AC]: 2 7 1023 24/16 2 15 1023 32/16 lower 9 31 1023 40/16 Question: achievable throughput per backoff entity in an isolated scenario? "saturation throughput" Isolated scenario means: the same EDCF parameters are use by all backoff entities Results depend on: frame body length, number of contending backoff entities, RTS/CTS, fragmentation Approach: WARP 2 stochastic simulation and analytical model (modifications of Bianchi’s legacy 802. 11 model) Stefan Mangold - Com. Nets Aachen University 7

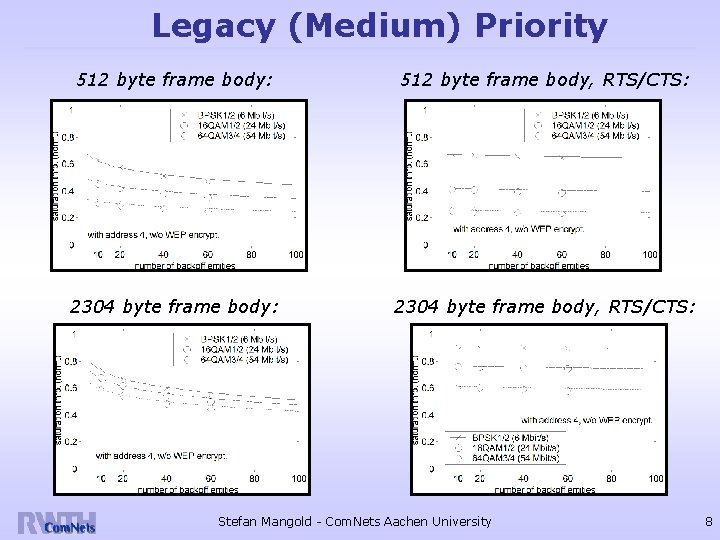
Legacy (Medium) Priority 512 byte frame body: 512 byte frame body, RTS/CTS: 2304 byte frame body, RTS/CTS: Stefan Mangold - Com. Nets Aachen University 8

Low Priority (larger CWmin[AC]) 512 byte frame body: 512 byte frame body, RTS/CTS: 2304 byte frame body, RTS/CTS: Stefan Mangold - Com. Nets Aachen University 9

High Priority (smaller CWmin[AC]) 512 byte frame body: 512 byte frame body, RTS/CTS: 2304 byte frame body, RTS/CTS: Stefan Mangold - Com. Nets Aachen University 10

Modified Bianchi Model Stefan Mangold - Com. Nets Aachen University 11

Share of Capacity Saturation throughput shown so far is only valid for isolated scenarios Nice to have, but useless for Qo. S support: For Qo. S support, a backoff entity needs to know the expected throughput in mixed scenarios Achievable throughput per backoff entity is referred to as "share of capacity" Question: what is the share of capacity a backoff entity can achieve in a mixed scenario? This is *THE* important question for EDCF Qo. S support Bianchi model does not provide the answer There is no solution available until today Stefan Mangold - Com. Nets Aachen University 12

Access Probability per Slot Stefan Mangold - Com. Nets Aachen University 13

Approximation of Expected Idle Times Expected size of contention window N[AC] = number of backoff entities of AC tau[AC] = probability that a backoff entity is transmitting Access probability per slot Expressed by geometric distribution Stefan Mangold - Com. Nets Aachen University 14

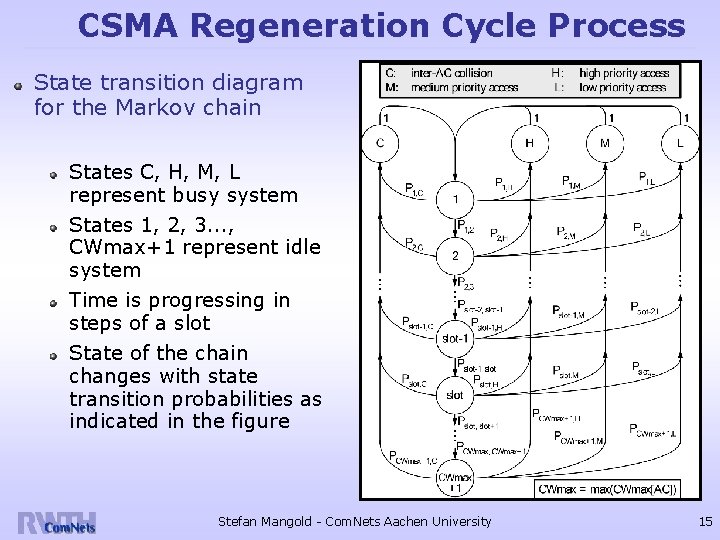
CSMA Regeneration Cycle Process State transition diagram for the Markov chain States C, H, M, L represent busy system States 1, 2, 3. . . , CWmax+1 represent idle system Time is progressing in steps of a slot State of the chain changes with state transition probabilities as indicated in the figure Stefan Mangold - Com. Nets Aachen University 15

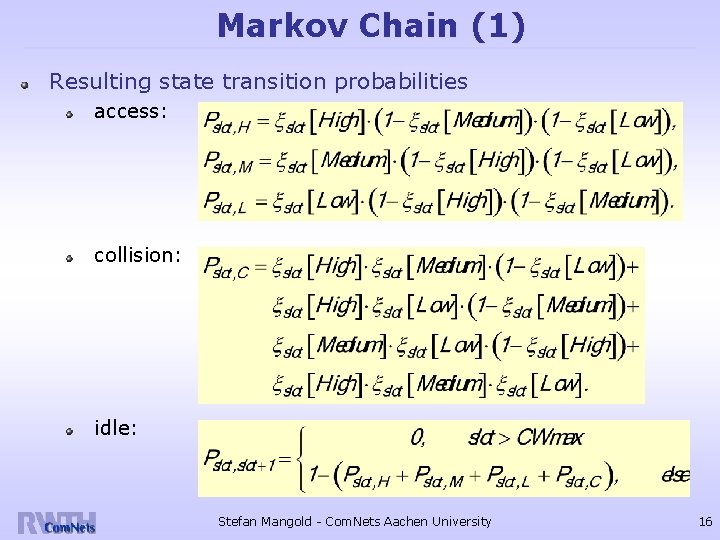
Markov Chain (1) Resulting state transition probabilities access: collision: idle: Stefan Mangold - Com. Nets Aachen University 16

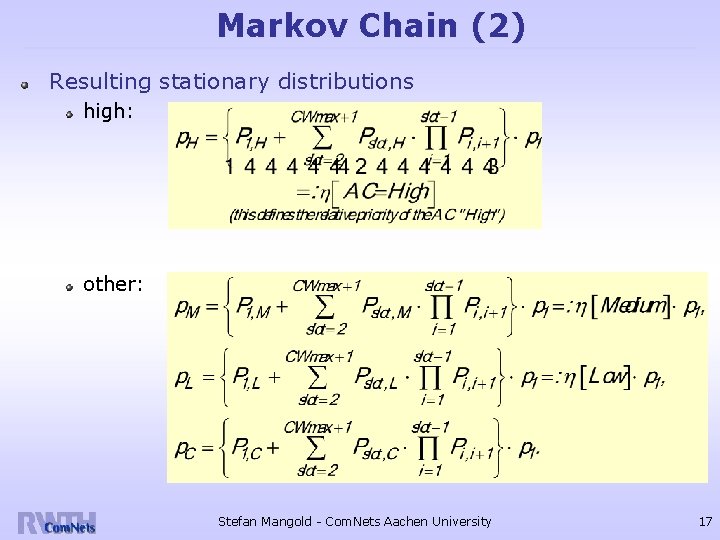
Markov Chain (2) Resulting stationary distributions high: other: Stefan Mangold - Com. Nets Aachen University 17

Result The priority vector Share of capacity Modified Bianchi model provides the saturation throughput Stefan Mangold - Com. Nets Aachen University 18

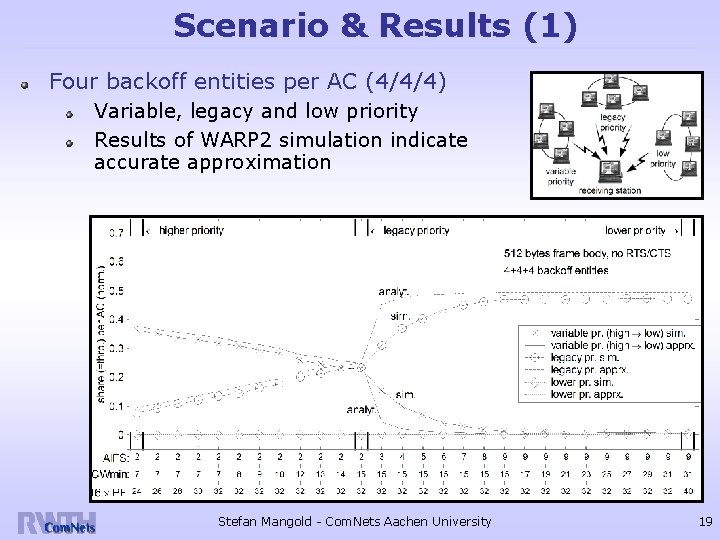
Scenario & Results (1) Four backoff entities per AC (4/4/4) Variable, legacy and low priority Results of WARP 2 simulation indicate accurate approximation Stefan Mangold - Com. Nets Aachen University 19

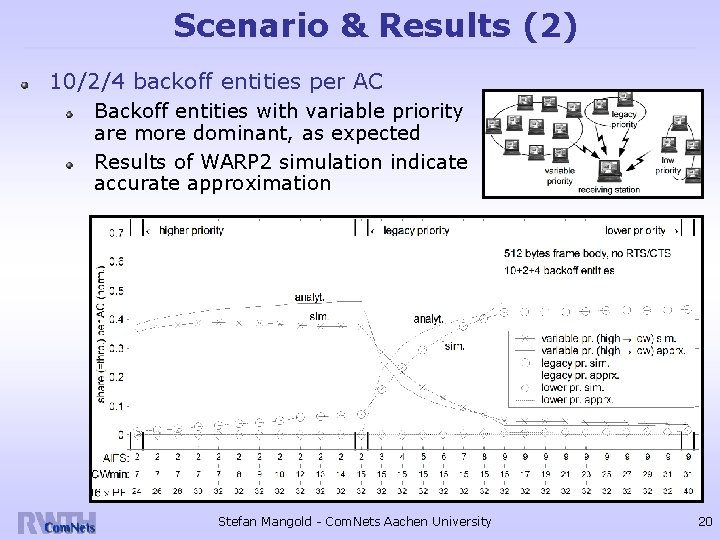
Scenario & Results (2) 10/2/4 backoff entities per AC Backoff entities with variable priority are more dominant, as expected Results of WARP 2 simulation indicate accurate approximation Stefan Mangold - Com. Nets Aachen University 20

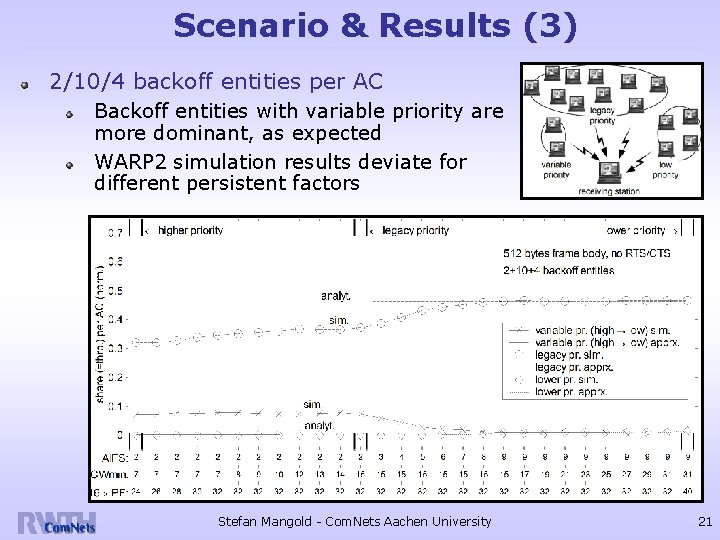
Scenario & Results (3) 2/10/4 backoff entities per AC Backoff entities with variable priority are more dominant, as expected WARP 2 simulation results deviate for different persistent factors Stefan Mangold - Com. Nets Aachen University 21

EDCF Summary EDCF MAC protocol is distributed (as DCF, simple) Multiple queues per station (queue = backoff entity) The presented model can be used for prediction of expected share of capacity per backoff entity The model can be extended towards delay and loss prediction EDCF supports Qo. S, but cannot guarantee as resulting share depends on activity of other backoff entities Qo. S Support in legacy 802. 11? no! Qo. S Support in 802. 11 e EDCF? yes, but no guarantee! Stefan Mangold - Com. Nets Aachen University 22

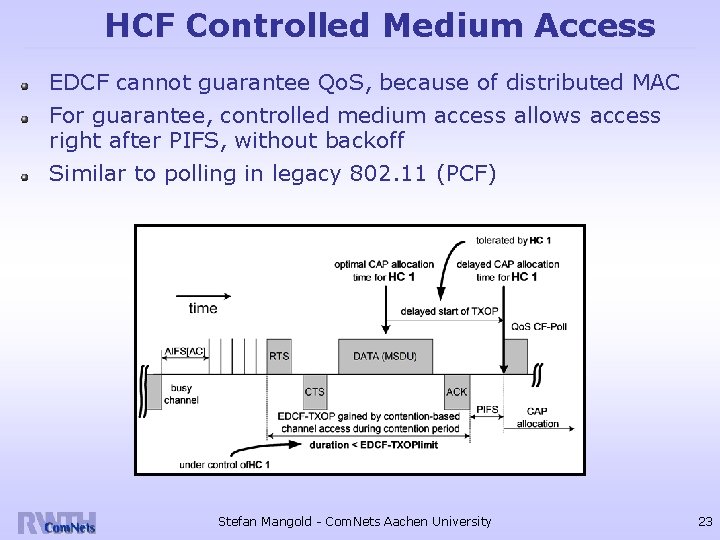
HCF Controlled Medium Access EDCF cannot guarantee Qo. S, because of distributed MAC For guarantee, controlled medium access allows access right after PIFS, without backoff Similar to polling in legacy 802. 11 (PCF) Stefan Mangold - Com. Nets Aachen University 23

HCF in Overlapping BSS Controlled medium access requires an isolated BSS No other backoff entity must access the medium with highest priority (after PIFS), otherwise collisions occur! This is a very strict requirement, and difficult to achieve in an unlicensed frequency band Dynamic frequency selection may help, as in Hiper. LAN/2 512 byte frame body: 2304 byte frame body: Stefan Mangold - Com. Nets Aachen University 24

HCF Controlled Access Summary The controlled medium access is often referred to as HCF This coordination function is not distributed, it is centralized (requires a Hybrid Coordinator) It works only in isolated scenarios, which is not a very likely scenario in unlicensed bands The coexistence problem of overlapping BSSs will be discussed in the following Qo. S Support in legacy 802. 11? no! Qo. S Support in 802. 11 e EDCF? yes, but no guarantee! Qo. S Support with 802. 11 e HCF? not in unlicensed bands! Stefan Mangold - Com. Nets Aachen University 25

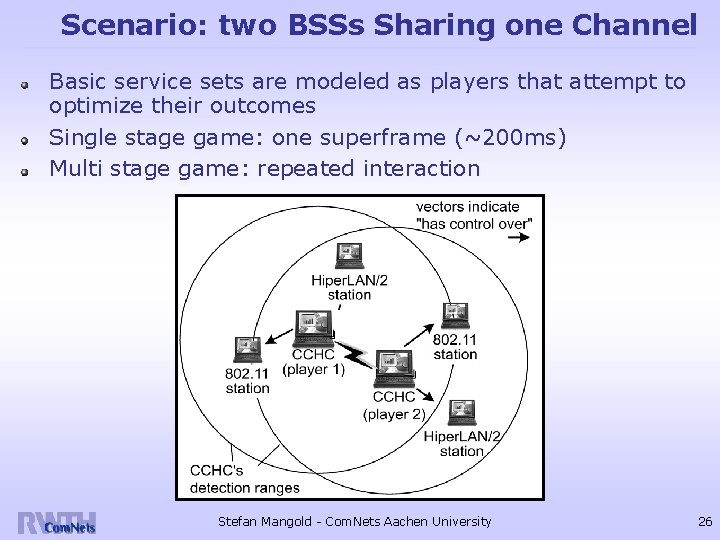
Scenario: two BSSs Sharing one Channel Basic service sets are modeled as players that attempt to optimize their outcomes Single stage game: one superframe (~200 ms) Multi stage game: repeated interaction Stefan Mangold - Com. Nets Aachen University 26

The Superframe as Single Stage Game Allocation process during a superframe: Qo. S: Stefan Mangold - Com. Nets Aachen University 27

Abstract Representation of Qo. S Throughput: normalized share of capacity Delay: normalized resource allocation interval , Jitter: normalized delay variation Stefan Mangold - Com. Nets Aachen University 28

The Player "i" and opponent player "–i" have individual requirements Players select demands to meet requirements Through allocation process, players observe outcomes per single stage game: observed Qo. S This single stage game is repeated with every superframe Players adapt behaviors in the multi stage game Stefan Mangold - Com. Nets Aachen University 29

Allocation Process (Formal Description) Required: If this process can be formally described through an accurate approximation, we can analyze. Expected outcomes (existence of Nash equilibrium (NE)) Stability (convergence to NE) Fairness (position of NE in bargaining domain) It can be discussed… … what Qo. S support is feasible for the individual players (player = CCHC = BSS) … what level of Qo. S can be achieved … if mutual cooperation improves the outcome per player Stefan Mangold - Com. Nets Aachen University 30

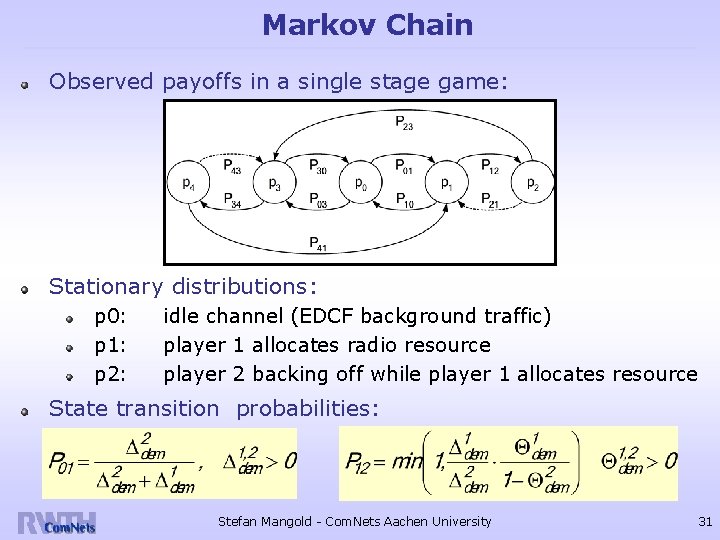
Markov Chain Observed payoffs in a single stage game: Stationary distributions: p 0: p 1: p 2: idle channel (EDCF background traffic) player 1 allocates radio resource player 2 backing off while player 1 allocates resource State transition probabilities: Stefan Mangold - Com. Nets Aachen University 31

Result and Evaluation Resulting observations for both players: Comparison with simulation results (You. Shi): Stefan Mangold - Com. Nets Aachen University 32

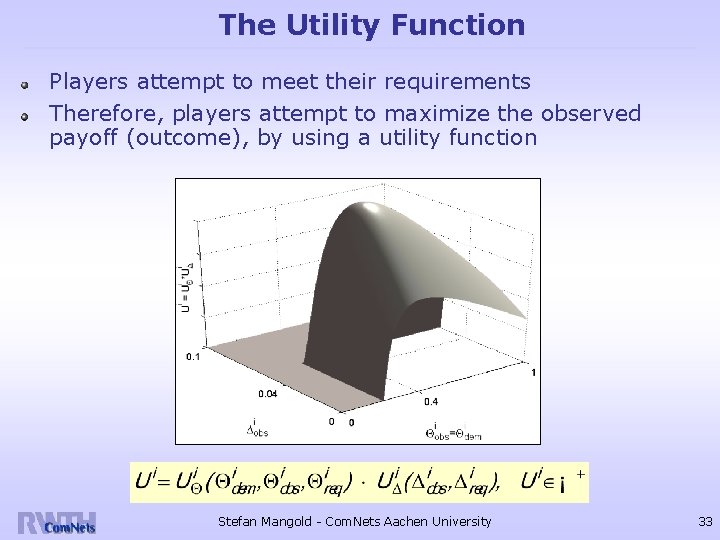
The Utility Function Players attempt to meet their requirements Therefore, players attempt to maximize the observed payoff (outcome), by using a utility function Stefan Mangold - Com. Nets Aachen University 33

Existence of Nash Equilibrium (NE) Proposition: in the Single Stage Game of two coexisting CCHCs exists a Nash equilibrium in the action space A. Proof: show that the outcome (the payoff V) is continuous in A, and show that it is quasi-concave in Ai. There exists at least one Nash equilibrium, which can be calculated as: a=action, V=payoff, N=number of players (N=2) Stefan Mangold - Com. Nets Aachen University 34

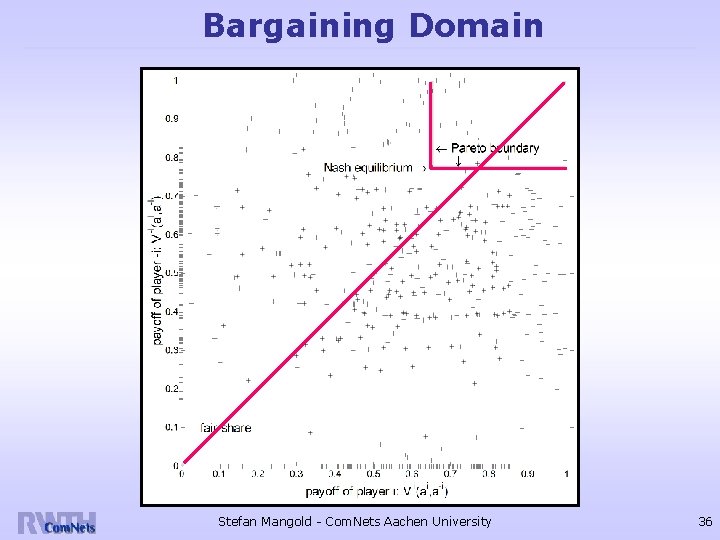
Pareto Efficiency Players that take rational actions will automatically adjust into a NE (because there is at least one NE) If the NE is unique, the respective action profile can be predicted as expected point of operation However, there may exist action profiles in the single stage game that lead to higher payoffs If such profiles do not exist, the NE is referred to as Pareto efficient (Pareto optimal) Pareto efficiency can be determined by numerical search Can be shown in bargaining domain … (next page) Stefan Mangold - Com. Nets Aachen University 35

Bargaining Domain Stefan Mangold - Com. Nets Aachen University 36

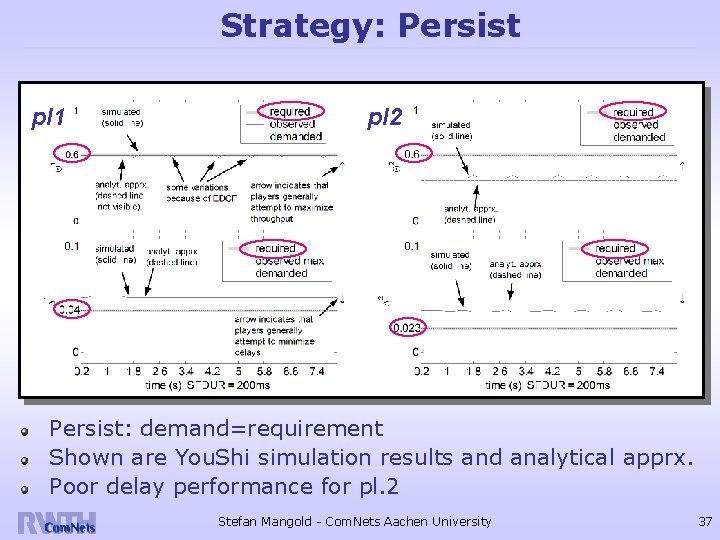
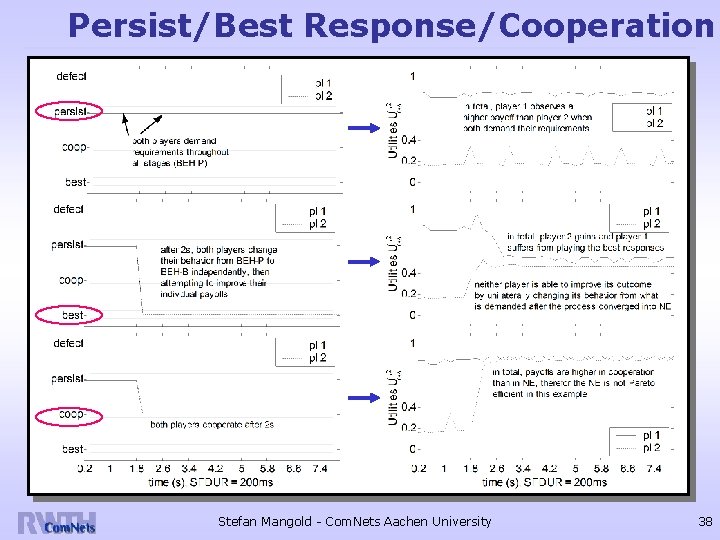
Strategy: Persist pl 1 pl 2 Persist: demand=requirement Shown are You. Shi simulation results and analytical apprx. Poor delay performance for pl. 2 Stefan Mangold - Com. Nets Aachen University 37

Persist/Best Response/Cooperation Stefan Mangold - Com. Nets Aachen University 38

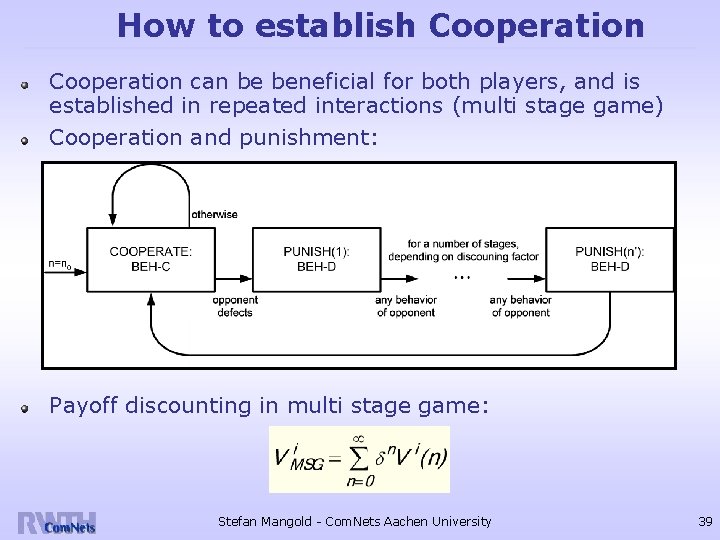
How to establish Cooperation can be beneficial for both players, and is established in repeated interactions (multi stage game) Cooperation and punishment: Payoff discounting in multi stage game: Stefan Mangold - Com. Nets Aachen University 39

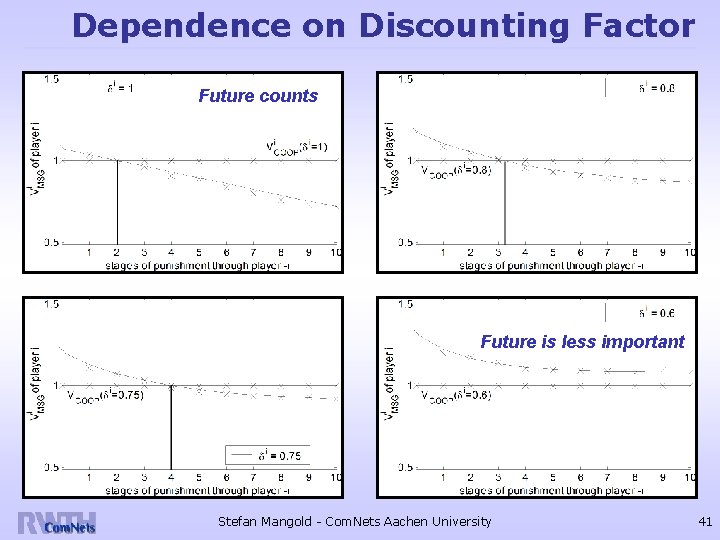
Condition for Cooperation It is more efficient to cooperate instead of defect (instead of playing best response), if… It depends on the discounting factor (importance/shadow of future) if mutual support is achievable: The more important the future is, the more likely is the establishment of cooperation For example, CCHCs will interact for many superframes Stefan Mangold - Com. Nets Aachen University 40

Dependence on Discounting Factor Future counts Future is less important Stefan Mangold - Com. Nets Aachen University 41

Wrap Up There is always a Nash equilibrium in the single stage game If the outcome of the Nash equilibrium is not satisfying, a player may attempt to punish the opponent, for establishment of mutual support Depending on the behaviors of the CCHCs (the interacting players), and their requirements, cooperation can be achieved Qo. S can be supported if cooperation is established Qo. S Support in legacy 802. 11? no! Qo. S Support in 802. 11 e EDCF? yes, but no guarantee! Qo. S Support with 802. 11 e HCF? not in unlicensed bands! Qo. S Support with shared radio resources? with mutual support: yes! Stefan Mangold - Com. Nets Aachen University 42

Conclusions IEEE 802. 11 e EDCF will provide basic means for Qo. S support The controlled medium access of HCF (polling) cannot support Qo. S in unlicensed frequency bands New analytical model for EDCF is developed allows to predict and control Qo. S New approach for coexisting radio networks may help radio networks operating in unlicensed bands to support Qo. S Results will be used in … Contributions to IEEE 802. 11 e IEEE 802. 19 coexistence discussions Spectrum etiquette development at Wi-Fi alliance Development of Spectrum Agile Radios (DARPA) Stefan Mangold - Com. Nets Aachen University 43

Backup Slides

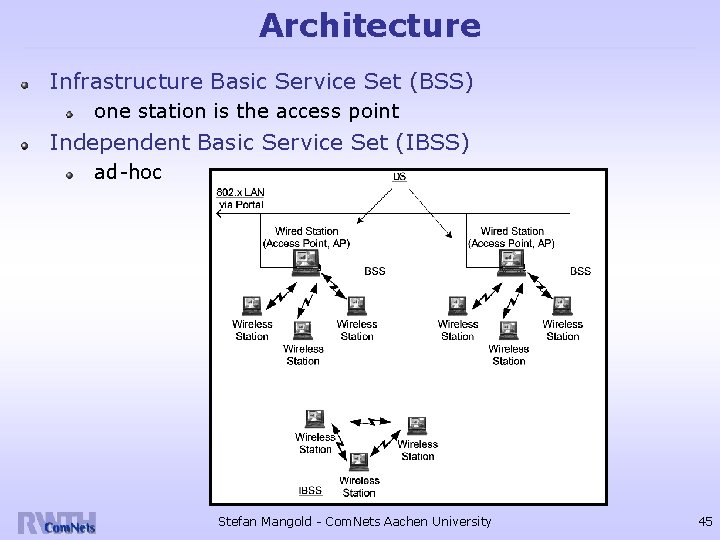
Architecture Infrastructure Basic Service Set (BSS) one station is the access point Independent Basic Service Set (IBSS) ad-hoc Stefan Mangold - Com. Nets Aachen University 45

Medium Access - Example Station 1 initiates frame exchange first Other stations set the Network Allocation Vector (NAV) Distributed approach difficult for station to support Qo. S Stefan Mangold - Com. Nets Aachen University 46

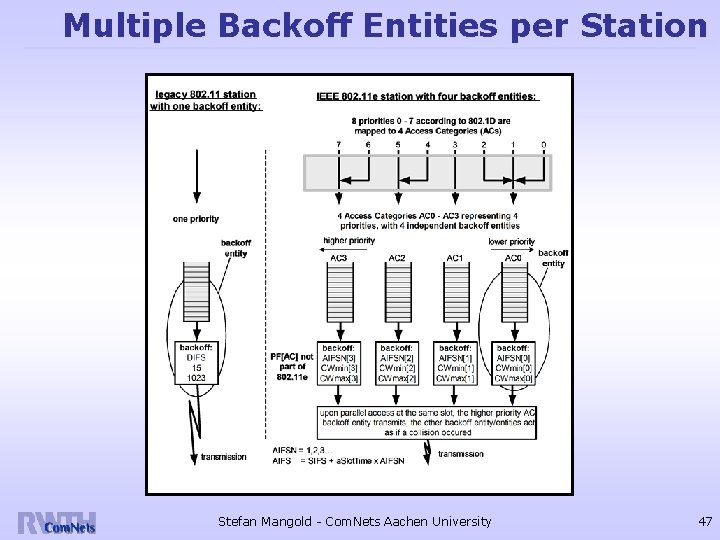
Multiple Backoff Entities per Station Stefan Mangold - Com. Nets Aachen University 47

Markov Chain State transition probabilities Stationary distributions Stefan Mangold - Com. Nets Aachen University 48

Allocation Process (Example) Two single stage games (two superframes): Two players interact with each other A third player models the EDCF background traffic For analysis, a formal description of this process is needed Stefan Mangold - Com. Nets Aachen University 49

Strategy: Best Response pl 1 pl 2 Best Response: adapt demand to achieve highest outcome (myopic competition) Action profile (demand) converges to NE Stefan Mangold - Com. Nets Aachen University 50

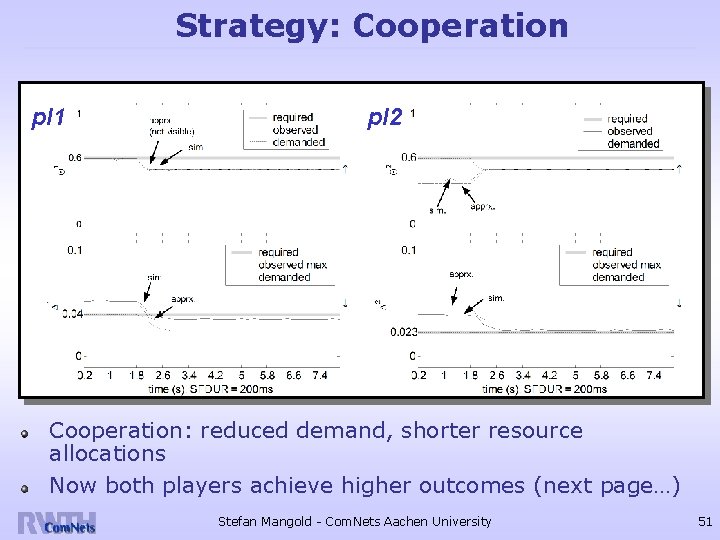
Strategy: Cooperation pl 1 pl 2 Cooperation: reduced demand, shorter resource allocations Now both players achieve higher outcomes (next page…) Stefan Mangold - Com. Nets Aachen University 51