Analysis of Concurrent Software Models Using Partial Order

Analysis of Concurrent Software Models Using Partial Order Views Qiang Sun, sun-qiang@sjtu. edu. cn Yuting Chen, chenyt@cs. sjtu. edu. cn Jianjun Zhao, zhao-jj@cs. sjtu. edu. cn Shanghai Jiaotong University 17 -Oct-21

Outline • Motivation • An approach to analysis of concurrent software models using partial order views • Some simple examples

Motivation • Checking and analyzing the software design model become crucial • Analysis of concurrent software behavioural models still faces challenges – Data races, atomicity violations, bugs • A number of analyses are on the basis of state models – A process can be modeled as a state machine in which the transitions are atomic or indivisible actions executed by the process. – LTS: Labeled Transition Systems – FSP (Finite State Processes), CCS, CSP

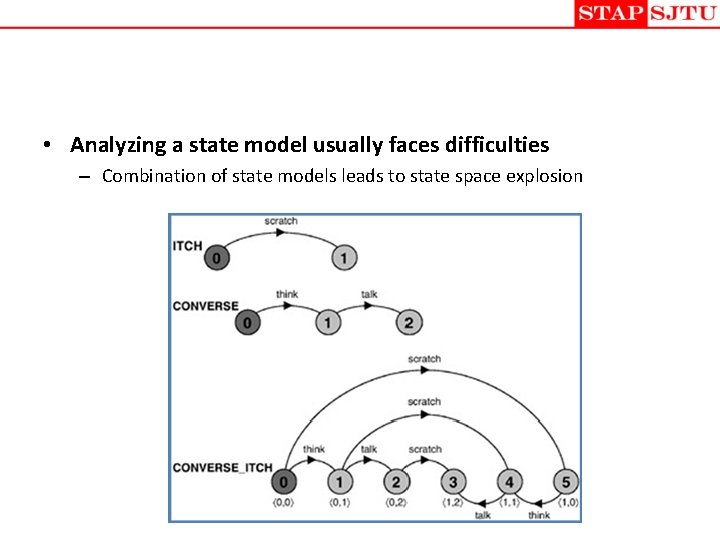
• Analyzing a state model usually faces difficulties – Combination of state models leads to state space explosion

Solution? • Modeling concurrency using partial orders – Partial order view • Extraction of partial orders of interest events from state machines – Partial orders can also be extracted from partial behavioral models. • Bi. G provides the mechanism of the model transformation and synchronization. – State machine ↔ Pomset model

Labeled Partial Order (LPO) – A partial order is a pair (E, <), where < is an irreflexive transitive binary relation on the vertex set E. – A labeled partial order (lpo) is a structure (E, ∑, μ, <), where (E, <) is a partial order, and μ : E→∑ labels the vertices of E with elements of the set ∑. – (E, ∑, μ, <) and (E’, ∑’, μ’, <’) over the same set of labels ∑ are isomorphic if – there exists a bijection τ: E→E’ such that for all u, v ∈ E, μ(u)= μ’(τ(u)), and u < v iff τ(u) <’ τ(v).

Partial Order Multi-Set (Pomset) • A pomset [E, ∑, μ, <] is the isomorphism class of an lpo (E, ∑, μ, <). – A pomset [E, ∑, μ, <] is finite if E is finite. – Two pomsets [E, ∑, μ, <] and [E’, ∑’, μ’, <’] are isomorphic if • there exist bijections τ : E→E’ and ν: ∑ → ∑’, such that for all u, v ∈ E and for all a ∈ ∑, μ(u) = a iff μ’ (μ(u)) = ν(a), and u < v iff τ(u) <’τ(v).

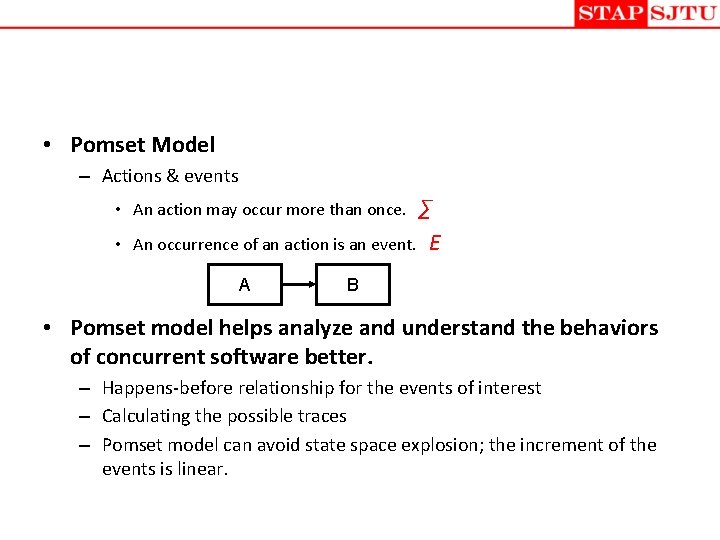
• Pomset Model – Actions & events ∑ An occurrence of an action is an event. E • An action may occur more than once. • A B • Pomset model helps analyze and understand the behaviors of concurrent software better. – Happens-before relationship for the events of interest – Calculating the possible traces – Pomset model can avoid state space explosion; the increment of the events is linear.

Analysis of Concurrent Software Models Using Partial Order Views • To extract pomset model – Computing the partial order of events within one process. – Merging partial orders of different processes through parallel operation. • To analyze pomset model and check event traces • To revisit state model whether we detect abnormal event traces • Bidirectional Graph Transformation technique provides with support in transforming state model to pomset model and keeping model synchronization. – The result can be easily mapped back to the original LTS.

SMALL EXAMPLES

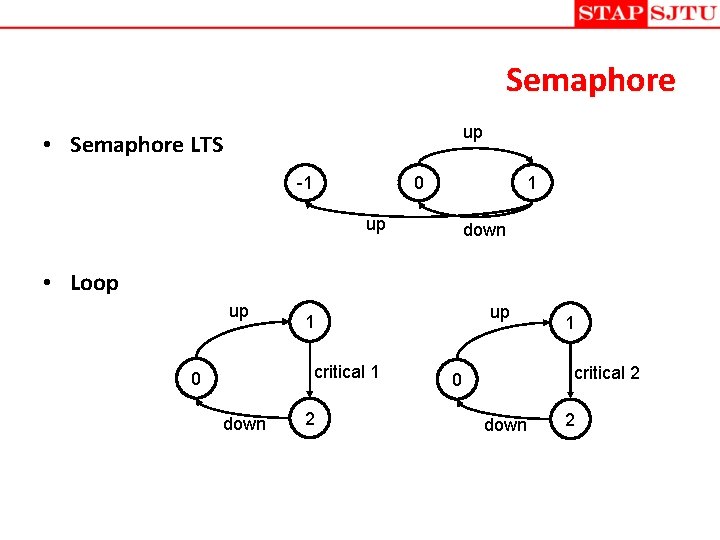
Semaphore up • Semaphore LTS -1 1 0 up down • Loop up critical 1 0 down up 1 2 1 critical 2 0 down 2

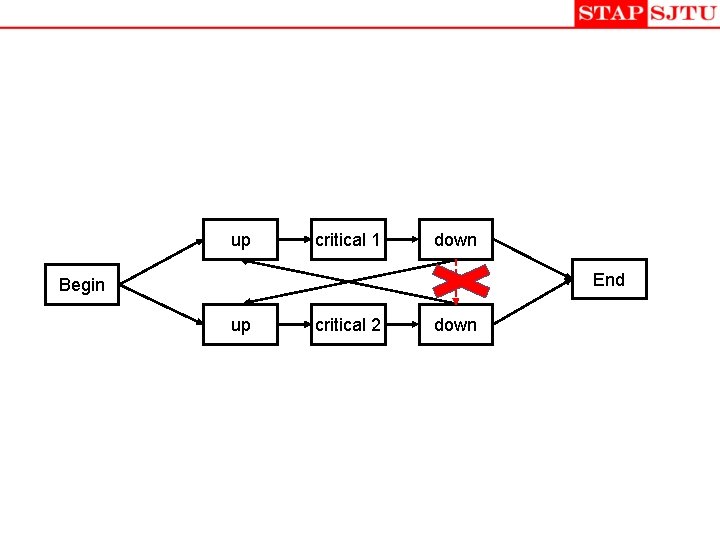
up critical 1 down End Begin up critical 2 down

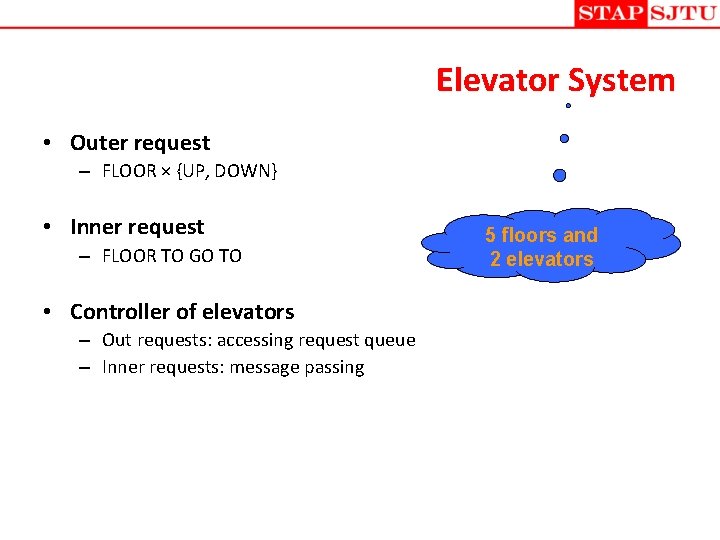
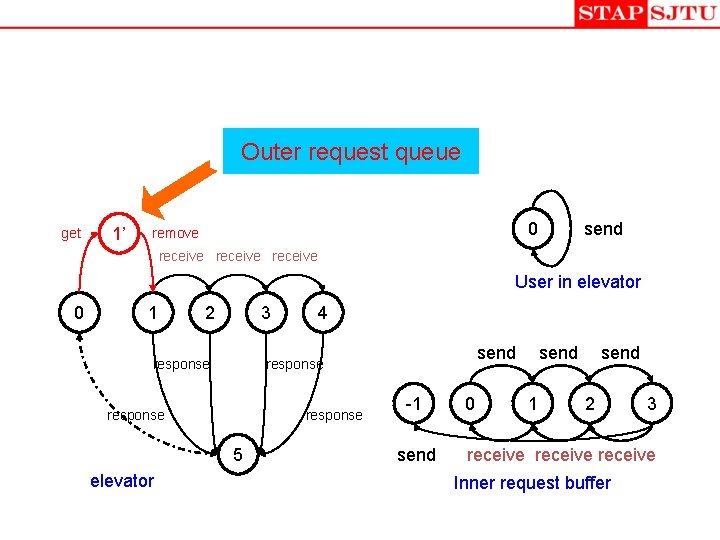
Elevator System • Outer request – FLOOR × {UP, DOWN} • Inner request – FLOOR TO GO TO • Controller of elevators – Out requests: accessing request queue – Inner requests: message passing 5 floors and 2 elevators

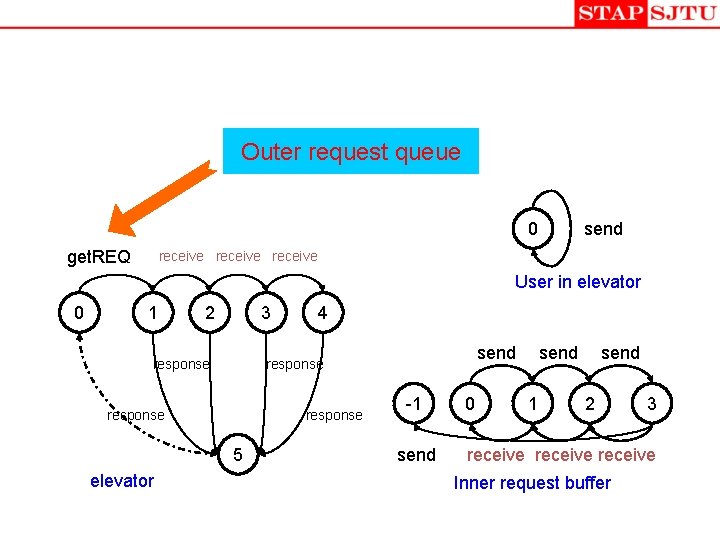
Outer request queue 0 get. REQ send receive User in elevator 0 1 2 3 response send response 5 elevator 4 -1 send 0 send 1 send 2 3 receive Inner request buffer

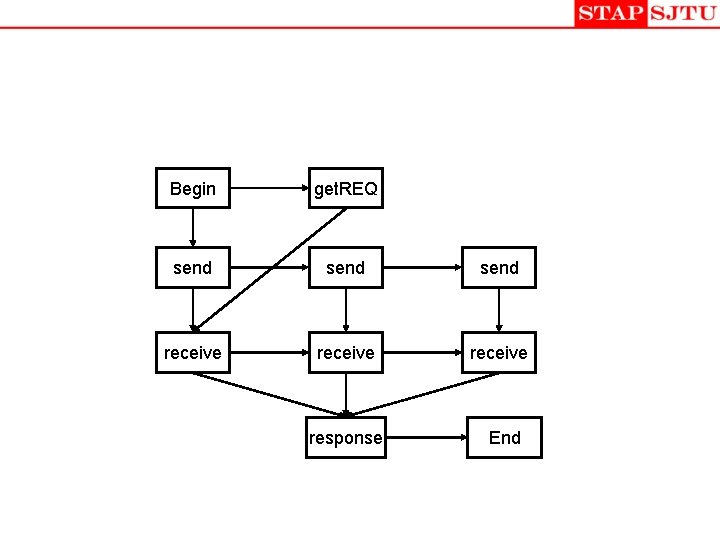
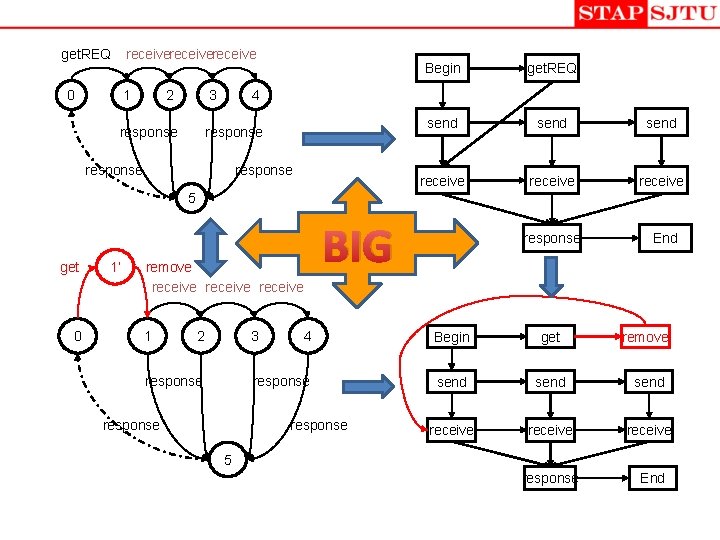
Begin get. REQ send receive response End

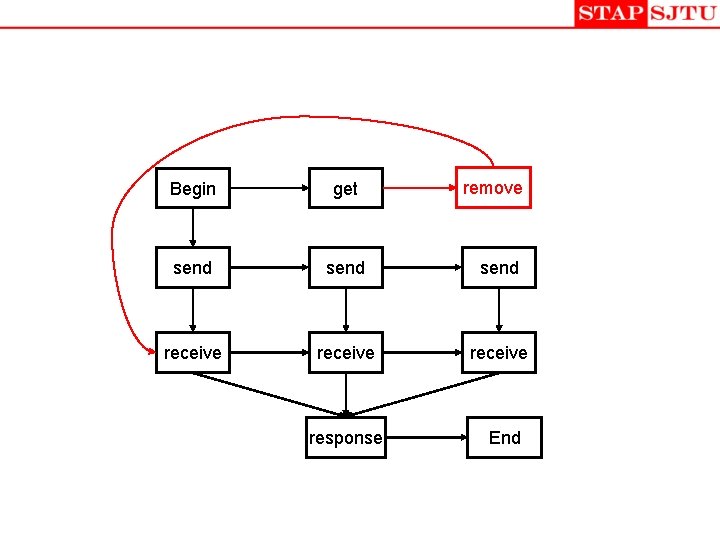
remove Begin get send receive response End

Outer request queue get 1’ 0 remove send receive User in elevator 0 1 2 3 response send response 5 elevator 4 -1 send 0 send 1 send 2 3 receive Inner request buffer

receivereceive get. REQ 0 1 2 3 response Begin get. REQ send receive response End 4 response 5 get 0 1’ BIG remove receive 1 2 3 response 4 Begin get remove response send receive response End response 5

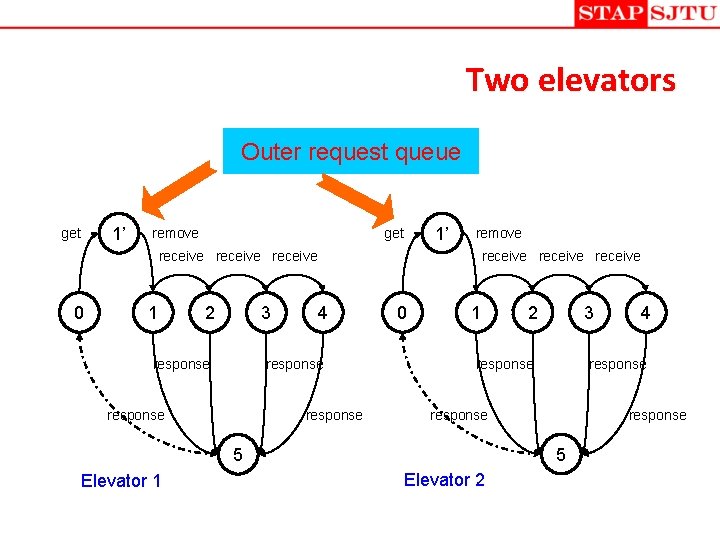
Two elevators Outer request queue 1’ get remove receive receive 0 1 2 3 response 4 response 0 1 3 response 5 Elevator 2 4 response 5 Elevator 1 2

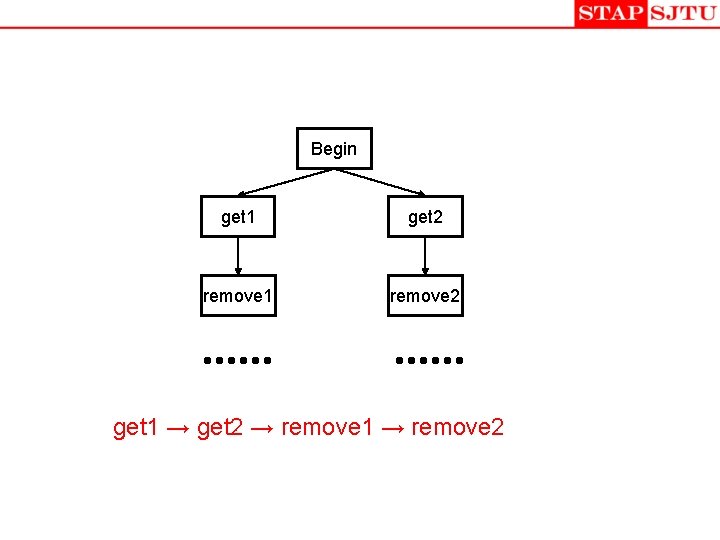
Begin get 1 get 2 remove 1 remove 2 get 1 → get 2 → remove 1 → remove 2

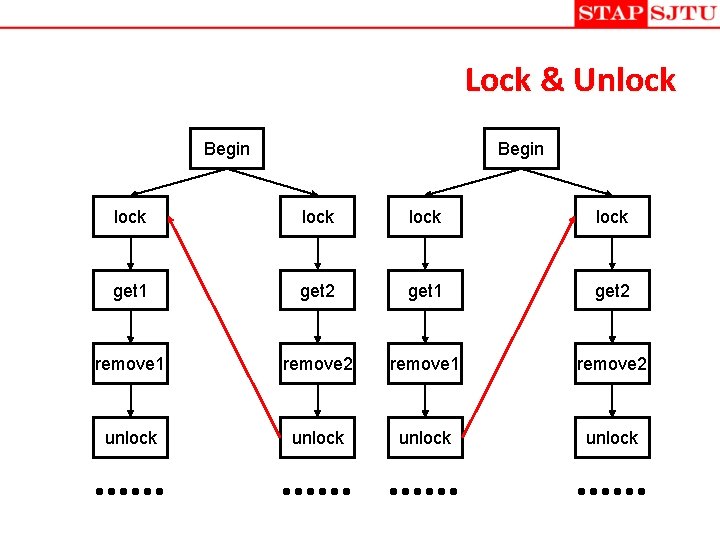
Lock & Unlock Begin lock get 1 get 2 remove 1 remove 2 unlock

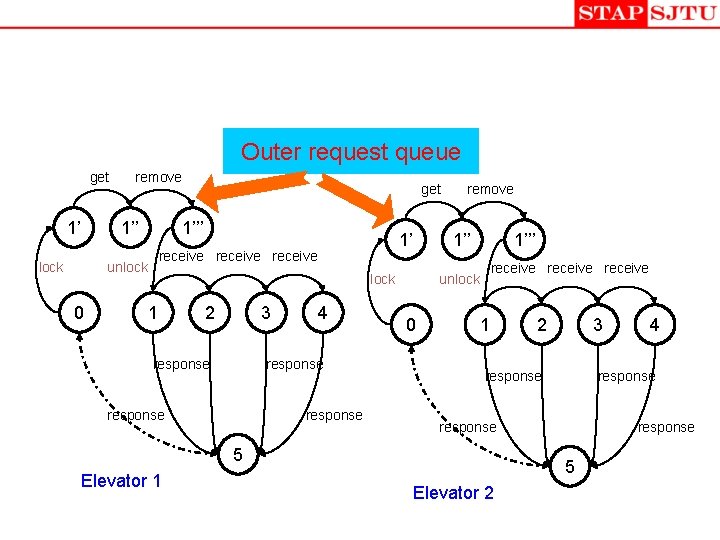
Outer request queue get 1’ remove 1’’’ 0 1’ receive unlock get 1’’ 2 3 response 4 response 1’’’ receive unlock 1 remove 0 1 3 response 5 Elevator 2 4 response 5 Elevator 1 2

• Partial order event model provides engineers with – A different view about the events occurring in the concurrent software system and their order. – Bidirectional model transformation technique helps transform state model to partial order event model • Detection of potential errors is possible from taking advantage of information about partial order event model – To detect data races by associating the events to accessing the shared memory – To detect atomicity violations by associating actions to accessing resources – Determination of the real bugs usually relies on human judgements – Bidirectional model transformation technique helps reveal the bugs in the state model if any abnormal event traces are found

Conclusions • State model is widely used in practice • Pomset model can avoid state space explosion • An approach to checking and analyzing state model using pomset model • Bi. G provides the mechanism of model transformation and bug elimination

Future Work • A systematic approach • Correctness of the approach – Case studies and experiments • Tool Support