Analysis of Bubble Sort and Loop Invariant N1

Analysis of Bubble Sort and Loop Invariant

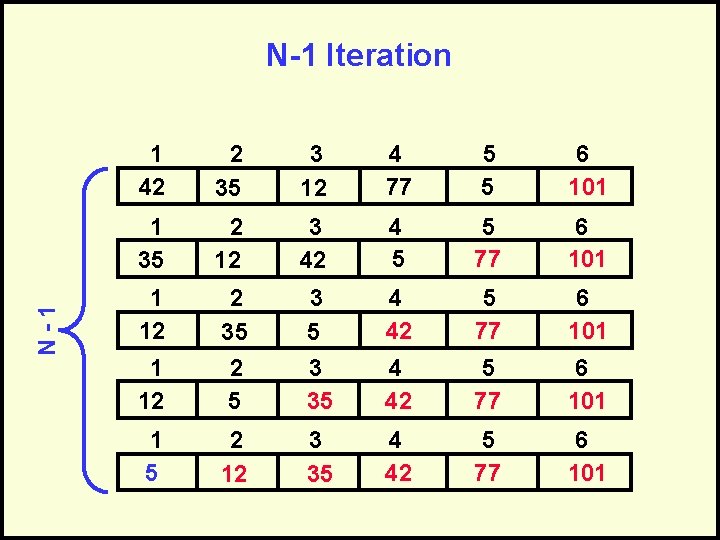
N-1 Iteration 1 42 2 35 3 12 4 77 5 5 6 101 1 35 2 12 3 42 4 5 5 77 6 101 1 12 3 5 3 35 4 42 5 77 6 101 1 12 2 35 2 5 4 42 5 77 6 101 1 5 2 12 3 35 4 42 5 77 6 101

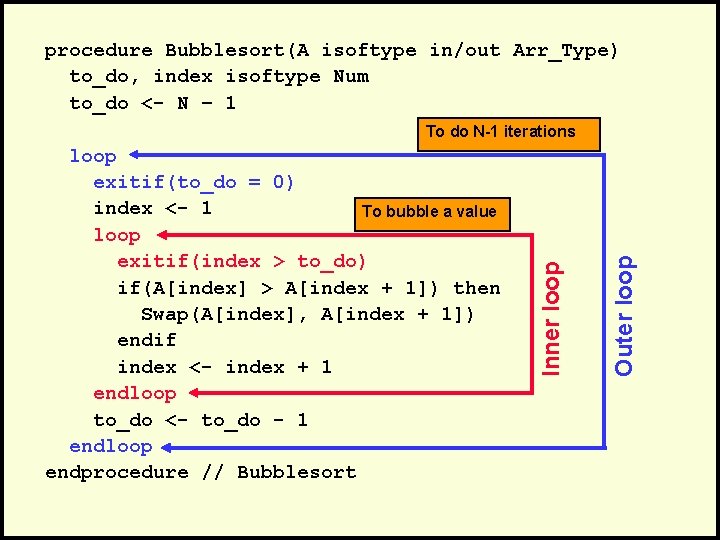
procedure Bubblesort(A isoftype in/out Arr_Type) to_do, index isoftype Num to_do <- N – 1 Outer loop exitif(to_do = 0) index <- 1 To bubble a value loop exitif(index > to_do) if(A[index] > A[index + 1]) then Swap(A[index], A[index + 1]) endif index <- index + 1 endloop to_do <- to_do - 1 endloop endprocedure // Bubblesort Inner loop To do N-1 iterations

Bubble Sort Time Complexity • Best-Case Time Complexity – The scenario under which the algorithm will do the least amount of work (finish the fastest) • Worst-Case Time Complexity – The scenario under which the algorithm will do the largest amount of work (finish the slowest)

Bubble Sort Time Complexity Called Linear Time O(N) Order-of-N • Best-Case Time Complexity – Array is already sorted – Need 1 iteration with (N-1) comparisons Called Quadratic Time O(N 2) Order-of-N-square • Worst-Case Time Complexity – Need N-1 iterations – (N-1) + (N-2) + (N-3) + …. + (1) = (N-1)* N / 2

Loop Invariant • It is a condition or property that is guaranteed to be correct with each iteration in the loop • Usually used to prove the correctness of the algorithm

Loop Invariant for Bubble Sort • By the end of iteration i the right-most i items (largest) are sorted and in place

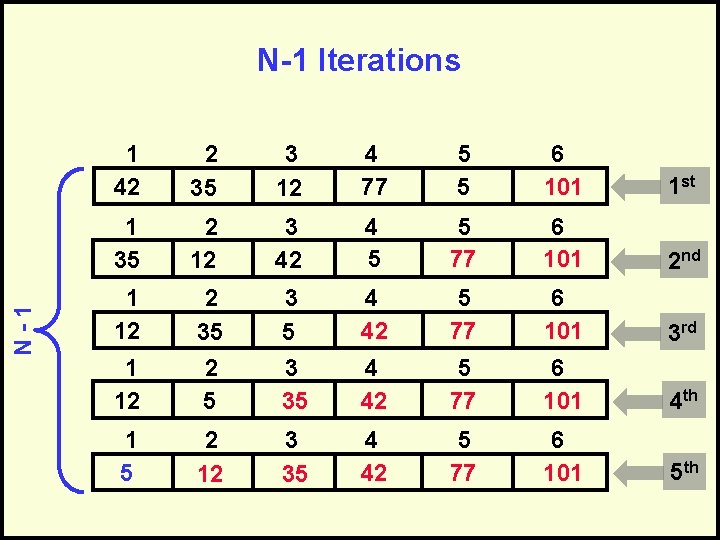
N-1 Iterations 1 42 2 35 3 12 4 77 5 5 6 101 1 st 1 35 2 12 3 42 4 5 5 77 6 101 2 nd 1 12 3 5 3 35 4 42 5 77 6 101 3 rd 1 12 2 35 2 5 4 42 5 77 6 101 4 th 1 5 2 12 3 35 4 42 5 77 6 101 5 th

Correctness of Bubble Sort (using Loop Invariant) • Bubble sort has N-1 Iterations • Invariant: By the end of iteration i the right-most i items (largest) are sorted and in place • Then: After the N-1 iterations The right-most N-1 items are sorted – This implies that all the N items are sorted

Correctness of Bubble Sort (using Loop Invariant) • What if we stop early (after iteration K) – Remember the Boolean “did_swap” flag • From the invariant the right-most K items are sorted – A[N-(K-1)] < A[N-2] < A[N-1] < A[N] • Since we stopped early, then no swaps are done, Then – A[1] < A[2] < …. . < A[N-K] • By merging these two, then the entire array is sorted