Analysis of Basic Load Cases Axial Stress Tension

Analysis of Basic Load Cases • Axial Stress • Tension and Compression • Shear Stress • Examples • Bending • Tension/Compression & Shear • Torsion • Shear stress

Axial Stress F= Axial Force (Newtons, N) A = Cross-Sectional Area Perpendicular to “F” (mm 2) E = Young’s Modulus of Material, MPa L = Original Length of Component, mm s = Average Stress (N/mm 2 or MPa) D = Total Deformation (mm) AE = “Axial Stiffness of Component”

Direct Shear Stress t P A average = Avearge Shear Stress (MPa) = Shear Load = Area of Material Resisting “P”

Examples of Direct Shear Stress D Bolted Joint with Two Shear Planes. P D = 50 KN = 13 mm tavg = ? Area of bolt (Ab) = p D 2 / 4 = p (13)2 / 4 = 132. 7 mm 2 A resisting shear = 2 Ab tavg = P / 2 Ab = 50000 N/ 2(132. 7) mm 2 = 188. 4 MPa

Direct Shear II 13 150 13 175 Fillet Weld 9. 2 Find the load P, such that the stress in the weld does not exceed the allowable stress limit of 80 MPa.

Solution: tavg = P / Aw = 80 MPa Aw = Throat x Total Length = (9. 2)(175)(2) = 3217 mm 2 P / 3217 = 80 MPa P = (3217)(80) N = 257386 N = 257 k. N

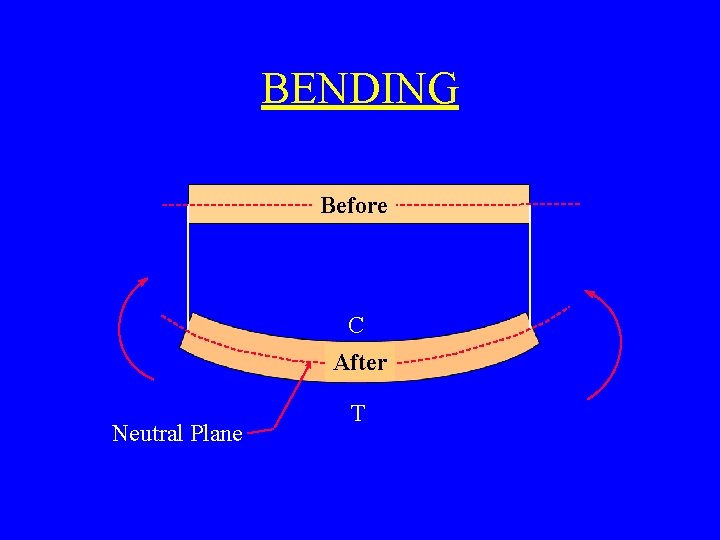
BENDING Before C After Neutral Plane T

Displacement in Beam y v Curvature of Beam = Moment; EI = Bending stiffness of Beam x

Bending Stress smax (C) y s cc ct smax (T)

Source of Internal Moment Fc Ft Fc = Ft M= Ft d d

Equivalent FBD F M = Fd d F

Bending Stiffness EI = Bending Stiffness E = Young’s Modulus (Material Dependant) I = Moment of Inertia (2 nd Moment of Area) y Ixx = bh 3 / 12 (mm 4) h Iyy= hb 3 / 12 (mm 4) y b

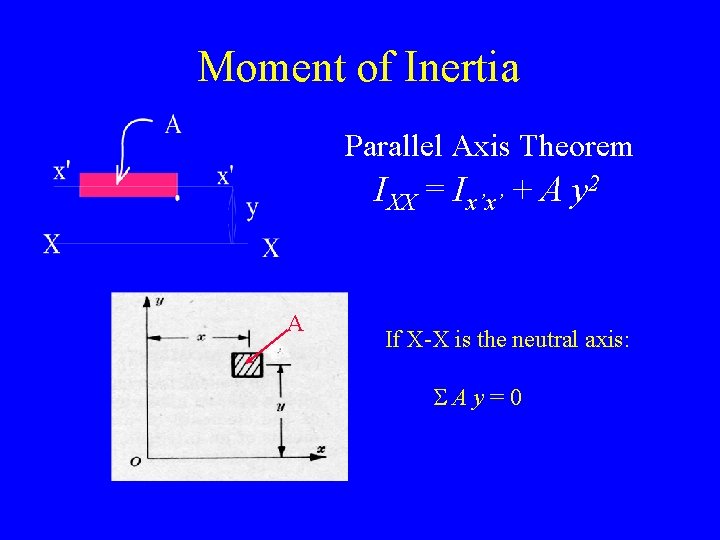
Moment of Inertia Parallel Axis Theorem IXX = Ix’x’ + A y 2 A If X-X is the neutral axis: SAy=0

Try it! Locate the Neutral Axis and find the Moment of Inertia for the “T” section shown below. Consider the XX axis, all dimensions are mm. Ans: Ct = 200 mm Ixx = 2. 50 x 108 mm 4 X X 250 50 300 Ct 60

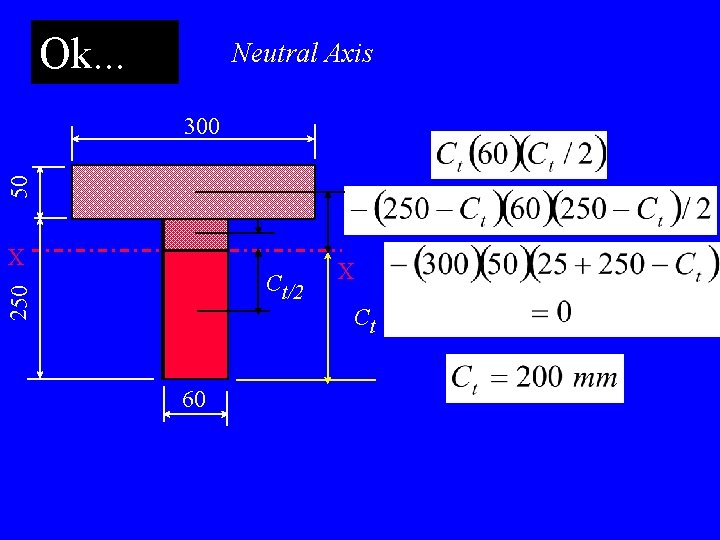
Ok. . . Neutral Axis 50 300 X 250 Ct/2 60 X Ct

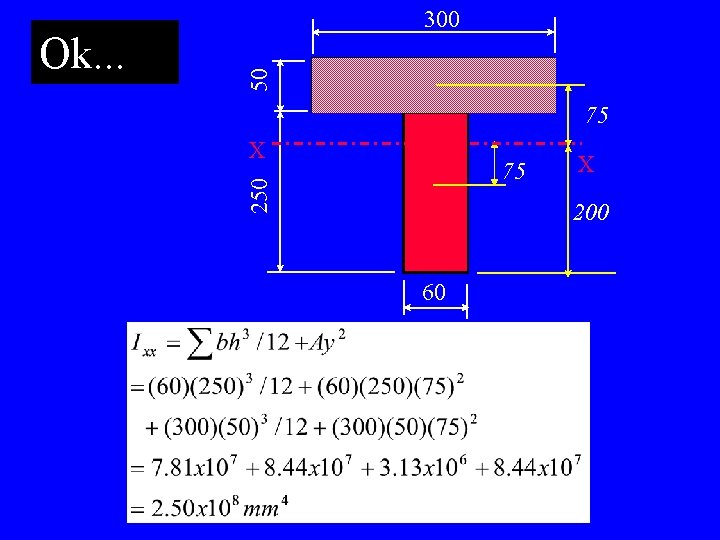
50 75 X 75 250 Ok. . . 300 X 200 60 Mech 422 – Stress and Strain Analysis

Determine the Bending Stiffness of beams with this cross section made of: 1) Steel, E=203 000 MPa 2) Aluminum Alloy, E= 72 000 MPa 3) Glass Reinforced Polyester, E = 30 000 MPa

Determine the Bending Stiffness of beams with this cross section made of: 1) Steel, E=203 000 MPa 2) Aluminum Alloy, E= 72 000 MPa 3) Glass Reinforced Polyester, E = 30 000 MPa Ans: 1) EI = 5. 08 x 1013 Nmm 2 2) EI = 1. 80 x 1013 Nmm 2 3) EI = 0. 75 x 1013 Nmm 2 In the ratio 1 : 0. 36 : 0. 15

Bending Stress: 300 k. N 100 KN 200 KN M max = 200 KN. m s tension = 200 x 106 N. mm (200) mm / 2. 50 x 108 mm 4 = 160 MPa MAX s compression = 200 x 106 N. mm (100) mm / 2. 50 x 108 mm 4 = 80 MPa

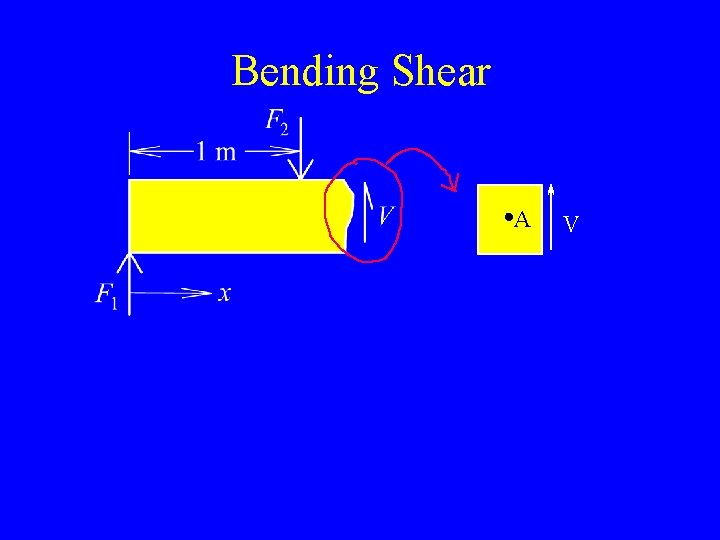
Bending Shear A V

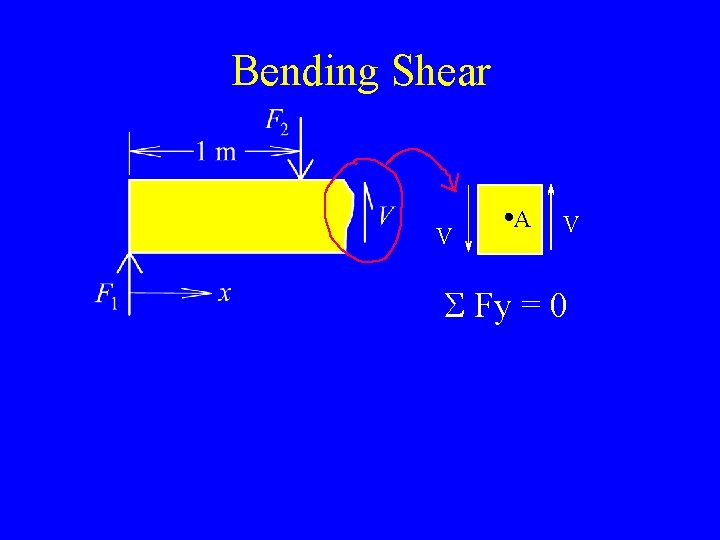
Bending Shear V A V S Fy = 0

Bending Shear V V A V V S Fy = 0 S Fx = 0 SM =0

Shear Stress - Bending y b t max h For a Rectangle: t avg = V / A t max = 1. 5 V / A A=bh t avg Max Shear Stress is at N. A.

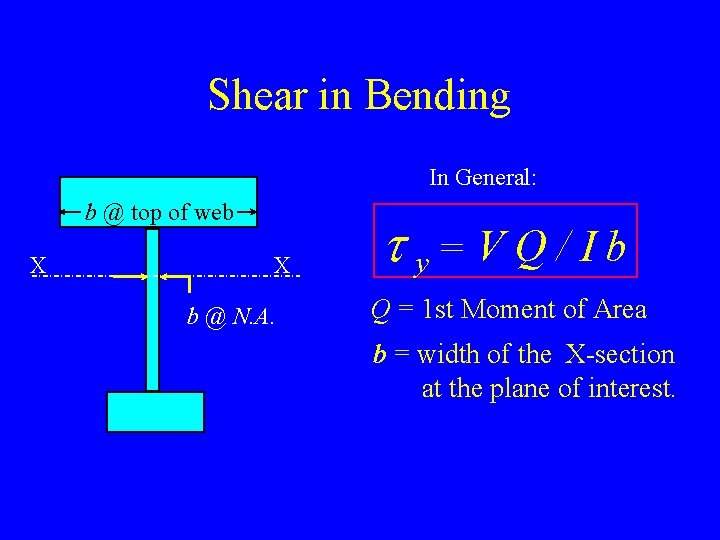
Shear in Bending In General: b @ top of web X X b @ N. A. t y= V Q / I b Q = 1 st Moment of Area b = width of the X-section at the plane of interest.

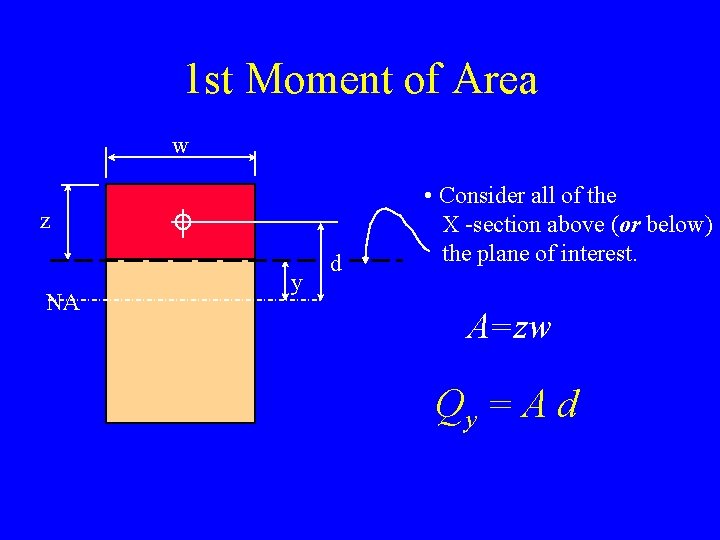
1 st Moment of Area w z NA y d • Consider all of the X -section above (or below) the plane of interest. A=zw Qy = A d

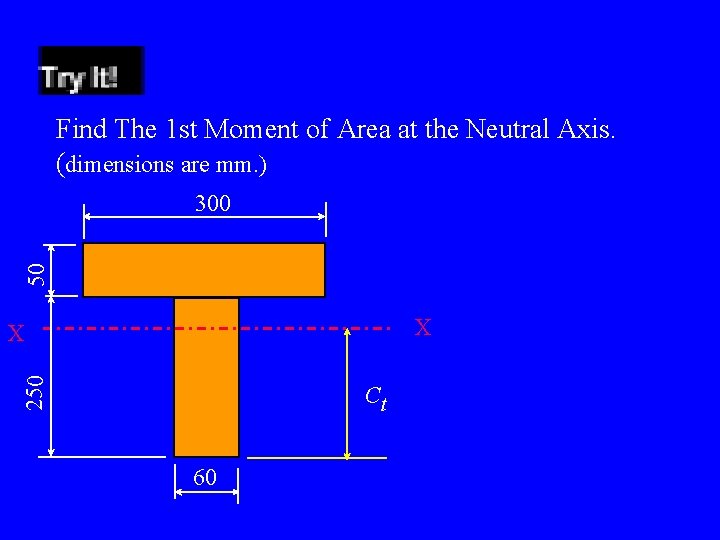
Find The 1 st Moment of Area at the Neutral Axis. (dimensions are mm. ) 50 300 X 250 X Ct 60

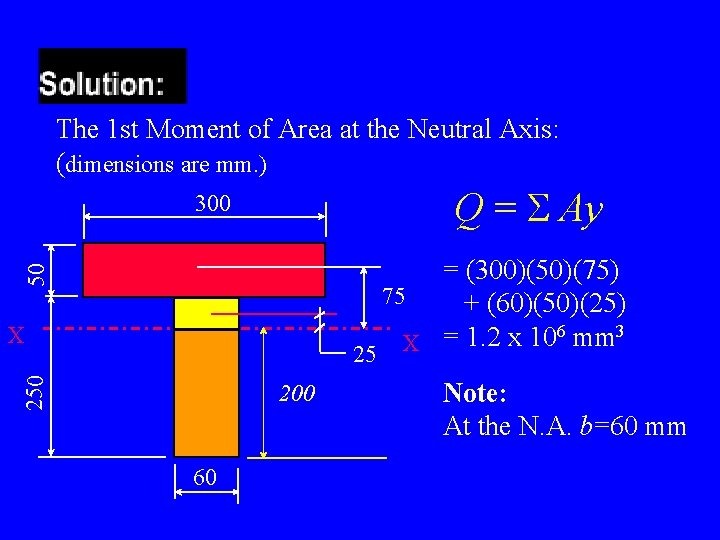
The 1 st Moment of Area at the Neutral Axis: (dimensions are mm. ) Q = S Ay 50 300 250 X 200 60 = (300)(50)(75) 75 + (60)(50)(25) = 1. 2 x 106 mm 3 X 25 Note: At the N. A. b=60 mm

Shear Stress: 300 k. N 100 k. N 200 k. N V max = 2000 KN t y= V Q / I b t max = (200 x 103 N) (1. 2 x 106 mm 3) (2. 50 x 108 mm 4 (60) mm = 16 MPa t avg = V/Aweb = (200 x 103 N) / (60)(300) mm 2 = 11. 1 MPa

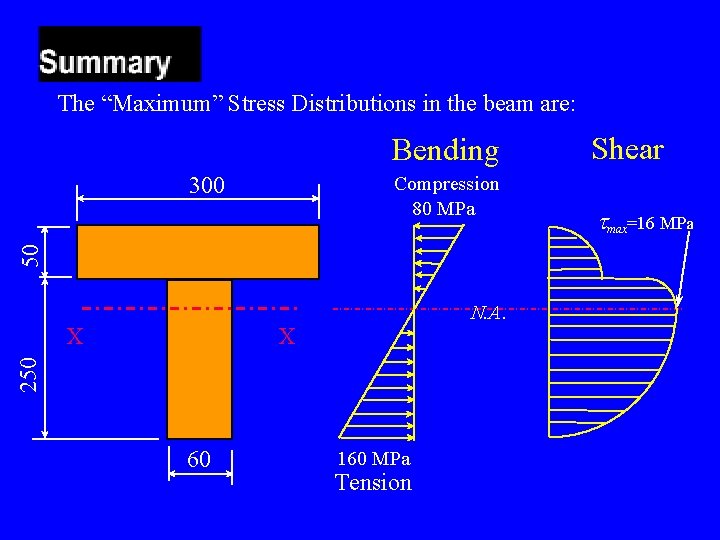
The “Maximum” Stress Distributions in the beam are: Bending 300 50 Compression 80 MPa N. A. X 250 X 60 160 MPa Tension Shear tmax=16 MPa

Torsion r T = Torque, G = Shear Modulus of Elasticity L = Length of Shaft, J = Polar Moment of Inertia q is in Radians!

Shear Stress Distribution tmax r D

Polar Moment of Inertia Di Do

Shear Modulus, G E = Young’s Modulus v = Poisson’s Ratio Example: Steel E = 203 000 MPa, v = 0. 3 G = 78 000 MPa

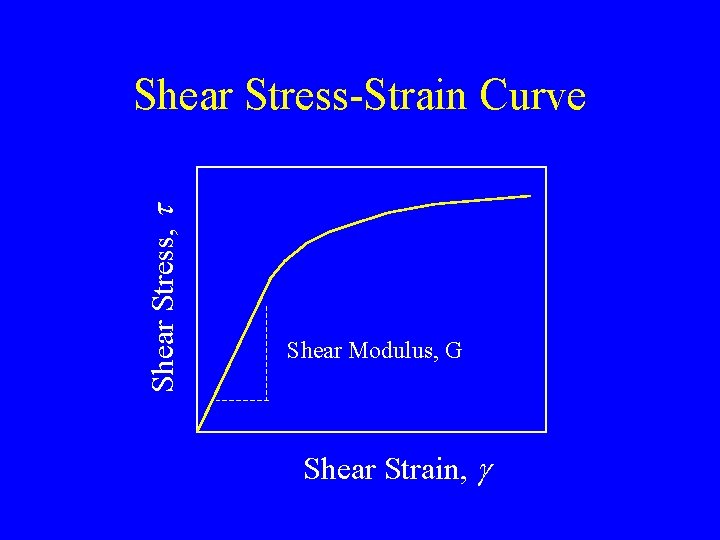
Shear Stress, t Shear Stress-Strain Curve Shear Modulus, G Shear Strain, g

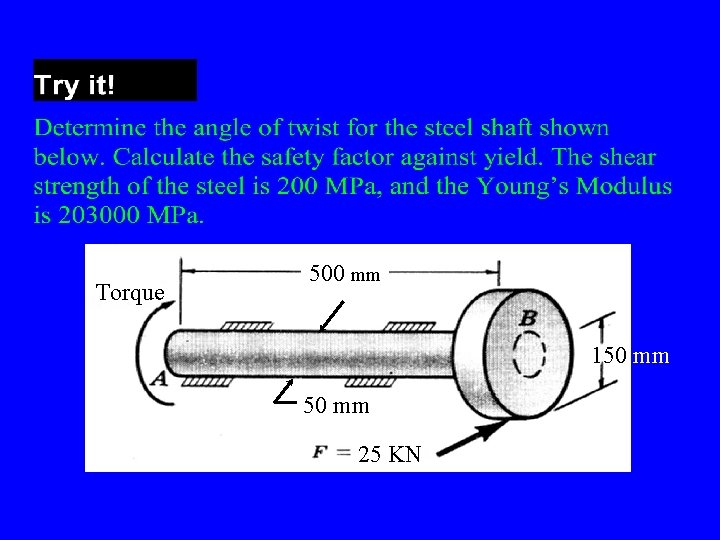
Torque 500 mm 150 mm 25 KN

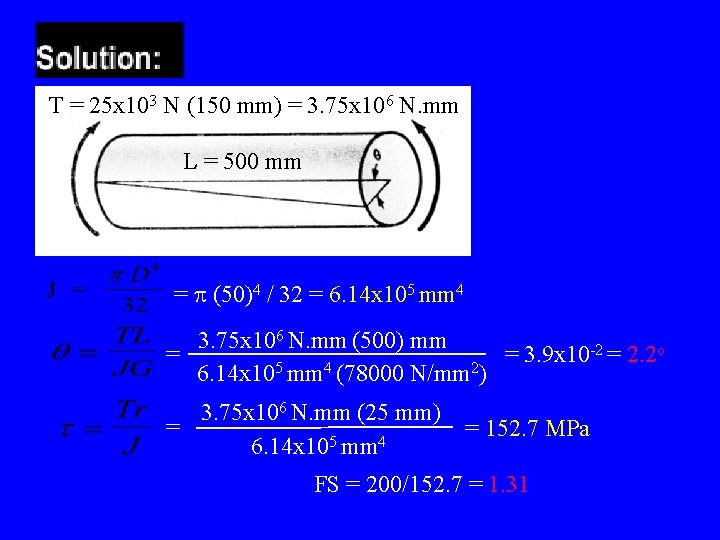
T = 25 x 103 N (150 mm) = 3. 75 x 106 N. mm L = 500 mm = p (50)4 / 32 = 6. 14 x 105 mm 4 3. 75 x 106 N. mm (500) mm -2 = 2. 2 o = 3. 9 x 10 = 6. 14 x 105 mm 4 (78000 N/mm 2) 3. 75 x 106 N. mm (25 mm) = 6. 14 x 105 mm 4 = 152. 7 MPa FS = 200/152. 7 = 1. 31

Superposition Assume the beam in our example is made of steel with a yield stress of 350 MPa. If it is subjected to an additional Axial Tension of 5000 k. N along it N. A. , will it yield ? 300 k. N F = 5000 KN 200 k. N 100 k. N

Result: Bending Axial Compression 80 MPa F/A = 167 MPa N. A. + Net 83 MPa (Tension) Tension = Tension < 350 MPa No Yield! 160 MPa Tension 327 MPa

Rule for Adding Stresses: Like stresses at a point acting in the same direction and on the same plane can be added algebraically. • You can’t add a shear stress to a tensile/compressive stress. • You can’t add a stress in one location to one at another. • The effects of combined shear and tension/compression are covered later in this course.