Analysis Design of Algorithms CSCE 321 Prof Amr

Analysis & Design of Algorithms (CSCE 321) Prof. Amr Goneid Department of Computer Science, AUC Part 2. Types of Complexities Prof. Amr Goneid, AUC 1

Types of Complexities Prof. Amr Goneid, AUC 2

Types of Complexities n Rules for Upper Bound n Comparing Complexities n Types of Complexities Prof. Amr Goneid, AUC 3

1. Rules for Upper Bound n If (k) is a constant, then: O(k) O(n) and O(k f(n)) = O(f(n)) n e. g. an 2 and bn 2 are both O(n 2) T(n) O(kn) O(k) n Prof. Amr Goneid, AUC 4

Rules for Big O n The growth rate of a sum of terms of is the growth rate of its fastest growing term O(f(n)) + O(g(n)) = max(O(f(n)) , O(g(n))) n e. g. f(n) = 2 n = O(n), g(n) = 0. 1 n 3 = O(n 3) T(n) = max(O(n) , O(n 3)) = O(n 3) 2 n O(n 3) 0. 1 n 3 Prof. Amr Goneid, AUC 5

Rules for Big O n The product of big-O’s is the big-O of the products: O(f(n)) * O(g(n)) = O(f(n) * g(n)) n e. g. T 1(n) = O(n), T 2(n) = O(n 2) T(n) = T 1 (n) * T 2 (n) = O(n 3) Repeat n times O(n 2) O(n 3) Prof. Amr Goneid, AUC 6

Rules for Big O n Logarithms grow slower than powers: O(loga n) O(nk) for all a > 1 and k > 0 n e. g. O(log n) < O(n) n Claim: For all n ≥ 1, log n ≤ n. Prove by induction on n. Prof. Amr Goneid, AUC 7

Rules for Big O n All logarithms grow at the same rate: loga n = (logb n) for all a , b > 1 n e. g. log 2 n = (log 3 n) n Proof: Prof. Amr Goneid, AUC 8

Rules for Big O n For a polynomial of degree m, n Prove! n O(nm-1) O(nm) follows from above Prof. Amr Goneid, AUC 9

Rules for Big O n Exponential functions grow faster than powers O(nk) < O(bn) for all k ≥ 0 and b > 1 n e. g. O(n 3) < O(2 n) n Proof: Prof. Amr Goneid, AUC 10

Summary of Rules for Big-O Rule Example For constant k, O(k) < O(n) O(7) = O(1) < O(n) For constant k, O(kf) = O(f) O(2 n) = O(n) O(|f|+|g|) = O(|f|) + O(|g|) = Max (O(|f|) , O(|g|) O(6 n 2+n)=O(6 n 2)+O(n) = O(n 2) Nesting of loop O(g) within a loop O(f) gives O(f*g) O(n 4*n 2)=O(n 6) O(nm-1) < O(nm) O(n 2) < O(n 3) O((log n)k) O(n) O(log n) < O(n) Prof. Amr Goneid, AUC 11

2. Comparing Complexities Dominance: n If lim(n-> ) f(n)/g(n) = then f(n) dominates (i. e. grows faster) n If lim(n-> ) f(n)/g(n) = 0 little oh then g(n) dominates. In the latter case, we say that f(n) = o(g(n)) n If lim(n-> ) f(n)/g(n) = constant then both grow at the same rate. Prof. Amr Goneid, AUC 12

Comparing Complexities Examples: n if a > b then na dominates nb Why? n n 2 dominates (3 n+2) Why? n n 2 dominates (n log n) Why? Prof. Amr Goneid, AUC 13

Using l’Hopital’s Rule (1696) Example: Show that f(n) = n(k+α) + nk (log n)2 and g(n) = k n(k+α) grow at the same rate. Prof. Amr Goneid, AUC 14

Comparing Complexities n Which grows faster: f(n) = n 3 or f(n) = n 0. 001 or f(n) = 2 n+1 or f(n) = 2 n or g(n) = n log n g(n) = 2 n g(n) = 22 n Prof. Amr Goneid, AUC 15

Exercises Which function has smaller complexity ? n f = 100 n 4 g = n 5 n f = log(log n 3) g = log n n f = n 2 g = n log n n f = 50 n 5 + n 2 + n g = n 5 n f = en g = n! Prof. Amr Goneid, AUC 16

3. Types of Complexities n Constant Complexity n T(n) = constant independent of (n) n Runs in constant amount of time O(1) n Example: cout << a[0][0] Prof. Amr Goneid, AUC 17

Types of Complexities n Logarithmic Complexity n Log 2 n = m is equivalent to n=2 m n Reduces the problem to half O(log 2 n) n Example: Binary Search T(n) = O(log 2 n) Much faster than Linear Search which has T(n) = O(n) Prof. Amr Goneid, AUC 18

Linear vs Logarithmic Complexities T(n) O(log 2 n) n Prof. Amr Goneid, AUC 19

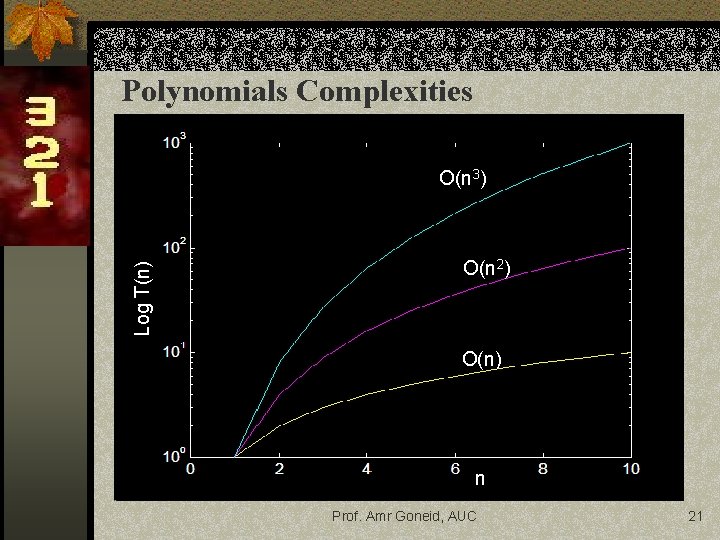
Types of Complexities n Polynomial Complexity n T(n) = amnm+…+ a 2 n 2 + a 1 n 1 + a 0 n If m=1, then O(a 1 n+a 0) O(n) n If m > 1, then O(nm) as nm dominates Prof. Amr Goneid, AUC 20

Polynomials Complexities Log T(n) O(n 3) O(n 2) O(n) n Prof. Amr Goneid, AUC 21

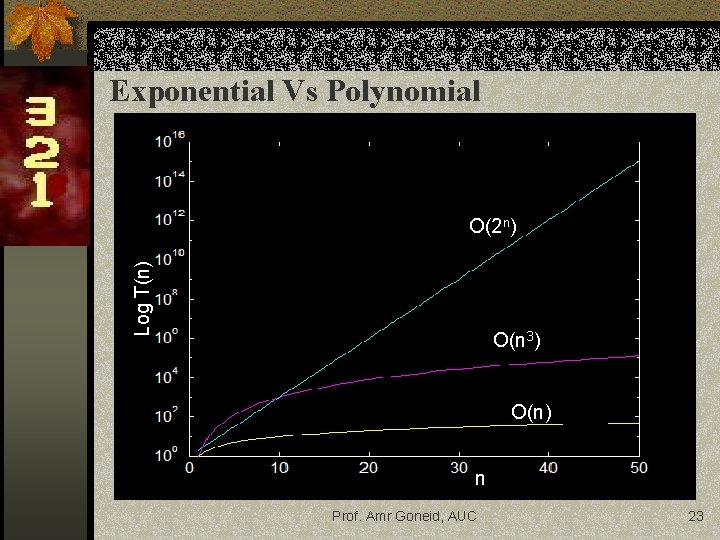
Types of Complexities n Exponential n Example: List all the subsets of a set of n elements {a, b, c}, {a, b}, {a, c}, {b, c}, {a}, {b}, {c}, {} n Number of operations T(n) = O(2 n) n Exponential expansion of the problem O(an) where a is a constant greater than 1 Prof. Amr Goneid, AUC 22

Exponential Vs Polynomial Log T(n) O(2 n) O(n 3) O(n) n Prof. Amr Goneid, AUC 23

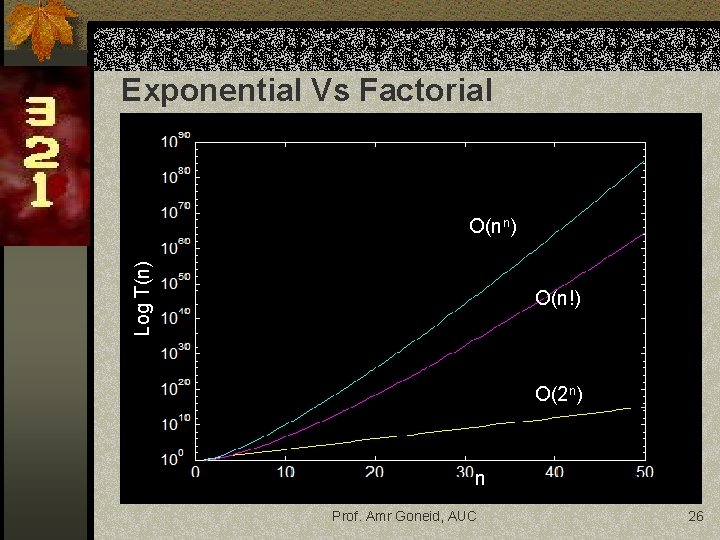
Types of Complexities n Factorial time Algorithms n Example: n Traveling salesperson problem (TSP): Find the best route to take in visiting n cities away from home. What are the number of possible routes? For 3 cities: (A, B, C) Prof. Amr Goneid, AUC 24

Possible routes in a TSP –Number of operations = 3!=6, Hence T(n) = n! –Expansion of the problem O(n!) Prof. Amr Goneid, AUC 25

Exponential Vs Factorial Log T(n) O(n!) O(2 n) n Prof. Amr Goneid, AUC 26

Execution Time Example n Example: n For the exponential algorithm of listing all subsets of a given set, assume the set size to be of 1024 elements n Number of operations is 21024 about 1. 8*10308 n If we can list a subset every nanosecond the process will take 5. 7 * 10291 yr!!! Prof. Amr Goneid, AUC 27

P and NP – Times n P (Polynomial) Times: O(1), O(log n)2, O(n), O(n log n), O(n 2), O(n 3), …. n NP (Non-Polynomial) Times: O(2 n) , O(en) , O(n!) , O(nn) , …. . Prof. Amr Goneid, AUC 28

P and NP – Times n Polynomial time is GOOD Try to reduce the polynomial power n NP (e. g. Exponential) Time is BAD Prof. Amr Goneid, AUC 29