Analysis and processing of Diffusion Weighted MRI Supervised

Analysis and processing of Diffusion Weighted MRI Supervised by: Remco Duits Anna Vilanova Luc Florack Collaboration: with Slide 1 of 31 Tom Dela Haije Rutger Fick

Overview of presentation 1) Short introduction to DW-MRI 2) Enhancement of DW-MRI data 3) Fiber tracking Slide 2 of 31

Diffusion of water Diffusion is dependent on orientation Slide 3 of 31

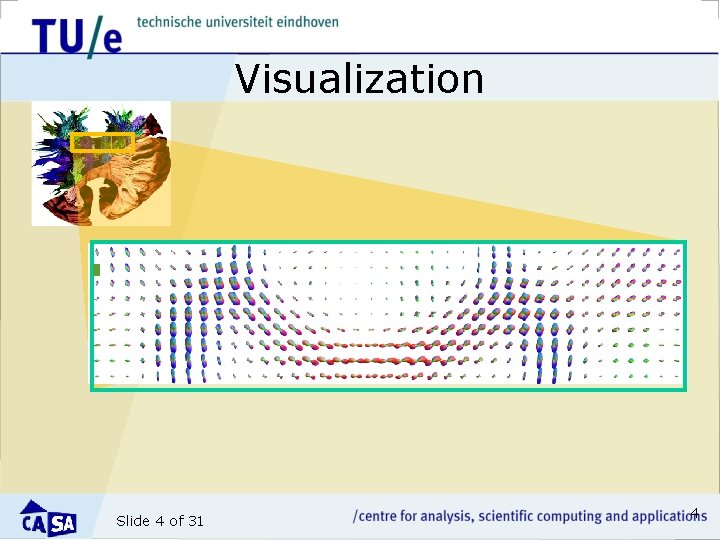
Visualization Slide 4 of 31 4

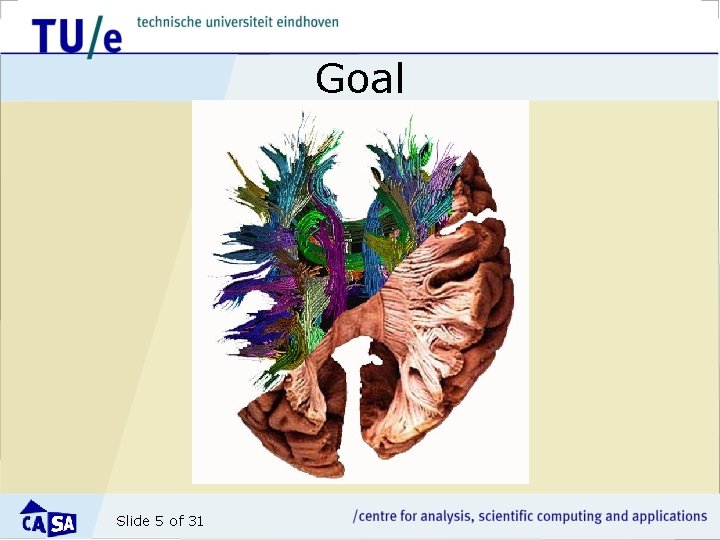
Goal Slide 5 of 31

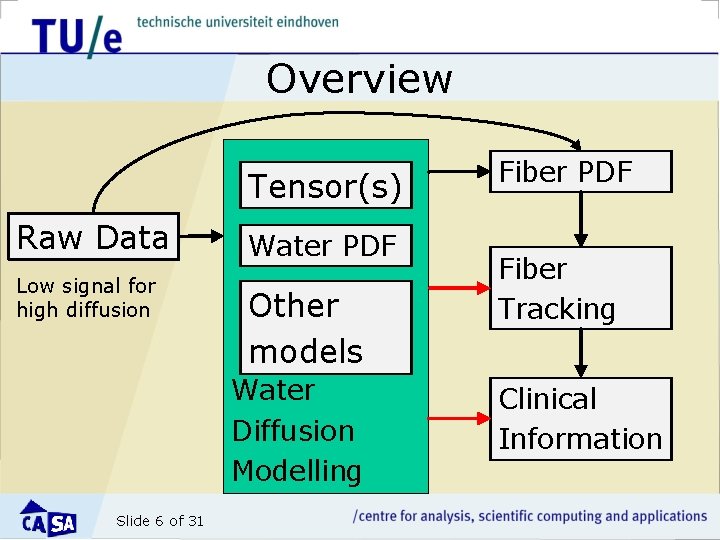
Overview Tensor(s) Raw Data Low signal for high diffusion Water PDF Other models Water Diffusion Modelling Slide 6 of 31 Fiber PDF Fiber Tracking Clinical Information

Constrained Spherical Deconvolution Original data (single fiber) Slide 7 of 31 Spherical Deconvolution Constrained Spherical Deconvolution

Enhancement of PDFs • PDFs contain information on the direction of water diffusion (water PDF) or fiber distribution (fiber PDF) • Many models can be converted to a PDF - Often noisy and incoherent Slide 8 of 31

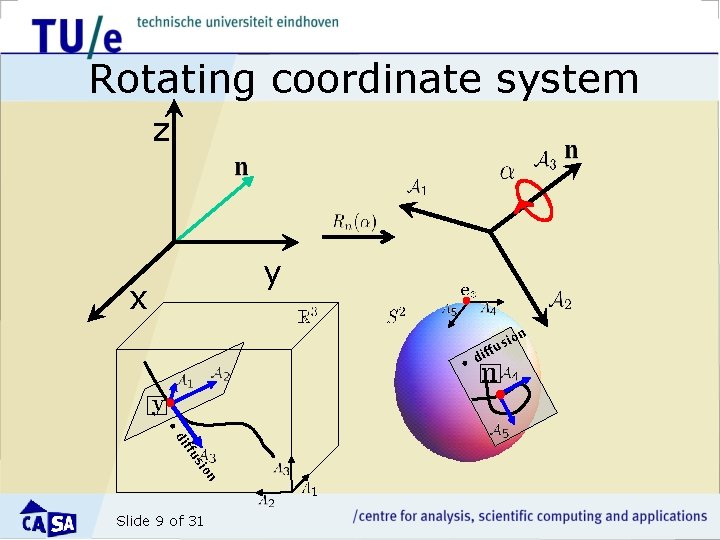
Rotating coordinate system z y x n • • n io us ff di Slide 9 of 31 f dif io us

Evolutions in new frame • Contour Enhancement Slide 10 of 31

Evolutions in new frame • Contour Completion Contour completion Slide 11 of 31

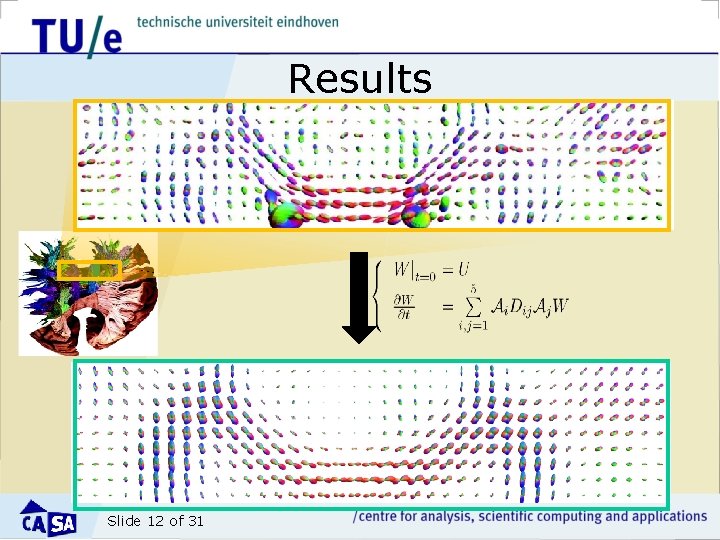
Results Slide 12 of 31

Results on simple fibertracking • Fibertracking on CSD • Fibertracking on enhanced CSD Phantom dataset from the ISBI reconstruction challenge (2013) Slide 13 of 31

Fiber Tracking • Problem: find anatomical fibers based on DW-MRI scan – Variants • Find brain fiber between two areas • Find all fibers that pass through an area • Mathematical problem? – Multiple options Slide 14 of 31

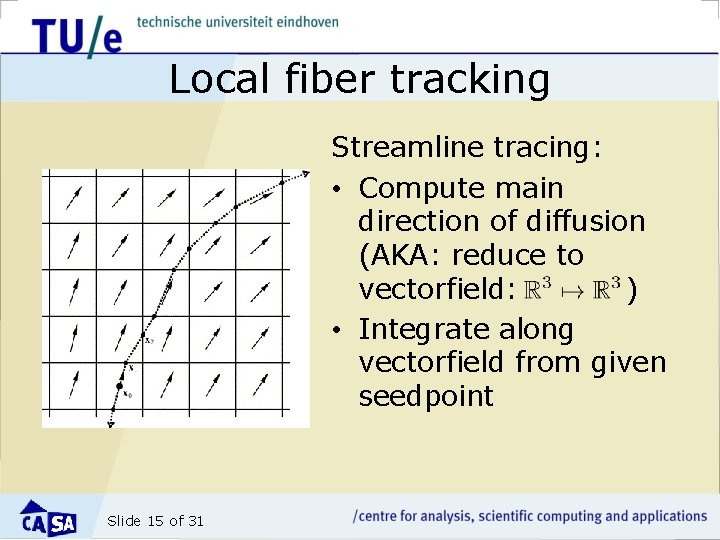
Local fiber tracking Streamline tracing: • Compute main direction of diffusion (AKA: reduce to vectorfield: ) • Integrate along vectorfield from given seedpoint Slide 15 of 31

Advantages/Disadvantages • Advantages – Computationally cheap – Easy to implement • Disadvantages – Error accumulation – Sensitive to noise Slide 16 of 31

Local method: example Slide 17 of 31

Global fibertracking • curve Curvature • Corresponding energy functional Solved for C(x)=1 External cost (data) Geodesic energy • Find for given end points/directions Slide 18 of 31

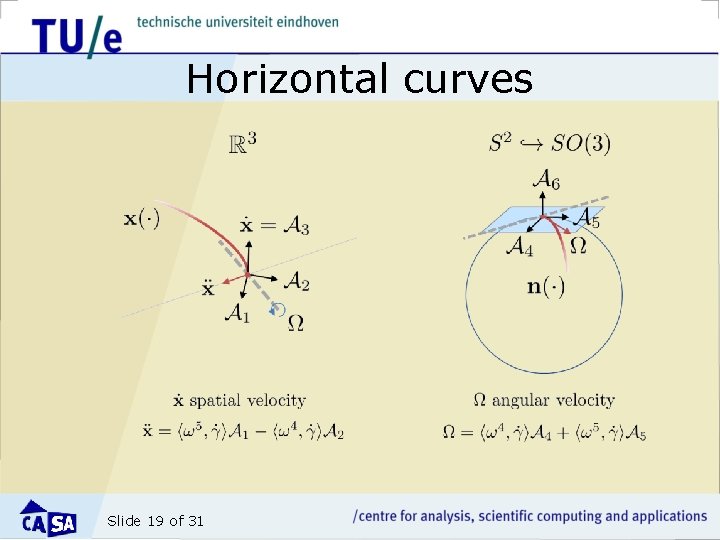
Horizontal curves Slide 19 of 31

Lifting the optimal curve problem to The energy functional to minimize subject to the constraints along the curve: Slide 20 of 31

Solutions sub-Riemannian geodesics Ghosh&Dela Haije&Duits Slide 21 of 31

Optimal control problem Slide 22 of 31

Benefits and disadvantages • Advantages – Robust to noise – No error accumulation • Disadvantages – Computationally expensive – Needs more boundary conditions – Can sacrifice local error for global optimization Slide 23 of 31

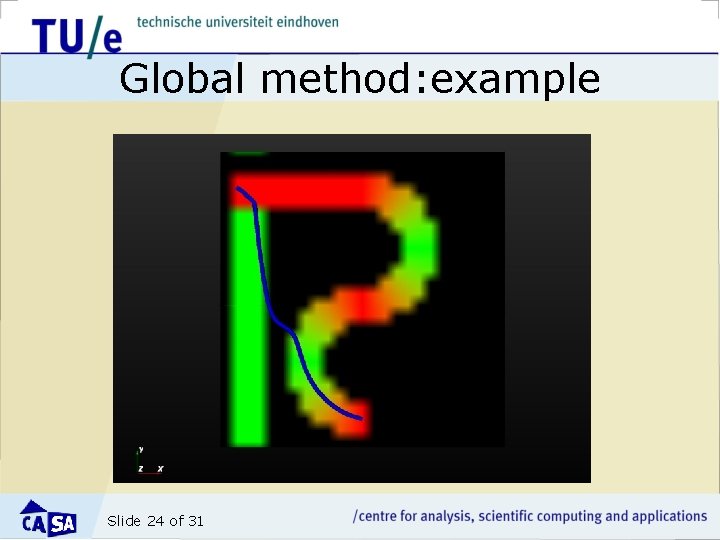
Global method: example Slide 24 of 31

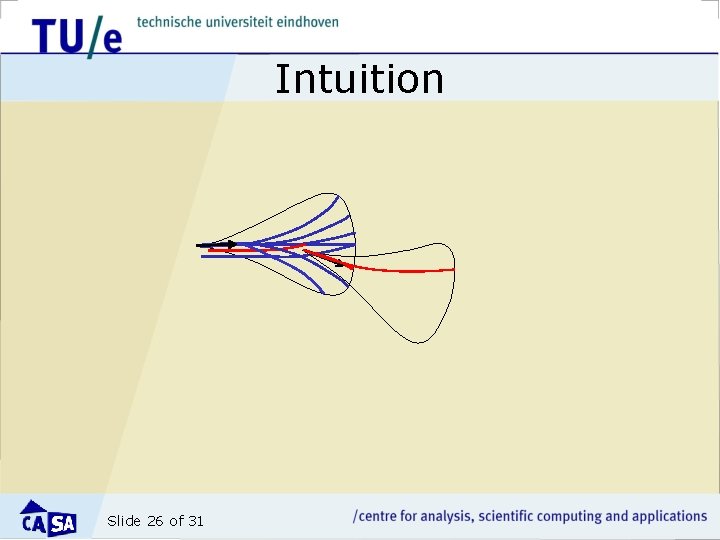
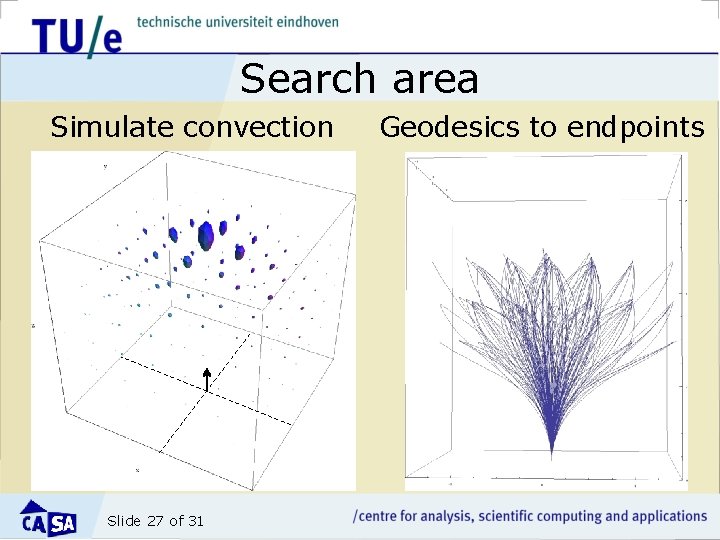
New idea: combine local and global • Not global energy minimizers, but limit search to smaller search areas and combine solutions • Add additional constraints to limit search space – Limit curvature to be below threshold – Do extra constraints change optimal curve problem? Slide 25 of 31

Intuition Slide 26 of 31

Search area Simulate convection Slide 27 of 31 Geodesics to endpoints

Theoretical benefits • Advantages – Robust to noise – Computational intermediate – Balance between local and global error – Limits to local or global method for search area small or large • Disadvantages – Extra parameters that need to be tuned Slide 28 of 31

How to find optimum curve? • Minimizer may not exist • Minimizer may not be unique • Different options – Use Dijkstra to find cheapest path along tree-graph (restricts energy function) – Try discrete subset of curves – Get an approximate minimizer and iteratively refine it Slide 29 of 31

Past and Plans • Article published in NM-TMA (feb ‘ 13) • Enhancement Article published in JIMV • Refine ideas and publish proof-of-concept to MICCAI conference (June) • Expand for journal article • Visit Berlin to work on new non-linear enhancement technique (August) Slide 30 of 31

Any questions, ideas or suggestions? Slide 31 of 31