Analysis and different implementations of shortest path algorithm

Analysis and different implementations of shortest path algorithm Floyd Warshall. Comparison of Floyd Warshall and Dijkstra algorithm Ivan Boškov

Introduction • An optimal shortest-path is one with the minimum length criteria from a source to a destination. • There are various graph types that shortest-path algorithms consider: – Aspatial graph – the position of the vertices is not interpreted as a location in space – Spatial graph – Planar graph – plotted in 2 D with no edges crossing and with continuous edges • The graphs can be divided into: – Static / Dynamic – Directed / undirected edges – Negative / Non-negative weights

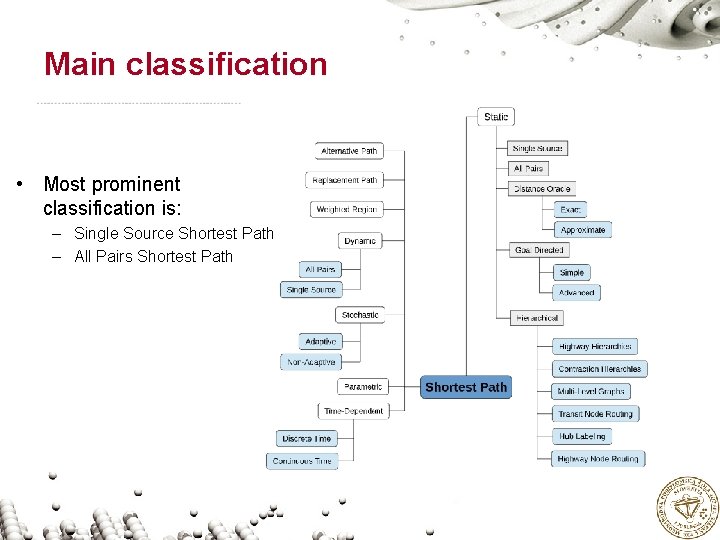
Main classification • Most prominent classification is: – Single Source Shortest Path – All Pairs Shortest Path

Problem Definition • Set of vertices V – Source s, destination d (s, d ∈ V) • Set of edges E over V • Goal: find the shortest path between s and d that has the min weight • Input: Graph G consisting of V and E (G=(V, E)) • Edges can be directed or undirected • The weight is defined as w(e) where e ∈ E

Single Source Shortest Path • Definition: Given a Graph G = (V, E) and source s ∈ V, compute all distances δ(s, v), where v ∈ V • Dijkstra Algorithm: – – – Single Source Shortest Path Find distance from given source to all destinations Used over directed graphs with non-negative weights Time complexity O((V+E)log V) Brute-force search to find the optimum shortest path, greedy algorithm • Dijkstra’s algorithm can be computed separately for each vertex in the graph. – Time complexity O(EV log V), worst case O(V 3 log. V)

Dijkstra Algorithm • 1) Create a set (shortest path tree set) that keeps track of vertices included in shortest path tree. Initially, this set is empty. 2) Initialize all distance values as INFINITE. Assign distance value as 0 for the source vertex so that it is picked first. 3) While the shortest path tree set is not empty a) Pick a vertex s which is not in the shortest path tree set and has minimum distance value. b) Include s to the shortest path tree set. c) Update distance value of all adjacent vertices of s. • • To update the distance values, iterate through all adjacent vertices. For every adjacent vertex v, if sum of distance value of s and weight of edge s -v, is less than the distance value of v, then update the distance value of v.

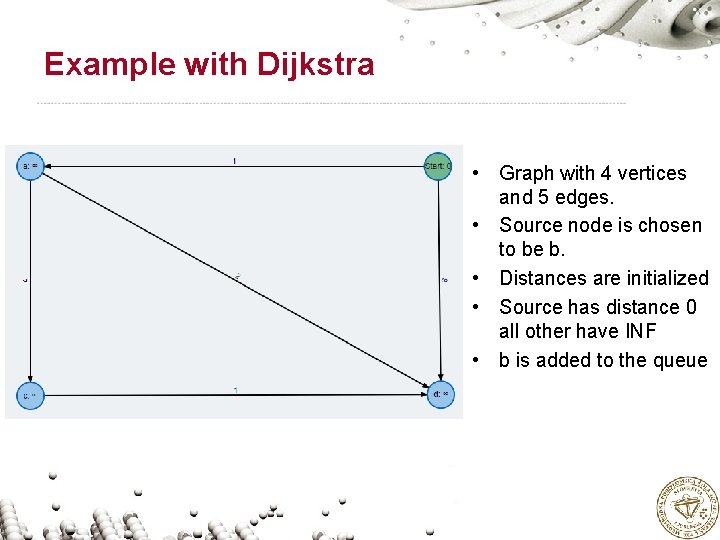
Example with Dijkstra • Graph with 4 vertices and 5 edges. • Source node is chosen to be b. • Distances are initialized • Source has distance 0 all other have INF • b is added to the queue

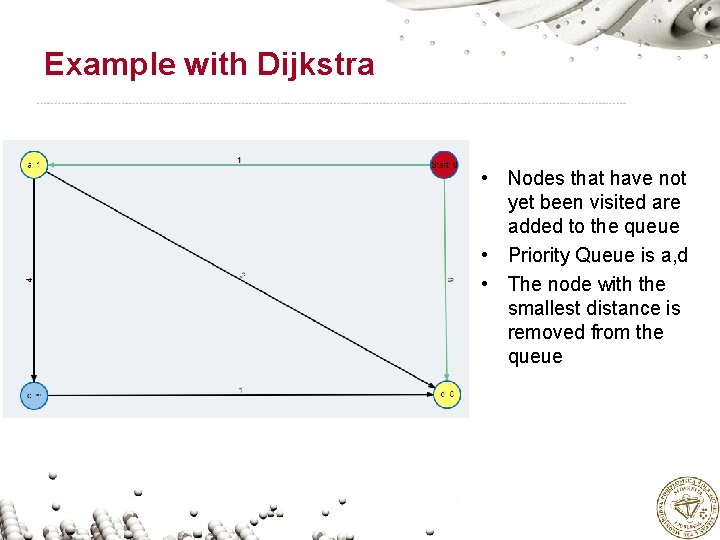
Example with Dijkstra • Nodes that have not yet been visited are added to the queue • Priority Queue is a, d • The node with the smallest distance is removed from the queue

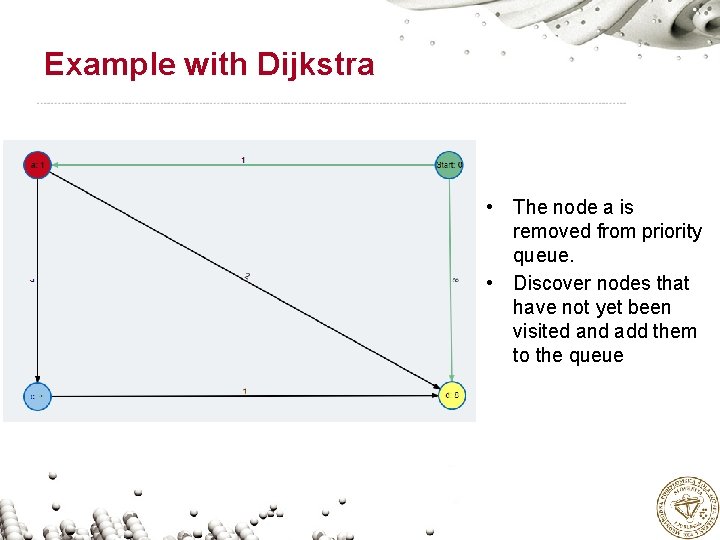
Example with Dijkstra • The node a is removed from priority queue. • Discover nodes that have not yet been visited and add them to the queue

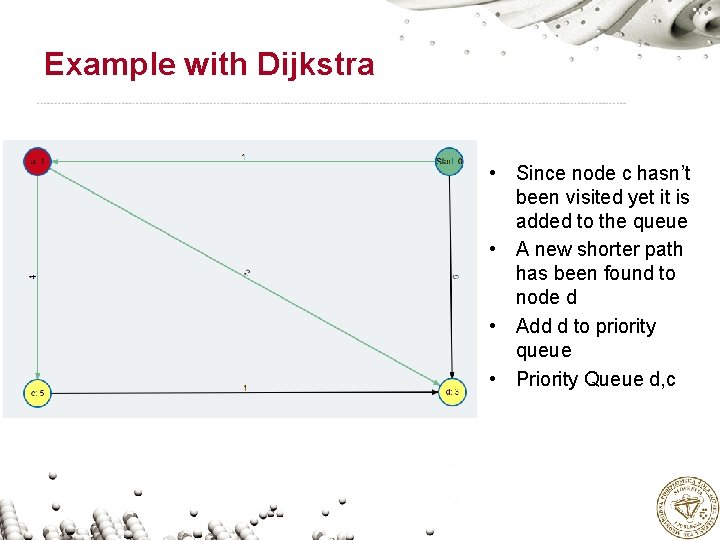
Example with Dijkstra • Since node c hasn’t been visited yet it is added to the queue • A new shorter path has been found to node d • Add d to priority queue • Priority Queue d, c

All Pair Shortest Path • Definition: Given a graph G = (V, E), compute all distances between a source s and destination d where s, d ∈ V • Optimal solution Floyd Warshall Algorithm. • Finds all pairs shortest path in weighted graph with positive and negative weighted edges. • Time complexity is O(V 3).

Floyd Warshall Algorithm • Graph G with vertices V numbered 1 through N. • Consider a function shortest. Path(i, j, k) – returns the shortest path from i to j using vertices only from the set {1, 2, …. , k} as intermediate points along the way. • The goal is to find the shortest path from each i to each j using only vertices in {1, 2, …. , N}. • For each pair of vertices, the shortest. Path(i, j, k) could be either – a path that does not go through k (only uses vertices in the set {1, …. , k-1}. ) – a path that does go through k (from i to k and then from k to j, both only using intermediate vertices in {1, …. , k-1})

Floyd Warshall Algorithm • The best path from i to j that only uses vertices 1 through k-1 is defined by shortest. Path(i, j, k-1) • if there were a better path from i to k to j – the length of the path would be the concatenation of the shortest path from i to k and the shortest path from k to j. • If w(i, j) is the weight of the edge between vertices i and j – the base case is – the recursive case is

Implementation of Floyd Warshall

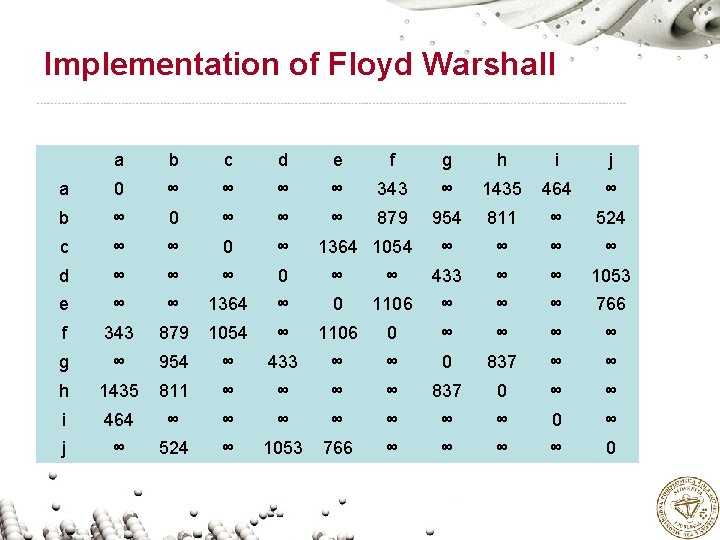
Implementation of Floyd Warshall a b c d e f g h i j a 0 ∞ ∞ 343 ∞ 1435 464 ∞ b ∞ 0 ∞ ∞ ∞ 879 954 811 ∞ 524 c ∞ ∞ 0 ∞ ∞ ∞ d ∞ ∞ ∞ 0 ∞ ∞ 433 ∞ ∞ 1053 e ∞ ∞ 1364 ∞ 0 1106 ∞ ∞ ∞ 766 f 343 879 1054 ∞ 1106 0 ∞ ∞ g ∞ 954 ∞ 433 ∞ ∞ 0 837 ∞ ∞ h 1435 811 ∞ ∞ 837 0 ∞ ∞ i 464 ∞ ∞ ∞ ∞ 0 ∞ j ∞ 524 ∞ 1053 766 ∞ ∞ 0 1364 1054

Implementation of Floyd Warshall Add all vertices one by one to the set of intermediate vertices. Before start of an iteration, we have shortest distances between all pairs of vertices such that the shortest distances consider only the vertices in set {0, 1, 2, . . k-1} as intermediate vertices. After the end of an iteration, vertex no. k is added to the set of intermediate vertices and the set becomes {0, 1, 2, . . k} for (k = 0; k < V; k++) { for (i = 0; i < V; i++) { for (j = 0; j < V; j++) { if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } }

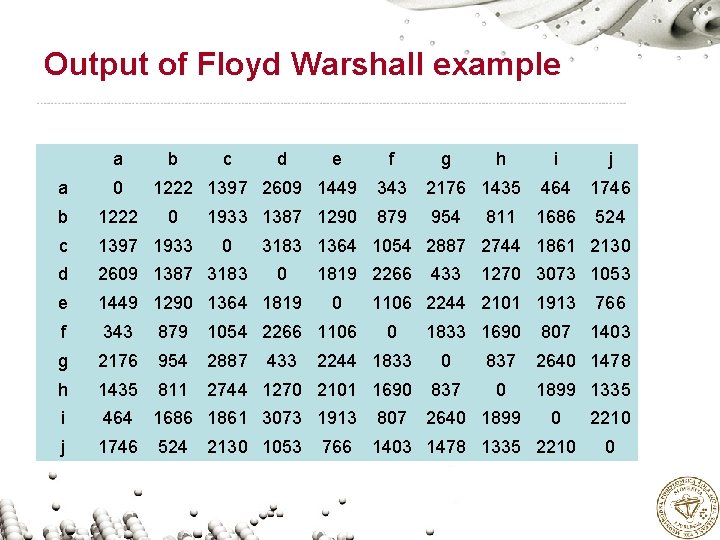
Output of Floyd Warshall example a b c d e 1222 1397 2609 1449 f g h i j a 0 b 1222 c 1397 1933 d 2609 1387 3183 e 1449 1290 1364 1819 f 343 879 1054 2266 1106 g 2176 954 2887 h 1435 811 2744 1270 2101 1690 i 464 1686 1861 3073 1913 807 j 1746 524 1403 1478 1335 2210 0 1933 1387 1290 0 343 2176 1435 464 1746 879 954 1686 524 811 3183 1364 1054 2887 2744 1861 2130 0 433 2130 1053 1819 2266 0 1270 3073 1053 1106 2244 2101 1913 0 2244 1833 766 433 1833 1690 807 766 1403 0 837 2640 1478 837 0 1899 1335 2640 1899 0 2210 0

Conclusion • • • Main Purposes: Dijkstra’s Algorithm is one example of a single-source shortest or SSSP algorithm, i. e. , given a source vertex it finds shortest path from source to all other vertices. Floyd Warshall Algorithm is an example of all-pairs shortest path algorithm, meaning it computes the shortest path between all pair of nodes. Time Complexities : Time Complexity of Dijkstra’s Algorithm: O((V+E)log V) Time Complexity of Floyd Warshall: O(V 3) Other Points: We can use Dijskstra’s shortest path algorithm for finding all pair shortest paths by running it for every vertex. But time complexity of this would be O(VE Log V) which can go (V 3 Log V) in worst case. Another important differentiating factor between the algorithms is their working towards distributed systems. Unlike Dijkstra’s algorithm, Floyd Warshall can be implemented in a distributed system, making it suitable for data structures such as Graph of Graphs (Used in Maps). Lastly Floyd Warshall works for negative edge but no negative cycle, whereas Dijkstra’s algorithm doesn’t work for negative edges.