Analyse tempsfrquence Spectrogramme Distribution de Wigner Ville SY

Analyse temps-fréquence Spectrogramme Distribution de Wigner Ville SY 16 -Traitement du signal : Analyse temps fréquence 1

Les signaux non stationnaires • Un signal dont la ‘ structure ’ change au cours du temps – parole, musique, impacts, ‘ chirp ’, machines tournantes lors d ’accélération ou décélération, – on souhaite faire l ’analyse en fréquence de régions locales du signal. i. e. localisée temporellement. • ANALYSE TEMPS FREQUENCE • Une limite « le principe d’incertitude » – B largeur de bande fréquentiel d ’un signal, – T durée du signal • alors : BT 1/2 – plus on veut se localiser sur une portion d ’un signal – moins on peut spécifier les fréquences précisément SY 16 -Traitement du signal : Analyse temps fréquence 2

Le spectrogramme formulation • DSP x(t) signal stationnaire x(t) – x (f) = x(t). e-2 jft 2 est indépendant du temps • Spectrogramme : non stationnaire = suite de non stationnarités – Sx (t, f) = x(u). h(u-t). e-2 jft 2 est fonction du temps et de la fréquence – h(t) est une fenêtre glissante • bonne résolution temporelle si h(t) courte • bonne résolution fréquentielle si h(t) longue SY 16 -Traitement du signal : Analyse temps fréquence 3

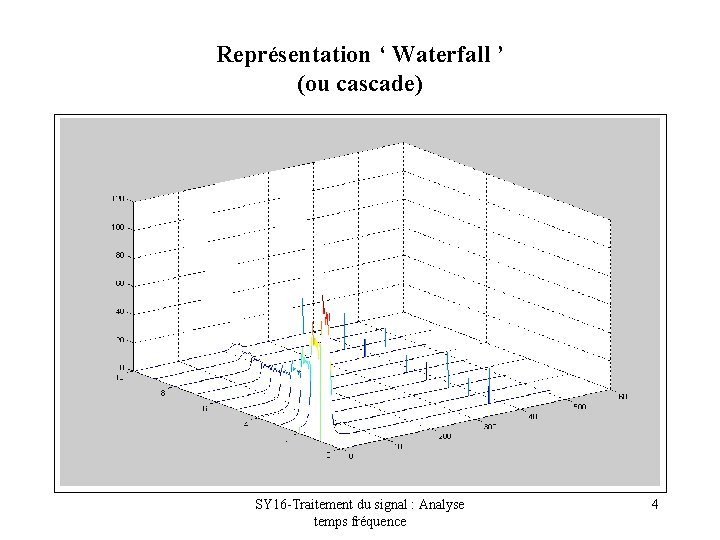
Représentation ‘ Waterfall ’ (ou cascade) SY 16 -Traitement du signal : Analyse temps fréquence 4

Le spectrogramme Représentation plan SY 16 -Traitement du signal : Analyse temps fréquence 5

Le spectrogramme quelques propriétés • Les plus: – positif, – extension directe de Fourier, interprétation identique en fréquences – pas de termes d ’interférences • Les moins: – principe d ’incertitude BT 1/2, • compromis entre résolutions en fréquence et en temps – la résolution et les lois en fréquence sont fonction de la fenêtre – l ’optimisation des fenêtres nécessite des informations a priori sur le signal SY 16 -Traitement du signal : Analyse temps fréquence 6

Spectrogramme: chirp nfft=64 SY 16 -Traitement du signal : Analyse temps fréquence 7

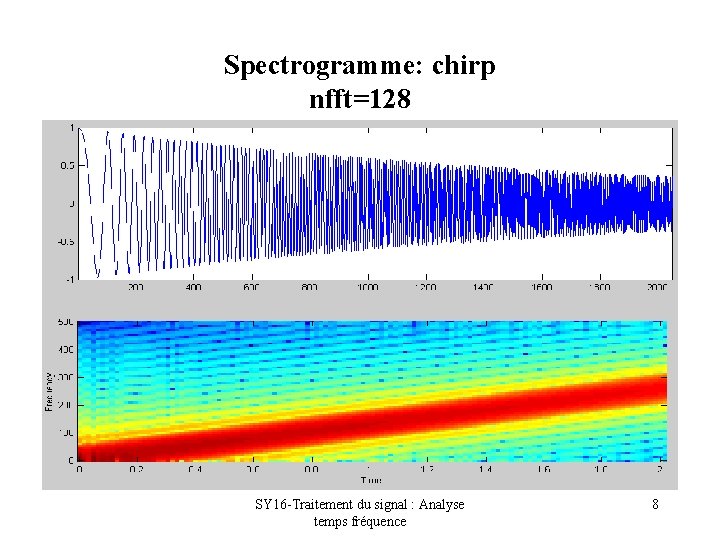
Spectrogramme: chirp nfft=128 SY 16 -Traitement du signal : Analyse temps fréquence 8

Spectrogramme chirp nfft=256 SY 16 -Traitement du signal : Analyse temps fréquence 9

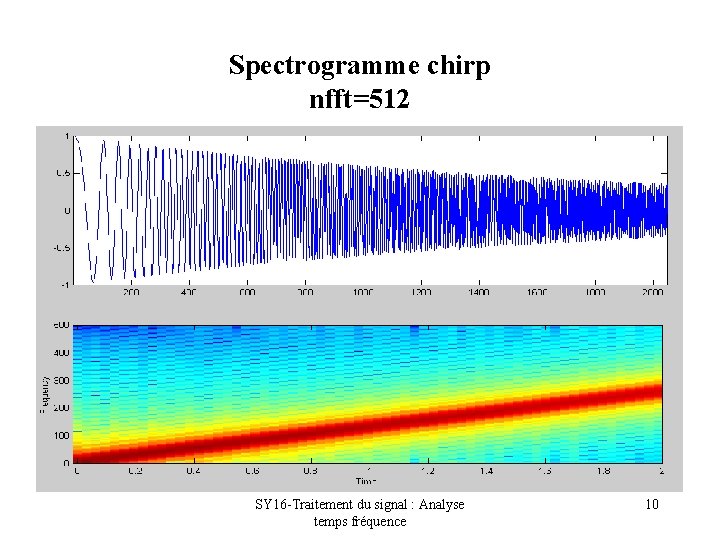
Spectrogramme chirp nfft=512 SY 16 -Traitement du signal : Analyse temps fréquence 10

Spectrogramme: double chirp (nfft=128) SY 16 -Traitement du signal : Analyse temps fréquence 11

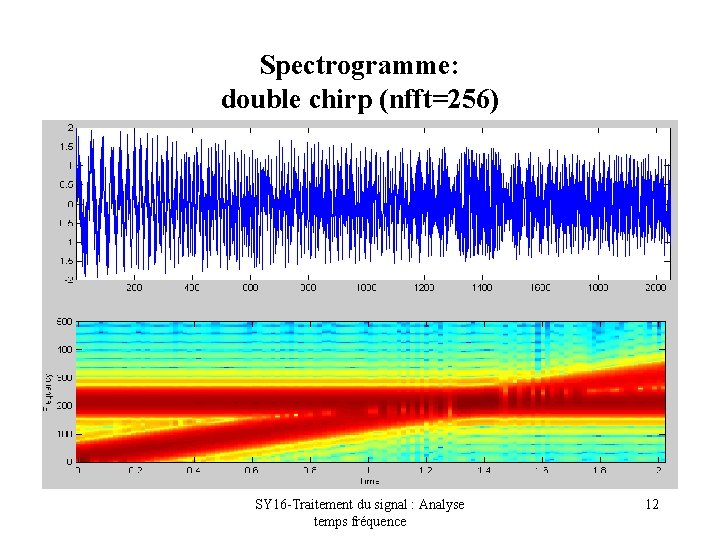
Spectrogramme: double chirp (nfft=256) SY 16 -Traitement du signal : Analyse temps fréquence 12

Spectrogramme: double chirp (nfft=512) SY 16 -Traitement du signal : Analyse temps fréquence 13

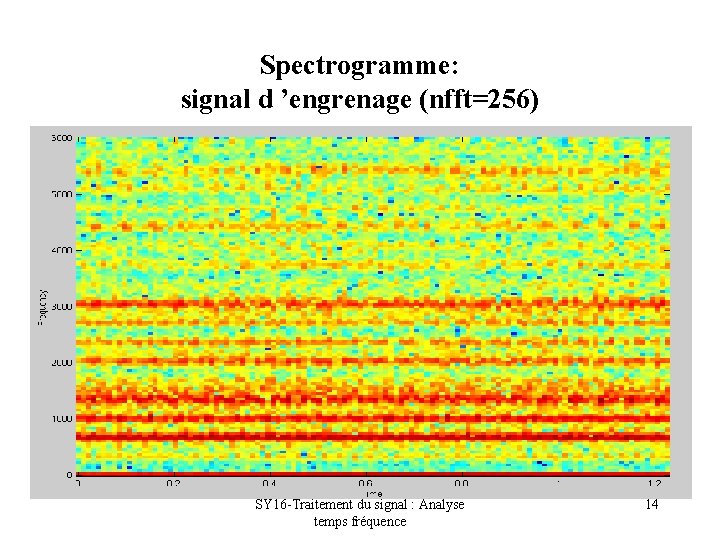
Spectrogramme: signal d ’engrenage (nfft=256) SY 16 -Traitement du signal : Analyse temps fréquence 14

Spectrogramme: signal d ’engrenage (nfft=1024) SY 16 -Traitement du signal : Analyse temps fréquence 15

Comment définir une fréquence ? • Dans le cas stationnaire – Fourier – « Sinusoïde de durée infinie » • Dans le cas non stationnaire – même définition que le cas stationnaire mais QUI VARIE DANS LE TEMPS? ? • Impossible à cause du principe d’incertitude – On définit alors la FREQUENCE INSTANTANEE • signal analytique, – cette quantité est fonction du temps, elle correspond à la sinusoïde qui suit au mieux le signal – cependant elle est adaptée à un signal à bande étroite (. i. e. une composante) SY 16 -Traitement du signal : Analyse temps fréquence 16

Fréquence instantanée et retard de groupe pour un signal monochromatique • Fréquence instantanée • x(t) = cos (2. . f 0. t) • xa(t) = cos (2. . f 0. t) + j. sin (2. . f 0. t) = e 2. j. . f 0. t • fi (t) = 1/2. d/dt { arg (xa(t) } = f 0 – localisation en fréquence d ’une composante temporelle • Retard de groupe • Xa(f) = TF { xa(t) } • tg = 1/2. d/df { Arg Xa(f) } retard de groupe • x(t) = cos (2. . f 0. t), xa(t) = e 2. . f 0. t – Xa(f) = (f-f 0) tg=0 • x(t) = cos (2. . f 0. (t-t 0)), xa(t) = e 2. . f 0. (t-t 0) – Xa(f)= (f-f 0). e-2 . j f 0 t 0 tg=t 0 – localisation en temps d ’une composante fréquentielle SY 16 -Traitement du signal : Analyse temps fréquence 17

Distributions temps fréquence • Objectifs: – Améliorer la résolution en temps et en fréquence de l ’analyse d ’un signal non stationnaire • Des représentations temps- fréquence ont été développées pour avoir la meilleure répartition de l ’énergie dans ce plan. • Ces représentations sont dites représentations quadratiques – Distribution de Wigner, – Classe générale de Cohen – d ’autres représentations existent (Choï Williams, . . ) SY 16 -Traitement du signal : Analyse temps fréquence 18

Quelles sont les propriétés souhaitées pour une représentation T-F ? ? SY 16 -Traitement du signal : Analyse temps fréquence 19

Fréquence instantanée et retard de groupe pour un chirp • Chirp (sinus à balayage linéaire d ’amplitude constante (durée infinie) – x(t) = a. cos ( 2 (t)) = a. cos(2 (f 0 t + b/2. t 2)) – xa(t) = a. e 2 j(f 0 t + b/2. t^2), Xa(t) = A(f) e j (t) • fréquence instantanée f(t) = (1/2 ). d (t)/dt = f 0+b/2. t • retard de groupe tg(f)= (1/2 ). d (t)/df = -2/b. (f-f 0) – réciprocité entre la fréquence instantanée et le retard de groupe • Ces notions sont importantes – pour les signaux mono composantes – pour les signaux dont l ’amplitude varie lentement vis-à-vis de la fréquence la plus basse • Dans les autres cas, la fréquence instantanée sera une valeur moyenne SY 16 -Traitement du signal : Analyse temps fréquence 20

La fonction d’autocorrélation et DSP • Aléatoire stationnaire • Aléatoire , non stationnaire SY 16 -Traitement du signal : Analyse temps fréquence 21

La fonction d’autocorrélation signal déterministe • Ecriture de la fonction d ’autocorrélation • Déterministe SY 16 -Traitement du signal : Analyse temps fréquence 22

Spectre de Wigner Ville : définition • Pour un signal déterministe • Cas particulier : • On obtient la transformation de Wigner Ville SY 16 -Traitement du signal : Analyse temps fréquence 23

Distribution de Wigner Ville • Signaux déterministes Signaux aléatoires • Rem: la représentation de Wigner Ville prend en compte TOUT le signal. • Pour les signaux déterministes => Représentation de WV • Pour les signaux aléatoires => Spectre de WV SY 16 -Traitement du signal : Analyse temps fréquence 24

Propriétés de la TF de Wigner Ville (1) SY 16 -Traitement du signal : Analyse temps fréquence 25

Propriétés de la TF de Wigner Ville (2) • Inconvénients – Valeurs négatives locales !!! – Interférences entre les composantes des signaux • ceci est du au produit x(t-T/2) x(t+T/2) • Avantages – – meilleure résolution en temps et fréquence puisque on utilise tout le signal propriétés marginales estimation des modulations de fréquences du retard de groupe SY 16 -Traitement du signal : Analyse temps fréquence 26

Wigner Ville cas discret – l ’indice l, dans la TFWV directe correspond à l. t/2 – l ’indice k, dans la TFWV inverse correspond à k/2. M. t • D ’où un échantillonnage 2 fois plus fin! • Autre interprétation: • le produit des 2 signaux x(t), x(t+T/2) donne dans le domaine fréquentiel une convolution avec un spectre de largeur double! D ’où la nécessité d ’échantillonner à une fréquence double de celle de Nyquist! SY 16 -Traitement du signal : Analyse temps fréquence 27

Transformée de Wigner Ville Utilisation du signal analytique • Au lieu d ’utiliser x(t), on utilise souvent le signal analytique de x(t) • • Ce signal a un spectre défini uniquement pour les fréquences positives. Ce permet: – d ’éviter d ’échantillonner à la fréquence double! – d ’éviter les interactions entre les fréquences positives et négatives du spectres. • Formulation basée sur la TF des signaux • remarque: – il n ’y a pas de pertes d ’informations – WV est défini pour les fréquences positives, sans pertes d ’informations SY 16 -Traitement du signal : Analyse temps fréquence 28

Pseudo Wigner-Ville et Pseudo Wigner-Ville Lissé • Pseudo Wigner Ville : lissage en fréquence – version lissée en fréquence – on utilise une portion du signal – moins bonne résolution en fréquence • Pseudo Wigner Ville Lissé : lissage en temps et fréquence – – convolution bi-dimensionnelle réduction des interférences positivité perte de résolution T-F SY 16 -Traitement du signal : Analyse temps fréquence 29

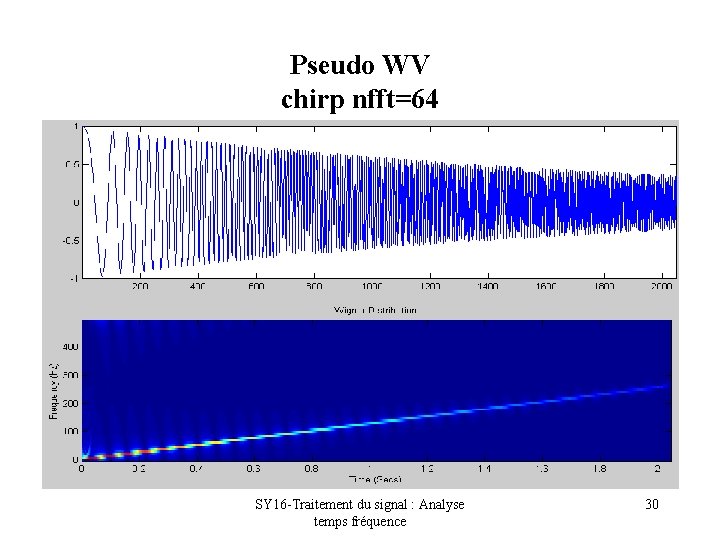
Pseudo WV chirp nfft=64 SY 16 -Traitement du signal : Analyse temps fréquence 30

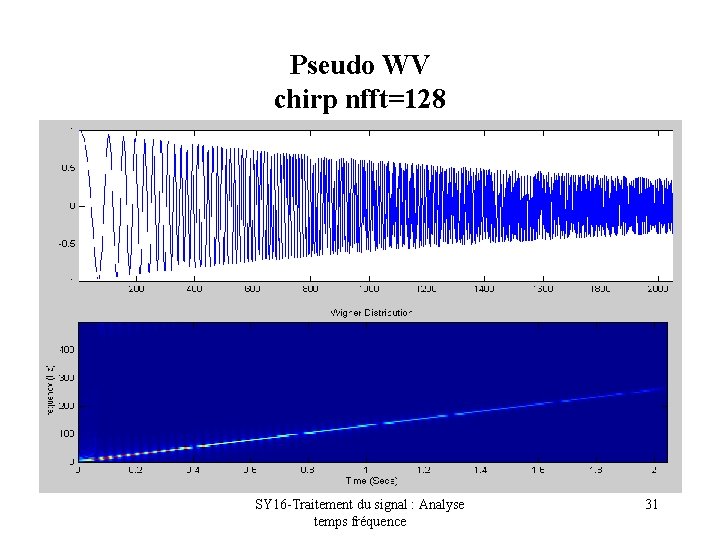
Pseudo WV chirp nfft=128 SY 16 -Traitement du signal : Analyse temps fréquence 31

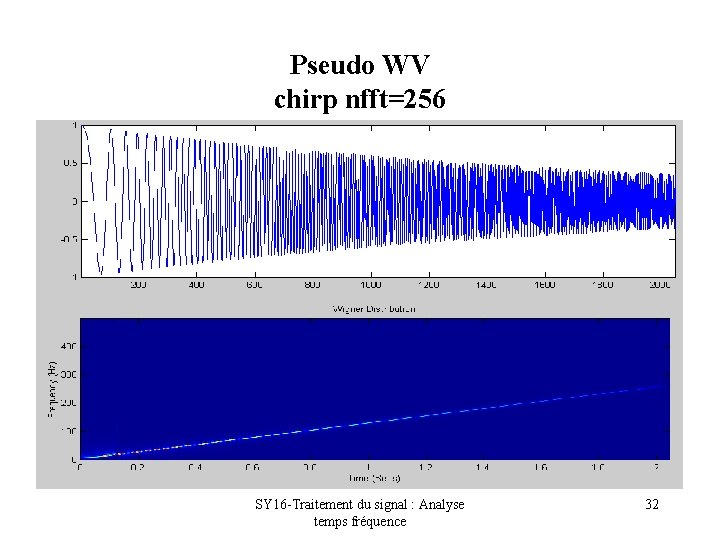
Pseudo WV chirp nfft=256 SY 16 -Traitement du signal : Analyse temps fréquence 32

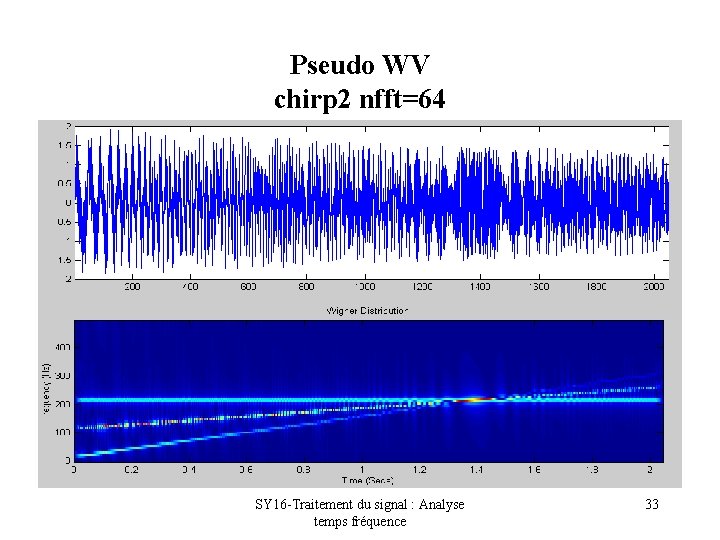
Pseudo WV chirp 2 nfft=64 SY 16 -Traitement du signal : Analyse temps fréquence 33

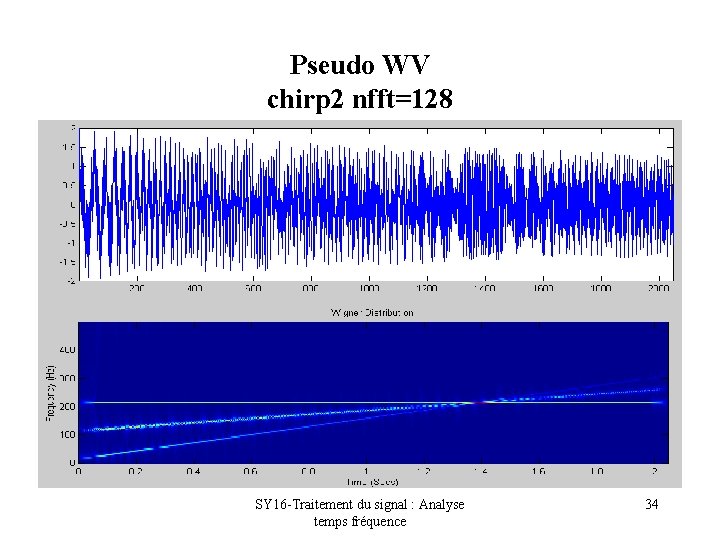
Pseudo WV chirp 2 nfft=128 SY 16 -Traitement du signal : Analyse temps fréquence 34

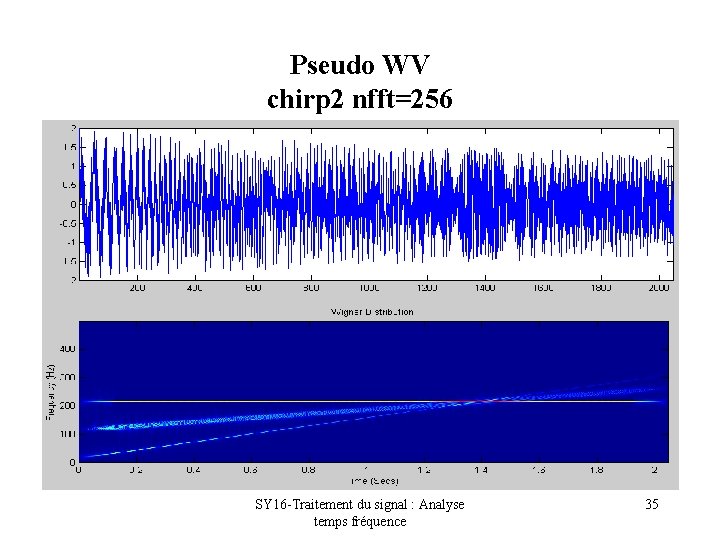
Pseudo WV chirp 2 nfft=256 SY 16 -Traitement du signal : Analyse temps fréquence 35

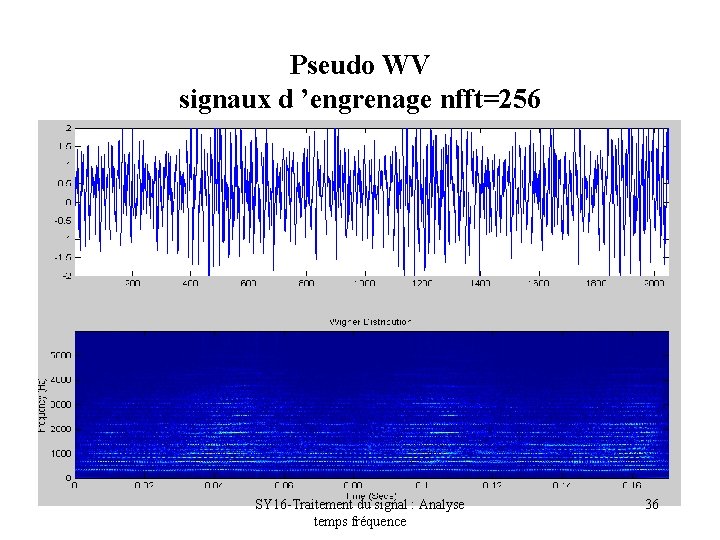
Pseudo WV signaux d ’engrenage nfft=256 SY 16 -Traitement du signal : Analyse temps fréquence 36

Pseudo Xigner Ville Lissé et Spectrogramme • Spectrogramme WV du signal WV de la fenêtre • Interprétation: – le spectrogramme correspond à une version lissée du spectrogramme SY 16 -Traitement du signal : Analyse temps fréquence 37

Annexe : représentation générale des représentations quadratiques La classe de Cohen • SY 16 -Traitement du signal : Analyse temps fréquence 38

Cas particuliers de la classe de Cohen • Forme générale SY 16 -Traitement du signal : Analyse temps fréquence 39