Analyse de la rgression linaire Lanalyse de la

Analyse de la régression linéaire. L’analyse de la régression a pour objet l’étude de la valeur moyenne d’une variable Y, appelée variable à expliquer ou variable dépendante, lorsqu’une ou plusieurs autres variables, appelées variables indépendantes ou variables explicatives (notées généralement X 1, X 2, …. ) sont maintenues à des niveaux fixes (x 1, x 2, …. ).

Le modèle mathématique n n La valeur moyenne (Y| X 1=x 1, X 2=x 2, …. ) de Y lorsque X 1=x 1, X 2=x 2, …. est une fonction de x 1, x 2, …. En théorie (Y| X 1=x 1, X 2=x 2, …. ) peut avoir n’importe quelle forme mathématique mais on ne sait traiter correctement que le cas linéaire ; c’est-à-dire quand (Y| X 1=x 1, X 2=x 2, …. ) = 0+ 1 x 1+ 2 x 2+…

suite n n Dans la pratique on ne peut observer (Y| X 1=x 1, X 2=x 2, …. ) mais des réalisations particulières y 1, y 2, …. , yn de la variable dépendante Y. Ce qui fait on écrit yi = (Y| X 1=x 1, X 2=x 2, …. ) + i i=1, …, n où n représente le nombre d’observations.

Régression linéaire simple n Quand il n’y a qu’une seule variable explicative et qu’on suppose une relation linéaire simple entre Y et X on écrit yi = 0 + 1 xi+ i ; i = 1, …, n i ~variables aléatoires i. i. d. de loi N(0, 2). Les termes i représentent les erreurs.

Questions n n n La variable Y n’est pas influencée par la variable indépendante X, H 0 : 1 = 0. Comment estimer les paramètres du modèle 0, 1 ? Vérification des hypothèses théoriques

Estimation des paramètres n Elle se fait en minimisant la somme des carrés des erreurs , c’est-à-dire en minimisant l’expression i 2 = ( yi - 0 - 1 x i ) 2 La solution de ce problème est : = a 1 = et

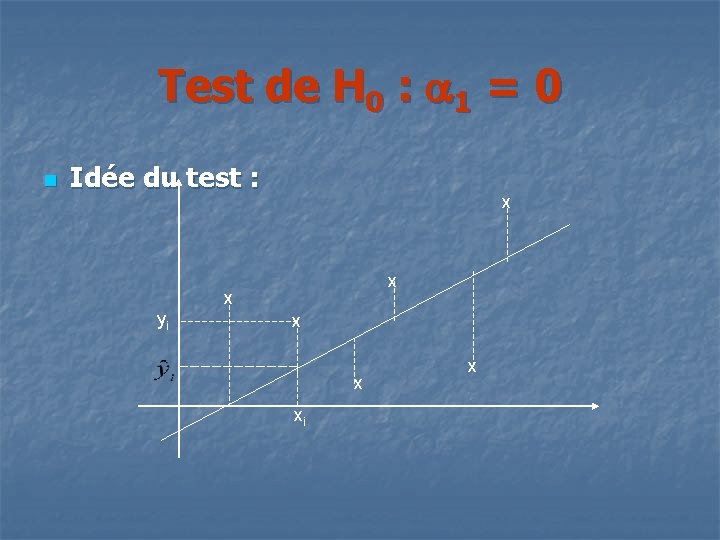
Test de H 0 : 1 = 0 n Idée du test : x x x yi x x xi x

Somme des carrés des écarts n S. C. E. Totale = n S. C. E. résiduelle = n S. C. E. régression = n De plus, on a S. C. E. Totale = S. C. E. régression + S. C. E. résiduelle

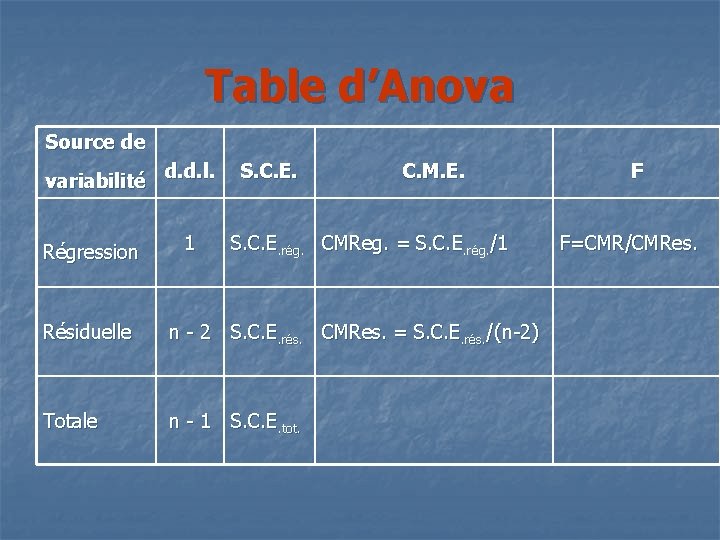
Table d’Anova Source de variabilité d. d. l. Régression 1 S. C. E. C. M. E. S. C. E. rég. CMReg. = S. C. E. rég. /1 Résiduelle n - 2 S. C. E. rés. CMRes. = S. C. E. rés. /(n-2) Totale n - 1 S. C. E. tot. F F=CMR/CMRes.

Règle de décision n n La régression est significative si Ftable d’ANOVA > C (lu dans la table de loi F de Fisher Snedecor) Ou encore plus simplement « Rejeter H 0 si a > p-value »

Interprétation n Que veut dire « régression significative » ? La variable X explique de façon significative les variations observées sur la variable Y.

Discussion des conditions théoriques du modèle. n On appelle résidu la quantité e i = yi – Résidu standardisé eistd = Normalité : la majorité des résidus standardisés doivent se trouver dans l’intervalle [-2, 2].

Suite n Indépendance. n Homoscédasticité. n Linéarité.