Analog Digital Signals Prof Aiman Hanna Department of

Analog & Digital Signals © Prof. Aiman Hanna Department of Computer Science Concordia University Montreal, Canada

A nalog & Digital Signals Figure 3. 1 – Digital & Analog Signals 2

D igital Encoding Schemes There are 10 types of people; those who know binary and those who do not. u Digital data are represented by a sequence of 1 s & 0 s u 1 refer to a high electrical voltage, and 0 refers to a low electrical voltage u Two major digital encoding schemes exist: • Non. Return to Zero (NRZ) Encoding • Manchester Encoding 3

D igital Encoding Schemes (continue. . . ) NRZ Encoding u A 0 voltage is transmitted by raising the voltage level high, while 1 is transmitted by using a low voltage Figure 3. 2(a) – NRZ Encoding 4

D igital Encoding Schemes (continue. . . ) NRZI Encoding u An alternative to NRZ is NRZI (Inverted) u The voltage changes only when a 1 is to be sent Figure 3. 2(b) – NRZI Encoding 5

D igital Encoding Schemes u u (continue. . . ) Both NRZ and NRZI have problems; for example what is the exact sequence being transmitted in the sequence below? Is time synchronization possible? Figure 3. 3 – NRZ Encoding of a Sequence of 0 s 6

D igital Encoding Schemes (continue. . . ) Manchester Encoding u Also called Self-Synchronizing Code u Uses signal changes to keep the sending and receiving devices synchronized u 0 is represented by a change from high to low in the middle of transmission and 1 is represented by a low to high change in the middle of transmission u Are there any disadvantages? Figure 3. 4 – Manchester Encoding 7

D igital Encoding Schemes (continue. . . ) Differential Manchester Encoding u u Similar to Manchester encoding, the signal will change in the middle, however 1 causes the signal to remain the same, while 0 causes the signal to change Figure 3. 5 – Differential Manchester Encoding 8

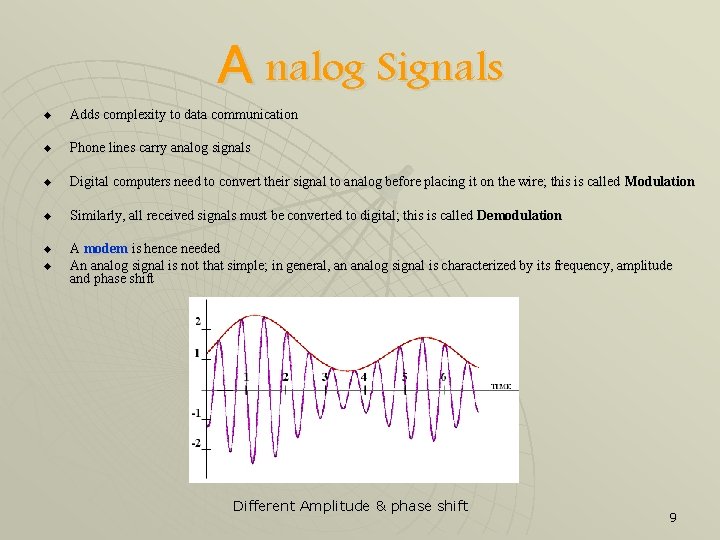
A nalog Signals u Adds complexity to data communication u Phone lines carry analog signals u Digital computers need to convert their signal to analog before placing it on the wire; this is called Modulation u Similarly, all received signals must be converted to digital; this is called Demodulation u u A modem is hence needed An analog signal is not that simple; in general, an analog signal is characterized by its frequency, amplitude and phase shift Different Amplitude & phase shift 9

B it Rate u Describes a medium capacity; that is how many bits can be transferred per unit of time u Measured as Bits Per Second (bps) u A higher bandwidth medium is capable of a higher bit rate u u Transmitter sends a signal representing a bit sting (a component) , while the receiver listens to the medium and creates a bit string based on what it receives Once the component is sent, the transmitter gets another bit string (another component) and the process repeats Figure 3. 9 – Sending Data via Signals 10

B it Rate (continue. . . ) The Nyquist Theorem & Noiseless Channels u u Baud Rate: the frequency with which components change Each bit string is composed of n bits, and hence the signal component may n have up to 2 different amplitudes (one for each unique combination for b 1, b 2, …bn) Are bit rate and baud rate the Same? No, bit rate depends on the number of bits (n) as well as the baud rate; more precisely: Bit Rate = n * Baud Rate u Bit rate can then be increased by either increasing the baud rate or n; however only up to a point 11

B it Rate (continue. . . ) Bit Rate = n * Baud Rate u u u This result is surprisingly old, back to 1920 s, when Harry Nyquist developed his classic theory Nyquist theory showed that if f is the maximum frequency a medium can transmit, then the receiver can reconstruct the signal by sampling it 2 f times per second In other words, the receiver can construct the signal by sampling it at intervals of 1 / 2 f seconds, or twice each period (one period is 1 / f ). For example, if the maximum frequency is 4000 Hz, then the receiver can completely construct it by sampling it every 1/8000 th of a second Assuming that the transmitter baud rate is 2 f , in other words changes signal each 1 / 2 f intervals, we can state Bit Rate = n * Baud Rate = n * 2 * f u This can also be stated based on component; if B is the number of different components, then n B=2 Or u Hence, n = log 2(B) Bit Rate = 2 * f * log 2(B) 12

B it Rate (continue. . . ) Noisy Channels We interject that Nyquist theory assumed that there is absolutely no noise in the channel to alter the signal The result of Nyquist Theorem for a maximum frequency of 3300 Hz, the approximate upper limit of the telephone system, can then be summarized as follows: u u Result of Nyquist Theorem for a maximum of 3300 Hz u N, number of bits B, number of signal components Maximum bit rate (bps) 1 2 6, 600 2 4 13, 200 3 8 19, 800 4 16 26, 400 This result seem to imply that there is no upper bound for a bit rate given the maximum frequency; unfortunately this is not the case due to two main reasons: 1. 2. More components mean subtler change among them Channels are subject to noise 13

Noisy Channels B it Rate (continue. . . ) 1. More components mean subtler change among them 2. Channels are subject to noise u The transmitted signal can be distorted due to the channel noise u If distortion is too large, the receiver may not be able to reconstruct the signal at all Figure 3. 10 – Effect on Noise on Digital Signals (The same applies to analog signals) 14

B it Rate (continue. . . ) Shannon’s Result u u How much noise is bad? This depends on its ratio to the signal We define S/N (Signal-to-Noise-Ratio) A higher S/N (less significant noise) indicates higher quality Because S >> N, the ratio is often scaled down as R = log 10(S/N) bels // bels is the measurement unit For example, If S is 10 times larger than N, then R = log 10(10 N/N) = 1 bel If S is 100 times larger than N, then R = log 10(100 N/N) = 2 bels Perhaps, a more familiar measurement is the decibel (d. B) 1 d. B = 0. 1 bel 15

B it Rate (continue. . . ) Shannon’s Result u u In 1940, Claude Shannon went beyond Nyquist’s results and considered noisy channels Shannon related the maximum bit rate not only to the frequency but also to the S/N ratio; specifically he showed that: Bit Rate = Bandwidth * log 2(1 + S/N) bps u u The formula states that a higher BW and S/N ratio allow higher bit rate Hence, for the telephone system, which has a frequency of about 3000 Hz and S/N ≈ 35 d. B, or 3. 5 bels, Shannon’s result yields the following 3. 5 = log 10(S/N) S = 103. 5 N S ≈ 3162 N S/N ≈ 3162 Bit Rate = Bandwidth * log 2(1 + S/N) = 3000 * log 2(1 + 3162) ≈ 3000 * 11. 63 bps ≈ 34, 880 bps ≈ 35 kbps 16

B it Rate (continue. . . ) Shannon’s Result u u Shannon’s result is not just a theoretical result; rather it has its very real implication During the 1980 s, 2400 & 9600 bps modems became common Early 1990 s, modems with a rate of 28. 8 and 33. 6 kbps became common (this matched the maximum bit rate that Shannon’s result indicated) Not much longer, modems that supported 56. 6 kbps rates were a reality. Did this violate Shannon’s results? 17

D igital-to-Analog-Conversion u Computers are digital, however phone lines connecting them to remote machines/servers are analog Figure 3. 11 – Computer Data Transmitted Over Telephone Lines 18

D igital-to-Analog-Conversion u u New phone lines use optical fiber, which carry digital signal Codec (Coder/Decoder) is needed in such cases Figure 3. 12 – Voice Information Transmitted Digitally 19

D igital-to-Analog-Conversion Frequency Modulation (FM) u u u Simple method of digital to analog conversion, Also known as Frequency Shift Keying (FSK) Assigns digital 0 to one signal and 1 to another based on some rule In general, if n bits are sent per baud, then we can have 2 n signal combination The signal is transmitted for a fixed period of time Figure 3. 13 – FSK (Two Frequencies), One Bit per Baud – Analog signal for 01001 20

D igital-to-Analog-Conversion Amplitude Modulation (AM) u u u Also known as Amplitude Shift Keying (ASK) Each bit group is assigned to an analog signal of given magnitude The signal is transmitted for a fixed period of time as with FM Figure 3. 14 – ASK (Four Amplitudes), Two Bits per Baud – Analog signal for 00110110 21

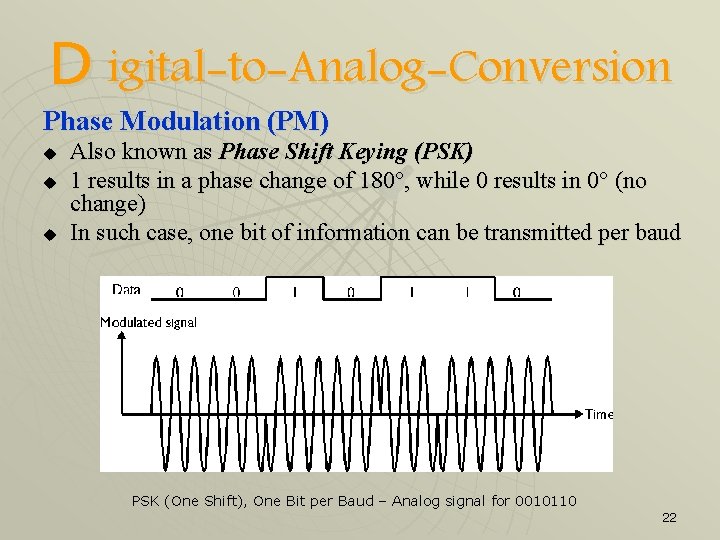
D igital-to-Analog-Conversion Phase Modulation (PM) u u u Also known as Phase Shift Keying (PSK) 1 results in a phase change of 180°, while 0 results in 0° (no change) In such case, one bit of information can be transmitted per baud PSK (One Shift), One Bit per Baud – Analog signal for 0010110 22

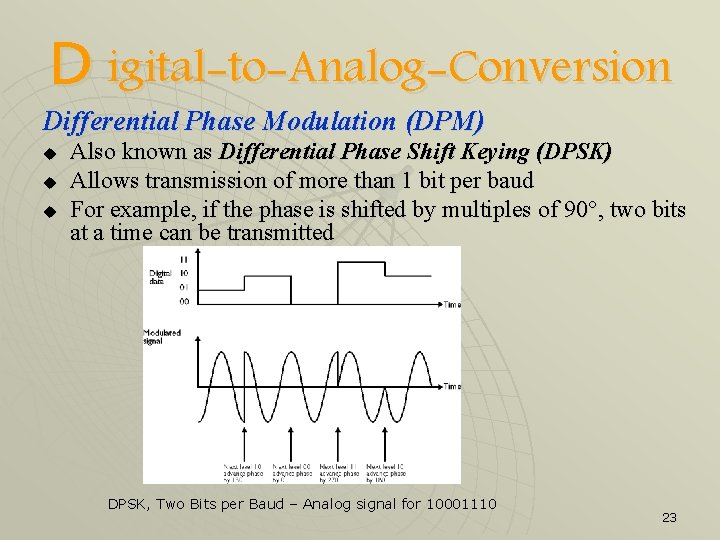
D igital-to-Analog-Conversion Differential Phase Modulation (DPM) u u u Also known as Differential Phase Shift Keying (DPSK) Allows transmission of more than 1 bit per baud For example, if the phase is shifted by multiples of 90°, two bits at a time can be transmitted DPSK, Two Bits per Baud – Analog signal for 10001110 23

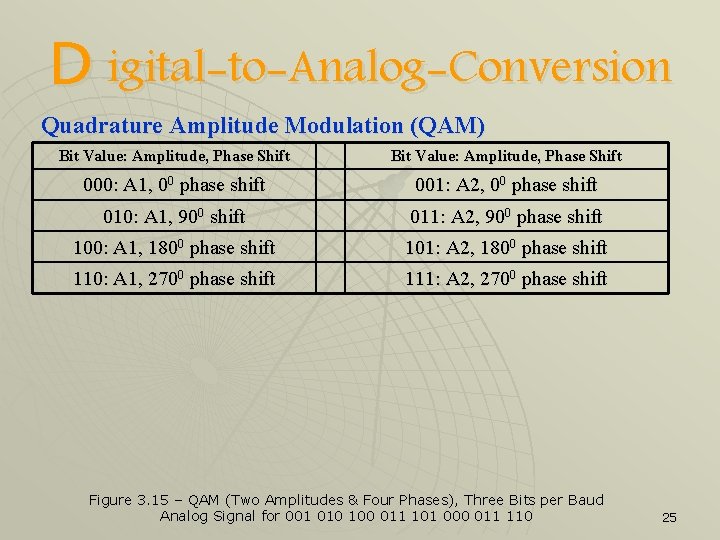
D igital-to-Analog-Conversion Quadrature Amplitude Modulation (QAM) u u A greater signal variety means a greater bit rate per baud rate The problem is that the higher the number of signal, the smaller the difference among them One common approach to avoid that is to use a combination of frequencies, amplitudes or phase shifts to allow a large group of bits while marinating a larger differences among them QAM is a common technique in which a group of bits is assigned a signal defined by its amplitude and phase shift 24

D igital-to-Analog-Conversion Quadrature Amplitude Modulation (QAM) Bit Value: Amplitude, Phase Shift 000: A 1, 00 phase shift 001: A 2, 00 phase shift 010: A 1, 900 shift 011: A 2, 900 phase shift 100: A 1, 1800 phase shift 101: A 2, 1800 phase shift 110: A 1, 2700 phase shift 111: A 2, 2700 phase shift Figure 3. 15 – QAM (Two Amplitudes & Four Phases), Three Bits per Baud Analog Signal for 001 010 100 011 101 000 011 110 25

A nalog-to-Digital-Conversion u u Some analog-to-digital conversion is nothing but the opposite to what has been discussed, however, Other conversions are more complex; for example those that are required to convert analog data for voice or music 26

A nalog-to-Digital-Conversion Pulse Amplitude Modulation (PAM) u An analog signal is sampled at a regular interval, then a pulse with amplitude equal to the sampled signal is generated Figure 3. 17 – Pulse Amplitude Modulation 27

A nalog-to-Digital-Conversion Pulse Code Modulation (PCM) u PAM-generated signals look digital, but the signal has analog characteristics u PCM allows the signal to truly be digital by assigning amplitude from a predefined set of digital codes u By sampling s times per second, we obtain a bit rate of n * s bps Figure 3. 18 – Pulse Code Modulation, n=3, 2 n codes 28

A nalog-to-Digital-Conversion Pulse Code Modulation (PCM) u At the receiving end, the accuracy of the construction depends on: • Sampling frequency: a slower sampling frequency may result in some oscillations to be missed entirely u u u higher sampling rate will produce a higher accuracy; but up to a point Based on Nyquist theorem, if the original signal has f maximum frequency, then sampling at 2 f is enough That is, sampling at a higher rate than 2 f will not produce any better accuracy than 2 f • Number of amplitude (binary codes) from which to choose u u The higher the difference between the sampled signal and the pulse/code, the higher the chances that the reconstructed signal become distorted This is called, quantization noise It should be noted however that higher sampling and higher number of pulse amplitude comes with a price Figure 3. 19 – Sampling at Too Low Frequency 29

A nalog-to-Digital-Conversion Pulse Code Modulation (PCM) u PAM has several common applications; which include • Digitizing of voice signal over long-distance telephone lines u 8000 samples, with 8 -bit sample bit rate of 64 kbps • Compact discs (CDs) Varies from one device to another u As an example: 44. 1 k. Hz sampling frequency, with a D-A conversion of 16 -bit linear u 16 -bit would allow 64, 000 amplitude (linear indicates that the differences between these amplitudes are the same) u 30

M odems Two important issues are there with modems u u u • Software (deliver signals to and from modem) • Compatibility (demodulate what other modems modulated) Several standards were defined for modems CCITT (ITU) defined V. xx series of modem standards V. 21 uses FSK with 1 frequency for 1 bit, and the resulting bit rate is equal to the baud rate. (supports up to 300 bps. ) V. 22 uses PSK with 2 bits for each phase shift; resulting bit rate is twice the baud rate. 600 bauds/sec = 1200 bps Sending and receiving modems use different frequency; that enable full-duplex communication 31

M odems (continue. . . ) Signal Constellation u u u Many modems work by changing more than one analog signal’s components, typically phase shift & amplitude (QAM) QAM can visually be described a signal constellation graph Distance represents amplitude, while angel represents phase shift Figure 3. 20 – Quantifying a Point on a signal Constellation 32

M odems (continue. . . ) Signal Constellation u u A shift with x° corresponds to x/360° of a period V. 22 uses fixed amplitude with 4 (22) points and 600 bauds 600 * 2 = 1200 bps V. 22 bis uses 16 (24) points and 600 bauds 600 * 4 = 2400 bps V. 32 uses 5 bits per baud but one of them is for Trellis Coding error detection 16 (24) points are counting and 2400 bauds 2400 * 4 = 9600 bps Figure 3. 21 – Quantifying a Point on a signal Constellation 33

M odems (continue. . . ) Signal Constellation u Distortion is possible, which may change the amplitude or the phase shift Figure 3. 22 – Distortion of Signal Constellation Points 34

M odems (continue. . . ) Signal Constellation u Depending on the distortion level, the modem may or may not be able to interpret the distorted signal correctly Figure 3. 23 – Interpreting Constellation Points for a distorted signal 35

M odems (continue. . . ) Modem Standards u u Few modem standards exist! They differ in baud rate, bit per baud, modulation techniques, error detection, compressions, . . etc. Autobaud modems exist and convenient since they are capable of automatically choose the appropriate standard; they also allow users to communicate using any of several standards 56 kbps modems were achievable when connecting directly with ISP Figure 3. 24 – Connections using a Modem 36

M odems (continue. . . ) Cable Modems u u Driven by many facts including the inability of modem over phone lines to go beyond 56 kbps They connect with the analog component of a cable TV (CATV) instead of the analog component of the telephone system Figure 3. 25 – Cable Modem Placement 37

M odems (continue. . . ) Cable Modems u u Utilizes the much higher frequency of CATV, so few Mbps speed is achieved However bit rate may differ depending on the number of users (neighbors usually!) that are using the cable line 38

M odems (continue. . . ) Cable Modems u u Usually has a frequency of about 750 MHz, divided into many 6 -MHz for different channels Information from the Internet can be downloaded onto a 6 MHz band somewhere between 42 and 750 MHz Figure 3. 26 – Cable Modem & Carrier Signals 39

M odems (continue. . . ) Cable Modems u A number of techniques can be used for modulating & demodulating, but two are more popular: • Quaternary Phase Shift Keying (QPSK) • QAM 64, a variation of QAM u u QAM 64 is typical for high bandwidth requirement – data download rate can be 36 Mbps, which many PCs today are not capable of handling A more realistic figure is between 1 and 11 Mbps 40

M odems (continue. . . ) Cable Modems u u Can also be used to transmit information on the opposite direction (Uploading) Frequency used for uploading is usually between 5 & 40 MHz • Uploading has lower bit rate, which might be okay. Why? 41

D SL u u DSL - Digital Subscriber Line Fast and does not require cable wiring or dialing up to ISP Uses telephone lines!!!! Local loop (last mile) is capable of transmitting signals of up to 1 MHz frequency, that Local exchange can receive Figure 3. 27 – Local Loop - POTS (Plain Old Telephone Service) Configuration 42

D SL Various forms of DSL exist (continue. . . ) Asymmetric DSL Figure 3. 28 – ADSL Connection 43

ADSL Lite u D SL (continue. . . ) Designed for residential customers Figure 3. 30 – ADSL Lite 44

D SL (continue. . . ) VDSL – Very High Data Rate DSL u u u The local loop causes many DSL problems Signal degrades over long distance, do DSL is not available if the house is more than 3. 5 miles from the local office New improved local loop using fiber/copper hybrid is used, which improves quality, reduces the copper length and makes VDSL possible Figure 3. 31 – Local Loop: Fiber/Copper Hybrid 45