Analiza ponaanja trokova Uvod Analiza ponaanja trokova podrazumijeva

Analiza ponašanja troškova

Uvod • Analiza ponašanja troškova podrazumijeva poznavanje veličine varijabilnih i poznavanje veličine fiksnih troškova. • U svakodnevnom životu troškovi nastaju bez opisa tog njihovog obilježja što znači da svaki trošak treba proučiti da bi se utvrdilo je li taj trošak fiksan ili varijabilan. • Pojedini se troškovi ne mijenjaju s razinom prodaje, ali se mijenjaju sa nekom drugom aktivnosti poduzeća. • Neki od troškova pojavljuju se kao mješoviti troškovi (kombinacija fiksnih i varijabilnih troškova).

Svrha analize troškova • Za obavljanje svoje funkcije menadžeri moraju razumjeti ponašanje troškova, prije svega za potrebe planiranja. • Mogućnosti procjenjivanja veličine varijabilnih troškova za utvrđivanje graničnog prinosa kao izuzetno važnog čimbenika u donošenju odluka. • Menadžeri moraju razumjeti ponašanje troškova za obavljanje funkcije nadzora. • Analiza troškova je također vrlo značajna s obzirom na ulogu koju ima u upravljanju troškovima.

Utvrđivanje ponašanja troškova • • Računovodstvena analiza Inžinjerski pristup Metoda gornje i donje točke (high - low method) Metoda dijagrama rasipanja (scatter - diagram method) • Regresijska metoda • Korelacija i asocija • Lažna korelacija

Računovodstvena analiza • Jednostavna i često vrlo učinkovita metoda utvrđivanja ponašanja troškova. • Klasifikacija troškova prema prirodnoj vrsti troškova. • Provode je računovođe. • Primjerice, troškovi kao što su najam, amortizacija, plaće i oglašavanje općenito se klasificiraju kao fiksni troškovi. • Ograničenje: ovakvu je analizu moguće provesti za relativno mali broj troškova, dok istovremeno može dati potpuno pogrešne rezultate. • Primjerice, troškovi amortizacije obično su fiksni troškova, ali u određenim situacijama mogu biti djelomično varijabilni troškovi.

Inžinjerski pristup • Vrlo uspješno se primjenjuje pri utvrđivanju jediničnih varijabilnih troškova u proizvodnim poduzećima. • Primjerice, ovim se načinom utvrđuju troškovi materijala i rada potrebni za proizvodnju proizvoda, nakon čega se procjenjuju jedinični troškovi koji bi se trebali mijenjati s količinom proizvodnje. • Metoda industrijskog inžinjeringa obuhvaća tehnike procjene utemeljene na tehnološkim standardima i odnosima. • Inžinjerski pristup nije naročito pogodan u procjeni neproizvodnih troškova.

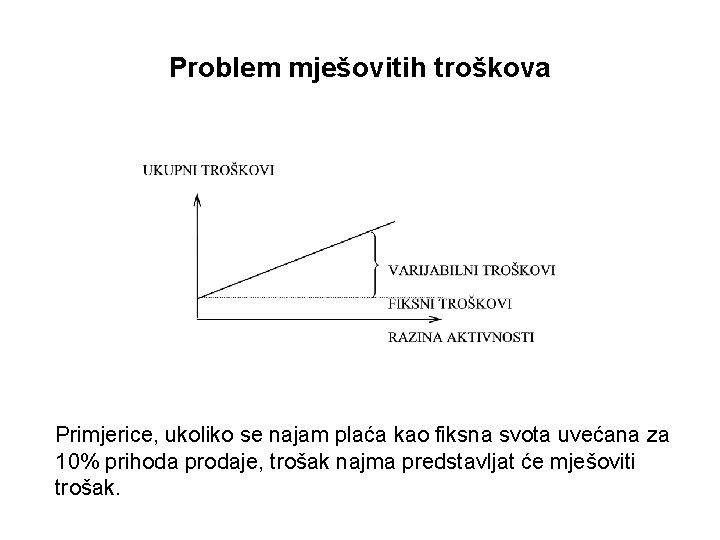
Problem mješovitih troškova • Ponekad analize ukazuju da je određeni trošak upravo fiksan ili upravo varijabilan. No, analize najčešće ukazuju da je određeni trošak mješovit (semivariable cost). • Mješoviti troškovi sadrže i fiksnu i varijabilnu komponentu. • Niti jedna od prethodno spomenutih metoda utvrđivanja ponašanja troškova ne može se uspješno primijeniti ukoliko je riječ o mješovitim troškovima.

Problem mješovitih troškova Primjerice, ukoliko se najam plaća kao fiksna svota uvećana za 10% prihoda prodaje, trošak najma predstavljat će mješoviti trošak.

Metoda gornje i donje točke • Iako relativno neznanstvena, no istovremeno vrlo primjenjivana metoda procjene komponenti mješovitih troškova jest metoda gornje i donje točke (metoda dviju točaka, metoda najvišeg i najnižeg stupnja zaposlenosti, metoda visoko - nisko). • Ova metoda koristi dvije razine aktivnosti i svote pripadajućih troškova tih razina aktivnosti. • Gornja i donja točka odnose se na najvišu i najnižu razinu neke aktivnosti, odnosno na najvišu i najnižu razinu troškova odabranih razina aktivnosti određenog intervala.

Metoda gornje i donje točke Za pronalaženje varijabilne komponente troškova, razlika u troškovima između dviju postavljenih točaka dijeli se s razlikom u razinama aktivnosti koje su izazvale te troškove. Formula za izračunavanje varijabilnih troškova po jedinici jest:

Metoda gornje i donje točke Funkcija predviđanja troškova plaća bila bi, polazeći od linearne funkcije oblika y = ax + b, sljedeća: UT = (jedinični VT × x) + FT

Metoda gornje i donje točke • U prethodnom je slučaju evidentno da razina prodaje (neovisna varijabla) utječe na veličinu troškova (ovisna varijabla) te se stoga razina prodaje koristi kao mjera razine aktivnosti. • U nekom drugom slučaju bi razina proizvodnje ili neka druga mjera aktivnosti mogla biti uzročnikom promjene troškova. • Općenito, u ovakvoj analizi troškova i jest najveći problem pronaći aktivnost koja izaziva nastanak troškova (cost driver). • Da bi se metodom gornje i donje točke moglo predvidjeti buduće kretanje troškova, analizu troškova treba postaviti unutar relevantnog uzorka. • Relevantni uzorak jest onaj uzorak za kojeg se može pretpostaviti proporcionalno kretanje varijabilnih troškova s promjenom razine aktivnosti, pri čemu fiksni troškovi ostaju nepromijenjeni.

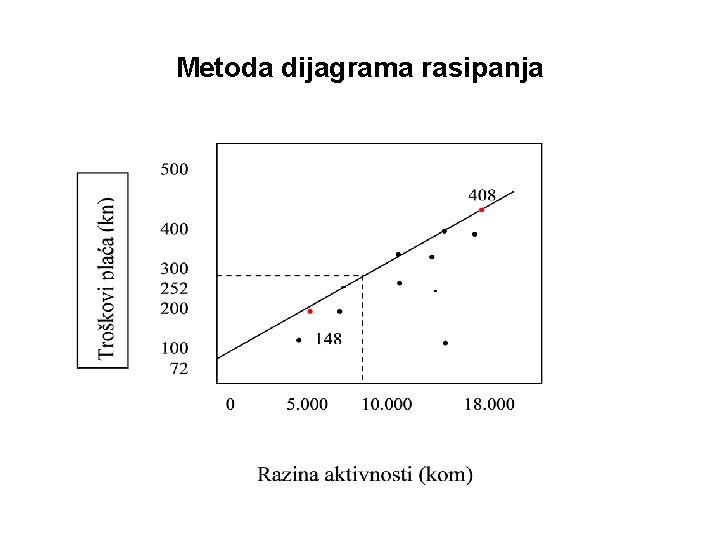
Metoda dijagrama rasipanja • Slično metodi gornje i donje točke, i metoda dijagrama rasipanja (metoda linije trenda, grafička metoda) koristi podatke o troškovima i razinama aktivnosti prošlih razdoblja. • Prvi korak u formiranju dijagrama rasipanja jest nacrtati točke ukupnih troškova za različite razine aktivnosti relevantnog uzorka. • Drugi korak jest ucrtati pravac koji će se maksimalno približiti svim ucrtanim točkama. • Položaj pravca i njegov nagib (parametar a) ovise o procjeni analitičara. Koliko je pravac dobro postavljen, procjenjuje se “od oka”.

Metoda dijagrama rasipanja

Metoda regresijske analize Sofisticiranija metoda procjene fiksne i varijabilne komponente u mješovitim troškovima jest metoda regresijske analize (metoda najmanjih kvadrata). Slično prethodnim metodama, i ova statistička metoda rabi podatke o troškovima i razinama aktivnosti prošlih razdoblja te rezultira, u svom najjednostavnijem obliku, jednadžbom u sljedećem obliku: y = ax + b Ukupni troškovi = FT + (jedinični VT po razini aktivnosti × razina aktivnosti)

Metoda regresijske analize Za razliku od metode gornje i donje točke, regresijska analiza koristi sve raspoložive podatke, a ne samo one za dvije točke. Za razliku od metode dijagrama rasipanja, regresijska analiza temelji se na statističkom konceptu matematičkog izračuna funkcije koja najbolje reprezentira niz pri čemu svi analitičari, promatrajući iste podatke, dolaze do istog pravac, a ne na subjektivnoj procjeni analitičara pri ucrtavanju pravca kretanja troškova.

Metoda regresijske analize - primjer

Metoda regresijske analize - primjer

Metoda regresijske analize - primjer

Korelacija i asocija • Samo postavljanje jednadžbi i funkcija za predviđanje ponašanja troškova nije dovoljno. • Da bi jednadžba bila uporabljiva, odnos mjerenih troškova i razine aktivnosti mora biti u međuzavisnosti korelacija ili asocija

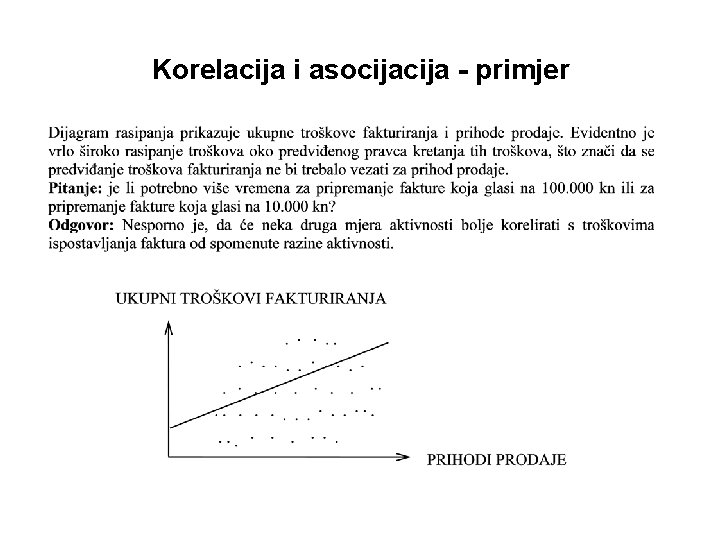
Korelacija i asocija - primjer

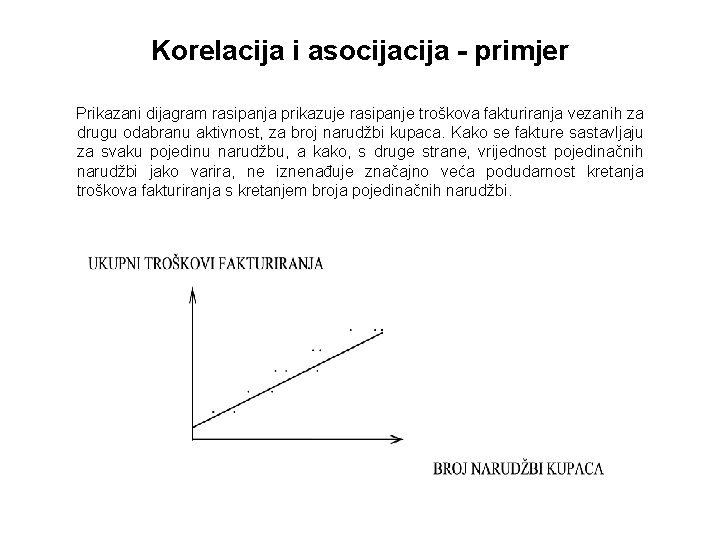
Korelacija i asocija - primjer Prikazani dijagram rasipanja prikazuje rasipanje troškova fakturiranja vezanih za drugu odabranu aktivnost, za broj narudžbi kupaca. Kako se fakture sastavljaju za svaku pojedinu narudžbu, a kako, s druge strane, vrijednost pojedinačnih narudžbi jako varira, ne iznenađuje značajno veća podudarnost kretanja troškova fakturiranja s kretanjem broja pojedinačnih narudžbi.

Primjer za vježbu br. 1 Poduzeće koje proizvodi fasadnu boju imalo je sljedeće troškove materijala i proizvedenu količinu boje u posljednja tri mjeseca: Pitanja: a) Koristeći metodu gornje i donje točke, izračunajte jedinične varijabilne troškove! b) Koristeći navedene podatke, izračunajte fiksne troškove za jednu od razina aktivnosti! c) Temeljem dobivenih podataka, postavite funkciju predviđanja ukupnih troškova materijala! d) Temeljem postavljene funkcije predviđanja troškova, procijenite troškove materijala pri razini aktivnosti od 60 l boje.

Rješenje primjera za vježbu br. 1 Pitanja: a) Koristeći metodu gornje i donje točke, izračunajte jedinične varijabilne troškove! b) Koristeći navedene podatke, izračunajte fiksne troškove za jednu od razina aktivnosti!

Rješenje primjera za vježbu br. 1 Pitanja: c) Temeljem dobivenih podataka, postavite funkciju predviđanja ukupnih troškova materijala! d) Temeljem postavljene funkcije predviđanja troškova, procijenite troškove materijala pri razini aktivnosti od 60 l boje.

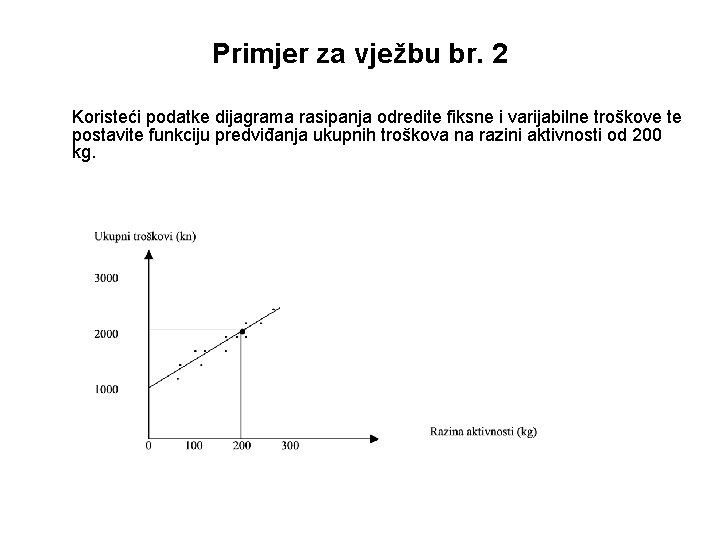
Primjer za vježbu br. 2 Koristeći podatke dijagrama rasipanja odredite fiksne i varijabilne troškove te postavite funkciju predviđanja ukupnih troškova na razini aktivnosti od 200 kg.

Rješenje primjera za vježbu br. 2