ANALISIS VECTORIAL SISTEMA DE COORDENADAS EN EL PLANO

ANALISIS VECTORIAL SISTEMA DE COORDENADAS EN EL PLANO SUMA VECTORIAL RESTA VECTORIAL PRODUCTO ESCALAR PRODUCTO VECTORIAL POSICION VECTORIAL VECTORES EN EL ESPACIO FISICA DR. VICTOR HUGO CAIZA R.

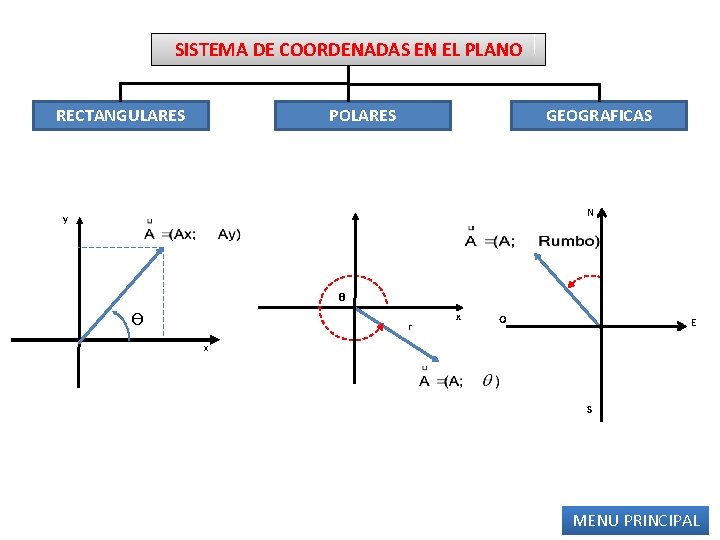
SISTEMA DE COORDENADAS EN EL PLANO RECTANGULARES POLARES GEOGRAFICAS N y θ ϴ r X O E x S MENU PRINCIPAL

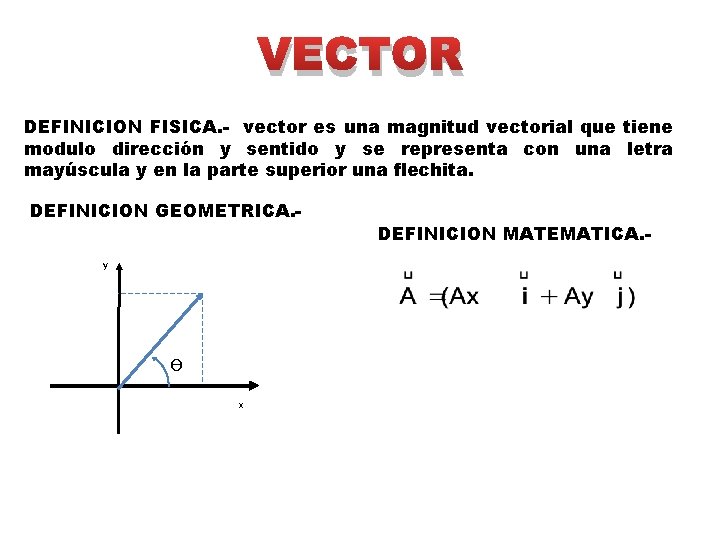
VECTOR DEFINICION FISICA. - vector es una magnitud vectorial que tiene modulo dirección y sentido y se representa con una letra mayúscula y en la parte superior una flechita. DEFINICION GEOMETRICA. y ϴ x DEFINICION MATEMATICA. -

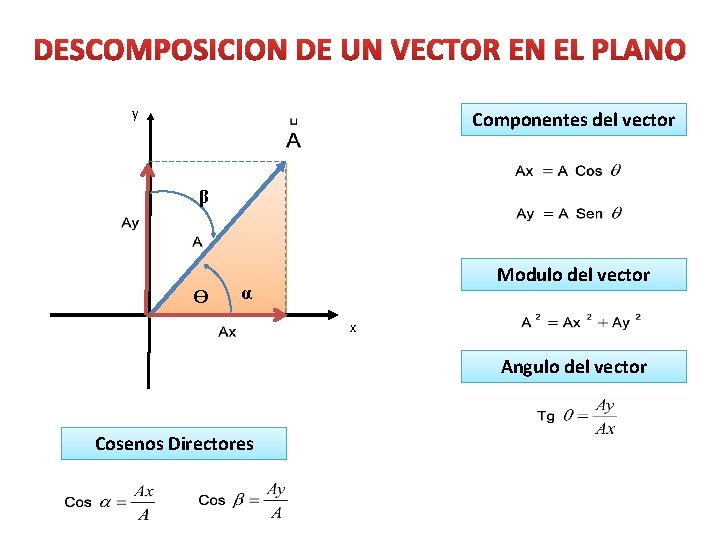
DESCOMPOSICION DE UN VECTOR EN EL PLANO y Componentes del vector β ϴ Modulo del vector α x Angulo del vector Cosenos Directores

FORMAS DE EXPRESAR UN VECTOR EN FUNCIÓN DE SU MÓDULO Y ÁNGULO (POLARES) EN FUNCIÓN DE SUS COORDENADAS RECTANGULARES EN FUNCIÓN DE SUS VECTORES BASE EN FUNCIÓN DE SUS COORDENADAS GEOGRAFICAS EN FUNCIÓN DE SU MÓDULO Y UNITARIO

EJERCICIO Nº 1 1)Expresar el vector. En: a) Coordenadas polares. b) Función de su vector base. c) Coordenadas geográficas. d) Función de su módulo y unitario. DATOS Ax=-5 cm Ay= 8 cm 57, 99º

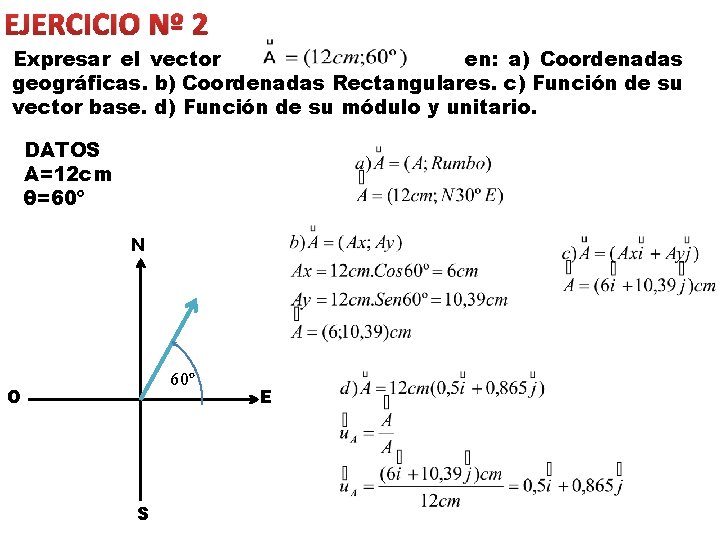
EJERCICIO Nº 2 Expresar el vector en: a) Coordenadas geográficas. b) Coordenadas Rectangulares. c) Función de su vector base. d) Función de su módulo y unitario. DATOS A=12 cm θ=60º N 60º O S E

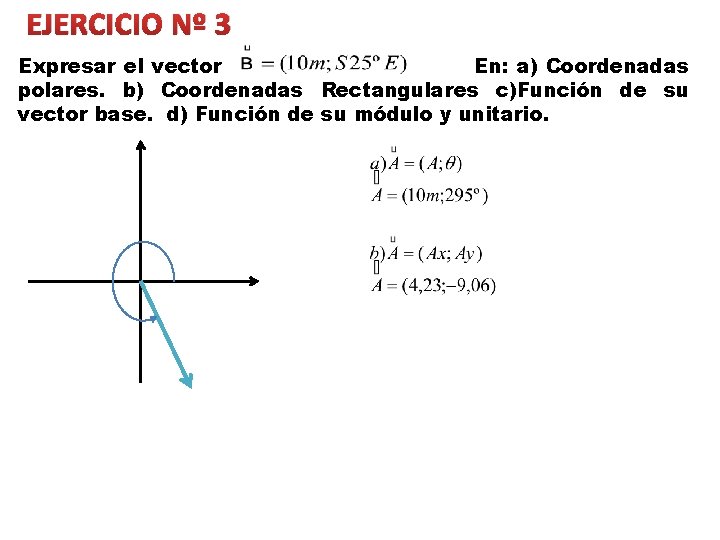
EJERCICIO Nº 3 Expresar el vector En: a) Coordenadas polares. b) Coordenadas Rectangulares c)Función de su vector base. d) Función de su módulo y unitario.

EJERCICIO Nº 4 Expresar el vector En: a) Coordenadas polares. b) Función de su vector base. c) Coordenadas geográficas. d) Función de su módulo y unitario. N O S

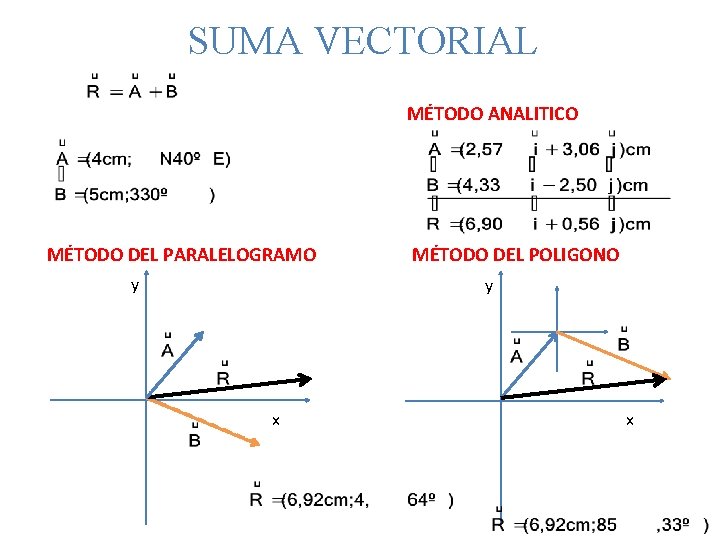
SUMA VECTORIAL MÉTODO ANALITICO MÉTODO DEL PARALELOGRAMO y MÉTODO DEL POLIGONO y x x

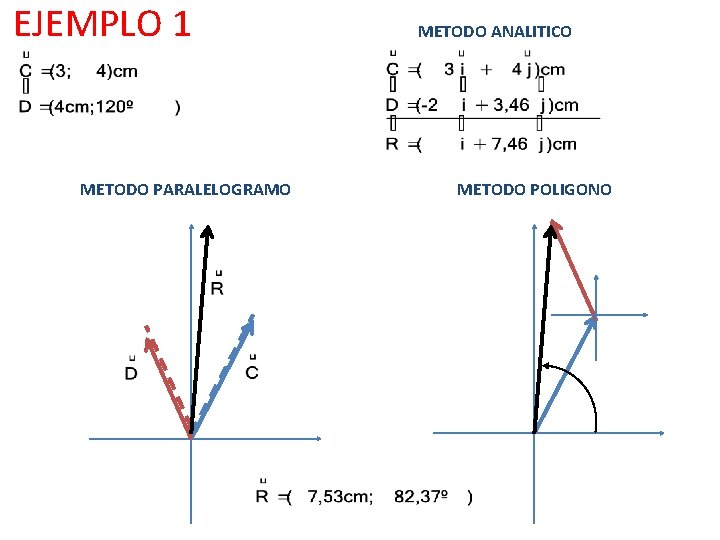
EJEMPLO 1 METODO PARALELOGRAMO METODO ANALITICO METODO POLIGONO

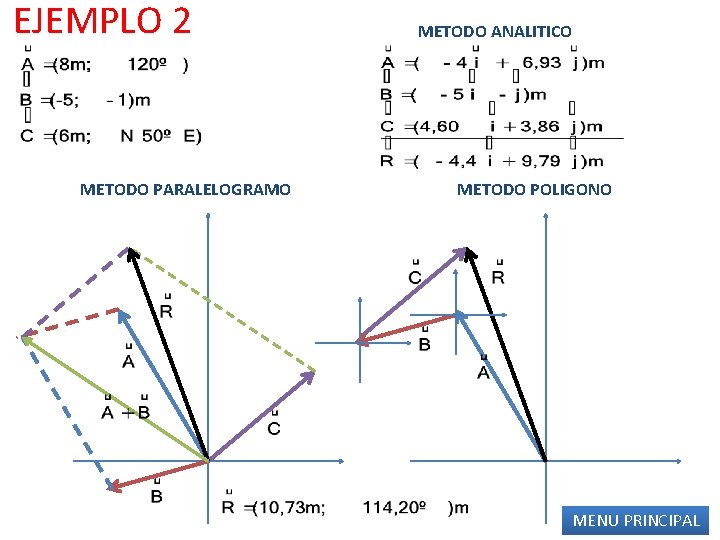
EJEMPLO 2 METODO PARALELOGRAMO METODO ANALITICO METODO POLIGONO MENU PRINCIPAL

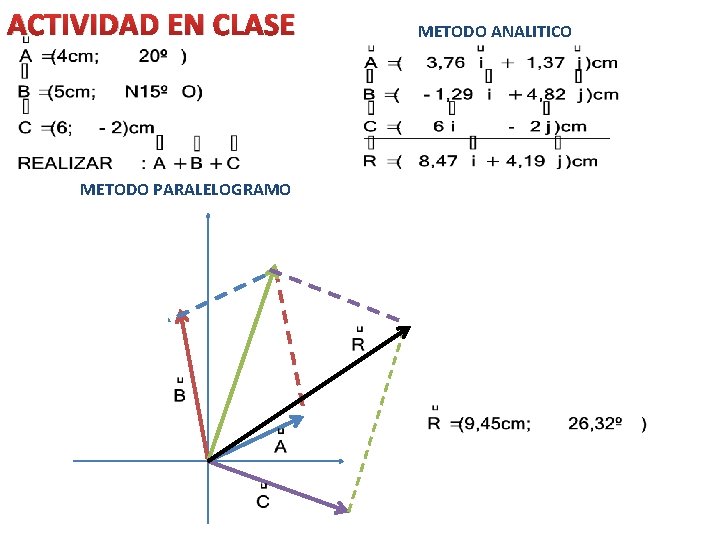
ACTIVIDAD EN CLASE METODO PARALELOGRAMO METODO ANALITICO

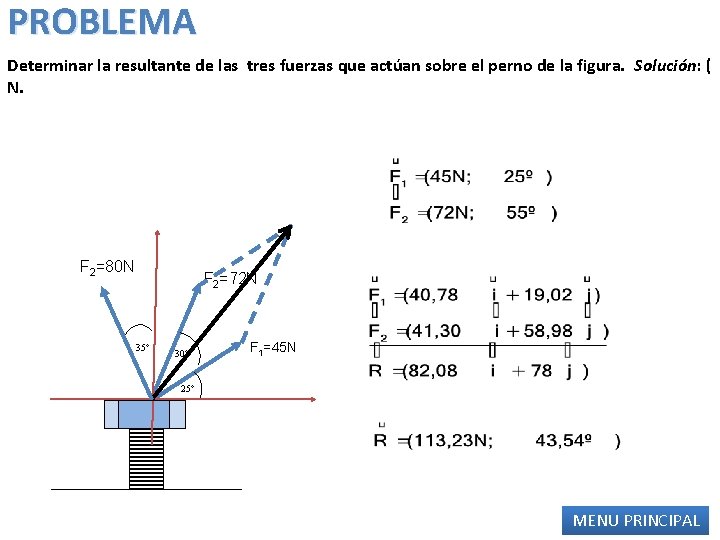
PROBLEMA Determinar la resultante de las tres fuerzas que actúan sobre el perno de la figura. Solución: ( N. F 2=80 N F 2=72 N 35º 30º F 1=45 N 25º MENU PRINCIPAL

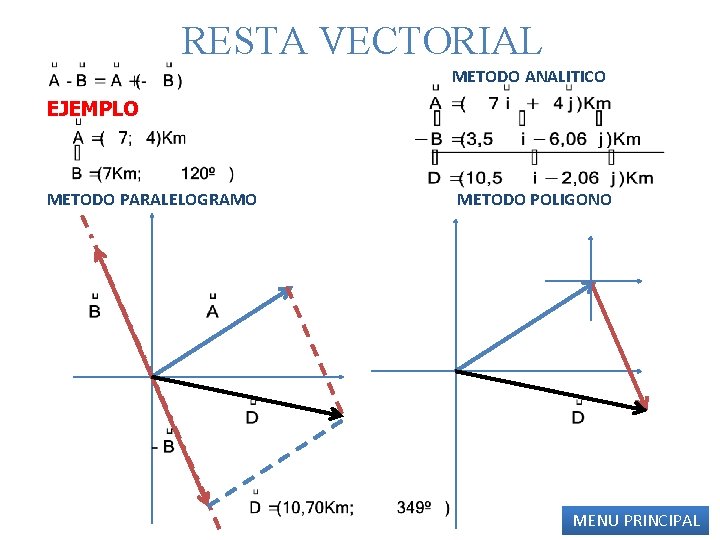
RESTA VECTORIAL METODO ANALITICO EJEMPLO METODO PARALELOGRAMO METODO POLIGONO MENU PRINCIPAL

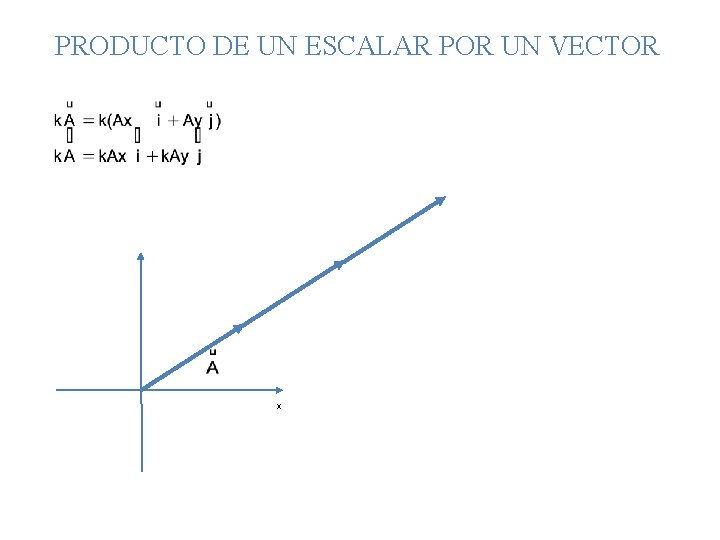
PRODUCTO DE UN ESCALAR POR UN VECTOR x

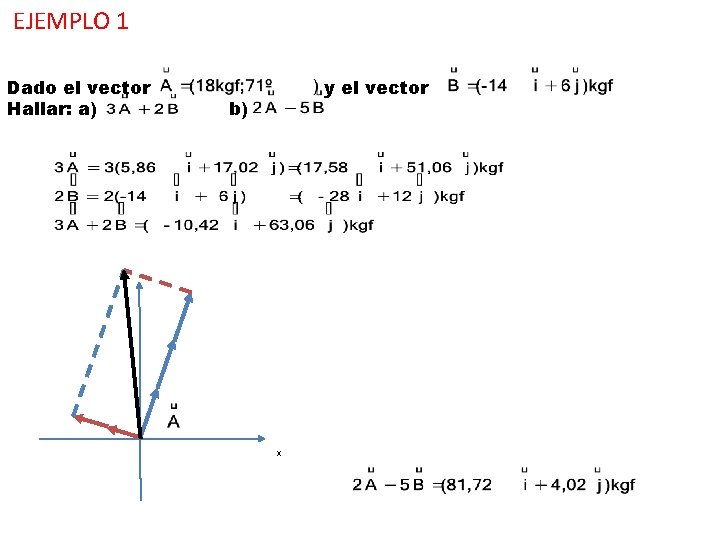
EJEMPLO 1 Dado el vector Hallar: a) y el vector b) x

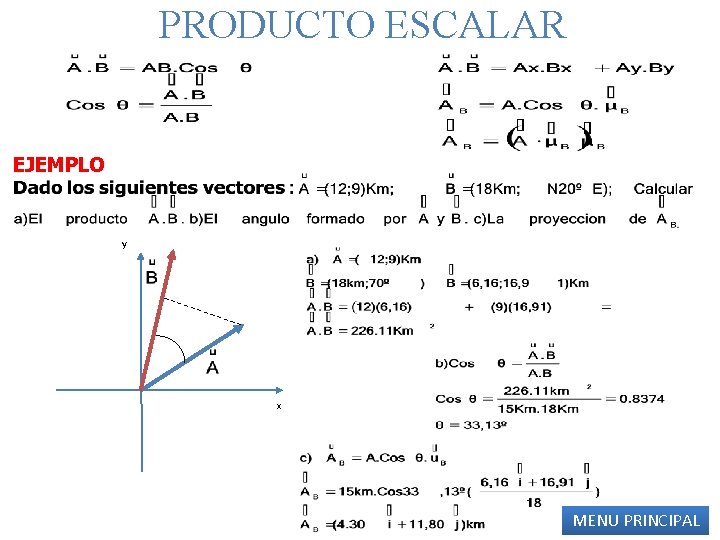
PRODUCTO ESCALAR EJEMPLO y x MENU PRINCIPAL

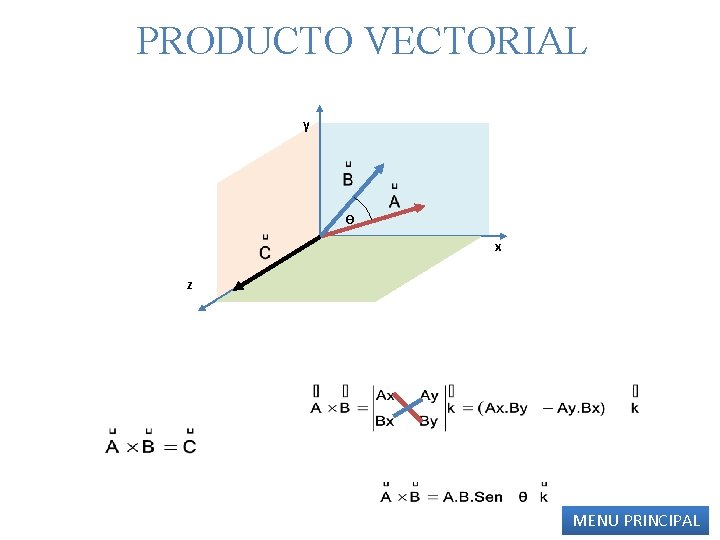
PRODUCTO VECTORIAL y ϴ x z MENU PRINCIPAL

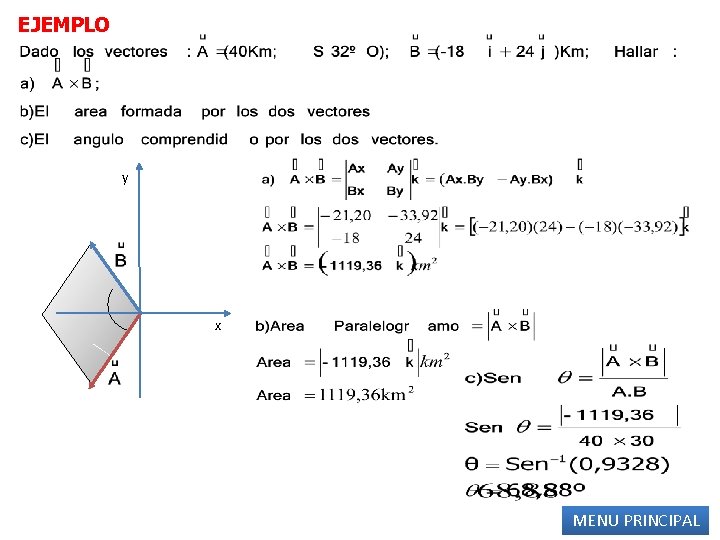
EJEMPLO y x MENU PRINCIPAL

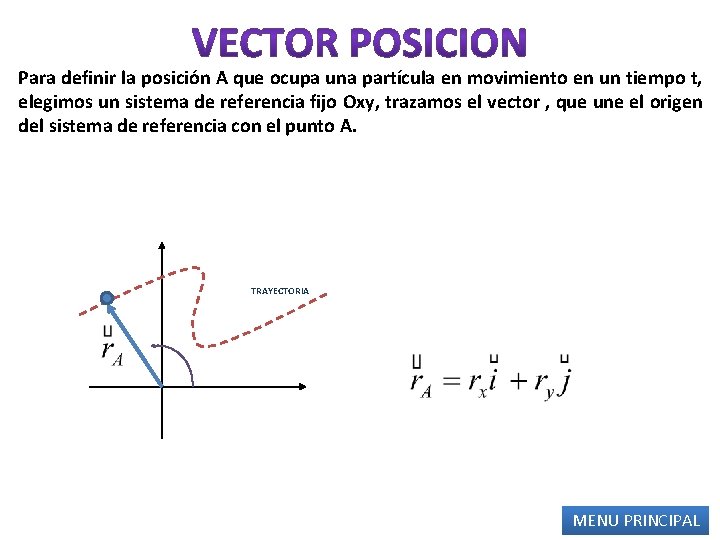
Para definir la posición A que ocupa una partícula en movimiento en un tiempo t, elegimos un sistema de referencia fijo Oxy, trazamos el vector , que une el origen del sistema de referencia con el punto A. TRAYECTORIA MENU PRINCIPAL

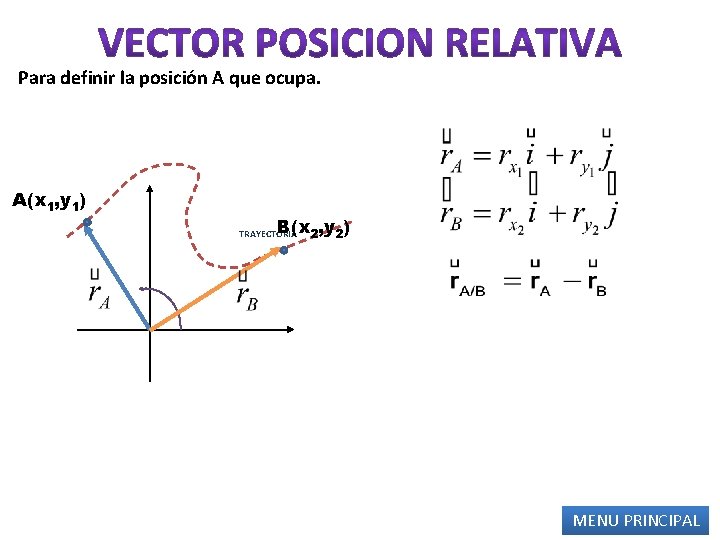
Para definir la posición A que ocupa. A(x 1, y 1) B(x 2, y 2) TRAYECTORIA MENU PRINCIPAL

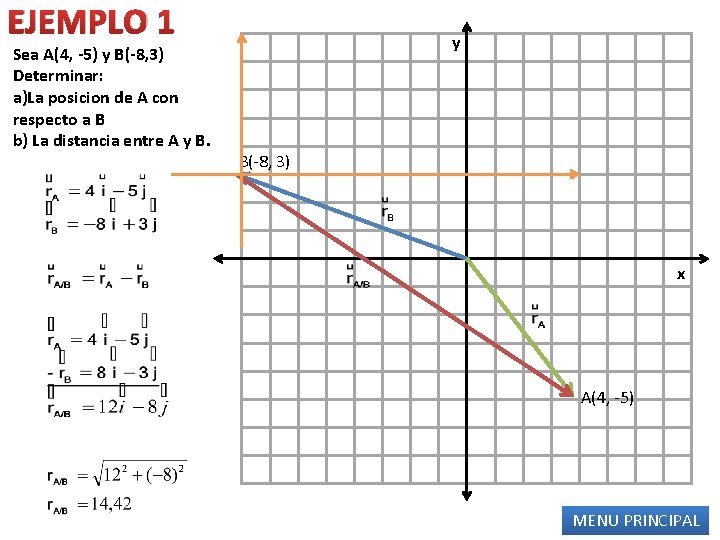
EJEMPLO 1 Sea A(4, -5) y B(-8, 3) Determinar: a)La posicion de A con respecto a B b) La distancia entre A y B(-8, 3) x A(4, -5) MENU PRINCIPAL

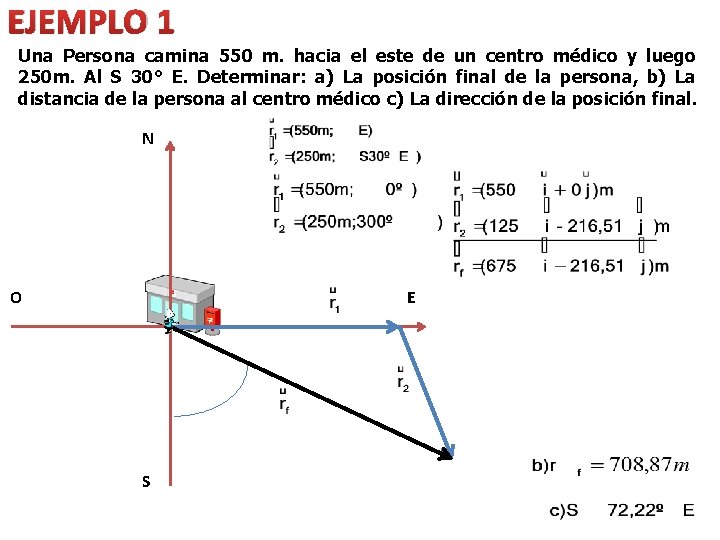
EJEMPLO 1 Una Persona camina 550 m. hacia el este de un centro médico y luego 250 m. Al S 30° E. Determinar: a) La posición final de la persona, b) La distancia de la persona al centro médico c) La dirección de la posición final. N O E S

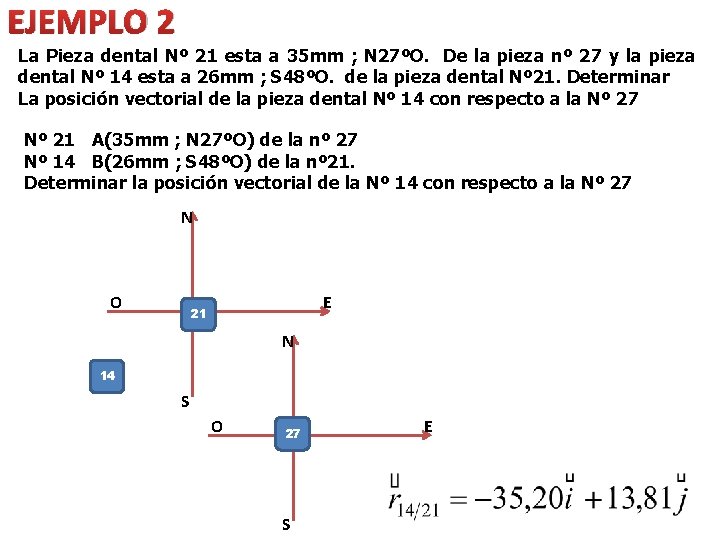
EJEMPLO 2 La Pieza dental Nº 21 esta a 35 mm ; N 27ºO. De la pieza nº 27 y la pieza dental Nº 14 esta a 26 mm ; S 48ºO. de la pieza dental Nº 21. Determinar La posición vectorial de la pieza dental Nº 14 con respecto a la Nº 27 Nº 21 A(35 mm ; N 27ºO) de la nº 27 Nº 14 B(26 mm ; S 48ºO) de la nº 21. Determinar la posición vectorial de la Nº 14 con respecto a la Nº 27 N O E 21 N 14 S O 27 S E

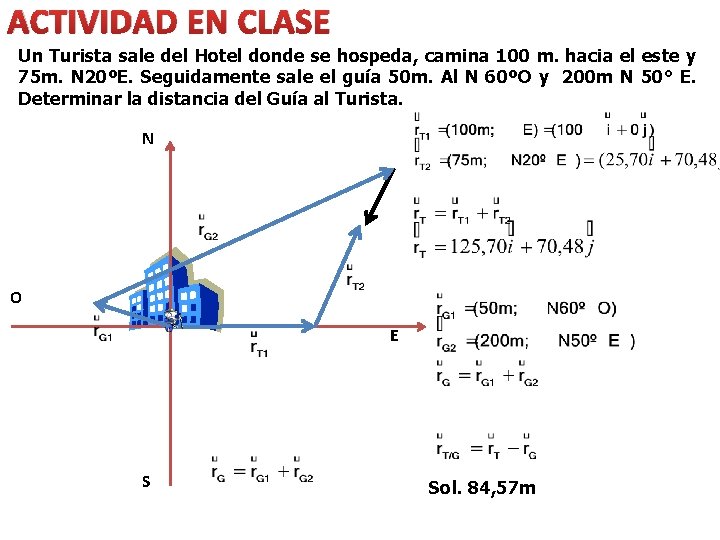
ACTIVIDAD EN CLASE Un Turista sale del Hotel donde se hospeda, camina 100 m. hacia el este y 75 m. N 20ºE. Seguidamente sale el guía 50 m. Al N 60ºO y 200 m N 50° E. Determinar la distancia del Guía al Turista. N O E S Sol. 84, 57 m

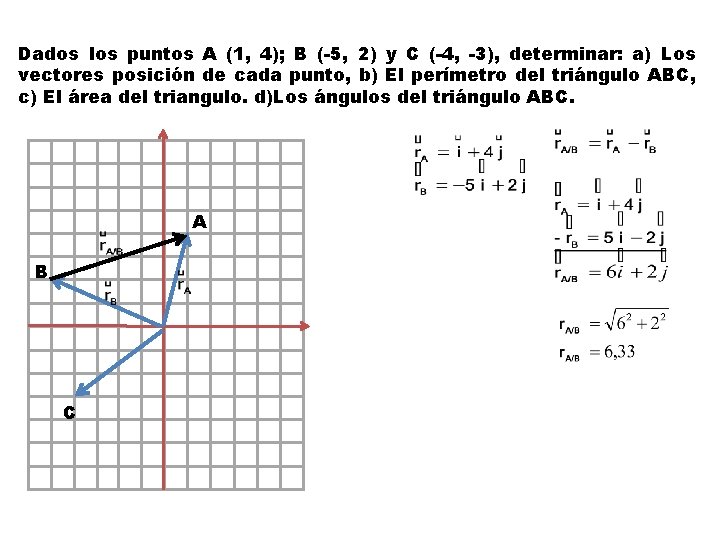
Dados los puntos A (1, 4); B (-5, 2) y C (-4, -3), determinar: a) Los vectores posición de cada punto, b) El perímetro del triángulo ABC, c) El área del triangulo. d)Los ángulos del triángulo ABC. A B C

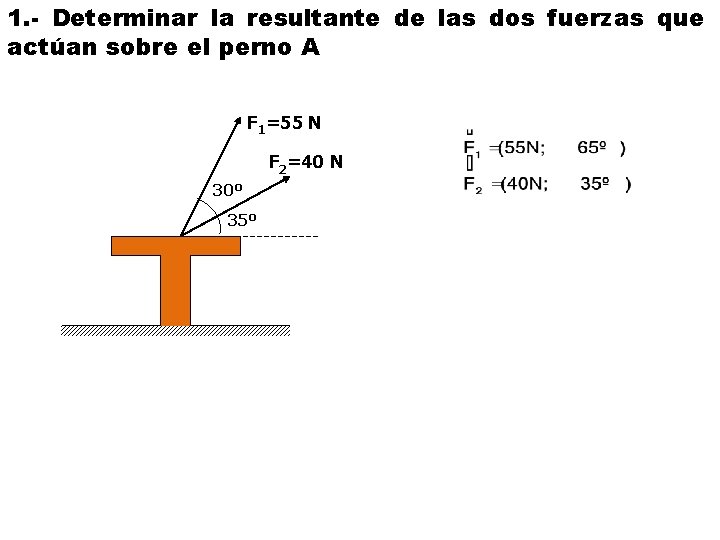
1. - Determinar la resultante de las dos fuerzas que actúan sobre el perno A F 1=55 N F 2=40 N 30º 35º

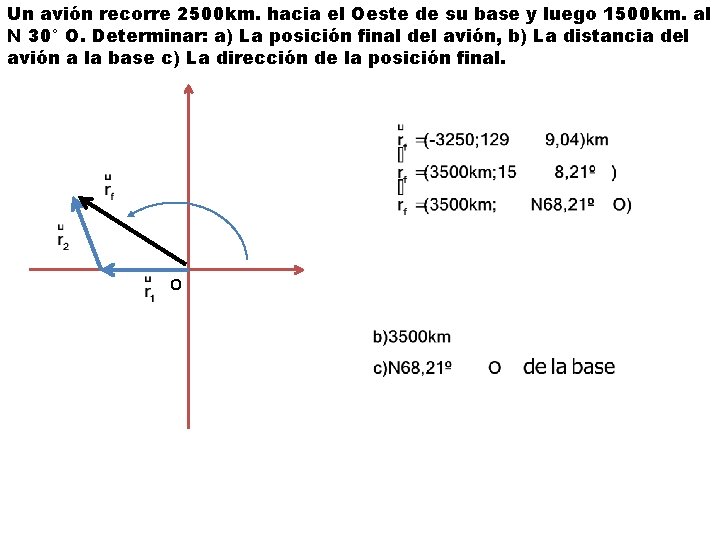
Un avión recorre 2500 km. hacia el Oeste de su base y luego 1500 km. al N 30° O. Determinar: a) La posición final del avión, b) La distancia del avión a la base c) La dirección de la posición final. O