Analisis Sensitivitas 1 Analisis Sensitivitas Bagaimana pengaruh perubahan

Analisis Sensitivitas 1

Analisis Sensitivitas • Bagaimana pengaruh perubahan data terhadap solusi optimum • Memberikan jawaban atas pertanyaan : – Sampai seberapa jauh perubahan dibenarkan tanpa mengubah solusi optimum atau tanpa menghitung solusi optimum dari awal 2

Analisis Sensitivitas • Kendala mana yang dapat dilonggarkan (dinaikkan) dan seberapa besar kelonggaran dapat diberikan sehingga menaikkan nilai z tetapi tanpa melakukan penghitungan dari awal. Kendala mana yang dapat diturunkan tanpa melakukan perhitungan dari awal • Kendala mana yang dapat prioritas untuk dinaikkan • Seberapa besar koefisien fungsi tujuan dapat dibenarkan untuk berubah tanpa mengubah solusi optimal 3

Contoh Soal: ü Perusahaan shader akan memprediksi barang andalaannya yaitu Ipod dan Jam-TV. Setiap Ipod membutuhkan 4 jam pengerjaan elektronik dan 2 jam perakitan. Jam-TV membutuhkan 3 jam pengerjaan elektronik dan 1 jam perakitan. Tersedia waktu 240 jam PE dam 100 jam perakitan. Setiap Ipod laba $7 dan Jam-TV $5 ü Hitung kombinasi optimum Jenis Pekerjaan Ipod Jam TV Max tersedia PE 4 2 240 P 3 1 100 4

Maksimumkan 7 X 1 + 5 X 2 Fungsi Kendala 4 X 1 + 3 X 2 ≤ 240 2 X 1 + X 2 ≤ 100 X 1 ≥ 0 X 2 ≥ 0 5
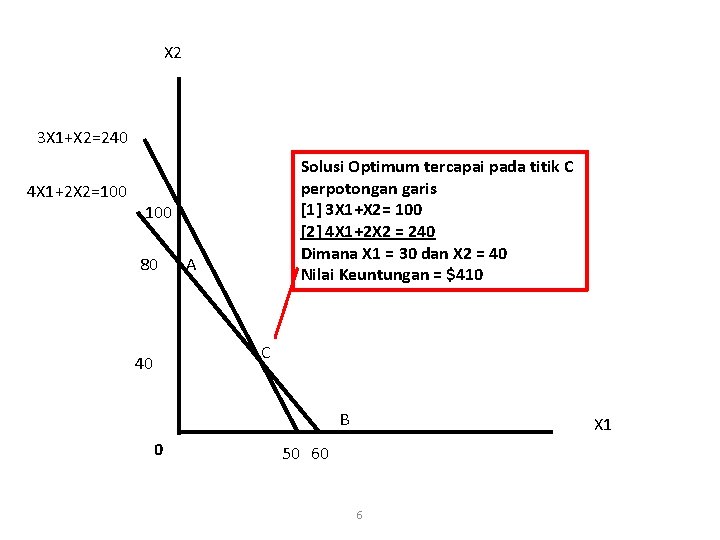
X 2 3 X 1+X 2=240 4 X 1+2 X 2=100 Solusi Optimum tercapai pada titik C perpotongan garis [1] 3 X 1+X 2= 100 [2] 4 X 1+2 X 2 = 240 Dimana X 1 = 30 dan X 2 = 40 Nilai Keuntungan = $410 100 80 A C 40 B 0 X 1 50 60 6
![X 2 2 X 1+X 2=110 Nilai Optimum pada titik C perpotongan garis [1] X 2 2 X 1+X 2=110 Nilai Optimum pada titik C perpotongan garis [1]](http://slidetodoc.com/presentation_image/33d8a68b2a6619d1813a523b8f53ad58/image-7.jpg)
X 2 2 X 1+X 2=110 Nilai Optimum pada titik C perpotongan garis [1] 2 X 1+X 2= 110 [2] 4 X 1+3 X 2 = 240 Dimana X 1 = 15 dan X 2 = 20 Nilai Keuntungan = $415 110 4 X 1+3 X 2=240 80 A C 40 Hambatan Jam PE tidak berubah B 0 X 1 60 7
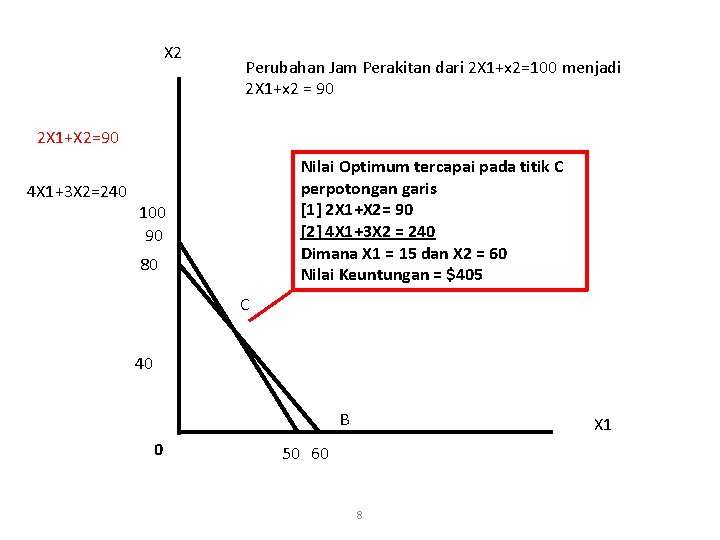
X 2 Perubahan Jam Perakitan dari 2 X 1+x 2=100 menjadi 2 X 1+x 2 = 90 2 X 1+X 2=90 4 X 1+3 X 2=240 Nilai Optimum tercapai pada titik C perpotongan garis [1] 2 X 1+X 2= 90 [2] 4 X 1+3 X 2 = 240 Dimana X 1 = 15 dan X 2 = 60 Nilai Keuntungan = $405 100 90 80 C 40 B 0 X 1 50 60 8

9
- Slides: 9