ANALISIS REGRESI KORELASI PENDAHULUAN Analisis regresi dan korelasi

ANALISIS REGRESI & KORELASI

PENDAHULUAN �Analisis regresi dan korelasi menyatakan hubungan antara dua variabel atau lebih. �Analisis regresi : menunjukkan bentuk hubungan antara dua variabel atau lebih persamaan regresi �Analisis korelasi : menunjukkan kekuatan hubungan antara dua variabel atau lebih koefisien korelasi

Dalam suatu persamaan regresi terdapat 2 macam variabel, yaitu : �Variabel dependen (variabel tak bebas) adalah variabel yang nilainya bergantung dari variabel lain. Biasanya dinyatakan dengan Y. �Variabel independen (variabel bebas) adalah variabel yang nilainya tidak bergantung dari variabel lain. Biasanya dinyatakan dengan X.

ANALISIS REGRESI �Regresi dikelompokkan menjadi 2 : 1. Regresi linier terdiri dari : a. Regresi linier sederhana : * 1 variabel tak bebas (dependent) dan 1 variabel bebas (independent). b. Regresi linier berganda * 1 variabel tak bebas dan lebih dari 1 variabel bebas 2. Regresi tak linier

Contoh penggunaan analisis regresi 1. Analisis Regresi antara tinggi orang tua terhadap 2. 3. 4. 5. 6. tinggi anaknya (Gultom). Analisis Regresi antara pendapatan terhadap konsumsi rumah tangga. Analisis Regresi antara harga terhadap penjualan barang. Analisis Regresi antara tingkat upah terhadap tingkat pengangguran. Analisis Regresi antara tingkat suku bunga bank terhadap harga saham Analisis regresi antara biaya periklanan terhadap volume penjualan perusahaan.

Langkah pertama dalam menganalisa relasi antar variabel adalah dengan membuat diagram pencar (scatter diagram) yang menggambarkan titik-titik plot dari data yang diperoleh. Diagram pencar ini berguna untuk : 1. membantu dalam melihat apakah ada relasi yang berguna antar variabel, 2. membantu dalam menentukan jenis persamaan yang akan digunakan untuk menentukan hubungan tersebut.

Linier positif Linier negatif

Curvelinier positif Curvelinier negatif

Analisis Regresi Linier Sederhana ØSuatu persamaan garis lurus yang menyatakan hubungan antara sebuah variabel bebas X dan sebuah variabel tidak bebas Y, dan digunakan untuk memperkirakan nilai Y berdasarkan nilai X disebut sebagai persamaan regresi

Metode kuadrat terkecil �Adalah suatu metode yang digunakan untuk menentukan persamaan linier estimasi �Kriteria ini dikenal dengan prinsip kuadrat terkecil (principle of least square). �Prinsip pemilihan garis regresi ini adalah “pilih garis yang mempunyai jumlah kuadrat deviasi nilai observasi Y terhadap nilai Y prediksinya yang minimum sebagai garis regresi yang paling baik”

Persamaan regresi estimasi yang baik secara umum dimana adalah nilai estimasi Y berdasarkan X yang dipilih. a adalah titik potong Y. b adalah kemiringan garis, X adalah sembarang nilai variabel bebas yang dipilih

�Nilai a dan b adalah :

Uji Koefisien regresi

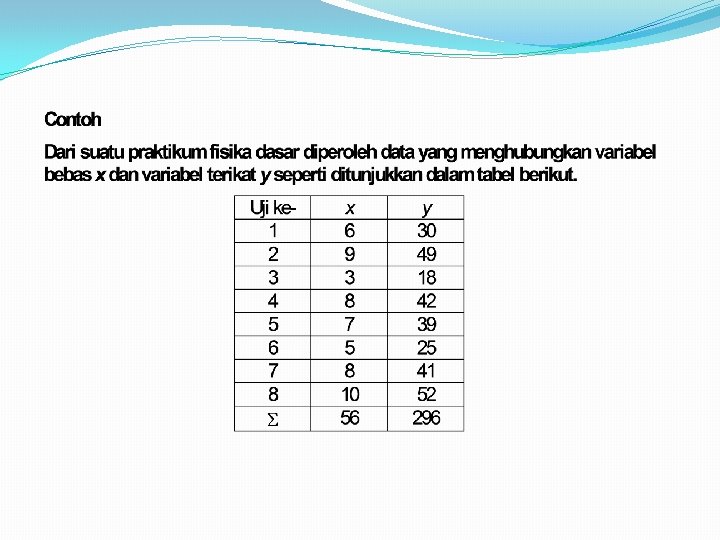
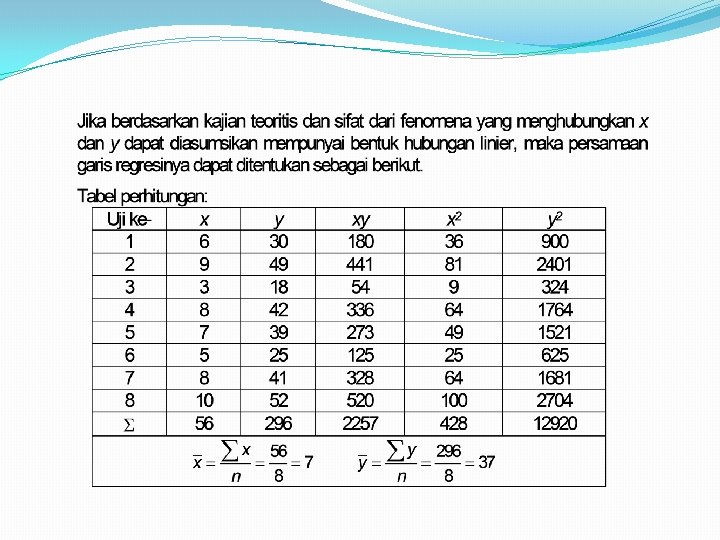
Contoh

Regresi Linier Berganda Model regresi linier berganda melibatkan lebih dari satu variabel bebas. Modelnya : Dimana Y = variabel terikat Xi = variabel bebas ( i = 1, 2, 3, …, k) 0 = intersep i = koefisien regresi ( i = 1, 2, 3, …, k) Model penduganya adalah 19

Regresi Linier Berganda Misalkan model regresi dengan kasus 2 peubah bebas X 1 dan X 2 maka modelnya : Sehingga setiap pengamatan Akan memenuhi persamaan 20

Menaksir Koefisien Regresi Dengan Menggunakan Matriks Dari hasil Metode Kuadrat Terkecil didapatkan persamaan normal : …. . 21

Menaksir Koefisien Regresi Dengan Menggunakan Matriks Tahapan perhitungan dengan matriks : 1. Membentuk matriks A, b dan g 22

Menaksir Koefisien Regresi Dengan Menggunakan Matriks 23

Menaksir Koefisien Regresi Dengan Menggunakan Matriks 2. Membentuk persamaan normal dalam bentuk matriks Ab=g 3. Perhitungan matriks koefisien b b = A-1 g 24

Metode Pendugaan Parameter Regresi Dengan Metode Kuadrat Terkecil, misalkan model terdiri dari 2 variabel bebas Tahapan pendugaannya : 1. Dilakukan turunan pertama terhadap b 0 , b 1 dan b 2 25

Metode Pendugaan Parameter Regresi 2. Ketiga persamaan hasil penurunan disamakan dengan nol 26

Metode Pendugaan Parameter Regresi 3. Nilai b 1 dan b 2 dapat diperoleh dengan memakai aturan-aturan dalam matriks 27

Uji Kecocokan Model 1. Dengan Koefisien Determinasi R 2 menunjukkan proporsi variasi total dalam respon Y yang dapat diterangkan oleh model r merupakan koefisien korelasi antara Y dengan kelompok X 1 , X 2 , X 3 , … , Xk 28

Uji Kecocokan Model 2. Dengan Pendekatan Analisis Ragam Tahapan Ujinya : 1. Hipotesis = H 0 : 0 H 1 : 0 dimana = matriks [ 0, 1, 2, … , k ] 29

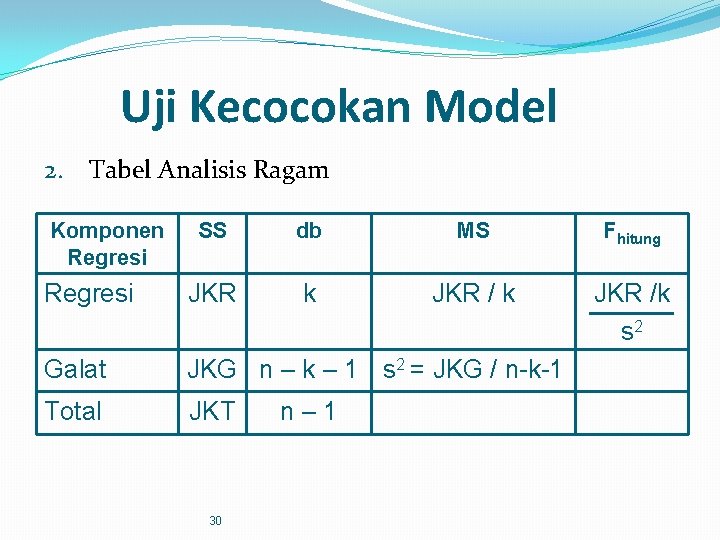
Uji Kecocokan Model 2. Tabel Analisis Ragam Komponen Regresi SS db MS Fhitung Regresi JKR k JKR /k s 2 Galat JKG n – k – 1 s 2 = JKG / n-k-1 Total JKT 30 n– 1

Uji Kecocokan Model 3. Pengambilan Keputusan H 0 ditolak jika Fhitung pada taraf kepercayaan > Ftabel(1 , n-k-1) 31

Uji Parsial Koefisien Regresi Tahapan Ujinya : 1. Hipotesis = H 0 : j 0 H 1 : j 0 dimana j merupakan koefisien yang akan diuji 32

Uji Parsial Koefisien Regresi 2. Statistik uji : Dimana : bj = nilai koefisien bj s = cjj = nilai matriks A-1 ke-jj 33

Uji Parsial Koefisien Regresi 3. Pengambilan keputusan H 0 ditolak jika thitung pada taraf kepercayaan > t /2(db= n-k-1) 34

Pemilihan Model Terbaik 1. All Possible Regression Tahapan pemilihan : i. Tuliskan semua kemungkinan model regresi dan kelompokkan menurut banyaknya variabel bebas ii. Urutkan model regresi menurut besarnya R 2 iii. Periksalah untuk setiap kelompok apakah terdapat suatu pola variabel yang konsisten iv. Lakukan analisa terhadap kenaikan R 2 pada tiap kelompok 35

Pemilihan Model Terbaik Contoh : Akan dianalisis model regresi yang terdiri dari 4 variabel bebas Pembagian kelompoknya Kelompok A terdiri dari koefisien intersep Kelompok B terdiri dari 1 variabel bebas Kelompok C terdiri dari 2 variabel bebas Kelompok D terdiri dari 3 variabel bebas Kelompok E terdiri dari 4 variabel bebas 36

Pemilihan Model Terbaik Persamaan regresi yang menduduki posisi utama dalam setiap kelompok adalah Kelompok Model Regresi B Y = f(X 4) C Y = f(X 1 , X 2) Y = f(X 1 , X 4) D Y = f(X 1 , X 2 , X 4) E Y = f(X 1 , X 2 , X 3, X 4) R 2 67, 5% 97, 9% 97, 2% 98, 234% 98, 237% Persamaan terbaiknya adalah Y = f(X 1 , X 4) 37

Pemilihan Model Terbaik 2. Backward Elimination Procedur Tahap pemilihannya : i. Tuliskan persamaan regresi yang mengandung semua variabel ii. Hitung nilai t parsialnya iii. Banding nilai t parsialnya a. b. Jika t. L < t. O maka buang variabel L yang menghasilkan t. L, kemudian hitung kembali persamaan regresi tanpa menyertakan variabel L Jika t. L > t. O maka ambil persamaan regresi tersebut 38

Pemilihan Model Terbaik Contoh : Akan dianalisis model regresi yang terdiri dari 4 variabel bebas Model regresi yang mengandung semua variabel bebas Persamaan Regersi t parsial Y = f(X 1, X 2, X 3, X 4) Model terbaiknya Y = f(X 1, X 2) 157, 266* X 1 4, 337* X 2 0, 497* X 3 0, 018 X 4 0, 041* Y = f(X 1, X 2, X 4) Y = f(X 1, X 2) 39 F 166, 83* X 1 154, 008* X 2 5, 026* X 4 1, 863 229, 5*

Pemilihan Model Terbaik 3. Stepwise Regression Procedur Tahap pemilihannya : i. Hitung korelasi setiap variabel bebas terhadap variabel Y. Variabel bebas dengan nilai korelasi tertinggi masukkan dalam model regresi (syarat uji F menunjukkan variabel ini berpengaruh nyata) ii. Hitung korelasi parsial setiap variabel bebas tanpa menyertakan variabel bebas yang telah mauk model. Masukkan variabel bebas dengan korelasi parsial tertinggi ke dalam model iii. Hitung nilai t parsial variabel yang telah masuk model, jika tidak berpengaruh nyata keluarkan dari model iv. Kembali ke langkah ii 40

Pemilihan Model Terbaik Contoh : Akan dianalisis model regresi yang terdiri dari 4 variabel bebas 41

Model Variabel Korelasi riy 0, 731 r 2 y 0, 816 r 3 y -0, 535 r 4 y -0, 821 t parsial Y = f(X 4) Model terbaik Y = f(X 1 , X 2) F 22, 798* r 1 y. 4 0, 915 r 2 y. 4 0, 017 r 3 y. 4 0, 801 Y = f(X 1, X 4) 176, 627* r 2 y. 14 0, 358 X 1 = 108, 223* r 3 y. 14 0, 320 X 4 = 159, 295* Y = f(X 1, X 2, X 4) 166, 832* X 1 = 154, 008* X 2 = 5, 026* X 4 = 1, 863 r 3 y. 124 Y = f(X 421, X 2) 0, 002 229, 504*

Regresi Linear Non Linear Regresi Linear

Analisis Korelasi

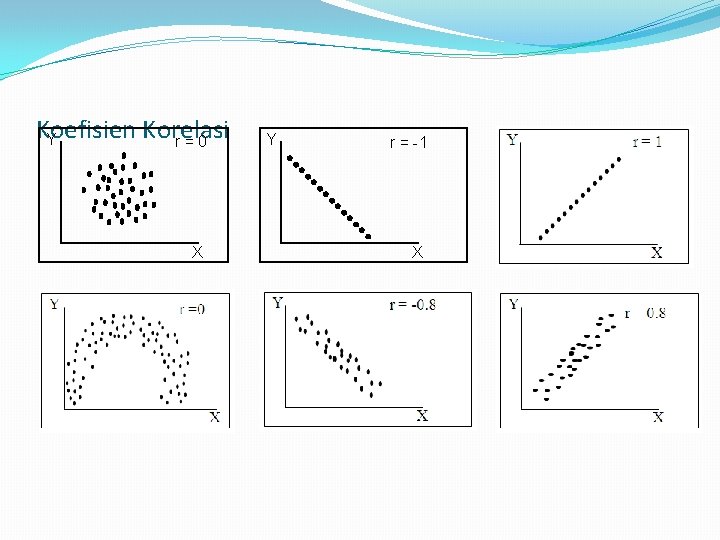
Koefisien Korelasi Arti besar nilai r � Jika r = 1 atau mendekati 1 maka hubungan antara 2 variabel sangat kuat secara positif yaitu hubungan yang terjadi searah yaitu apabila nilai X meningkat maka Y juga akan semakin meningkat dan sebaliknya. � Jika r = -1 atau mendekati -1 maka hubungan antara 2 variabel sangat kuat secara negatif yaitu hubungan yang terjadi berbalik arah yaitu apabila nilai X meningkat maka akan diikuti dengan penurunan Y atau sebaliknya. � Jika r = 0 atau mendekati 0 maka hubungan antara 2 variabel tidak ada atau lemah maka dapat dikatakan tidak terdapat hubungan antara X dan Y.

Berdasarkan nilai derajat korelasinya baik positif maupun negatif adalah : ü 0, 7 – 1 : Kuat/erat ü 0, 4 – 0, 7 : Sedang ü 0, 2 – 0, 4 : Rendah ü < 0, 2 : Lemah atau diabaikan dianggap tidak adanya hubungan antar 2 variabel

Koefisien Korelasi Y r=0 X Y r = -1 X

Uji Korelasi

Contoh