Analisis Korelasional ANALISIS KORELASI Analisis korelasi merupakan salah

Analisis Korelasional

ANALISIS KORELASI Analisis korelasi merupakan salah satu teknik statistik yang digunakan untuk menganalisis hubungan antara dua variabel atau lebih yang bersifat kuantitatif.

Analisis Korelasi • Korelasi merupakan angka yang menunjukkan arah dan kuatnya hubungan antar dua variabel atau lebih. • Hubungan antar dua variable disebut dengan bivariate correlation. • Hubungan antar lebih dari dua variable disebut dengan multivariate correlation. • Ditemukan oleh Karl Pearson (awal 1900) sehingga disebut Korelasi Pearson Product Moment (PPM)

• Korelasi digunakan sebagai teknik analisis yang termasuk dalam kelompok pengukuran hubungan atau asosiasi (measures of association). • Di antara sekian banyak teknik-teknik pengukuran asosiasi, terdapat dua teknik korelasi yang sangat populer yaitu Korelasi Pearson Product Moment dan Korelasi Rank Spearman. • Selain kedua teknik tersebut, terdapat pula teknik-teknik korelasi lain, seperti Kendal, Chi. Square, Phi Coefficient, Goodman-Kruskal, Somer, dan Wilson.

Arah Korelasi • Arah dinyatakan dalam bentuk korelasi positif (+) dan korelasi negatif (-). • Kuatnya hubungan dinyatakan dengan besarnya koefisien korelasi (r). • Korelasi positif, yaitu jika dua variable yang berkorelasi berjalan paralel; menunjukkan arah yang sama. • Korelasi negatif, yaitu dua variable yang berkorelasi berjalan dengan arah yang berlawanan.

Kapan suatu variabel dikatakan saling berkorelasi ? Variabel dikatakan saling berkorelasi jika perubahan suatu variabel diikuti dengan perubahan variabel yang lain.

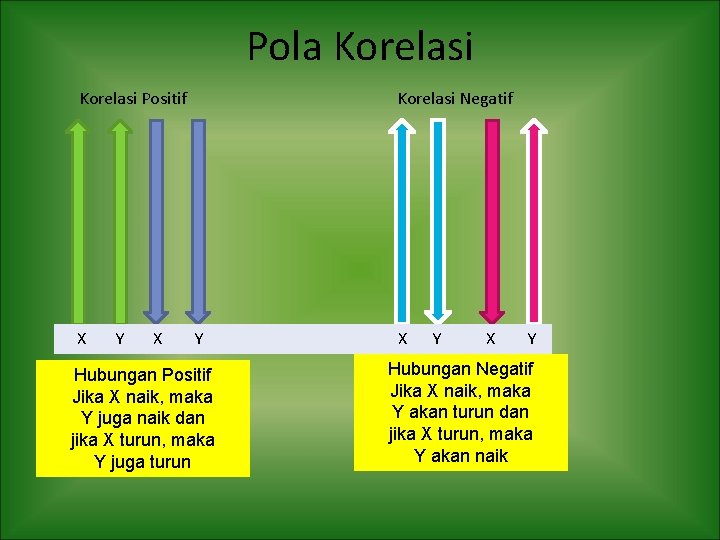
Pola Korelasi Positif Korelasi Negatif X Y X Y X Y Hubungan Positif Jika X naik, maka Y juga naik dan jika X turun, maka Y juga turun Hubungan Negatif Jika X naik, maka Y akan turun dan jika X turun, maka Y akan naik

Macam-Macam Teknik Korelasi • Pearson Product Moment (r) adalah teknik yang paling banyak digunakan khusus-nya untuk mendapatkan standar kesalahan terkecil (interval) • Rank Spearman ( ), sering dipakai sebagai pengganti product moment terutama jika sampel kurang dari 30 (ordinal-ordinal) • Tau Kendal ( ), sering dipakai sebagai pengganti PPM dan Rank Spearman terutama jika sampel sangt kecil (n < 10) (ordinal-ordinal)

Sifat Penting Korelasi 1. Koefisien korelasi populasi dinotasikan dengan (rho) sedangkan koefisien korelasi sampel dinotasikan dengan r. 2. Koefisien korelasi bernilai antara -1 sampai +1 3. Koefisien korelasi bersifat simetrik koefisien korelasi X dan Y sama dengan koefisien korelasi Y dan X 4. Jika X dan Y yang diamati adalah dua variabel yang saling bebas maka rxy = 0. 5. Koefisien korelasi mengukur derajat hubungan dan tidak dapat diinterpretasikan sebagai hubungan kausal (sebabakibat). 6. Korelasi digunakan untuk mengukur keterkaitan dua variabel yang secara teoritis dibenarkan.

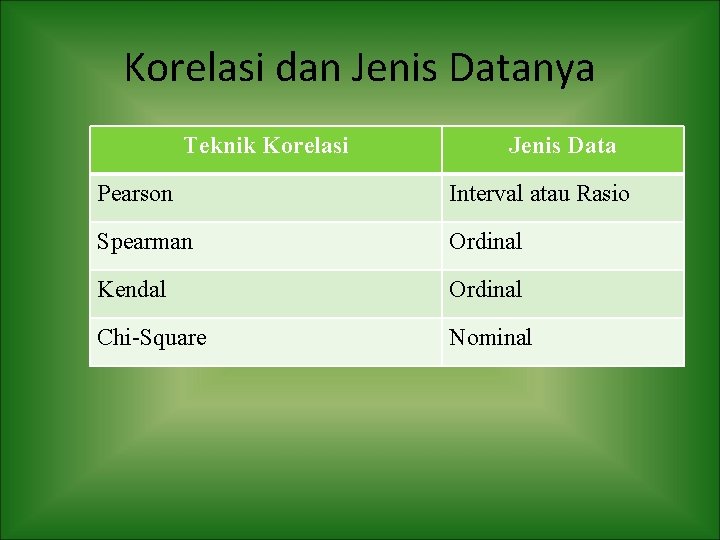
Korelasi dan Jenis Datanya Teknik Korelasi Jenis Data Pearson Interval atau Rasio Spearman Ordinal Kendal Ordinal Chi-Square Nominal

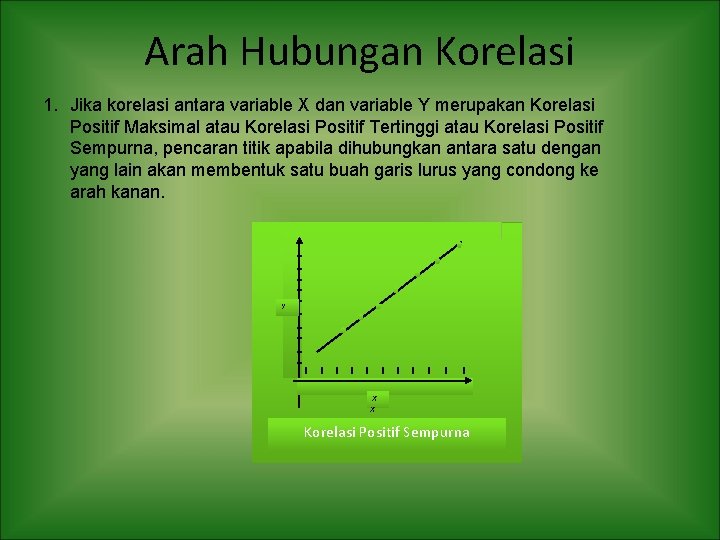
Arah Hubungan Korelasi 1. Jika korelasi antara variable X dan variable Y merupakan Korelasi Positif Maksimal atau Korelasi Positif Tertinggi atau Korelasi Positif Sempurna, pencaran titik apabila dihubungkan antara satu dengan yang lain akan membentuk satu buah garis lurus yang condong ke arah kanan. Y X X Korelasi Positif Sempurna

2. Jika korelasi antra variable X dan Varibale Y merupakan Korelasi Negatif Maksimal atau Korelasi Negatif Tertinggi atau Korelasi Negatf Sempurna, maka pencaran titik apabila dihubungkan satu sama yang lain akan membentuk satu buah garis luurs yang condong ke arah kiri. Y Y X X Korelasi Negatif Sempurna

3. Jika korelasi antara variable X dan variable Y merupakan Korelasi Positif Yang Tinggi atau Kuat, maka pencaran titiknya sedikit menjauhi garis linear (lurus), yaitu titik tersebut terpencar atau berada di sekitar garis lurus tersebut dengan kecondongan ke arah kanan. Y X X Korelasi Positif Tinggi

4. Jika korelasi antara variable X dan variable Y merupakan Korelasi Negatif Yang Tinggi atau Kuat, maka pencaran titiknya sedikit menjauhi garis linear (lurus), yaitu titik tersebut terpencar atau berada di sekitar garis lurus tersebut dengan kecondongan ke arah kiri. Y X X Korelasi Negatif Tinggi

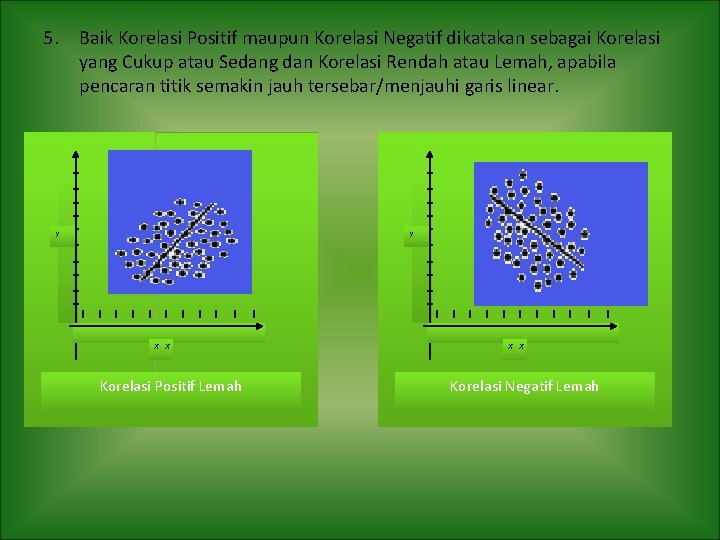
5. Baik Korelasi Positif maupun Korelasi Negatif dikatakan sebagai Korelasi yang Cukup atau Sedang dan Korelasi Rendah atau Lemah, apabila pencaran titik semakin jauh tersebar/menjauhi garis linear. Y Y X X Korelasi Positif Lemah X X Korelasi Negatif Lemah

Teknik Korelasi Product Moment • Teknik Korelasi Product Moment merupakan salah satu teknik mencari korelasi antar dua variable. • Disebut Product Moment Correlation karena koefisien korelasinya diperoleh dengan cara mencari hasil perkalian dari momen-momen variable yang dikorelasikan.

Kapan digunakan Korelasi Product Moment? 1. Variable yang dikorelasikan berbentuk gejala atau data yang bersifat continue. 2. Sampel yang diteliti mempunyai sifat homogen atau setidak-tidaknya mendekati homogen. 3. Regresinya merupakan regresi linear.

Kuat dan tidaknya hubungan antara X dan Y apabila dapat dinyatakan dengan fungsi linear(paling tidak mendekati), diukur dengan suatu nilai yang disebut koefisien korelasi. Nilai koefisien korelasi ini paling sedikit – 1 dan paling besar +1. Jadi jika r = koefisien korelasi, maka r dapat dinyatakan sebagai berikut : -1 r +1 Kuat (-) Kuat (+) +1 -1 Lemah (-) Jika Lemah (+) r =+1, hubungan X dan Y sempurna dan positif, r = -1, hubungan X dan Y sempurna dan negatif, r mendekati +1, hubungan sangat kuat dan positif, r mendekati – 1, hubungan sangat kuat dan negatif.

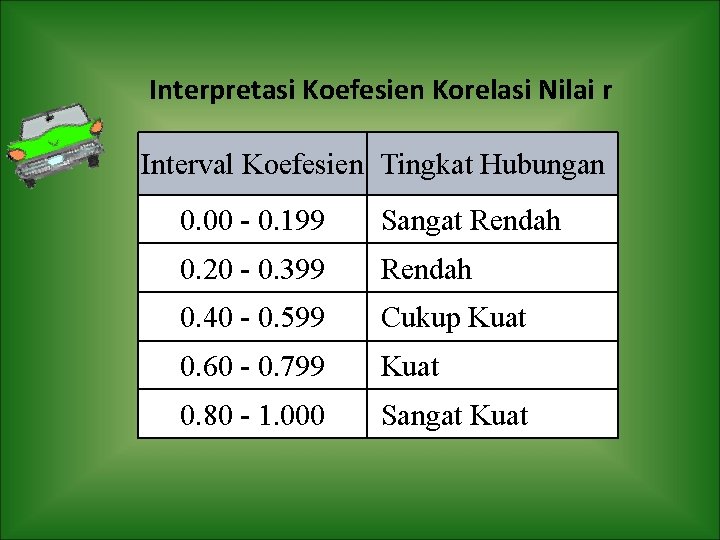
Interpretasi Koefesien Korelasi Nilai r Interval Koefesien Tingkat Hubungan 0. 00 - 0. 199 Sangat Rendah 0. 20 - 0. 399 Rendah 0. 40 - 0. 599 Cukup Kuat 0. 60 - 0. 799 Kuat 0. 80 - 1. 000 Sangat Kuat

Cara Mencari Angka Indeks Korelasi Product Moment Koefesien Korelasi product Moment dapat diperoleh dengan rumus:

Contoh: • apakah secara signifikan terdapat korelasi positif antara Motivasi (X) dengan Kinerja Dosen (Y) S 1 IP Fakultas Adab dan Humaniora UIN Ar. Raniry? • Hasil penelitian menunjukkan data seperti berikut. X Y 60 40 35 30 40 50 60 40 30 55 50 50 130 100 125 140 120 150 120 130 140 150 130 • Untuk menyelesaikannya dilakukan seperti berikut. 1. Membuat Hipotesis research Ha dan Hipotesis Ho dalam bentuk kalimat: Ha # terdapat hubungan yang signifikan antara motivasi dengan kinerja dosen. Ho = tidak terdapat hubungan yang signifikan antara motivasi dengan kinerja dosen. 2. Membuat hipotesis statistik: Ha : r # 0 Ho : r = 0

Penyelesaian - lanjut 3. Membuat tabel penolong untuk menghitung korelasi product Moment No X Y X 2 1 2 3 4 5 6 7 8 9 10 11 12 60 40 35 30 40 50 60 40 30 55 50 50 540 150 130 100 125 140 120 150 120 130 140 150 130 1585 3600 1225 900 1600 2500 3600 1600 900 3025 2500 25550 Y 2 XY 22500 9000 16900 5200 10000 3500 15625 3750 19600 5600 14400 6000 22500 9000 14400 4800 16900 3900 19600 7700 22500 7500 16900 6500 211825 72450

Lanjutan 4. Mencari rhitung dengan cara memasukkan angka statistik dari tabel di atas ke dalam rumus rxy product moment.

Lanjutan 5. Mencari besar kontribusi variable X terhadap variable Y dengan rumus: Ini artinya motivasi hanya memberikan kontribusi terhadap kinerja dosen sebesar 40. 94% dan sisanya ditentukan oleh variable lain.

Lanjutan 6. Untuk mengetahui signifikan atau tidak, maka dilakukan dengan rumus berikut:

Interpretasi Secara Kasar atau Sederhana Dari perhitungan di atas, telah diketahui rxy sebesar 0. 6399. Ini berarti hasilnya positif, dengan demikian korelasi antara variable X dan Variable Y terdapat hubungan yang searah atau dengan istilah lain: terdapat korelasi positif. Dari angka tersebut (0. 6399), jika dilihat indek korelasi, maka terletak antara 0. 60 -0. 80. Ini berarti, korelasi antara variable X dan variable Y adalah tergolong Kuat.

Interpretasi dengan menggunakan Tabel Nilai r Product Moment • Langkah 1 Lihat kembali rumusan hipotesis di atas.

Interpretasi - Lanjutan Langkah 2: mencari df – degree of freedom Kaidah pengujian: Jika thitung ≥ ttabel, maka Ho ditolak. Artinya korelasinya signifikan. Jika thitung ≤ ttabel, Ho diterima. Artinya korelasinya tidak signifikan. Untuk mencari ttable, maka dicari df, yaitu df=n-2=12 -2=10 sehingga diperoleh ttable pada taraf signifikan α=0. 05 adalah 2. 228. kemudian thitung tersebut dibandingkan dengan ttabel dan ternyata thitung > dari ttable (3. 363 >2. 228), maka Ho ditolak. Dengan demikian ada hubungan yang signifikan antara motivasi dengan kinerja dosen.

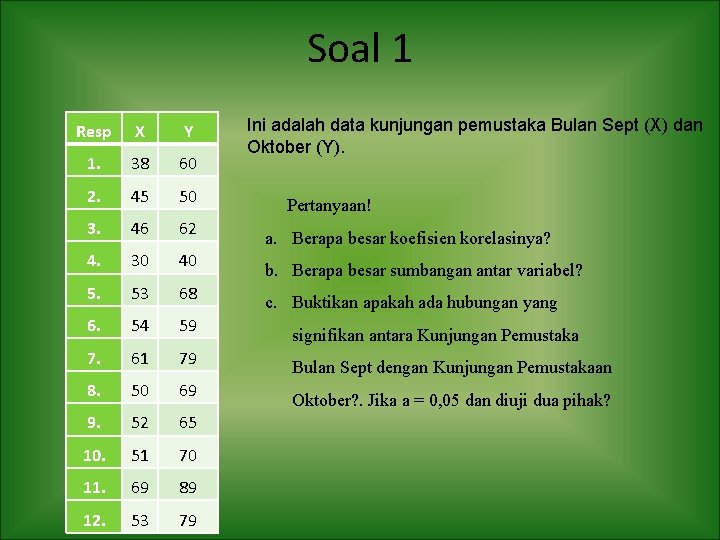
Soal 1 Ini adalah data kunjungan pemustaka Bulan Sept (X) dan Oktober (Y). Resp X Y 1. 38 60 2. 45 50 3. 46 62 a. Berapa besar koefisien korelasinya? 4. 30 40 b. Berapa besar sumbangan antar variabel? 5. 53 68 c. Buktikan apakah ada hubungan yang 6. 54 59 signifikan antara Kunjungan Pemustaka 7. 61 79 Bulan Sept dengan Kunjungan Pemustakaan 8. 50 69 Oktober? . Jika a = 0, 05 dan diuji dua pihak? 9. 52 65 10. 51 70 11. 69 89 12. 53 79 Pertanyaan!

Contoh Kasus: Makcik Nurul Fajar melakukan survei untuk meneliti apakah ada korelasi antara pendapatan mingguan dan besarnya tabungan mingguan di Tungkop? Untuk menjawab permasalahan tersebut Nurul ambil sampel sebanyak 10 kepala keluarga.

Data Yang dikumpulkan Tabungan 2 4 6 6 8 8 9 10 Pendapatan 10 20 50 55 60 65 75 70 81 85 Kriteria: Ho diterima Jika r hitung ≤ r tabel( , n-2) atau t hitung ≤ t tabel ( , n-2) Ha diterima Jika r hitung > r tabel( , n-2) atau t hitung > t tabel ( , n-2)

KOEFISIEN KORELASI GANDA Khatib A. Latief Email: kalatief@gmail. com; khatibalatif@yahoo. com Twitter: @khatibalatief Khatib A. Latief Mobile: +628 1168 3019

Pengantar v Berkenaan dengan hubungan tiga atau lebih variable v Sekurang-kurangnya dua variabel independen dihubungkan dengan variabel dependennya v Dalam korelasi ganda koefisien korelasinya dinyatakan dalam R. v Analisis Korelasi Ganda berfungsi untuk mencari besar hubungan dan kontribusi dua variabel independen (X) atau lebih secara simultan (bersama-sama) dengan variable dependen (Y). 33

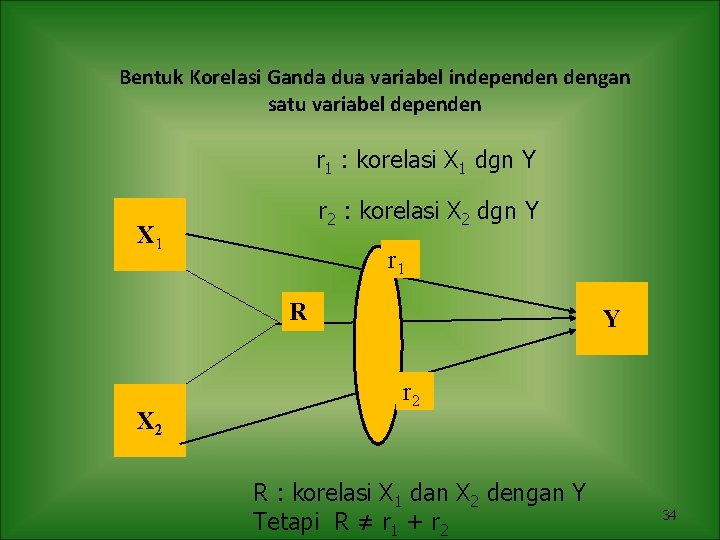
Bentuk Korelasi Ganda dua variabel independen dengan satu variabel dependen r 1 : korelasi X 1 dgn Y r 2 : korelasi X 2 dgn Y X 1 r 1 R X 2 Y r 2 R : korelasi X 1 dan X 2 dengan Y Tetapi R ≠ r 1 + r 2 34

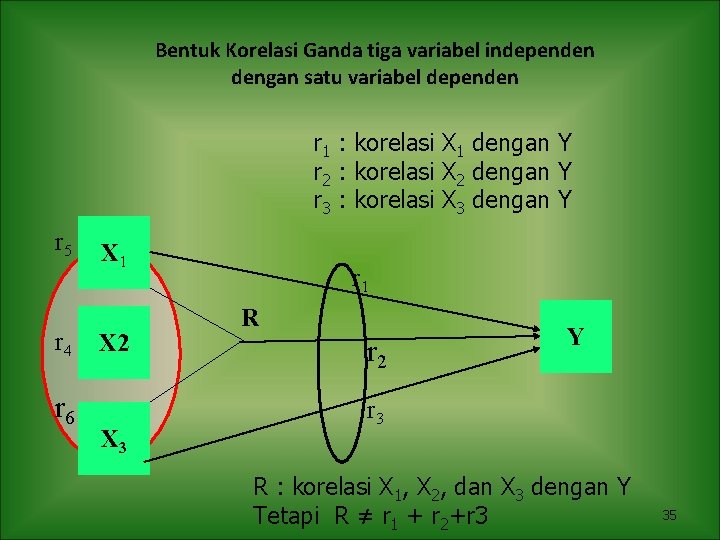
Bentuk Korelasi Ganda tiga variabel independen dengan satu variabel dependen r 1 : korelasi X 1 dengan Y r 2 : korelasi X 2 dengan Y r 3 : korelasi X 3 dengan Y r 5 r 4 r 6 X 1 X 2 X 3 r 1 R r 2 Y r 3 R : korelasi X 1, X 2, dan X 3 dengan Y Tetapi R ≠ r 1 + r 2+r 3 35

• Rumus Korelasi Ganda (dua variable independen) 36

Langkah-langkah menghitung Korelasi Ganda 1. Jika harga r belum diketahui, maka hitunglah harga r. Biasanya sudah ada karena kelanjutan dari korelasi tunggal. 2. hitunglah rhitung dengan rumus sebagai berikut : untuk dua variabel bebas : 37

Langkah-langkah…continued 3. tetapkan taraf signifikansi (α), sebaiknya disamakan dengan α terdahulu; 4. Rumuskan hipotesis, yaitu : a. Membuat hipotesis riset Ha dan Ho; Ha = terdapat hubungan yang signifikan antara X 1, X 2 dengan Y Ho = tidak terdapat yang signifikan antara X 1, X 2 dengan Y b. Buat hipotesis statistik: • Ha : Ryx 1 x 2 ≠ 0 • H 0 : Ryx 1 x 2 = 0 5. Tentukan kriteria R, yaitu: Jika Fhitung ≤ Ftabel maka H 0 diterima 38

Langkah-langkah …continued • 39

Langkah-langkah…continued 7. Cari Ftabel = F(1 -α), kemudian dengan dkpembilang = k dkpenyebut = n-k-1 di mana k = banyaknya variabel bebas n = banyaknya anggota sampel dengan melihat tabel f didapat nilai ftabel 9. Bandingkan fhitung dan ftabel 10. Buat kesimpulannya 40

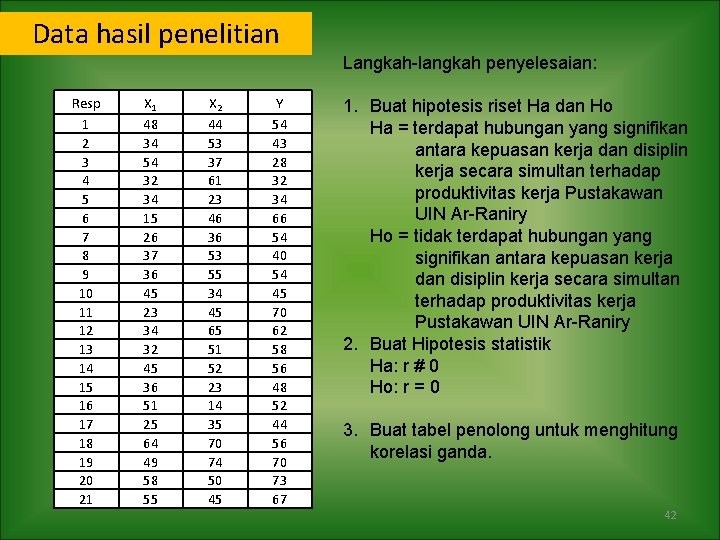
Contoh Judul Penelitian: Korelasi Kepuasan Kerja dan Disiplin Kerja Terhadap Produktivitas Kerja Pustakawan UIN Ar-Raniry Dari judul tersebut diketahui bahwa penelitian ini memiliki tiga variabel, yaitu: 1. Variabel X 1 – Kepuasan Kerja 2. Variable X 2 – Disiplin Kerja 3. Variabel Y – Produktivitas Kerja Untuk mendapatkan data dilakukan penelitian terhadap 21 Pustakawan UIN Ar-Raniry dengan taraf sigfinifkan 5%. Hasil penelitian ditemukan data seperti berikut. 41

Data hasil penelitian Langkah-langkah penyelesaian: Resp 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 X 1 48 34 54 32 34 15 26 37 36 45 23 34 32 45 36 51 25 64 49 58 55 X 2 44 53 37 61 23 46 36 53 55 34 45 65 51 52 23 14 35 70 74 50 45 Y 54 43 28 32 34 66 54 40 54 45 70 62 58 56 48 52 44 56 70 73 67 1. Buat hipotesis riset Ha dan Ho Ha = terdapat hubungan yang signifikan antara kepuasan kerja dan disiplin kerja secara simultan terhadap produktivitas kerja Pustakawan UIN Ar-Raniry Ho = tidak terdapat hubungan yang signifikan antara kepuasan kerja dan disiplin kerja secara simultan terhadap produktivitas kerja Pustakawan UIN Ar-Raniry 2. Buat Hipotesis statistik Ha: r # 0 Ho: r = 0 3. Buat tabel penolong untuk menghitung korelasi ganda. 42

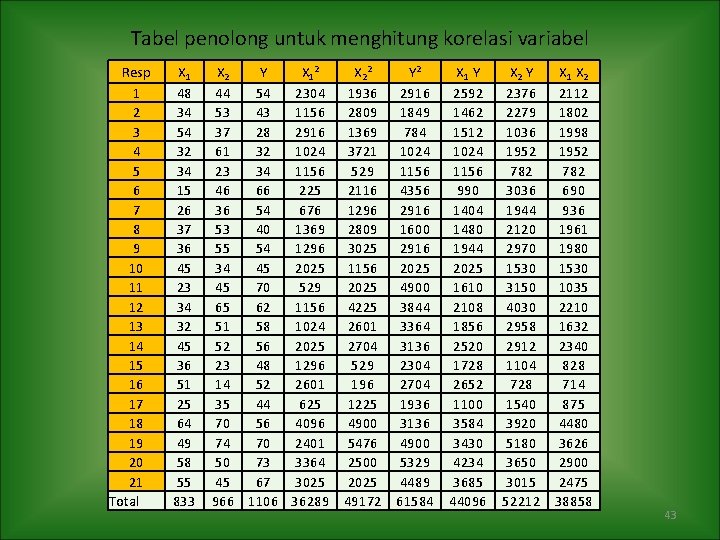
Tabel penolong untuk menghitung korelasi variabel Resp 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Total X 1 48 34 54 32 34 15 26 37 36 45 23 34 32 45 36 51 25 64 49 58 55 833 X 2 Y X 12 X 22 Y 2 44 54 2304 1936 2916 53 43 1156 2809 1849 37 28 2916 1369 784 61 32 1024 3721 1024 23 34 1156 529 1156 46 66 225 2116 4356 36 54 676 1296 2916 53 40 1369 2809 1600 55 54 1296 3025 2916 34 45 2025 1156 2025 45 70 529 2025 4900 65 62 1156 4225 3844 51 58 1024 2601 3364 52 56 2025 2704 3136 23 48 1296 529 2304 14 52 2601 196 2704 35 44 625 1225 1936 70 56 4096 4900 3136 74 70 2401 5476 4900 50 73 3364 2500 5329 45 67 3025 2025 4489 966 1106 36289 49172 61584 X 1 Y 2592 1462 1512 1024 1156 990 1404 1480 1944 2025 1610 2108 1856 2520 1728 2652 1100 3584 3430 4234 3685 44096 X 2 Y X 1 X 2 2376 2112 2279 1802 1036 1998 1952 782 3036 690 1944 936 2120 1961 2970 1980 1530 3150 1035 4030 2210 2958 1632 2912 2340 1104 828 714 1540 875 3920 4480 5180 3626 3650 2900 3015 2475 52212 38858 43

4. Hitung nilai korelasi X 1 terhadap Y 44

5. Hitung nilai korelasi X 2 terhadap Y 45

6. Hitung nilai korelasi X 1 terhadap X 2 46

6. Cari korelasi ganda 7. Masukkan hasil nilai tadi ke dalam rumus korelasi ganda Dari hasil korelasi ganda di atas menunjukkan bahwa korelasi antara kepuasan kerja dan disiplin kerja secara silmultan terhadap produktivitas kinerja pustakawan UIN Ar-Raniry tergolong rendah. 47

Kontribusi secara silmutan: - R 2 x 100% = 0. 33702 X 100% =11. 36%. - Sementara sisanya 84. 64% ditentukan oleh variabel lain. 8. Menguji signifikansi dengan rumus Fhitung 48

Kaidahnya: v Jika Fhitung ≤ Ftabel, maka Ho diterima. Dengan demikian hubungan antar variabel tidak signifikan. v Pada taraf signifikan α = 0. 05 Ftabel = F{(1 -α)(df=k), (df= n-2 -1)} Ftabel = F{(1 -0. 05)(df=2), (df= n-2 -1)} Ftabel = F{(0. 95), (2, 18) 49

• - Cara mencari Ftabel: Angka 2 sebagai angka pembilang Angka 18 sebagai angka penyebut Dengan demikian Ftabel=3. 98 9. Buat kesimpulan Nilai tersebut selanjutnya dibandingkan dengan nilai Fhitung yang sudah diperoleh sebelunya. Ternyata nilai Fhitung 1. 15 < Ftabel 3. 98. Dengan demikian Ho diterima dan Ha ditolak. Jadi koefesien korelasi ganda yang ditemukan tidak signifikan. 50

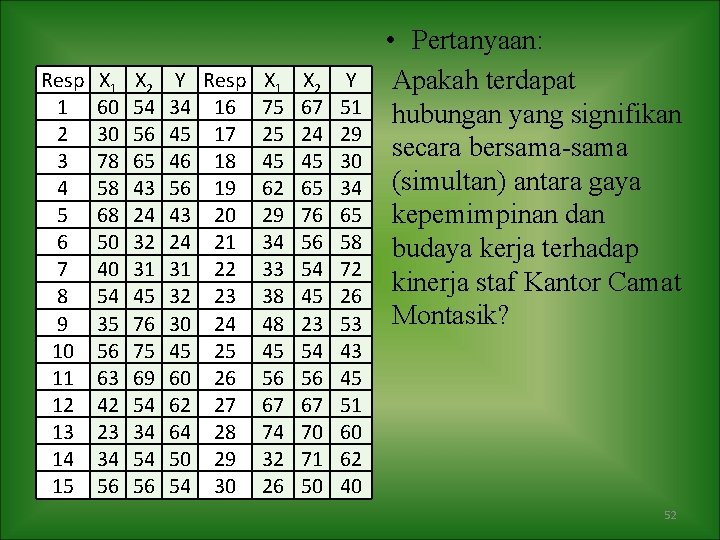
Tugas 1 Iklim melakukan penelitian di Montasik untuk mengetahui apakah ada korelasi antara gaya kepemimpinan Pak Camat (X 1) dan budaya kerja (X 2) terhadap Kinerja Staf (Y) Kantor Camat Montasik. Iklim mengedarkan angket kepada 30 pegawai secara random dan diperoleh data sebagai berikut. 51

Resp 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 X 1 60 30 78 58 68 50 40 54 35 56 63 42 23 34 56 X 2 54 56 65 43 24 32 31 45 76 75 69 54 34 54 56 Y Resp X 1 X 2 Y 34 16 75 67 51 45 17 25 24 29 46 18 45 45 30 56 19 62 65 34 43 20 29 76 65 24 21 34 56 58 31 22 33 54 72 32 23 38 45 26 30 24 48 23 53 45 25 45 54 43 60 26 56 56 45 62 27 67 67 51 64 28 74 70 60 50 29 32 71 62 54 30 26 50 40 • Pertanyaan: Apakah terdapat hubungan yang signifikan secara bersama-sama (simultan) antara gaya kepemimpinan dan budaya kerja terhadap kinerja staf Kantor Camat Montasik? 52

Tugas 2 Asmaul Husna ingin mengetahui hubungan antara variabel lama persahabatan (X 1); motivasi bersahabat (X 2) dan Kualitas Persahabatan (Y) Mahasiswa/I Angkatan 2015 FAH UIN Ar-Raniry. Data yang berhasil dihimpun berskala interval dari sampel yang diambil secara random. Data terdistribusi sbb: Resp 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Y X 1 X 2 13 50 60 17 41 16 12 23 30 32 30 21 23 51 30 24 26 15 18 19 10 17 17 21 25 19 45 26 32 11 54 23 16 19 24 13 21 31 20 14 32 30 15 50 18 39 43 24 54 40 20 Berdasarkan data tersebut tentukan: a. Berapa besar koefien korelasi berganda antar variabel tersebut? b. Berapa besar sumbangan variabel X 1 dan X 2 terhadap variabel Y? c. Bagaimana interpretasi yang dapat dikemukakan berdasarkan koefisien korelasi berganda yang telah dihitung?