Analisis Data Statistik Deskriptif Ukuran Gejala Pusat Ukuran

Analisis Data Statistik Deskriptif Ukuran Gejala Pusat Ukuran Letak

Analisis Data • Ukuran Pemusatan Data ü Ukuran Gejala Pusat : Rata-rata hitung, rata-rata ukur, rata-rata harmonik, Modus ü Ukuran Letak: Median, Kuartil, Desil, Presentil • Ukuran Simpangan/Penyebaran Data ü rentang, rentang antar kuartil, simpangan kuartil, deviasi rata-rata (rata-rata simpangan), varians, standar deviasi (simpangan baku), koefisien variasi. • Ukuran Kemiringan Data (Skewness) • Ukuran Tinggi Rendah Data (Kurtosis)

Rata-rata Hitung (Mean) Data Tunggal Sampel Data Berkelompok Populasi Dengan Koding

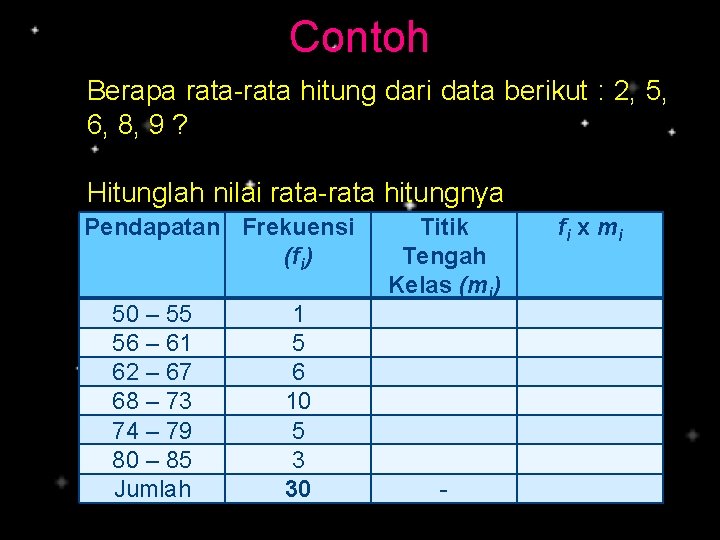
Contoh Berapa rata-rata hitung dari data berikut : 2, 5, 6, 8, 9 ? Hitunglah nilai rata-rata hitungnya Pendapatan Frekuensi (fi) 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah 1 5 6 10 5 3 30 Titik Tengah Kelas (mi) - fi x m i

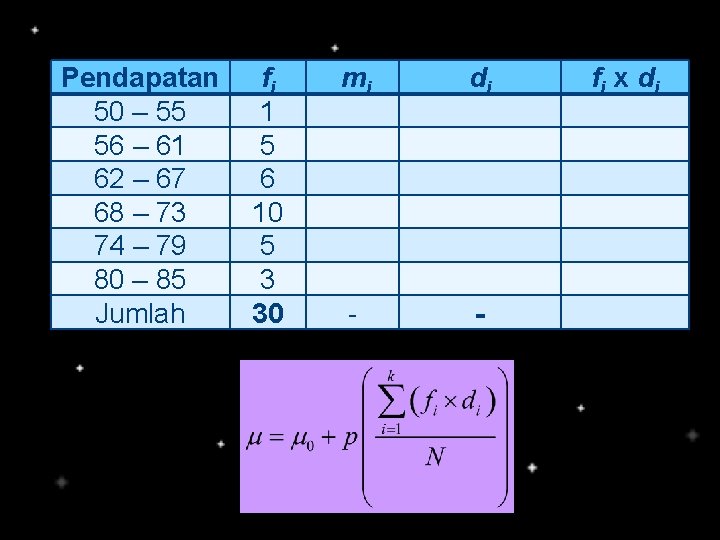
Pendapatan 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah fi 1 5 6 10 5 3 30 mi di - - fi x d i

Rata-rata Ukur/Geometrik (G) Dua data berurutan nilainya tetap atau hampir tetap Misalnya: rata-rata tingkat pertambahan pinjaman setiap bulan di kantor pegadaian, rata-rata pertumbuhan sambungan telepon setiap bulannya. Data Tunggal Bilangan bernilai besar Data Berkelompok

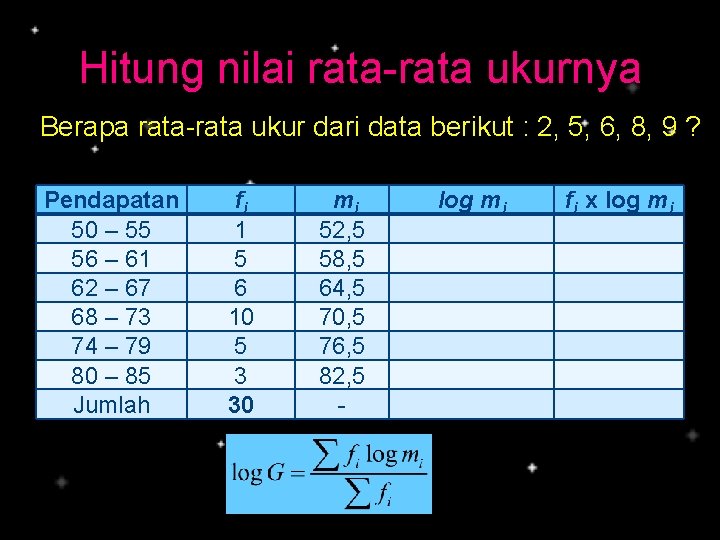
Hitung nilai rata-rata ukurnya Berapa rata-rata ukur dari data berikut : 2, 5, 6, 8, 9 ? Pendapatan 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah fi 1 5 6 10 5 3 30 mi 52, 5 58, 5 64, 5 70, 5 76, 5 82, 5 - log mi fi x log mi

Rata-rata Harmonik untuk merata-ratakan kecepatan beberapa jarak tempuh atau mencari harga rata-rata suatu komoditi tertentu. Data Tunggal Data Berkelompok Berapa rata-rata harmonik dari data berikut : 2, 5, 6, 8, 9 ? Pendapatan fi mi fi /mi 50 – 55 1 52, 5 56 – 61 5 58, 5 62 – 67 6 64, 5 68 – 73 10 70, 5 74 – 79 5 76, 5 80 – 85 3 82, 5 Jumlah 30 -

Modus • Modus: ukuran untuk data yang paling sering muncul/sering terjadi. • Data kualitatif : modus sering dipakai sebagai pengganti rata-rata. • Data kuantitatif, modus diperoleh dengan menentukan frekuensi terbesar dari keseluruhan data. • Satu modus (unimodal), dua modus (bimodal), lebih dari dua (multimodal).

Modus Berapa modus dari data berikut : 2, 3, 5, 3, 6, 9, 3, 9, 5, 6, 5, 1, 5 ? Data Berkelompok Modus ? Kelas ke 1 2 3 4 5 6 Pendapatan 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah fi 1 5 6 10 5 3 30

Median, Kuartil, Desil, Presentil • Median membagi data menjadi 2 bagian setelah data diurutkan (dari kecil ke besar) • Kuartil membagi data menjadi 4 bagian setelah data diurutkan • Desil membagi data menjadi 10 bagian setelah data diurutkan • Presentil membagi data menjadi 100 bagian setelah diurutkan

Median, Kuartil, Desil, Presentil Data Tunggal Median Kuartil Desil Presentil Data Berkelompok

• Tentukan median dari data 2, 6, 8, 5, 4, 9, 12. • Diberikan data 12, 7, 8, 14, 9, 14, 19, 16. Berapa mediannya? • Tentukan kuartil atas dan kuartil bawah dari data berikut 2, 6, 8, 5, 4, 9, dan 12 • Tentukan desil ke-3, ke-7 dan ke-9 dari data berikut 2, 6, 8, 5, 4, 9, 12, 13, 14, dan 15. • Tentukan persentil ke-10, ke-25 dan ke-50 dari data berikut 2, 6, 8, 5, 4, 9, 12, 13, 14, dan 15. Hal 24, 25, 26

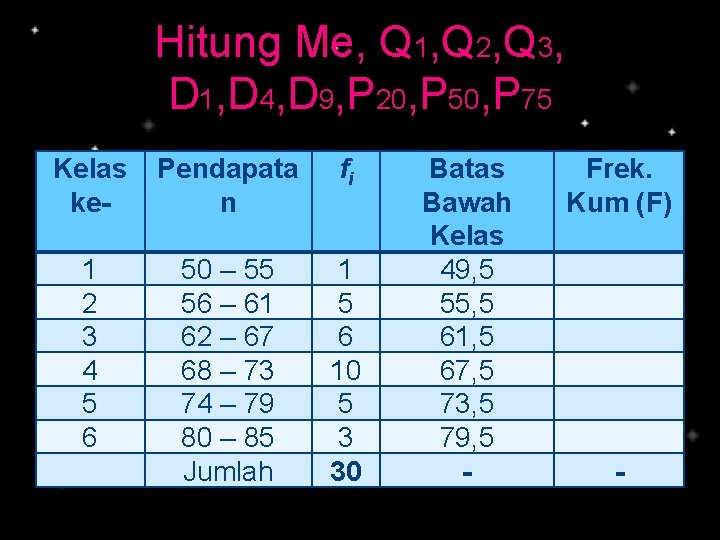
Hitung Me, Q 1, Q 2, Q 3, D 1, D 4, D 9, P 20, P 50, P 75 Kelas ke- Pendapata n fi 1 2 3 4 5 6 50 – 55 56 – 61 62 – 67 68 – 73 74 – 79 80 – 85 Jumlah 1 5 6 10 5 3 30 Batas Bawah Kelas 49, 5 55, 5 61, 5 67, 5 73, 5 79, 5 - Frek. Kum (F) -

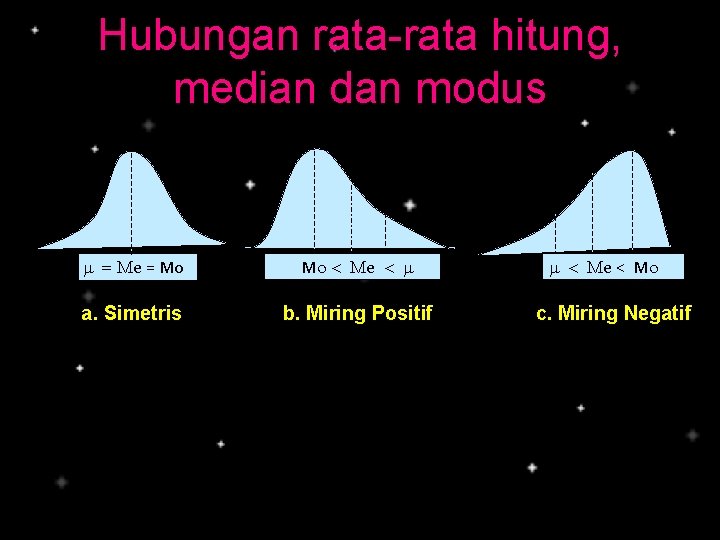
Hubungan rata-rata hitung, median dan modus m = Me = Mo Mo < Me < m a. Simetris b. Miring Positif m < Me < Mo c. Miring Negatif