An Untangled Introduction to Knot Theory Ana Nora









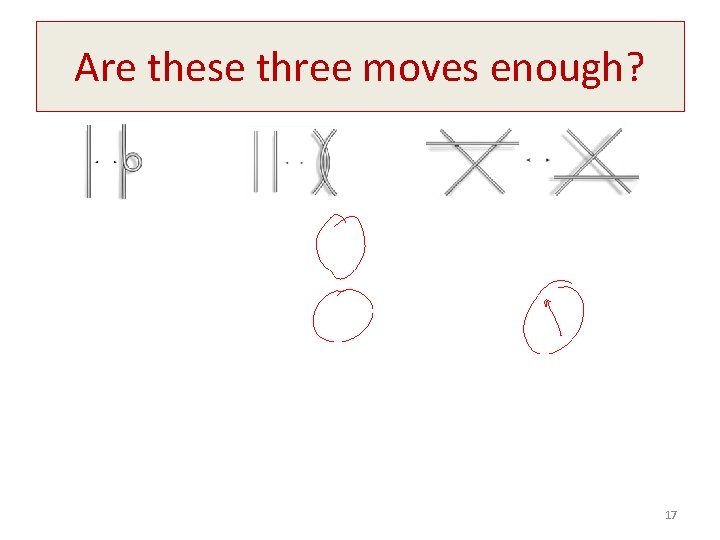
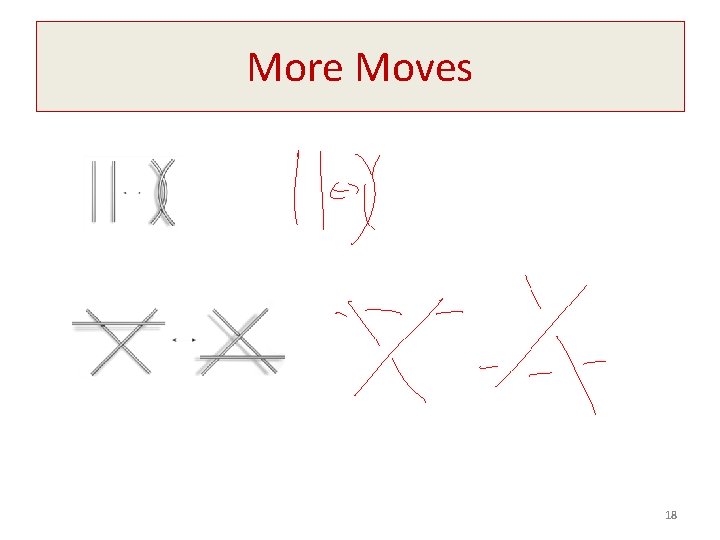

















- Slides: 39

An Untangled Introduction to Knot Theory Ana Nora Evans University of Virginia Mathematics 12 February 2010

Why study knots? • Used in – Biology – Chemistry – Physics – Graph Theory – …. . Rule Asia 2

Gordian Knot “… Seeing Gordius, therefore, the people made him king. In gratitude, Gordius dedicated his ox cart to Zeus, tying it up with a highly intricate knot - - the Gordian knot. Another oracle -or maybe the same one, the legend is not specific, but oracles are plentiful in Greek mythology -- foretold that the person who untied the knot would rule all of Asia. ” From “Untying the Gordian Knot” by Keith Devlin (www. maa. org/devlin_9_01. html) 3

Problem Solved!!! Alexander cuts the Gordian Knot, by Jean-Simon Berthélemy 4

More importantly • It’s fun • Interesting • Hot area of research The Knot Book by Colin C. Adams An Introduction to Knot Theory by W. B. Raymond Lickorish 5

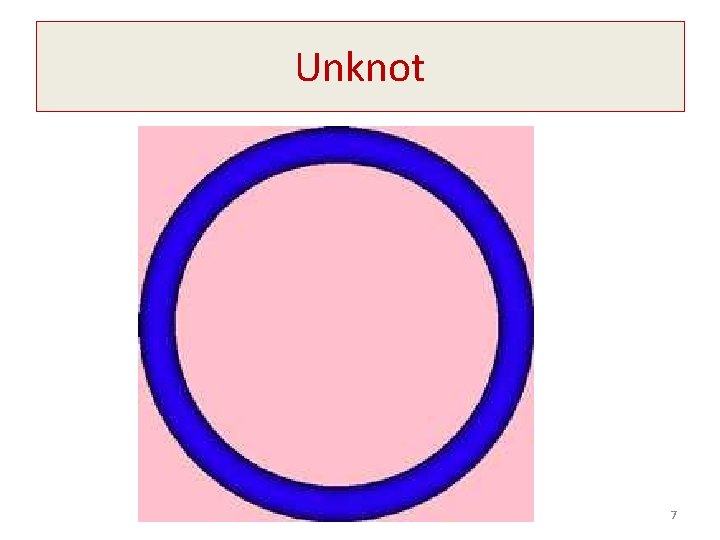
Knot Definition A knot is an embedding of S 1 in R 3. 1. Take a piece a string. 2. Tie a knot in it. 3. Now glue the ends of the string together to form a knotted loop. (see Colin Adams – The Knot Book) 6

Unknot 7

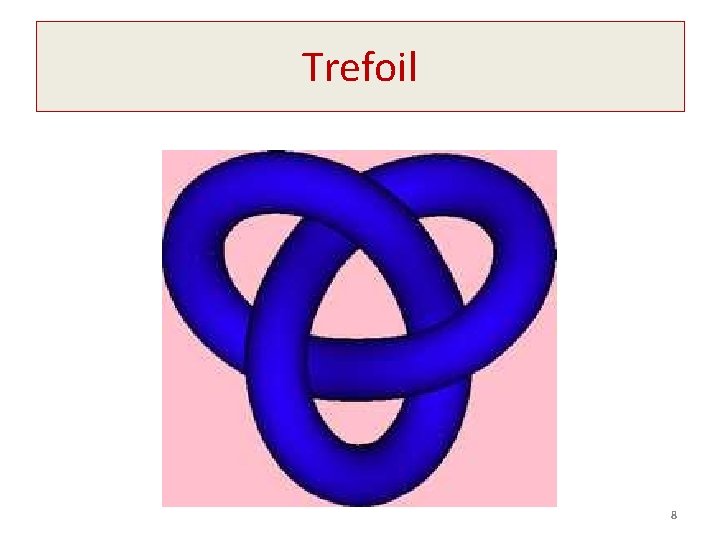
Trefoil 8

Figure 8 9

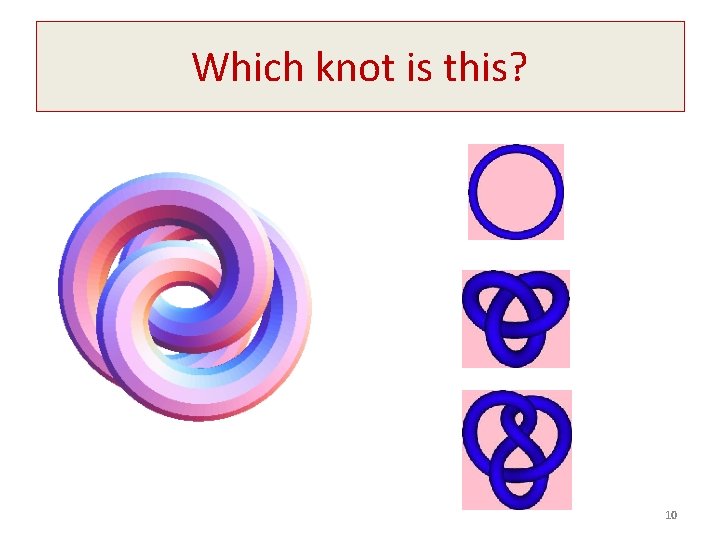
Which knot is this? 10

Planar Diagrams 11

Examples 12

Knot equivalence Two knots are equivalent if there exists an isotopy of R 3 taking one knot to the other. Two knots are equivalent if you can get one from the other by deforming the string without cutting it. 13

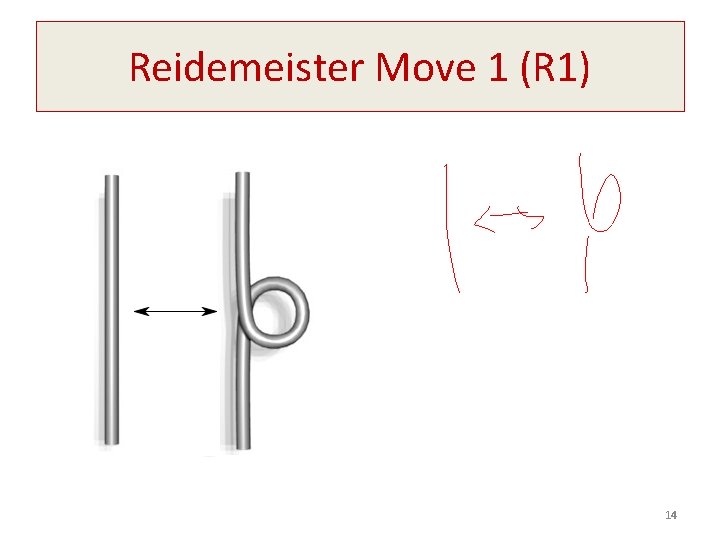
Reidemeister Move 1 (R 1) 14

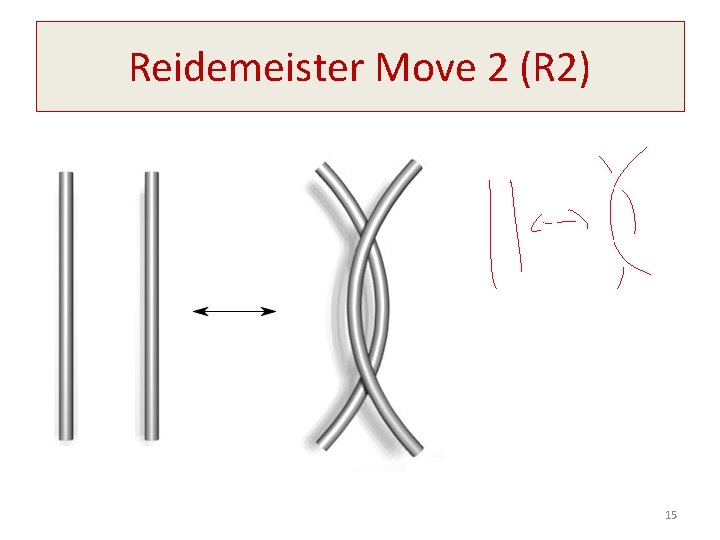
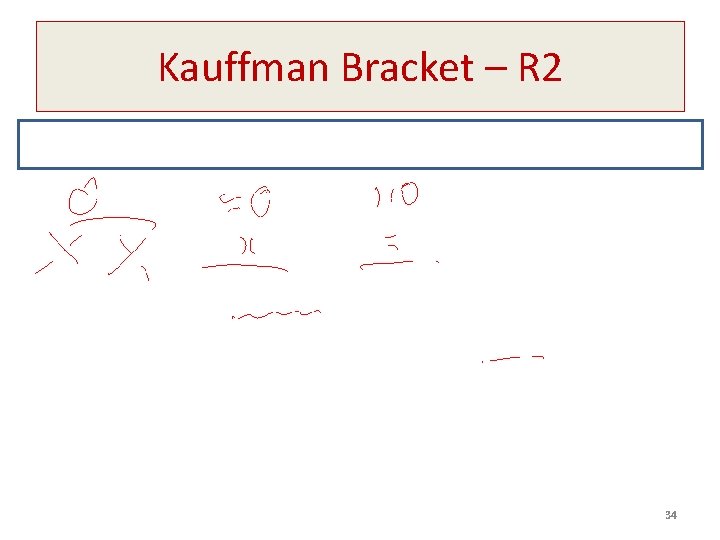
Reidemeister Move 2 (R 2) 15

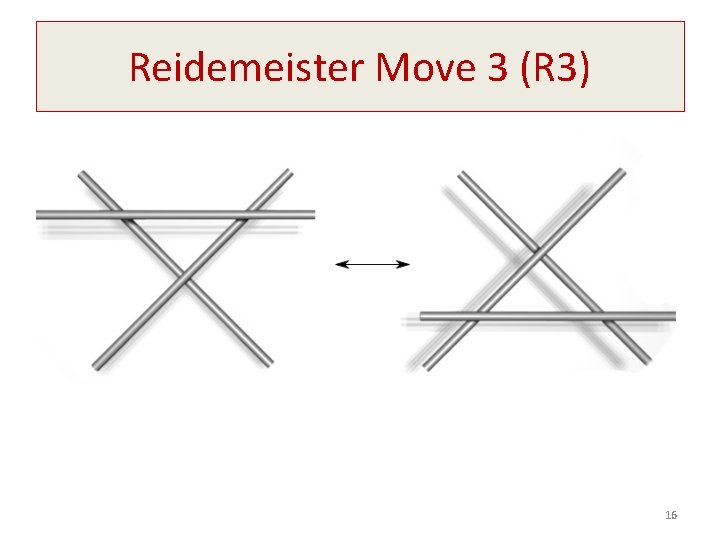
Reidemeister Move 3 (R 3) 16
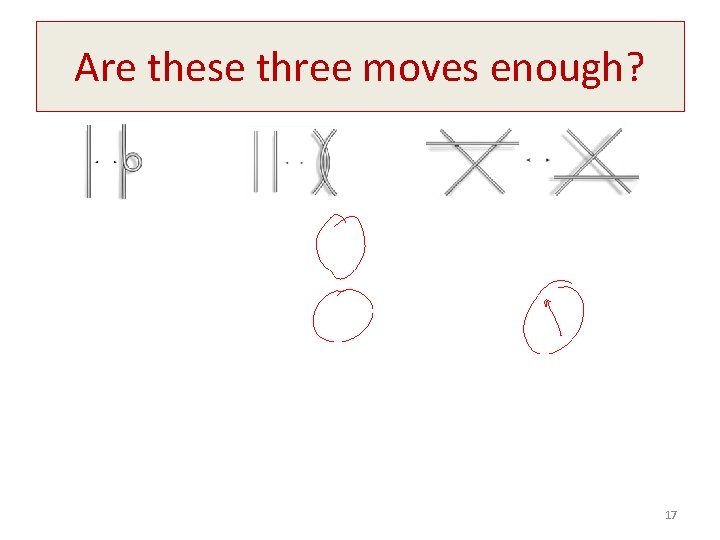
Are these three moves enough? 17
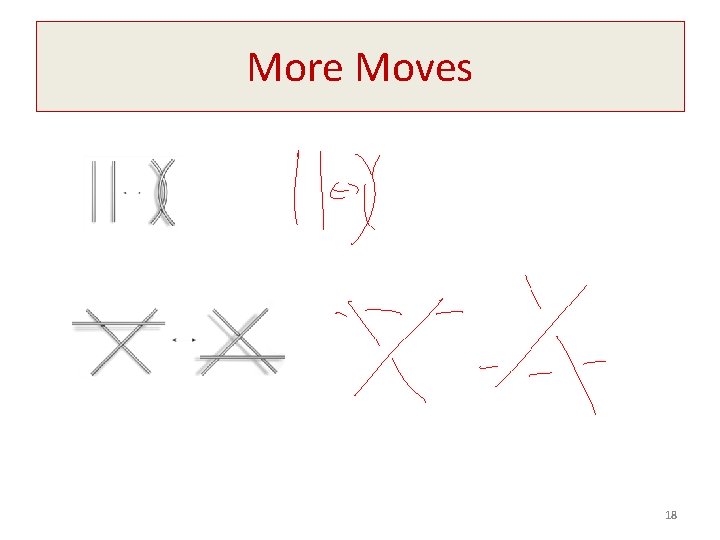
More Moves 18

Which knot is this? 19

Knot Invariants • A knot invariant is a mathematical object associated to a knot – two equivalent knots have the same invariant • Examples – Crossing number – Unknotting number 20

James Waddell Alexander II “Topological invariants of knots and links” In Transactions of the American Mathematical Society (1928) 21

John Conway “An enumeration of knots and links, and some of their algebraic properties” In Computational Problems in Abstract Algebra, 1967 22

Oriented Knots Positive crossing Negative crossing 23

Conway’s Skein Relation 24

Example - Trefoil 25

Example – Hopf Link 26

Example – Unlink 27

Example – Unlink 28

Back to Trefoil 29

Vaughan Jones Fields Medal in 1990 “A polynomial invariant for knots via von Neumann algebras. ” In Bull. Amer. Math. Soc. (N. S. ) Volume 12, Number 1 (1985), 30

Kauffman Bracket 31

Kauffman Bracket - example 32

Jones Polynomial 33

Kauffman Bracket – R 2 34

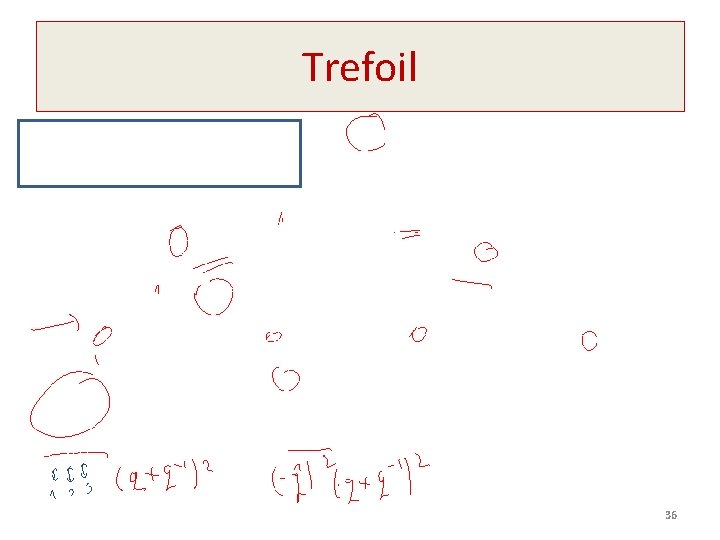
Jones Polynomial – R 2 35

Trefoil 36

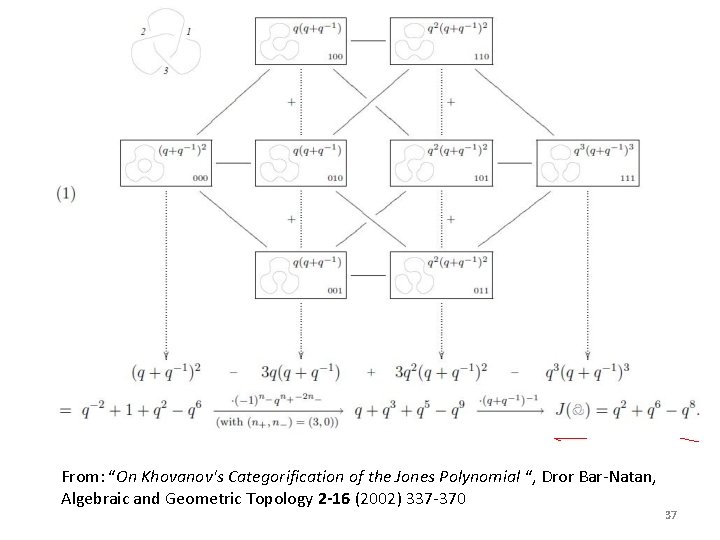
From: “On Khovanov's Categorification of the Jones Polynomial “, Dror Bar-Natan, Algebraic and Geometric Topology 2 -16 (2002) 337 -370 37

Open Question Is there a nontrivial knot with Jones polynomial equal to that of the unknot? It is known that there are nontrivial links with Jones polynomial equal to that of the corresponding unlinks by the work of Morwen Thistlethwaite. 38

Thank you! The talk is available at: http: //www. cs. virginia. edu/nora 39