An Unstructured Grid Finite Volume ThreeDimensional Primitive Equations

An Unstructured Grid, Finite. Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries CHANGSHENG CHEN, HEDONG LIU, And ROBERT C. BEARDSLEY Summary by Charles Seaton, all formulae and figures taken from paper unless otherwise specified

Primitive equations Momentum (u component) Momentum (v component) density continuity Advection of temperature Advection of salinity Density as a function of S and T

Eddy viscosity • Mellor and Yamada 2. 5 turbulence closure scheme Turbulent kinetic energy (TKE) Vertical shear – source for TKE Density (in)stability – source or sink for TKE dissipation – sink for TKE Law of the Wall (E? ) Distance from bed and surface

Eddy viscosity (continued) Stability functions Function of density, TKE and length scale

Boundary conditions Surface boundary for u and v is a function of wind shear Surface boundary condition for w Bottom boundary for u and v is a function of bottom stress Bottom boundary condition for w is a function of bathymetry Temperature has surface heat flux and shortwave radiation sources Salinity has surface precipitation and evaporation Solid horizontal boundaries have 0 velocity and S and T advection normal to the boundary (from manual)

Vertical grid Sigma coordinates (level depths normalized as a fraction of total depth (bathymetry + free surface height) Horizontal diffusion term (horizontal diffusion is restricted to single layer) Sigma layers can be uniform or parabolic

2 D depth averaged equations • Solution for sea surface elevation is determined using depth averaged velocities • Other variables (u, v, w, S, T, etc) are solved in 3 D using the sea surface elevation from the 2 D calculations • “mode splitting” 2 D (“external”) and 3 D (“internal”) modes are calculated on different timesteps 2 D continuity equation

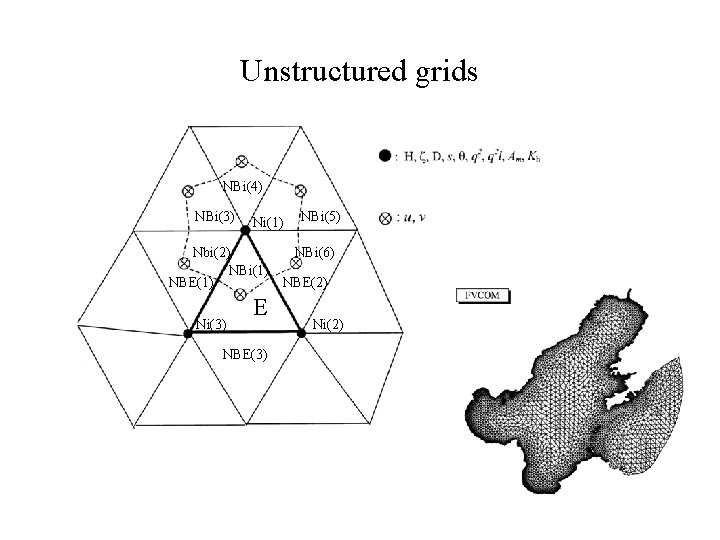
Unstructured grids NBi(4) NBi(3) Ni(1) Nbi(2) NBi(1) NBE(1) Ni(3) E NBE(3) NBi(5) NBi(6) NBE(2) Ni(2)

2 D External mode Integrated continuity equation • Numerically integrated using modified 4 th order Runge-Kutta • Accuracy is 2 nd order, as formulation sets final weights of steps 1 and 2 to 0 • Depth averaged velocity and surface elevation are calculated simultaneously for each sub-step

Standard 4 th order Runge-Kutta From http: //www. physics. orst. edu/~rubin/nacphy/Com. Phys/DIFFEQ/mydif 2/node 6. html Modified 4 th order Runge-Kutta N+1 incorporates initial value and 3 rd estimate

2 D Numerical method P 2 m+1 P 2 m-1 p 2 m k = 1: 4 = (1/4, 1/3, 1/2, 1) Figure not from paper

3 D Numerical method 1 st order upwind advection scheme (other schemes available) 1 level momentum function All the complexity mid-level velocity Next timestep is a function of mid-level velocities Creates a tri-diagonal matrix

Merging the internal and external modes Vertical velocity is calculated to merge results of 2 D and 3 D modes Vertically integrated form Valid if: Distribute error in u and v throughout water column before calculating w (Functions from manual)

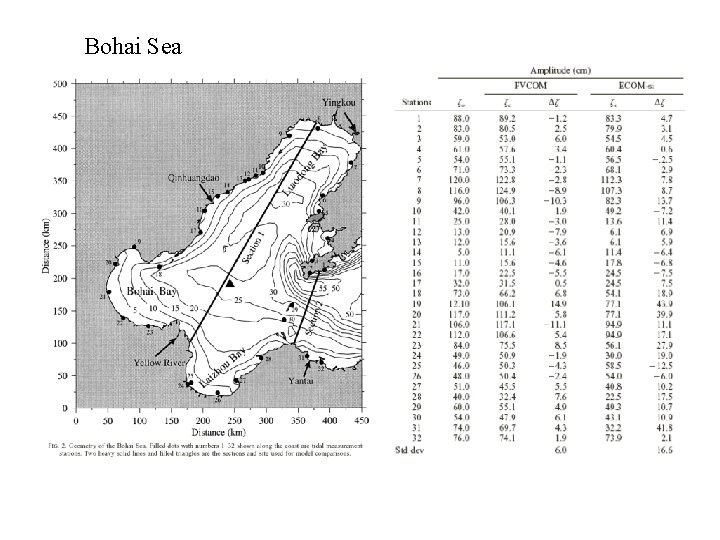
Bohai Sea

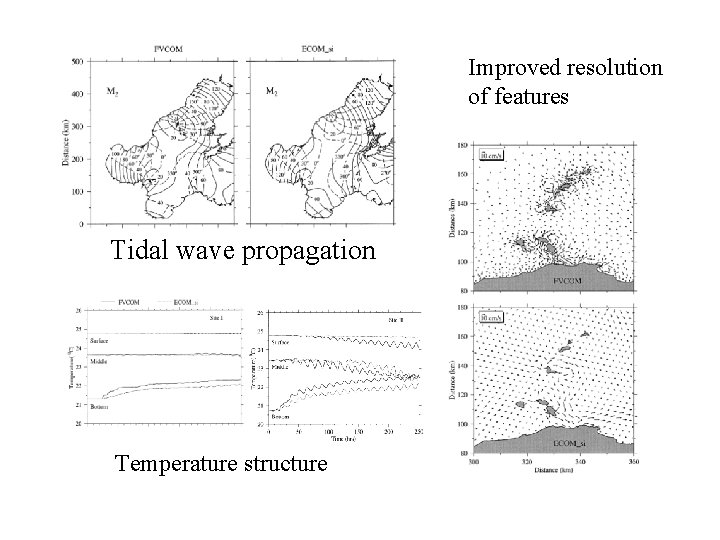
Improved resolution of features Tidal wave propagation Temperature structure

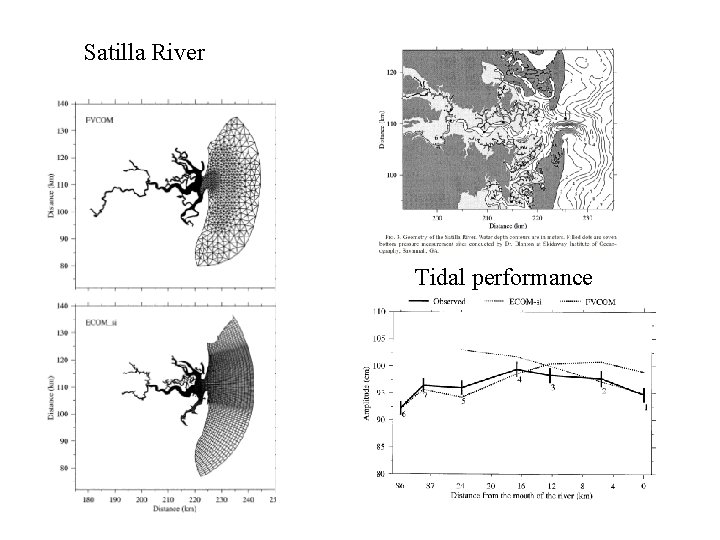
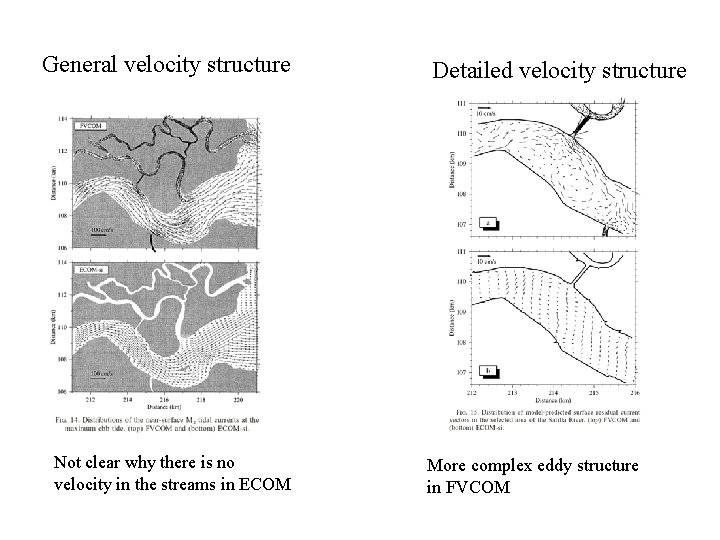
Satilla River Tidal performance

General velocity structure Not clear why there is no velocity in the streams in ECOM Detailed velocity structure More complex eddy structure in FVCOM