An Underwater Acoustic Telemetry Modem for EcoSensing Ronald

An Underwater Acoustic Telemetry Modem for Eco-Sensing* Ronald A. Iltis, Ryan Kastner, and Hua Lee Daniel Doonan, Tricia Fu, Rachael Moore and Maurice Chin Department of Electrical and Computer Engineering University of California, Santa Barbara, CA 93106 -9560 {iltis, kastner, lee}@ece. ucsb. edu *This work was supported in part by the W. M. Keck Foundation and UCSB Marine Sciences Institute. 1

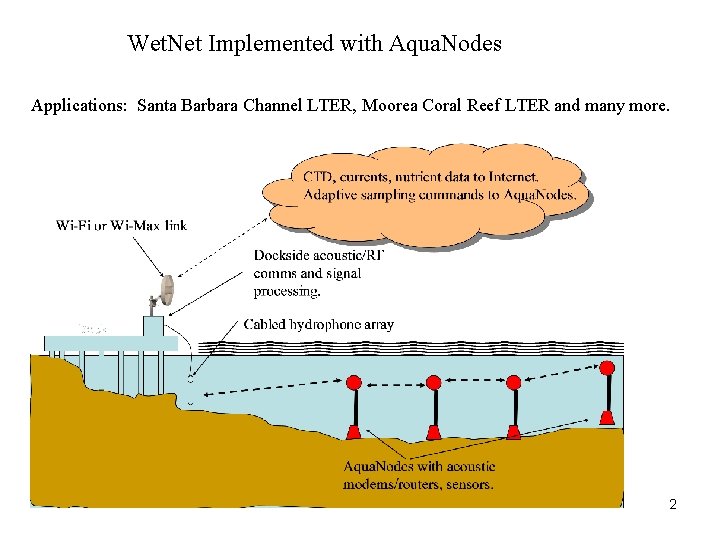
Wet. Net Implemented with Aqua. Nodes Applications: Santa Barbara Channel LTER, Moorea Coral Reef LTER and many more. 2

Modem Alternatives • Commercial modems: (Benthos, Linkquest…) – Too expensive, power hungry for Eco-Sensing. Proprietary algorithms, hardware. – M-FSK (Scussel, Rice 97, Proakis 00) does use frequency diversity, but requires coding to erase/correct fades. • Navy modems: – Need open architecture for international LTER community – precludes military products. • Direct-sequence, QPSK, QAM, coherent OFDM – Great deal of work on DS, QPSK for underwater comms. But equalization, channel estimation are difficult. (Stojanovic 97, Freitag, Stojanovic 2001, 2003. ) • Micro. Modem: – Best available solution for Wet. Net. FSK/Freq. Hopping relies on coding to correct bad hops. – But can we do better? Less power? Wider bandwidth for lower uncoded symbol error rate (SER)? • Aqua. Node modem: Uses Walsh/m-sequence signalling, matching pursuits channel estimation. – – – Uses per-symbol frequency diversity. Motivated by 802. 15. 4 (Zigbee), 802. 11 b m-ary quasi-orthogonal waveforms. Achieves 133 bps data rate without need for equalization, accurate carrier phase tracking. Battery life in months for reasonable transmit duty cycles. Matching Pursuits only assumes channel constant over 22 msec. Far superior to FSK in slow fading (Doppler spread <. 1 Hz) scenario using Kalman filter channel tracking. 3

Multipath/Doppler Spread References • Long range shallow water multipath spread ~100 msec. (Kilfoyle and Baggeroer 00) • 120 msec. spread at 48 nm, 5 msec. at 2 nm shallow water (Stojanovic et. al. 94) • Significant delay spread ~10 msec. 2 -6 meter depth, 400 -500 m range. (Freitag et. al. JOE 01) • 2. 5 msec multipath spread, . 5 Hz Doppler spread at 3 km (6 to 30 m depth) in Baltic. (Sozer et. al. 99) • . 67 msec. multipath spread for two-ray channel (Benson et. al. 00) • Conjecture: A broad class of short range (< 500 m) shallow water channels exists with temporal multipath spread ~10 msec. , Doppler spread < 1 Hz. 4

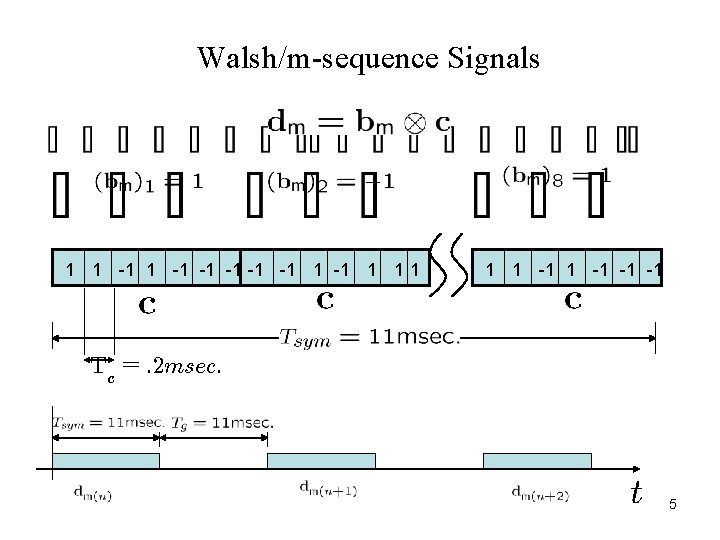
Walsh/m-sequence Signals 1 1 -1 -1 -1 1 1 -1 -1 -1 Tc = : 2 msec: 5

Motivation for Walsh/m-sequence Waveforms • Wideband (5 k. Hz) yields frequency diversity. • 3 bits/symbol yields 10 log 3 = 4. 8 d. B coding gain relative to binary FSK. • Does not require accurate phase tracking for detection (c. f. QPSK, QAM. ) • Time-guard band eliminates need for equalization. • Sparse channel estimation easily implemented via Matching Pursuits. 6

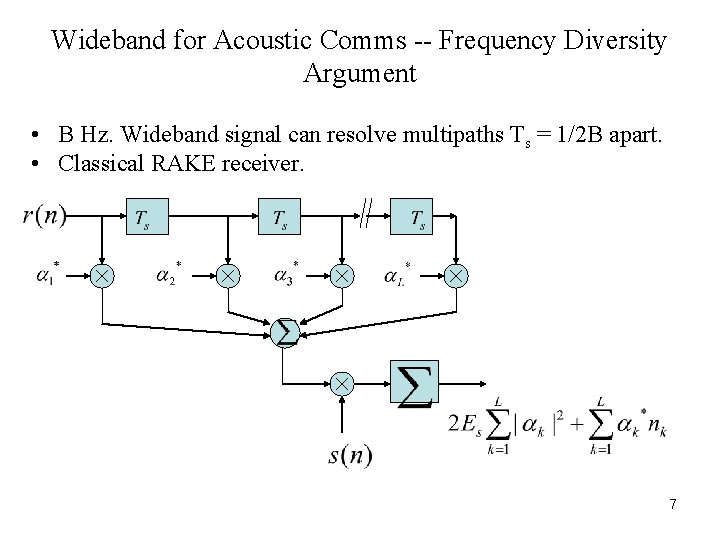
Wideband for Acoustic Comms -- Frequency Diversity Argument • B Hz. Wideband signal can resolve multipaths Ts = 1/2 B apart. • Classical RAKE receiver. 7

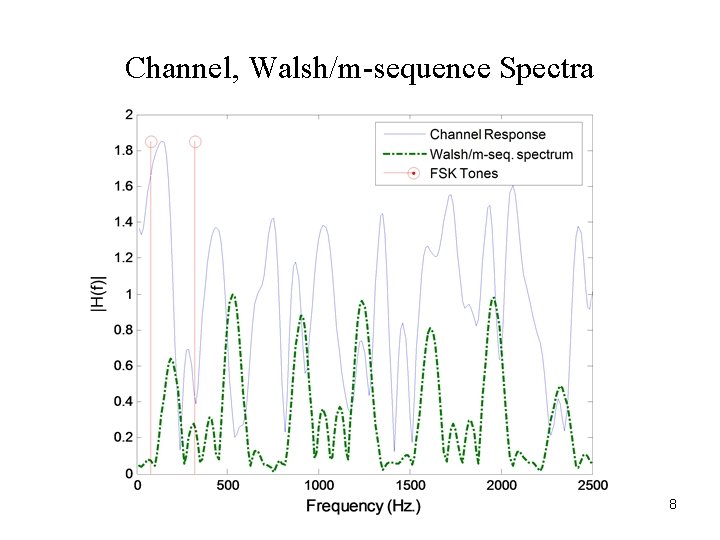
Channel, Walsh/m-sequence Spectra 8

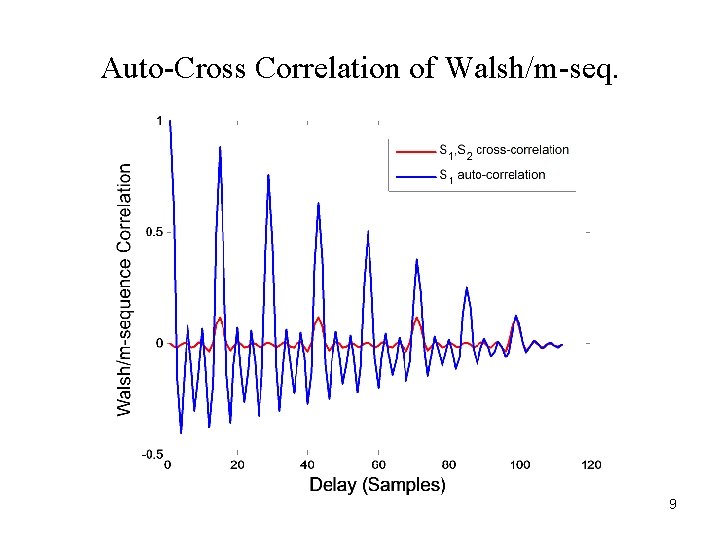
Auto-Cross Correlation of Walsh/m-seq. 9

Un-coded SER Improvement with Diversity FSK in Rayleigh Fading P 2 = 1 2+ Eb µ Diversity¶inµi. i. d. Rayleigh ¶ Binary µ Orthogonal¶ with L-degree X Fading. Ideal RAKE – zero cross-correlation. ¡ ¡ (J. G. Proakis 7. 4. 15) L L 1 1 ¹ P 2 = N 0 ¡ L 1+k 2 k 1+¹ 2 k k =0 ¹= fj Eb LN 0 2+ Eb LN 0 Union Bound Pe < (Nw ¡ 1)P 2 j g Law of Large P Numbers Interpretation – Normalized Channel Energy 2 Es L k=1 E ®k 2 = 1 L j j ! fj j g ®k 2 2 Es LE ®k 2 = 2 Es 10

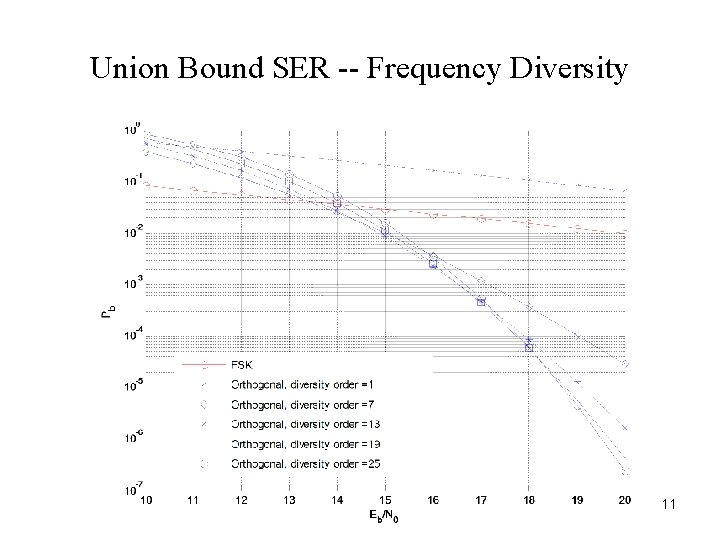
Union Bound SER -- Frequency Diversity 11

Received Signal Model X Transmitted Walsh/m-sequence ¡ sm(n) (t) = Received signal r(t) = Nw Lpn 1 X N® (dm(n) )i g(t ¡ i. Tc ) i=0 ®p (n)sm(n) (t ¡ ¿p (n)) + n(t) p=1 X Nyquist-sampled¡equivalent vector signal r(n) ¼ Ns 1 fl sm(n) (l) + n(n) = Sm(n) f + n(n) l=0 12

Matching Pursuits Channel Estimation 2 Tsym • Conventional LS estimate is “noisy” for sparse channels (Nf << components of f are nonzero. ) • Assume “minimum underspread” channel. Coefficients f are constant only during one symbol+time guard interval (22. 4 msec. ) • Matching Pursuits (Mallat and Zhang, Cotter and Rao 02, Kim and Iltis 04) yields sparse channel estimates and is readily implemented in reconfigurable hardware (Meng et. al. DAC 05. ) r(n) ¼ s(q 2 )f^q + s (q 1 )f^q + s(q. N )f^q f 2 Nf + s(q 3 )f^q 3 1 13

MP Algorithm ¯ • Step 1 –^ Conventionaljj¯¯¯¯LS, jj best ¯¯fit. ¯ fi q 1 = s(i)H r= ¯¯s(i) 2 ; i =¯¯ 1; : : : ; N s ¡ = arg min r s(i)f^ 2 i i j j jj jj = arg max f^ 2 s(i) 2 i i X ¡ detected paths, find q Step k – Cancel previous k-1 k ¡k 1 rk = r s(qi )f^q i i=1 jj jj¯¯ ¯¯ s(i)H rk = s(i) ¯ 2¯ f^i = qk = arg ¡ rk s(i)f^i i=q 1 ; : : : ; qk ¡ 1 j j jj jj = arg max f^i 2 s(i) 2 min i=q 1 ; : : : ; qk ¡ 1 ¯¯ ¯¯ ¯¯ 2 14

½GMHT-MP Algorithm ¾ • Decision on m(n) using Generalized Multiple Hypothesis Test (GMHT) jj jj ¡ ^ = arg min m m min f : ´(f )=Nf r(n) Sm f 2 Numerosity constraint GMHT has complexity Nw binom(Ns, Nf) due to numerosity constraint. For Nf = 12 paths, this requires 35 x 1015 LS channel estimates requiring matrix-vector multiplies! n o MP estimation requires Nw Ns!/(Ns-Nf)! = 1. 7 x 1025 least-squares estimates, but these are scalar quanitities. MP also only requires one matrix-vector multiply jj statistics. jj has the form ¡ GMHT-MP thus when implemented using sufficient ^ = arg min r(n) Sm ^f M P; m 2 m m 15

Sufficient Statistics MP Implementation (A. Brown and Y. Meng, DAC 05) • Step 1: Matrix-vector multiply v 1 = SH r(n); j(look-up table) v 1 2 = arg max i ; Ai; i i v 1 i = Ai; i ¡ = v 1 A(: ; q )f^ q 1 f^q A = SH S j 1 v 2 1 q 1 j j Step k: Does not require further matrix-vector vk 2 multiplies. qk f^q k vk+1 = arg max i i Ai; i ; vk i = Ai; i ¡ = vk A(: ; q )f^ k q k 16

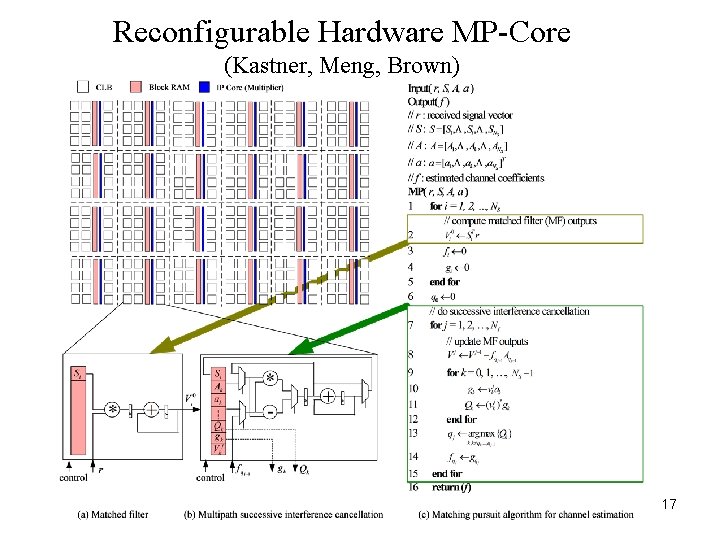
Reconfigurable Hardware MP-Core (Kastner, Meng, Brown) 17

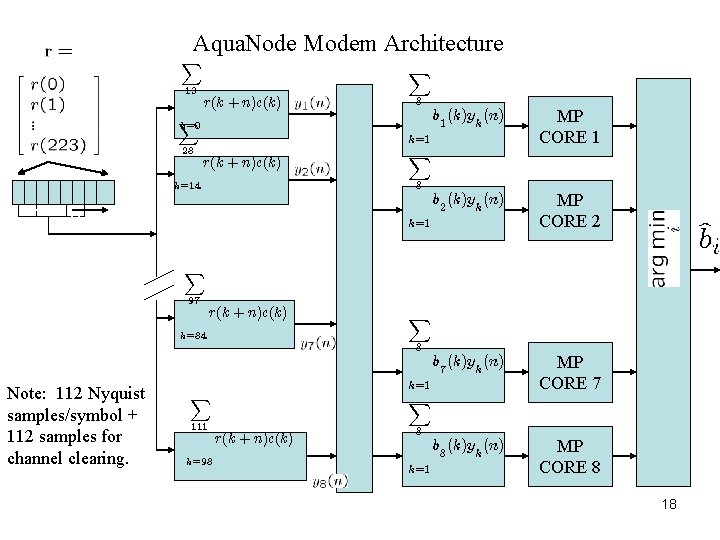
Aqua. Node Modem Architecture X 13 X k =0 r(k + n)c(k) X 8 b 1 (k)yk (n) MP CORE 1 b 2 (k)yk (n) MP CORE 2 b 7 (k)yk (n) MP CORE 7 b 8 (k)yk (n) MP CORE 8 k=1 28 r(k + n)c(k) k =14 X 8 k=1 X 97 r(k + n)c(k) k =84 X 8 Note: 112 Nyquist samples/symbol + 112 samples for channel clearing. X k=1 111 k =98 r(k + n)c(k) X 8 k=1 18

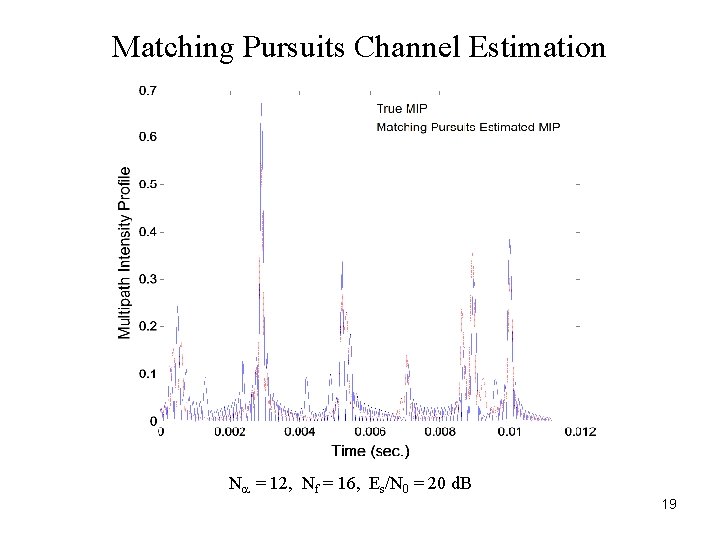
Matching Pursuits Channel Estimation Na = 12, Nf = 16, Es/N 0 = 20 d. B 19

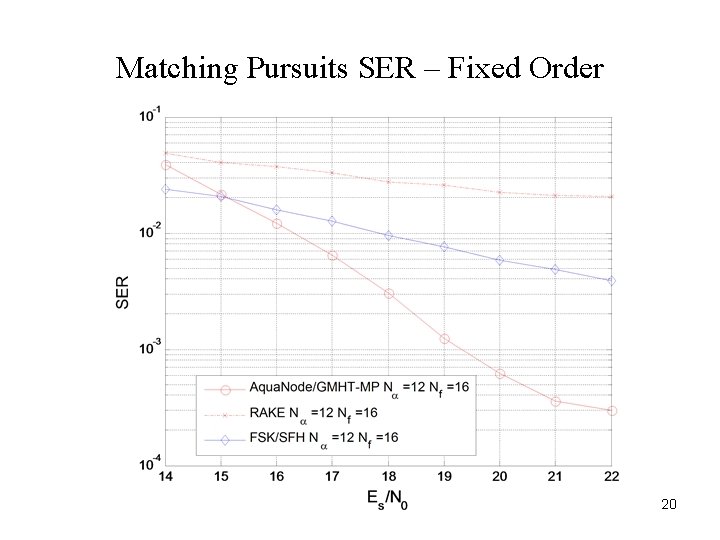
Matching Pursuits SER – Fixed Order 20

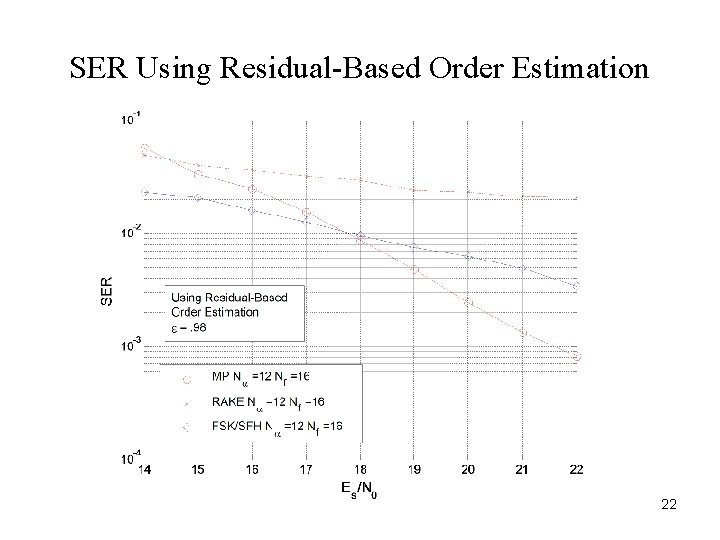
Channel Order Estimation • MDL and AIC yield overparameterized channel estimates. • Modified MDL uses penalty term increasing with SNR and channel order, but requires optimization of penalty weight. • Heuristic algorithm: Stop when decrease in error is below a threshold. ¯¯ ¯¯ ¯¯ ¯^¯ X N ¯¯ ¯¯f ¯¯ ¯¯ 2 ¡ k r(n) s(qi )f^q i i= 1 ¯¯ = k ¯¯¯¯ if X ¯¯ ¯¯ ¡ k+1 s(qi )f^q > ¯ r(n) i=1 i ¯¯ ¯¯ ¯¯ 2 Typical values of b are. 95, . 98. 21

SER Using Residual-Based Order Estimation 22

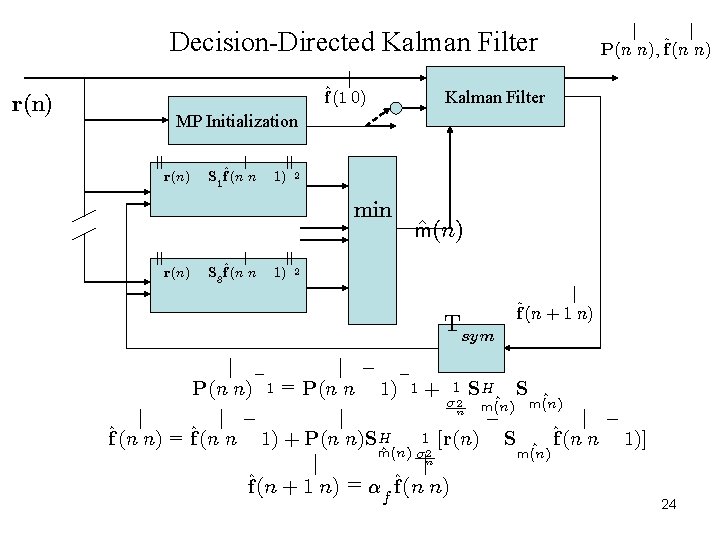
Kalman Filter Channel Estimator • MP only requires channel constant over Tsym = 22. 4 msec. Good solution for large Doppler spreads (>. 1 Hz. ) • For Doppler spreads fd <. 1 Hz, Kalman filter channel estimator is promising. • Use decision-directed KF with process/measurement models jj j ¡ jj ¡ = arg min r(n) ^ m(n) m Sm^ ^f (n n 1) 2 f (n + 1) = ®f f (n) + w(n) f (n) + n(n) r(n) = Sm(n) ^ 23

Decision-Directed Kalman Filter j ^f(1 0) r(n) j j P(n n); ^f (n n) Kalman Filter MP Initialization jj r(n) ¡ jj ^ S 1 f (n n 1) 2 min jj r(n) ¡ ^ m(n) j ¡ jj ^ S 8 f (n n 1) 2 Tsym j ^f (n + 1 n) j ¡ ¡ P(n n) 1 = P(n n 1) 1 + 1 SH S ^ ^ ¾ 2 m(n) n ¡ j j ¡ ^f (n n) = ^f (n n 1) + P(n n)SH 1 [r(n) S ^ ^f (n n 1)] j ¡ j ^ m(n) ¾ 2 jn ^f (n + 1 n) = ® ^f (n n) f m(n) 24

Union Bound Conditional SER Ã • Analytic union bound SER speeds up KF simulations. ! • Pairwise error probability. jj ¡ jj ^f ) 2 1 S 1 f S 2^f ¡ S (f jj 2 ¡ jj P 1; 2 = erfc ¾n 2 ¾n S 1 ^f S 2^f XX SNR decrease due to estimation error 1 Pe < Nw Nw Nw Pi; j i= 1 j = 1 25

Kalman Filter Channel Estimation 26

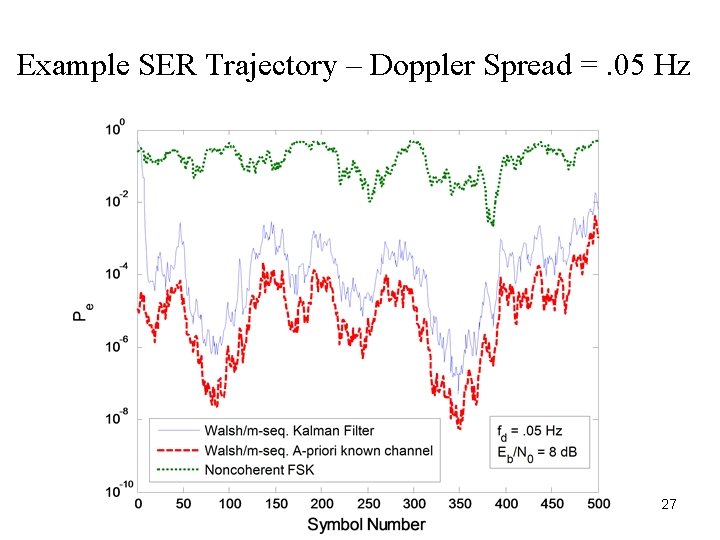
Example SER Trajectory – Doppler Spread =. 05 Hz 27

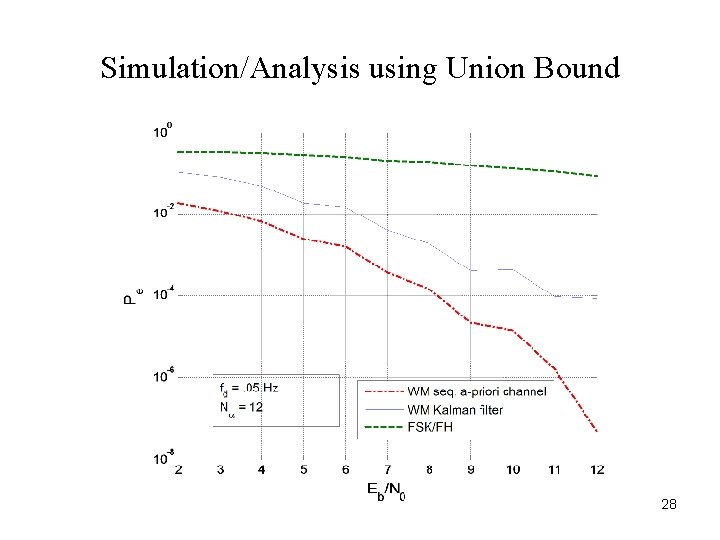
Simulation/Analysis using Union Bound 28

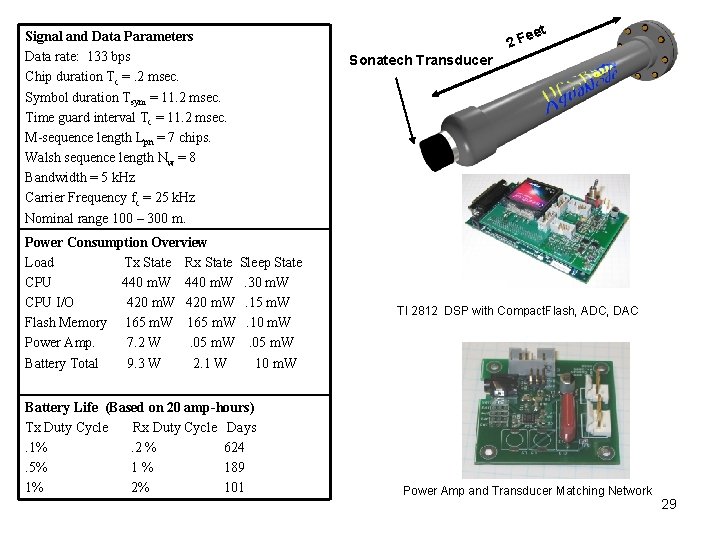
Signal and Data Parameters Data rate: 133 bps Chip duration Tc =. 2 msec. Symbol duration Tsym = 11. 2 msec. Time guard interval Tc = 11. 2 msec. M-sequence length Lpn = 7 chips. Walsh sequence length Nw = 8 Bandwidth = 5 k. Hz Carrier Frequency fc = 25 k. Hz Nominal range 100 – 300 m. Power Consumption Overview Load Tx State Rx State Sleep State CPU 440 m. W. 30 m. W CPU I/O 420 m. W. 15 m. W Flash Memory 165 m. W. 10 m. W Power Amp. 7. 2 W. 05 m. W Battery Total 9. 3 W 2. 1 W 10 m. W Battery Life (Based on 20 amp-hours) Tx Duty Cycle Rx Duty Cycle Days. 1%. 2 % 624. 5% 1% 189 1% 2% 101 t ee 2 F Sonatech Transducer TI 2812 DSP with Compact. Flash, ADC, DAC Power Amp and Transducer Matching Network 29

Conclusions • Walsh/m-sequence signaling exploits frequency diversity and yields lower uncoded SER than FSK. • Matching Pursuits algorithm enforces sparse estimates, implemented in FPGA and DSP. • Modem should be adaptive, using Kalman or MP channel estimation depending on sensed channel variation, velocity. • Can a numerosity-constrained Kalman filter be developed? Better performance for fd >. 1 Hz? • First generation modem implementable in DSP, but second gen. will require DSP +FPGA. 30