An Overview of the Common Core State Standards



































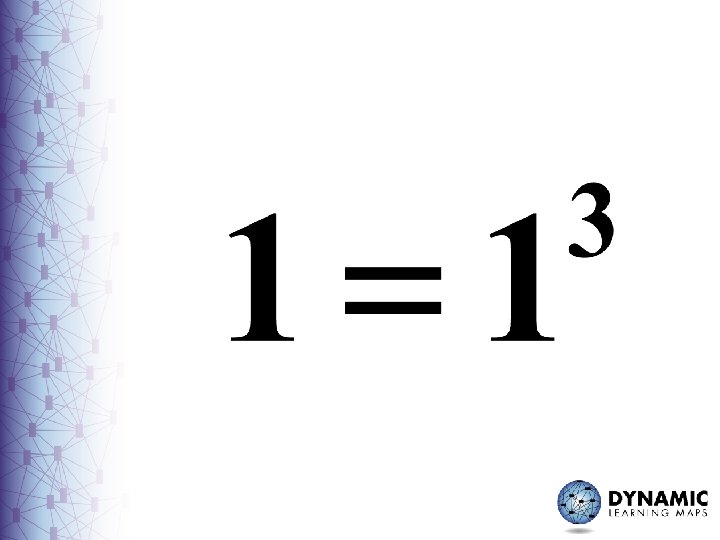










- Slides: 48


An Overview of the Common Core State Standards for Mathematical Practice for use with the Common Core Essential Elements The present publication was developed under grant 84. 373 X 100001 from the U. S. Department of Education, Office of Special Education Programs. The views expressed herein are solely those of the author(s), and no official endorsement by the U. S. Department should be inferred.

8 Standards of Mathematical Practice Standard 1: Make sense of problems and persevere in solving them Standard 2: Reason abstractly and quantitatively Standard 3: Construct viable arguments and critique the reasoning of others Standard 4: Model with mathematics Standard 5: Use appropriate tools strategically Standard 6: Attend to precision Standard 7: Look for and make use of structure Standard 8: Look for and express regularity in repeated reasoning

Grouping the Standards of Mathematical Practice (Mc. Callum, 2011)

Standard 1: Make sense of problems and persevere in solving them

Mathematically proficient students: – explain the meaning of a problem and look for solutions – analyze – make conjectures about the form and meaning of the solution to plan a solution pathway – monitor and evaluate their progress – explain correspondences between equations, verbal descriptions, tables, and graphs or draw diagrams to show relationships or trends. – check their answers to problems using a different methods

Standard 1: What might it look like for a student with significant cognitive disabilities?

“Key Words” as an example of the “suspension of sense making” Key words don’t work!

We tell them—more means add Erin has 46 comic books. She has 18 more comic books than Jason has. How many comic books does Jason have. But is our answer really 64 which is 46 + 18?

Standard 2: Reason abstractly and quantitatively

• Mathematically proficient students: – make sense of quantities and their relationships – bring two complementary abilities to bear on problems involving quantitative relationships: • the ability to decontextualize • the ability to contextualize • Quantitative reasoning entails habits of creating a coherent representation of the problem at hand

Standard 3: Construct viable arguments and critique the reasoning of others

• Mathematically proficient students: – understand use stated assumptions, definitions, and previously established results – make conjectures – analyze situations by breaking them into cases and, can recognize and use counterexamples. – reason inductively about data – compare the effectiveness of two plausible arguments, distinguish correct logic or reasoning from that which is flawed – listen or read the arguments of others, decide whether they make sense

Grouping the Standards of Mathematical Practice (Mc. Callum, 2011)

Standards 2 & 3: What might they look like for a student with significant cognitive disabilities?

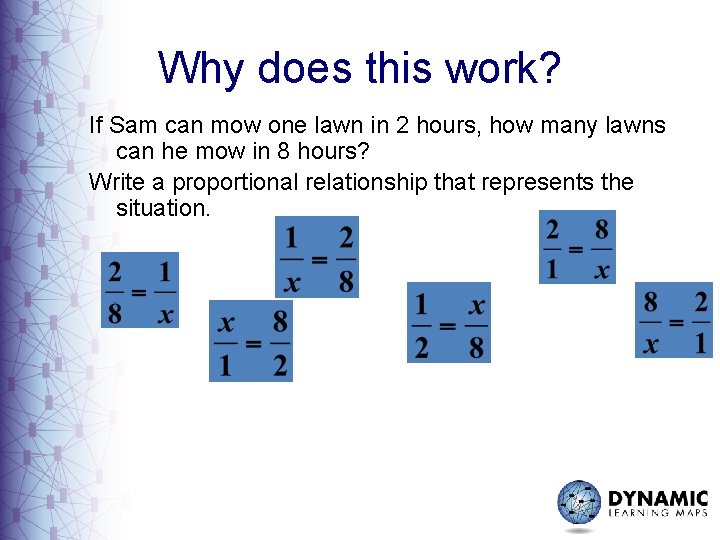
Why does this work? If Sam can mow one lawn in 2 hours, how many lawns can he mow in 8 hours? Write a proportional relationship that represents the situation.

Representational proportions =

Concrete Proportions = X = X =

Standard 4: Model with mathematics

• Mathematically proficient students: – apply the mathematics – identify important quantities in a practical situation and map their relationships – analyze relationships mathematically to draw conclusions – Routinely interpret their mathematical results in the context of the situation

Standard 5: Use appropriate tools strategically

• Mathematically proficient students: – consider the available tools when solving a mathematical problem – are sufficiently familiar with tools appropriate for their grade or course – know that technology can enable them to visualize the results – identify relevant external mathematical resources, and use them to pose or solve problems – are able to use technological tools to explore and deepen their understanding of concepts

Grouping the Standards of Mathematical Practice (Mc. Callum, 2011)

Standards 4 & 5: What might they look like for a student with significant cognitive disabilities?

Your New Car! You are buying a new car that is on sale for $27, 000. This is 80% of the Original cost of the car. What was the Original cost of the car?

Using Hundreds Board to Solve Relatively Difficult Problems

Using Hundreds Board to Solve Relatively Difficult Problems Or igi na l. C os t: 10 0%

Using Hundreds Board to Solve Relatively Difficult Problems

Using Hundreds Board to Solve Relatively Difficult Problems Or igi na l. C 27, 000 os t: 1 Sale Cost 00%

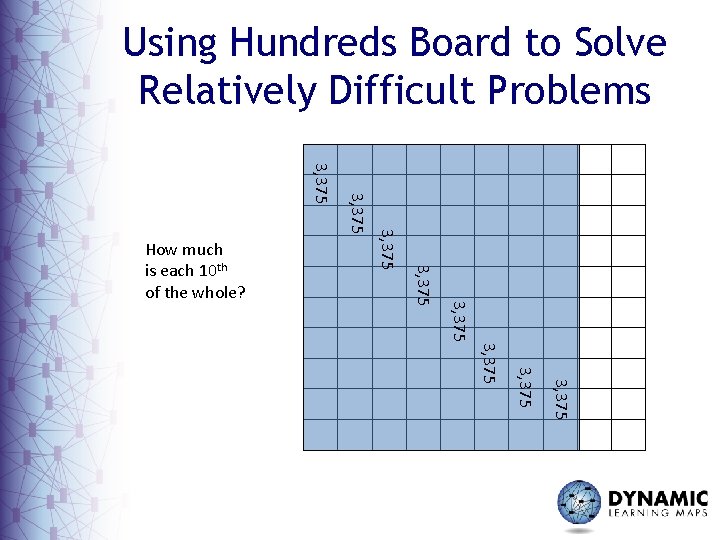
Using Hundreds Board to Solve Relatively Difficult Problems How much is each 10 th of the whole? 27, 000

Using Hundreds Board to Solve Relatively Difficult Problems 3, 375 3, 375 How much is each 10 th of the whole? 3, 375

Using Hundreds Board to Solve Relatively Difficult Problems 3, 375 x 10 Original Cost: 100%

Standard 6: Attend to precision

• Mathematically proficient students: – try to communicate precisely to others – use clear definitions in discussion with others and in their own reasoning – state the meaning of the symbols they choose – are careful about specifying units of measure – calculate accurately and efficiently

Standard 6: What might they look like for a student with significant cognitive disabilities?

We also use the word “same” when it doesn’t really apply.

Are these the same? 4+4 = 7+1
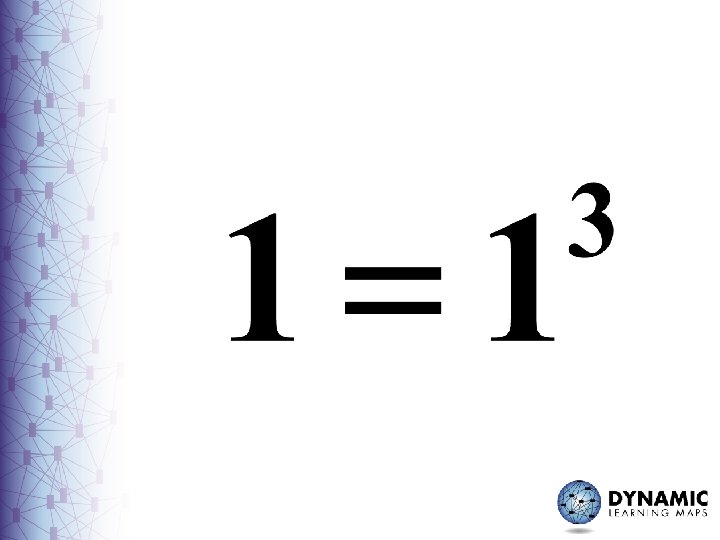

Are these the same?

Standard 7: Look for and make use of structure

• Mathematically proficient students: – look closely to discern a pattern or structure – recognize the significance of an existing line in a geometric figure and can use the strategy of drawing an auxiliary line for solving problems. – can step back for an overview and shift perspective – can see complicated things as single objects or as being composed of several objects

Standard 8: Look for and express regularity in repeated reasoning

• Mathematically proficient students: – notice if calculations are repeated, and look both for general methods and for shortcuts – maintain oversight of the process, while attending to the details – continually evaluate the reasonableness of their intermediate results

Grouping the Standards of Mathematical Practice (Mc. Callum, 2011)

Standards 7 & 8: What might they look like for a student with significant cognitive disabilities?

Multiplication 6 * 7= ?

Multiplication 6 * 7 = 6 (5) + 6 (2) = 42 6 * 7 = 42 or 30 + 12 = 42 -----OR-----6 * 7 = 6 (6) + 6 (1) = 42 6*7 = 42 or 36 + 6 = 42

THANK YOU! For more information, please go to: www. dynamiclearningmaps. us
 Common core state standards pa
Common core state standards pa Connecticut common core state standards
Connecticut common core state standards Common core state standards missouri
Common core state standards missouri Common core standards arkansas
Common core standards arkansas Georgia common core standards
Georgia common core standards Bilingual common core standards
Bilingual common core standards Unpacking the standards template
Unpacking the standards template Common core reading
Common core reading Common core standards kentucky
Common core standards kentucky Common career technical core
Common career technical core Overview of the current state of technology
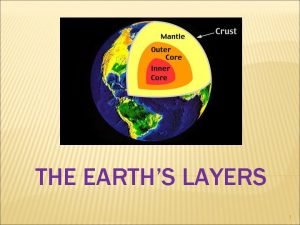
Overview of the current state of technology The brittle, rocky outer layer of earth
The brittle, rocky outer layer of earth The strong lower part of the mantle
The strong lower part of the mantle Which layer is the least dense
Which layer is the least dense Purpose of paradox
Purpose of paradox 7 domains of national core standards
7 domains of national core standards Danielson framework summary
Danielson framework summary Idaho core teaching standards
Idaho core teaching standards Achieve the core priority standards
Achieve the core priority standards Utah common core math
Utah common core math Factors necessary for service standards are
Factors necessary for service standards are Essential elements standards
Essential elements standards Ela regents part 3 rubric
Ela regents part 3 rubric Nys common core math
Nys common core math Common core essential elements michigan
Common core essential elements michigan Common core sheets.com
Common core sheets.com Common core formative assessments
Common core formative assessments 4th grade math jeopardy common core
4th grade math jeopardy common core Common core lattice multiplication
Common core lattice multiplication Nys common core mathematics
Nys common core mathematics Lesson 9 awkward who chose the number 360
Lesson 9 awkward who chose the number 360 Nys common core mathematics curriculum
Nys common core mathematics curriculum Common core ela assessments
Common core ela assessments Common induction standards
Common induction standards Common education data standards
Common education data standards Lcm for 4 and 12
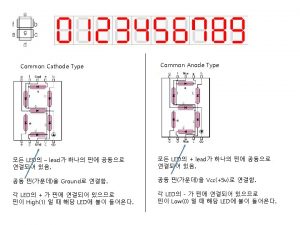
Lcm for 4 and 12 Common anode and common cathode
Common anode and common cathode Factor tree for 56
Factor tree for 56 Lowest common factor
Lowest common factor Lcm of 48 and 60
Lcm of 48 and 60 Highest common factors and lowest common multiples
Highest common factors and lowest common multiples What are the rules in the selection of delta?
What are the rules in the selection of delta? Properties of outer core
Properties of outer core Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Thang điểm glasgow
Thang điểm glasgow